Dynamic Simulation Model of Channel Leakage Based on Multiple Regression
Abstract
:1. Introduction
2. Materials and Methods
2.1. Research Area
2.2. Pilot Program
2.3. Data Sources
2.3.1. Soil Data
2.3.2. Channel Data
2.4. Model Building
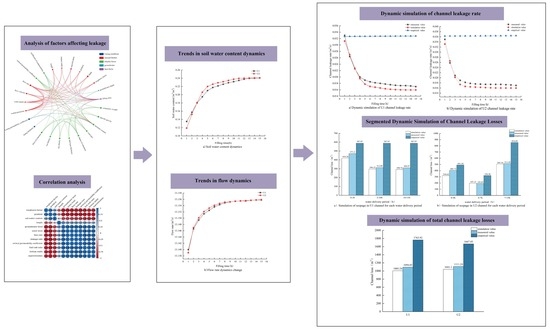
2.4.1. Correlation Analysis of Influencing Factors
2.4.2. Dynamic Simulation Model of Channel Leakage Rate Based on Multiple Regression
3. Results
3.1. Parametric Simulation Results
3.2. Experimental Validation
3.2.1. Dynamic Simulation of Channel Leakage Rate
3.2.2. Leakage Loss Simulation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mao, X.; Yao, L.-Q.; Feng, S.-Y.; Wang, Y.-Y. Numerical simulation on canal seepage and soil water distribution for concrete lining canal with layered soil structure. J. Hydraul. Eng. 2011, 42, 949–955. [Google Scholar]
- National Development and Reform Commission, Ministry of Water Resources. Implementation Plan for Supporting Water Saving Renovation of Large and Medium Sized Irrigation Districts in China (2016–2020) [EB/OL] 2017-05-10. Available online: http://www.jsgg.com.cn/Index/Display.asp?NewsID=21849 (accessed on 1 June 2021).
- Luo, Y.F.; Cui, Y.L.; Zheng, Z.J. Research progress on methods of quantifying seepage from rivers and canals. Adv. Water Sci. 2005, 16, 444–449. [Google Scholar]
- Ye, L.; Ting, Y.; Rong, H.Z.; Yi, B.L.; Wen, J.Z.; Xiao, Y.M. Irrigation Canal System Delivery Scheduling Based on a Particle Swarm Optimization Algorithm. Water 2018, 10, 1281. [Google Scholar]
- Dilini, D.; Hector, M.; Syed, K.S.; Halgamuge, M.N. A novel generic optimization method for irrigation scheduling under multiple objectives and multiple hierarchical layers in a canal network. Adv. Water Resour. 2017, 105, 188–204. [Google Scholar]
- Santhi, C.; Pundarikanthan, N.V. A new planning model for canal scheduling of rotational irrigation. Agric. Water Manag. 2000, 43, 327–343. [Google Scholar] [CrossRef]
- Mishra, A.; Verma, H.C.; Singh, R. Alternative rotational delivery scheduling for better water regime in canal command. J. Irrig. Drain. Eng. 2008, 134, 175–184. [Google Scholar] [CrossRef]
- Li, M.; Fu, Q.; Singh, V.P.; Liu, D.; Li, T.; Zhou, Y. Managing agricultural water and land resources with tradeoff between conomic, environmental, and social considerations: A multi-objective non-linear optimization model under uncertainty. Agric. Syst. 2020, 178, 102685. [Google Scholar] [CrossRef]
- Shah, Z.; Gabriel, H.; Haider, S.; Jafri, T. Analysis of seepage loss from concrete lined irrigation canals in Pun-jab, Pakistan. Irrig. Drain. 2020, 69, 668–681. [Google Scholar] [CrossRef]
- Zhang, Q.; Chai, J.; Xu, Z.; Qin, Y. Investigation of irrigation canal seepage losses through use of four different methods in Hetao Irrigation District, China. J. Hydrol. Eng. 2017, 3, 05016035. [Google Scholar] [CrossRef]
- Akkuzu, E. Usefulness of empirical equations in assessing canal losses through seepage in concrete-lined canal. J. Irrig. Drain. Eng. 2012, 138, 455–460. [Google Scholar] [CrossRef]
- Men, B.H. Discussion on the formula for channel flow loss and water utilization coefficient. China Rural Water Resour. Hydropower 2000, 2, 33–34. [Google Scholar]
- Xie, C.B.; Lance, J.M.; Cui, Y.L.; Bai, M.J.; Huang, B.; Cai, L.G. Exploring the empirical formula for water leakage loss in large and medium-sized irrigation areas’ main channels. China Rural Water Resour. Hydropower 2003, 2, 20–22. [Google Scholar]
- Wang, B.C. Improved formula for calculating channel leakage loss and water utilization coefficient. Agric. Water Conserv. Small Hydropower 1986, 08, 20–21. [Google Scholar]
- Zhang, F.; Cai, Y.P.; Guo, P.; Qian, T.; Wang, X. Estimation method of leakage in trunk and branch canals of irrigation areas and its application in optimal allocation of water resources. J. Agric. Eng. 2021, 37, 140–147. [Google Scholar]
- Liao, X.C.; Hu, T.S. Research on the Optimal Water Distribution Model of Canal System Based on the Dynamic Change Characteristics of Water Transmission Loss. J. Water Resour. 2021, 52, 850–861. [Google Scholar]
- Aller, L.; Lehr, J.H.; Petty, R.; Bennett, T. DRASTIC: A Standardized System to Evaluate Ground Water Pollution Potential Using Hydrogeologic Settings. In Petroleum Hydrocarbons and Organic Chemicals in Ground Water: Prevention, Detection and Restoration; National Water Well Association: Worthington, OH, USA, 1987; pp. 38–57. [Google Scholar]
- Li, H.X.; Fan, G.S. Experimental study on the dominant factors affecting the infiltration capacity of unsaturated soil bed. J. Water Resour. 2009, 40, 630–634. [Google Scholar]
- Hou, H.M.; Dai, X.L.; Wang, Z.J. Study on the effect of different soil structures on water loss in channels. Gansu Sci. Technol. 2009, 25, 44–47. [Google Scholar]
- Fan, Y.; Ma, L.; Wei, H.; Zhu, P. Numerical investigation of wetting front migration and soil water distribution under vertical line source irrigation with different influencing factors. Water Supply 2021, 21, 2233–2248. [Google Scholar] [CrossRef]
- Wang, X.L.; Qu, Z.G.; Lai, T.; Ren, G.F.; Wang, W.K. Enhancing water transport performance of gas diffusion layers through coupling manipulation of pore structure and hydrophobicity. J. Power Sources 2022, 525, 231121. [Google Scholar] [CrossRef]
- Wang, X.L.; Qu, Z.G.; Ren, G.F. Collective enhancement in hydrophobicity and electrical conductivity of gas diffusion layer and the electrochemical performance of PEMFCs. J. Power Sources 2023, 575, 233077. [Google Scholar] [CrossRef]
- Xiao, X.; Wang, X.G.; Tan, D. Comparison of several empirical formulas for calculating channel leakage loss. J. Wuhan Univ. (Eng. Ed.) 2016, 49, 365–371. [Google Scholar] [CrossRef]
- Li, R.X. Comparison of leakage process method and fixed water level method in hydrostatic seepage measurement of channels. J. Water Resour. Archit. Eng. 1991, 2, 50–53. [Google Scholar]
- Li, M.; Liu, T.; Lu, Y.; Duan, L.; Zhang, J.; Zhou, Y. Research on soil infiltration process and conversion function in a semi-arid grassland-type watershed. J. Water Resour. 2019, 50, 936–946. [Google Scholar] [CrossRef]
- Kratz, D.B. Lining of Irrigation Canals; He, P., Translator; Water Resources Press: Beijing, China, 1980. [Google Scholar]







| Channel Number | Length (m) | Bottom Width (m) | Superelevation (m) | Flow Velocity (m3/s) | Designed Discharge (m3/s) | Soil Texture | Water Permeability | Roughness Factor | Gradient | Cross-Section Form |
|---|---|---|---|---|---|---|---|---|---|---|
| U1 | 1000 | 6 | 0.5 | 0.852 | 14.7 | medium frequency transformer loam | general | 0.02 | 1/5000 | trapezium |
| U2 | 1000 | 6 | 0.5 | 0.827 | 13.9 | light flux loam | strong | 0.02 | 1/5000 | trapezium |
| Name of Branch Canal | Length (m) | Cross-Section Form | Bottom Width (m) | Depth (m) |
|---|---|---|---|---|
| No.1 branch canal | 7320 | trapezium | 6 | 0.5 |
| No.2 branch canal | 3270 | trapezium | 6 | 0.5 |
| No.3 branch canal | 2250 | trapezium | 6 | 0.5 |
| No.4 branch canal | 1100 | trapezium | 6 | 0.5 |
| No.5 branch canal | 60 | trapezium | 6 | 0.5 |
| No.6 branch canal | 4550 | trapezium | 6 | 0.5 |
| No.7 branch canal | 3930 | trapezium | 6 | 0.5 |
| No.8 branch canal | 1250 | trapezium | 6 | 0.5 |
| No.9 branch canal | 100 | trapezium | 6 | 0.5 |
| No.10 branch canal | 2640 | trapezium | 5 | 0.5 |
| No.11 branch canal | 10 | trapezium | 5 | 0.5 |
| No.12 branch canal | 470 | trapezium | 5 | 0.5 |
| Model | Non-Standardized Coefficient | Standardized Coefficient | t | Significance | ||
|---|---|---|---|---|---|---|
| B | STDERR | Beat | ||||
| 1 | (constant) | 0.011 | 0.368 | - | 28.682 | 0.689 |
| length | 3.14 × 10−5 | 0.598 | 0.037 | 0.366 | 0.723 | |
| flow rate | 0 | 0.211 | 0.944 | 9.25 | 0.587 | |
| soil water content | 0.219 | 0.109 | 0.293 | 2.017 | 0.083 | |
| water level | 0.015 | 0.852 | 0.188 | 0.124 | 0.006 | |
| 2 | (constant) | 0.009 | 0.027 | - | 0.343 | 0.764 |
| length | 5.02 × 10−4 | 0.397 | −0.06 | −0.399 | 0.728 | |
| superelevation | −0.034 | 0.029 | −0.808 | −1.188 | 0.357 | |
| roughness factor | 0.47 | 0.259 | 0.627 | 1.816 | 0.211 | |
| drawdown | −0.023 | 0.246 | −0.032 | −0.095 | 0.933 | |
| flow rate | 0.001 | 0.514 | 1.603 | 2.027 | 0.18 | |
| 3 | (constant) | −0.004 | 0.01 | - | −0.355 | 0.029 |
| length | 2.54 × 10−4 | 0.652 | −0.03 | −0.273 | 0.83 | |
| gradient | 46.103 | 22.298 | 1.081 | 2.068 | 0.047 | |
| roughness factor | 0.747 | 0.252 | 0.997 | 2.963 | 0.039 | |
| water level | 0.007 | 0.004 | 1.138 | 1.66 | 0.031 | |
| flow rate | 0.0004 | 0.323 | 0.847 | 1.152 | 0.014 | |
| groundwater level | −0.001 | 0.981 | −0.178 | −1.027 | 0.048 | |
| soil void ratio | −0.037 | 0.028 | −0.557 | −1.303 | 0.028 | |
| vertical permeability coefficient | 89.54 | 41.917 | 1.218 | 2.136 | 0.020 | |
| soil water content | −0.032 | 0.019 | −0.292 | −1.652 | 0.033 | |
| Model Summary | |||||
|---|---|---|---|---|---|
| Model | R | R2 | Adjusted R2 | Errors in Standard Estimates | Debin-Watson Coefficient |
| 1 | 0.999 | 0.998 | 0.982 | 0.000262 | 2.732 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Yang, J.; Hao, X.; Cui, B.; Yang, S. Dynamic Simulation Model of Channel Leakage Based on Multiple Regression. Sustainability 2023, 15, 14904. https://doi.org/10.3390/su152014904
Ma J, Yang J, Hao X, Cui B, Yang S. Dynamic Simulation Model of Channel Leakage Based on Multiple Regression. Sustainability. 2023; 15(20):14904. https://doi.org/10.3390/su152014904
Chicago/Turabian StyleMa, Jianqin, Jiangshan Yang, Xiuping Hao, Bifeng Cui, and Shuoguo Yang. 2023. "Dynamic Simulation Model of Channel Leakage Based on Multiple Regression" Sustainability 15, no. 20: 14904. https://doi.org/10.3390/su152014904