Scaled Model for Studying the Propagation of Radio Waves Diffracted from Tunnels
Abstract
:1. Introduction
2. The Indoor–Outdoor Model
2.1. Indoor Multi-Ray Propagation Model
2.2. Outdoor Diffraction from Tunnels
2.3. Numerical Procedure
2.4. Uniform Illumination: Test Case
3. Experimental Setup
4. Results
4.1. Modeling Results: Full-Scale Model
4.2. Experimental and Modeling Results: Scaled Model—Tunnel Exit
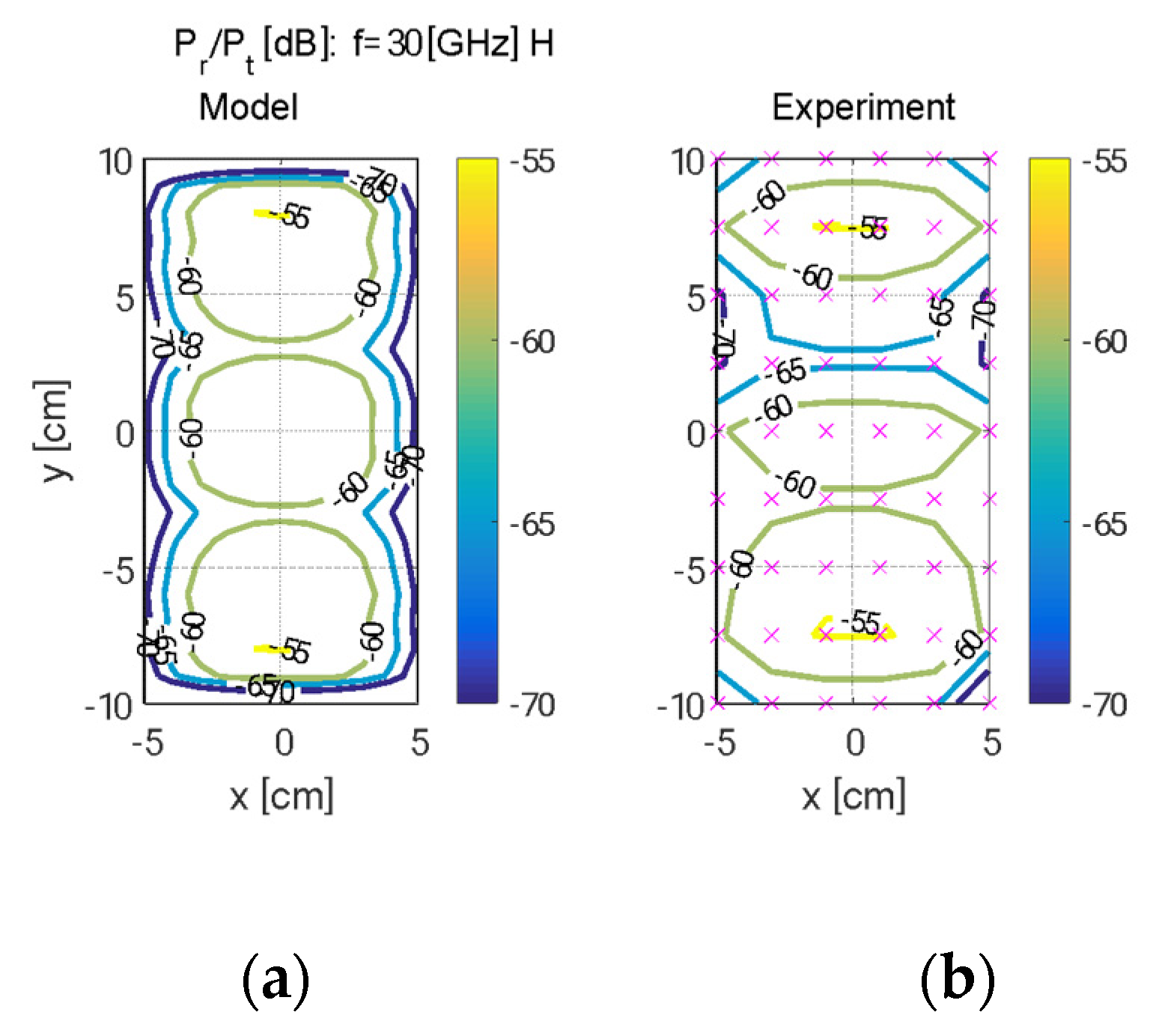
4.3. Experimental and Modeling Results: Scaled Model—Diffraction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rappaport, T.S. Wireless Communications Principles and Practice, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Molisch, A.F. Wireless Communications, 2nd ed.; Wiley Publishing: Hoboken, NJ, USA, 2011. [Google Scholar]
- Hrovat, A.; Kandus, G.; Javornik, T. A Survey of radio propagation modeling for tunnels. IEEE Commun. Surv. Tutor. 2014, 16, 658–669. [Google Scholar] [CrossRef]
- Zhang, Y.; Sood, N.; Sarris, C.D. Propagation modeling in complex tunnel environments: A comparison of vector parabolic equation and ray-tracing solutions. In Proceedings of the 2017 International Conference on Electromagnetics in Advanced Applications (ICEAA), Verona, Italy, 11–15 September 2017; pp. 1676–1679. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; Sun, J.; Wang, C.X.; Ge, X. Impact of different parameters on channel characteristics in a high-speed train ray tracing tunnel channel model. In Proceedings of the 2017 IEEE 85th Vehicular Technology Conference (VTC Spring), Sydney, Australia, 4–7 June 2017; pp. 1–5. [Google Scholar]
- Forooshani, A.E.; Bashir, S.; Michelson, D.G.; Noghanian, S. A survey of wireless communications and propagation modeling in underground mines. IEEE Commun. Surv. Tutor. 2013, 15, 1524–1545. [Google Scholar] [CrossRef]
- Samad, M.A.; Choi, S.W.; Kim, C.S.; Choi, K. Wave propagation modeling techniques in tunnel environments: A Survey. IEEE Access 2023, 11, 2199–2225. [Google Scholar] [CrossRef]
- Zhou, C.; Plass, T.; Jacksha, R.; Waynert, J.A. RF Propagation in mines and tunnels: Extensive measurements for vertically, horizontally, and cross-polarized signals in mines and tunnels. IEEE Antennas Propag. Mag. 2015, 57, 88–102. [Google Scholar] [CrossRef]
- Zhou, C. Ray tracing and modal methods for modeling radio propagation in tunnels with rough walls. IEEE Trans. Antennas Propag. 2017, 65, 2624–2634. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.; Jacksha, R. Modeling and measurement of radio propagation in tunnel environments. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 1431–1434. [Google Scholar] [CrossRef] [PubMed]
- Hossain, F.; Geok, T.K.; Rahman, T.A.; Hindia, M.N.; Dimyati, K.; Ahmed, S.; Tso, C.P.; Rahman, A.; Ziela, N. An efficient 3-D ray tracing method: Prediction of indoor radio propagation at 28 GHz in 5G network. Electronics 2019, 8, 286. [Google Scholar] [CrossRef]
- Zhao, C.; Hou, W.; Wang, J. Effect of antenna Location and polarization on radio wave propagation in tunnel. In Proceedings of the 2019 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Guangzhou, China, 19–22 May 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, J.; Hou, W.; Li, Y.; Al, B. Optimized scheme of antenna diversity for radio wave coverage in tunnel environment. IEEE Access 2020, 8, 127226–127233. [Google Scholar] [CrossRef]
- Oladimeji, T.T.; Kumar, P.; Oyie, N.O. Propagation path loss prediction modelling in enclosed environments for 5G networks: A review. Heliyon 2022, 8, e11581. [Google Scholar] [CrossRef] [PubMed]
- Chatzinotas, S.; Hu, Y. Refracting RIS aided hybrid satellite-terrestrial relay networks: Joint beamforming design and optimization. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3717–3724. [Google Scholar]
- Lin, Z.; Lin, M.; Champagne, B.; Zhu, W.P.; Al-Dhahir, N. Secrecy-energy efficient hybrid beamforming for satellite-terrestrial integrated networks. IEEE Trans. Commun. 2021, 69, 6345–6360. [Google Scholar] [CrossRef]
- Lin, Z.; An, K.; Niu, H.; Hu, Y.; Chatzinotas, S.; Zheng, G.; Wang, J. SLNR-based secure energy efficient beamforming in multibeam satellite systems. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 2085–2088. [Google Scholar] [CrossRef]
- Sani, U.S.; Malik, O.A.; Ching Lai, D.T. Improving path loss prediction using environmental feature extraction from satellite images: Hand-crafted vs. Convolutional neural network. Appl. Sci. 2022, 12, 7685. [Google Scholar] [CrossRef]
- Ma, R.; Yang, W.; Guan, X.; Lu, X.; Song, Y.; Chen, D. Covert mmWave communications with finite blocklength against spatially random wardens. IEEE Internet Things J. 2024, 11, 3402–3416. [Google Scholar] [CrossRef]
- Rapaport, L.; Pinhasi, G.A.; Pinhasi, Y. Millimeter wave propagation in long corridors and tunnels—Theoretical model and experimental verification. Electronics 2020, 9, 707. [Google Scholar] [CrossRef]
- Gerasimov, J.; Balal, N.; Liokumovitch, E.; Richter, Y.; Gerasimov, M.; Bamani, E.; Pinhasi, G.A.; Pinhasi, Y. Scaled modeling and measurement for studying radio wave propagation in tunnels. Electronics 2021, 10, 53. [Google Scholar] [CrossRef]
- Taragin, Y.; Rapaport, L.; Elkayamn, N.; Pinhasi, G.A.; Pinhasi, Y. High-resolution delay spread of wide-band wireless link in long tunnels- Theory and experimental verification. Electronics 2022, 11, 2140. [Google Scholar] [CrossRef]
- Glikstein, O.; Hanina, S.; Balal, N.; Pinhasi, G.A.; Pinhasi, Y. Indoor-outdoor of wireless link propagation from tunnels and long corridors. In Proceedings of the 2022 IEEE International Conference on Computer, Information, and Telecommunication Systems, CITS 2022, Piraeus, Greece, 13–15 July 2022; pp. 112–115. [Google Scholar]
- Galyamin, S.N.; Vorobev, V.V. Diffraction at the open end of dielectric-lined circular waveguide. IEEE Trans. Microw. Theory Tech. 2021, 70, 3087–3795. [Google Scholar] [CrossRef]
- Galyamin, S.N.; Vorobev, V.V.; Tyukhtin, A.V. Diffraction at the open-ended dielectric-loaded circular waveguide: Rigorous approach. IEEE Trans. Microw. Theory Tech. 2021, 69, 2429–2438. [Google Scholar] [CrossRef]
- Goodmanm, J.W. Introduction to Fourier Optics; Roberts and Company Publishers: Greenwood Village, CO, USA, 2005. [Google Scholar]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes in C, The Art of Scientific Computing, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992; ISBN 0-521-43108-5. [Google Scholar]

















| Wall | Normal Vector | Incidence Angle | Wave Polarity | |
|---|---|---|---|---|
| Vertical, V | Horizontal, H | |||
| Top/bottom: (i = U, D) | θi | TM (||) | TE (⊥) | |
| Side walls: (i = R, L) | θi | TE (⊥) | TM (||) | |
| Parameter | Normal Vector | Units | Full-Scale Model | Scaled Model |
|---|---|---|---|---|
| Tunnel width | 2a | [m] | 1 | 0.10 |
| Tunnel height | 2b | [m] | 2 | 0.20 |
| Tunnel length | L | [m] | 25 | 2.5 |
| Frequency | f | [GHz] | 1 and 3 | 10 and 30 |
| Distance from tunnel exit | d | [m] | 40 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Glikstein, O.; Pinhasi, G.A.; Pinhasi, Y. Scaled Model for Studying the Propagation of Radio Waves Diffracted from Tunnels. Electronics 2024, 13, 1983. https://doi.org/10.3390/electronics13101983
Glikstein O, Pinhasi GA, Pinhasi Y. Scaled Model for Studying the Propagation of Radio Waves Diffracted from Tunnels. Electronics. 2024; 13(10):1983. https://doi.org/10.3390/electronics13101983
Chicago/Turabian StyleGlikstein, Ori, Gad A. Pinhasi, and Yosef Pinhasi. 2024. "Scaled Model for Studying the Propagation of Radio Waves Diffracted from Tunnels" Electronics 13, no. 10: 1983. https://doi.org/10.3390/electronics13101983






