Optimizing Microwave-Assisted Extraction from Levisticum officinale WDJ Koch Roots Using Pareto Optimal Solutions

Abstract

The current research trend is not only focused on advanced techniques to intensify the extraction of bioactive compounds from plants, but also on the optimization process. The objective of this work was the implementation of the multiple criteria analysis using navigation on Pareto sets to determine the optimal parameters for the microwave-assisted extraction of Levisticum officinale WDJ Koch roots in order to obtain the maximum efficiency of the antioxidant potential of the extracts. The optimized parameters were extraction time, microwave power, and plant biomass/solvent ratio, while the evaluation criteria were based on the total phenols, flavonoids, reducing sugars, and antioxidant capacity. It was shown that the process parameters analyzed, i.e., biomass/solvent ratio, process time, and microwave power, determined the extraction efficiency of total phenolic content (TPC). A different observation was made for the analysis of total flavonoid content (TFC) and total antioxidant potential (TAA). Compared to the assessment of TFC and TAA, a completely different trend was observed for the analysis of total reducing sugars (RSC). Sets of Pareto optimal, compromise, and preferred solutions were identified that will maximize the efficiency of the extraction of bioactive compounds from biomass. Due to the determined number of Pareto optimal solutions, an approach related to the introduction of preferences in the optimization procedure was applied. It was shown that for a satisfactory level of bioactive compounds, extraction should be carried out at a maximum microwave power of 750 W. Preferred solutions were obtained for root biomass to water ratios ranging from 0.0536 g/mL to 0.0679 g/mL. The preferred optimal time for microwave-assisted water extraction ranged from 64.2857 to 85.7143 s.

1. Introduction

The plant Levisticum officinale WDJ Koch, or lovage, is a member of the Apiaceae family. It is a rich source of many classes of secondary metabolites, with a broad spectrum of pharmacological and therapeutic activities [1,2,3,4,5]. Many active compounds, such as phenolic compounds or flavonoids from plants, have a range of beneficial health properties. However, its potential is not only limited to pharmacological applications [6,7,8]. Indeed, studies show that the active compounds contained in plant extracts may also have the potential to biostimulate crop plants [8,9]. The extraction of phytochemicals from lovage roots has been studied, but research in this area has mainly focused on conventional solvent extraction and oil extraction efficiency. Currently, advanced extraction techniques for enhancing the extraction of phenolic compounds from herbal materials are being researched, which include pressurized extraction (PLE) [10], microwave-assisted extraction (MAE) [11] and ultrasound [12], or supercritical fluid extraction [13]. However, it is important to underline the fact that an extraction technique can be described as “green” and environmentally friendly, as well as cheap, when the used solvent is water. Currently, among extraction technologies, microwave-assisted extraction (MAE) deserves special attention [14,15]. Its main advantages over conventional methods, include, in particular, the increased speed of the process, as well as the improved efficiency of the extraction of bioactive compounds at a reduced cost [16,17]. A study by Vinatoru et al. [18] indicates that microwave-assisted extraction of the plant matrix is a beneficial technique because it is associated with the homogeneous internal heating of the entire volume of the material, resulting in increased pressure inside the plant cells, causing them to burst and efficiently release the desired bioactive compounds. However, for the extraction efficiency and stability of the extracted compounds, the process parameters should be selected individually for each plant matrix. It should also be emphasized that, despite the fact that each extraction technique is distinguished by certain advantages and limitations, each should be optimized individually with respect to the plant material and phytochemicals of interest (maximization of extraction) [19].

As mentioned earlier, the beneficial pharmacological properties of aromatic or herbal plants are generally related to the presence of a variety of plant secondary metabolites with different structures. From the point of view of crop physiology, polyphenolic compounds with strong antioxidant capacity can be used in crop biostimulation [20]. Indeed, phenolic compounds influence plant growth and development by stimulating seed germination, increased biomass accumulation, and improving plant metabolism [21,22,23]. Extracts with high polyphenol content have different compositions, depending on the source of extraction, extraction conditions and techniques, and extraction solvent. Consequently, these aspects need to be investigated for future agronomic applications [23]. The benefits of phytochemicals, as indicated in the subject literature, and the drive to replace synthetic fertilizers and crop protection products with natural substances have led to increased research efforts to discover and use bioactive compounds from natural sources such as aromatic plants for crop biostimulation [23,24,25]. Due to the fact that there is a growing awareness of the negative impact of agrochemicals and the ongoing transformation towards “green agriculture”, the use of natural biostimulants is becoming increasingly popular globally [26]. Research indicates that natural biostimulants have a positive effect on overall plant productivity and yield quality, as well as on reducing the impact of biotic and abiotic stress-inducing factors on plants [26,27].

The objective of this research was the implementation of the multiple criteria analysis using navigation on Pareto sets to determine the optimal parameters for the microwave-assisted extraction of Levisticum officinale roots in order to maximize the antioxidant potential of the extracts. The parameters for optimization were extraction time, microwave power, and plant biomass/solvent ratio, while the evaluation criteria were based on the total phenolic content, flavonoids, reducing sugars, and antioxidant capacity (as determined by DPPH) of the extracts. It is hoped that such systematic studies will greatly expand the knowledge regarding the application of microwave-assisted extraction for the advanced processing of lovage into high-value natural components for agronomic applications.

2. Materials and Methods

2.1. Plant Material

The dried roots of an organically grown Levisticum officinale L. (sourced from Runo Polska, PL-EKO 07 EU Organic Farming, Poland) were ground into powder (fraction size of 500 μm). The ground powder was stored at 4 °C in airtight bags until further use.

2.2. Microwave-Assisted Extraction (MAE)

The extraction of lovage root biomass was carried out using 100 mL of water (at pH 7.0) as the extraction solvent in a laboratory microwave oven (JT358, Whirlpool, Benton Harbor, MI, USA). The device is equipped with a digital control system for regulating irradiation time and microwave power. For MAE, the independent variables were: extraction time (30, 60, and 90 s); microwave power (550, 650, and 750 W), and the ratio of plant biomass/water (w/v) (2.5 g/100 mL (0.025 g/mL), 5 g/100 mL (0.050 g/mL), and 7.5 g/100 mL (0.075 g/mL)). Each process was carried out in triplicate. After MAE treatment, the extract was centrifuged (9500 rpm, 20 min) and filtered through a Büchner funnel lined with Whatman No. 1 filter paper, and the supernatant was collected in dark glass bottles and stored at 4 °C, pending further use and analysis.

2.3. Bioactive Characterization of Obtained Extracts

The total content of phenolic compounds (TPC) was determined in the obtained extracts from Levisticum officinale based on the Ribeiro method [28], using Folin–Ciocalteu reagent. The quantitative assessment of TPC levels in the extracts was expressed as mg gallic acid equivalent/g extract. The extracts were also assessed for total flavonoid content (TFC), according to the method of Iqbal et al. [29]. TFC levels were expressed as the catechin equivalent (μmol/L). The total antioxidant activity (TAA) was also determined using the DPPH (2,2-diphenyl-1-picrylhydrazyl) test, employing the method of Lee et al. [30]. The scavenging activity (inhibition of the DPPH radical by the sample) was expressed as the percentage of DPPH decrease. The reducing sugars content (RSC) was analyzed, based on the method using DNSA (3,5-dinitrosalicylic acid) proposed by Krivorotova and Sereikaite [31]. The total concentration of reducing sugars in the samples was expressed as g of D-glucose equivalent (GE) per L of extract.

2.4. Mathematical Model

The analysis of the possibility of increasing the efficiency of the microwave-assisted water extraction of bioactive compounds from the roots of Levisticum officinale was based on the created mathematical models and optimization tools based on computer computation and simulation packages (Matlab R2021a). The optimization procedure began with the creation of multivariate regression models (experimental data). The decision variables were sample/solvent ratio (g/mL) (x₁), microwave power (W) (x₂), and time of microwave assisted extraction (s) (x₃). Multivariate polynomials were used to define the relationship between the criteria and decision variables:

$$\begin{gathered} y_{reg}\left(x_1,x_2,x_3\right)=a_0+a_1\ast x_1+a_2\ast x_2+a_3\ast x_3+a_4\ast x_1\ast x_2+a_5\ast x_1\ast x_3+a_6\ast x_2\ast x_3+a_7\ast x_1^2+a_8 \\ \ast x_2^2+a_9\ast x_3^2 \end{gathered}$$

(1)

The predictive accuracy of the models was analyzed based on the values of the R² coefficient, adjusted R², and MSE (mean squared prediction error). R² is defined as the ratio of the sum of squares of regression (SSR) and the total sum of squares (SST). SSR is defined as [32]:

$$R^2=\frac{SSR}{SST}=1-\frac{SSE}{SST}$$

(2)

The adjusted R² was also determined:

$$Adj R^2=1-\frac{SSE(n-1)}{SST\left(v\right)}$$

(3)

• $v$—degrees of freedom
• $SSE$—sum of squares due to error
• $SST$—the sum of squares about the mean

The mean squared prediction error (MSE) was determined as the mean square deviation between the experimental data and the values resulting from the adopted model:

$$MSE=\frac{SSE}{v}$$

(4)

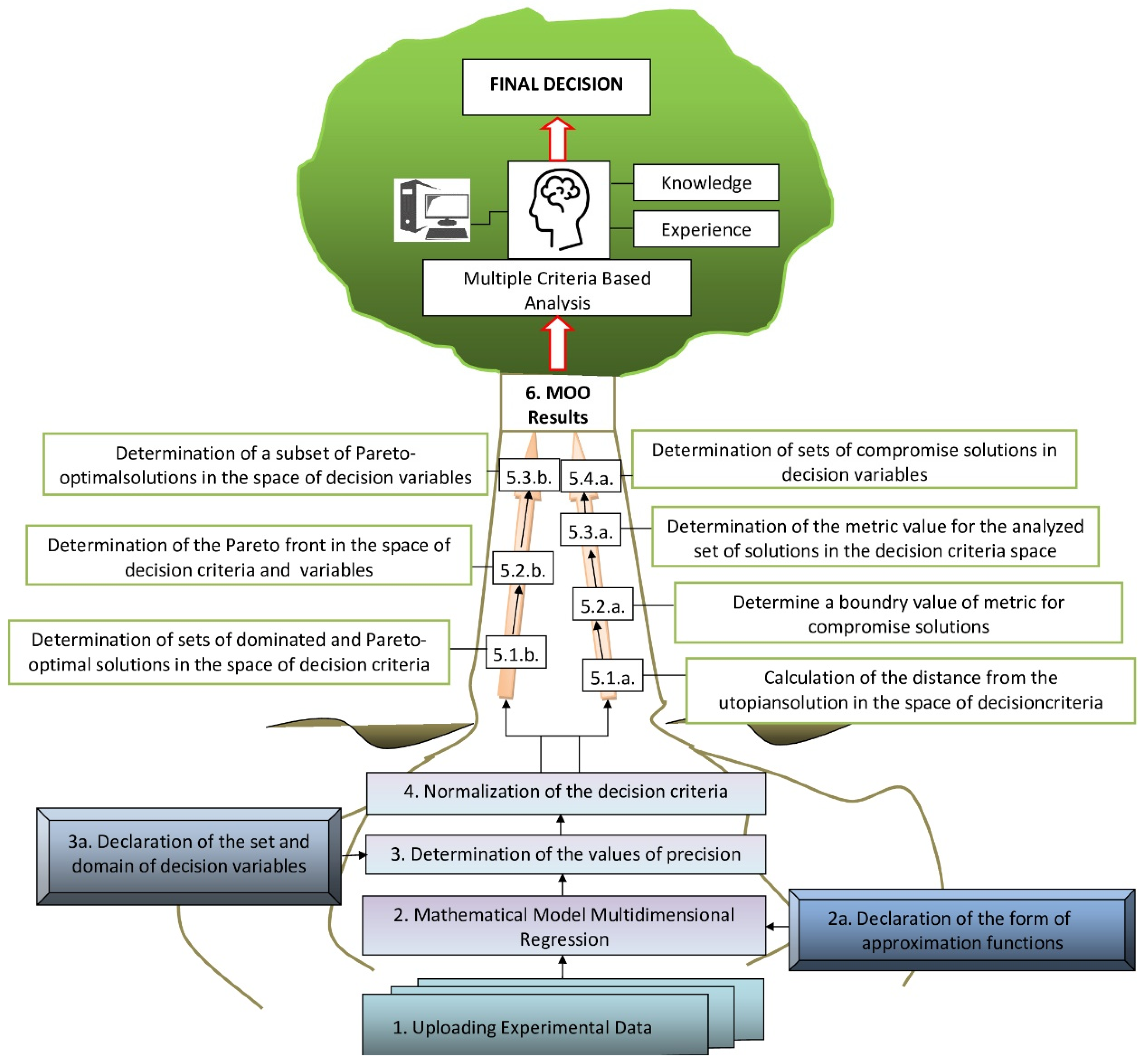
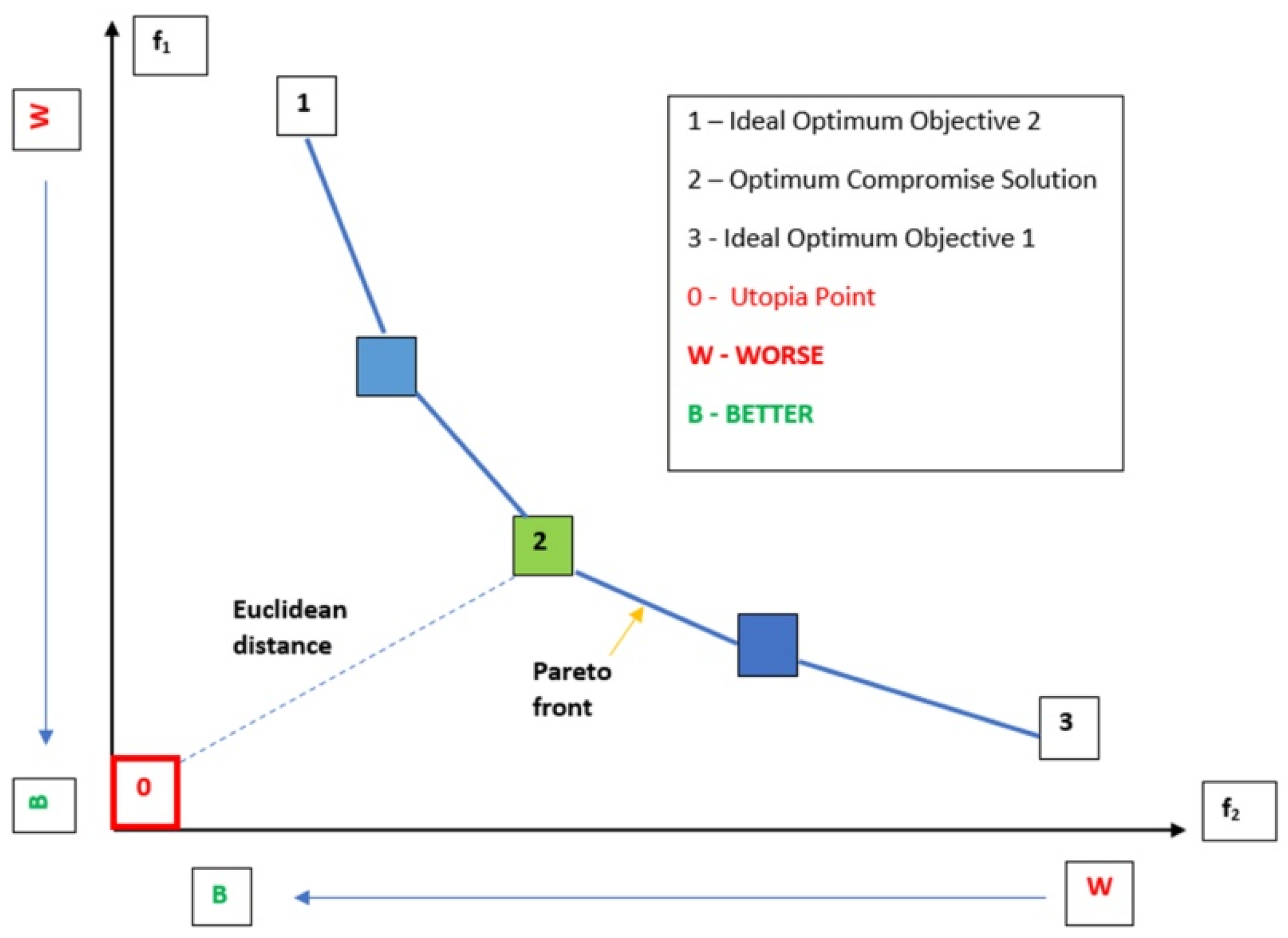
2.5. Multi-Objective Optimization

In the presented optimization task, a four-dimensional space of decision criteria was adopted: K = [K₁, K₂, K₃, K₄] ∈ R⁴. The objective of the multi-criteria optimization task was to produce an extract from the roots of Levisticum officinale, characterized by the maximum value of all the decision criteria:

$$K_1\to max,K_2\to max,K_3\to max,K_4\to max$$

(5)

The optimization procedure is shown in Figure 1.

The decision criteria corresponded to the individual quality characteristics of extracts from Levisticum officinale: K₁—TPC (total phenolic content) (mg GAE/g); K₂—TFC (total flavonoids content) (μmol CAT/L); K₃—TAA (total antioxidant activity) (DPPH-% inh); K₄—RSC (reducing sugar content) (g GE/L). These criteria were calculated for a specific set of decision variables for the microwave-assisted extraction process. The following parameters of the extraction process were adopted as decision variables: x₁—sample/solvent ratio (g/mL), x₂—microwave power (W), and x₃—time (s).

The domain of decision variables was defined by the following formula:

$$D=x_1\times x_2\times x_3$$

(6)

Constraints imposed on decision variables x₁–x₃ were assumed as follows:

$$x_1\in 〈0.025;0.075〉[\mathrm{g}/\mathrm{m}\mathrm{L}]$$

(7)

$$x_2\in 〈550;750〉\left[\mathrm{W}\right]$$

(8)

$$x_3\in 〈30;90〉\left[\mathrm{s}\right]$$

(9)

The values of the four individual criteria for a fixed domain of the set of variables D were determined based on a multivariate approximation of the experimental results.

The multi-objective optimization task consisted of determining a set of solutions in set D for decision criteria that meet the conditions for achieving the maximum values.

The decision criteria were scaled to dimensionless values and normalized as follows:

$$K_i^{\left(n\right)}=\frac{K_i^{max}-K_i}{K_i^{max}-K_i^{min}} i=\mathrm{1,2},\mathrm{3,4} k_i^{\left(n\right)}\in 〈0;1〉$$

(10)

where K_i^min and K_i^max are the smallest and largest values of the criteria for the analyzed domain of the decision variables, respectively. The standardization procedure used allows for comparison of the values of the criteria describing different quantities and expressed in different units. The maximum value of the actual criterion corresponds to the value 0 in the space of standardized criteria.

The set of all possible Pareto optimal solutions was determined, and then the explicit form of the set of dominated and non-dominated solutions for extracts from Levisticum officianle in the criteria space was determined (set in a four-dimensional criteria space). In order to analyze and visualize these sets, subsets of the four-dimensional space (K₁, K₂, K₃, K₄) in three-dimensional and two-dimensional criterion spaces were considered [33].

2.6. Smart Pareto Filter—Pareto Frontier Exploration Using Weighting of Decision Criteria

The method for obtaining a smart representation was used. In the proposed method, the multi-objective optimization of the Pareto front topology is based on the weighted sum method. The weighted sum method is a useful approach for many practical multi-subject optimization problems [34,35]. The procedure diagram is shown in Figure 2. The following were adopted for the decision criteria:

$$K=\sqrt{K_1^2+K_2^2+K_3^2+K_4^2}$$

(11)

After entering the importance of individual criteria, the following form was obtained:

$$K=\sqrt{w_1{K}_1^2+w_2{K}_2^2+w_3{K}_3^2+w_4{K}_4^2}$$

(12)

The criteria were assigned weights based on the following equation:

$$w_1+w_2+w_3+w_4=1$$

(13)

Figure 2. Methodology of smart Pareto set.

Figure 2. Methodology of smart Pareto set.

For criteria K₁–K₃, the value of w₁, w₂, and w₃ was 0.3. However, for K₄, the value of w₄ was 0.1.

Using this approach, it was possible to determine the so-called “preferred” solutions from the Pareto front.

2.7. Reducing the Set of Pareto Optimal Solutions—The Compromise Solutions

In this optimization procedure, the definition of the Utopia point was adopted, i.e., the ideal point that maximizes the goals simultaneously (the so-called unattainable point) [36]. Therefore, the concept of achievable compromise solutions on the Pareto front, with the minimum distance from the Utopia point (d_U), was introduced. To find this compromise solution on the Pareto front, first, the objective functions were normalized to the range [0, 1]. A graphical representation of the procedure is shown in Figure 3.

In the next step, the Euclidean distance of all solutions on the Pareto front was determined, measured from the ideal point. Therefore, in order to analyze the set of possible solutions, a Euclidean metric of the form was introduced in the space of the standardized decision criteria, as follows:

$$d_U=d(K_{0}K)=\sqrt{\sum _{i=1}^4{K}_i^2}$$

(14)

where K₀ = (0, 0, 0, 0) is the origin of the coordinate system, or the so-called Utopian solution.

Pareto optimal solutions with the minimum distance from the Utopia point were indicated as the best solution from a given set (d_U). The obtained solutions can be treated as the best solutions from the obtained Pareto set in terms of the equal satisfaction of the all criteria.

2.8. Statistical Analysis

An analysis was performed in Matlab 7.0 using the F-statistic to test the statistical significance of the model. The values of the F-statistic (F-statistic for testing the final model vs. no model, mean only) allowed for the assessment of the significance of the elements or components of the model. The SSE—the sum of squared errors (residuals)—was given, defined as a numerical value. The SSR—the sum of squares due to regression—or the explained sum of squares (ESS)—the sum of the differences between the predicted value and the mean of the dependent variable—were also calculated, as well as the pval, a vector of p-values for testing whether elements of b are 0.

3. Results

3.1. The Mathematical Models—Multivariate Regression

The first step for the multi-criteria optimization of microwave-assisted extraction (MAE) was to build adequate response models (criteria) of TPC, TFC, TAA, and RSC for the process input parameters (biomass/solvent ratio, microwave exposure time, and microwave power). The effects of the decision variables (extraction process parameters) on the extraction efficiency of phenolic compounds, flavonoids, carbohydrates, and antioxidant potential are shown in Figure 4, Figure 5, Figure 6 and Figure 7.

The regression model for total phenolic content is presented in Equation (1).

$$\begin{gathered} TPC=1235.24+(-2407.77)\ast x_1+(-2.67)\ast x_2+(-6.71)\ast x_3+5.59\ast x_1\ast x_2+22.32\ast x_1\ast x_3+0.012 \\ \ast x_2\ast x_3+(-2830.27)\ast x_1^2+0.0013\ast x_2^2+(-0.012)\ast x_3^2 \end{gathered}$$

(15)

The R² coefficient of 0.813 in good agreement with the Adj R² coefficient of 0.716 (difference = 0.097), with a mean squared prediction error (MSE) value of 212.794 (

Table 1. Indicators of model fit of the experimental results and F-statistics for the decision criteria.

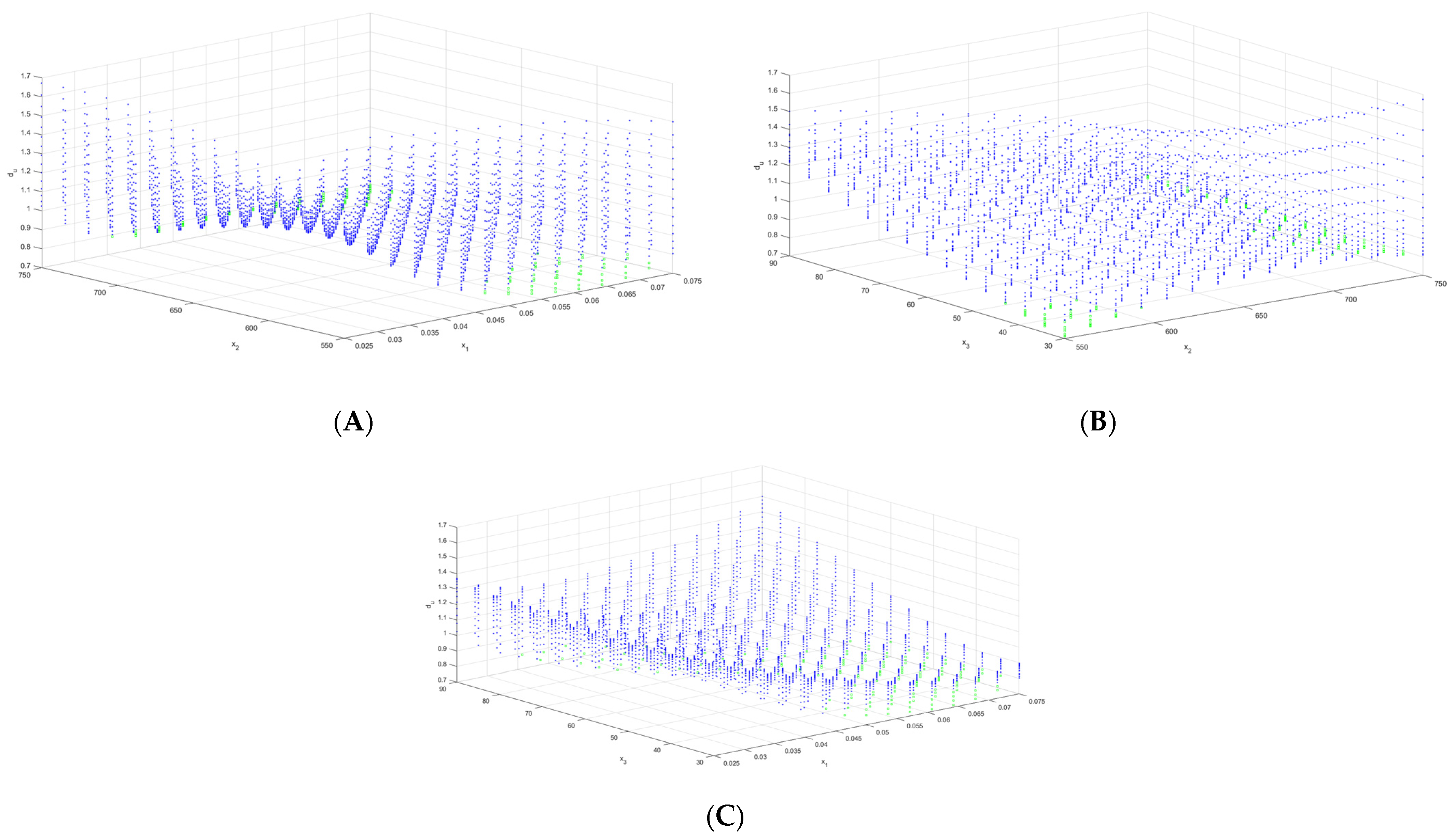
Criteria	MSE	R2	Adj R2	SSE	SSR	F-Value	p-Value
K1	2127.941	0.813	0.716	3.620 × 104	8.970 × 104	4.6842	3.100 × 10−3
K2	1606.676	0.821	0.726	2.730 × 104	1.250 × 105	8.6418	8.510 × 10−5
K3	16.410	0.820	0.723	278.848	1.260 × 103	8.5237	9.290 × 10−5
K4	2.450	0.890	0.830	41.7226	3.180 × 102	14.3846	2.640 × 10−6

Legend: SSE—sum of squared errors (residuals), expressed as a numerical value; SSR—sum of squares due to regression, or explained sum of squares (ESS)—sum of the differences between the predicted value and the mean of the dependent variable; pval—vector of p-values for testing whether elements of b are 0.

), indicating that the model for total polyphenol content (TPC) can be used to navigate the design space.

The regression models for total flavonoid content (criterion K₂) and total antioxidant potential (criterion K₃) reflected the experimental data equally well (Equations (2) and (3)).

$$\begin{gathered} TFC=653.74+1238.19\ast x_1+(-1.16)\ast x_2+(-5.36)\ast x_3+11.97\ast x_1\ast x_2+(-46.98)\ast x_1\ast x_3 \\ +0.0061\ast x_2\ast x_3+(-16119.8)\ast x_1^2+0.0003\ast x_2^2+0.036\ast x_3^2 \end{gathered}$$

(16)

$$\begin{gathered} TAA=201.53+1578.34\ast x_1+(-0.59)\ast x_2+0.558\ast x_3+0.257\ast x_1\ast x_2+(-3.42)\ast x_1\ast x_3+0.0006 \\ \ast x_2\ast x_3+(-13650.1)\ast x_1^2+0.00042\ast x_2^2+(-0.0067)\ast x_3^2 \end{gathered}$$

(17)

The determined values of the R² coefficients were 0.821 and 0.820, respectively, while the adjusted R² values (Adj R²) reached 0.7260 and 0.7225. It was therefore concluded that the generated polynomial equations could be applied to the optimization procedure for the MAE extraction parameters for maximizing the K₂ and K₃ criteria.

The regression equation for RSC is presented in Equation (4).

$$\begin{gathered} RSC=2.95+(-235.05)\ast x_1+0.051\ast x_2+(-0.07)\ast x_3+(-0.29)\ast x_1\ast x_2+(-1.73)\ast x_1\ast x_3+0.00021 \\ \ast x_2\ast x_3+4189.67\ast x_1^2+(-3.43)\ast x_2^2+(-0.00046)\ast x_3^2 \end{gathered}$$

(18)

The best fit of the models to the experimental results was obtained for RSC (reducing sugar content). For this criterion, the R² was 0.8900, with a corrected value for this indicator of 0.8300 (difference of 0.0600). This indicates the predictive ability of the model for RSC.

It was shown that the process parameters analyzed, i.e., biomass/solvent ratio, process time, and microwave power, determined the extraction efficiency of the total phenolic content (TPC). Increased microwave power, to 650 and 750 W, led to increased levels of TPC in aqueous extracts. Similar effects were observed when the microwave exposure time was increased on the plant biomass in the solvent. The high total levels of phenolic compounds in the extracts resulted from the extraction procedure in which the ratio of the Levisticum officinale root biomass to water was the highest. The extracts, obtained with a plant sample to water ratio of 0.075, expressed a higher concentration of the total phenolic compound pool.

A different observation was made for the analysis of total flavonoid content (TFC). Admittedly, all process parameters shaped the value of this criterion, but to a completely different degree than for TPC. It was shown that exceeding the limit of the extraction process parameters led to a decrease in the level of flavonoids in the extracts (Figure 5). In general, prolonging the extraction procedure resulted in an increased TFC content in the samples analyzed. However, when the effect of the ratio of Levisticum officinale root biomass to solvent volume was assessed, it was found that flavonoid extraction reached increased levels for the average indicator analyzed (0.050 g/mL). In addition, it was found that at increased microwave power, of the order of 650 and 750 W, similar amounts of flavonoids were already observed in the extracts.

Similar relationships with the analysis of total flavonoid content were observed when assessing total antioxidant potential (TAA). An occurrence of a certain TAA extreme was noted, and after certain process parameter limits were exceeded, the analyzed quality characteristic of the extracts decreased. For an increase in antioxidant activity, the average analyzed process time was more favorable, as was the average biomass/water ratio (0.050 g/mL). In addition, it was noted that the highest microwave power analyzed led to extracts with higher antioxidant potential.

Compared to the assessment of TFC and TAA, a completely different trend was observed for the analysis of total reducing sugars in the extracts. The models generated indicate the parameters at which there was a sharp decrease. This was the case for a biomass-to-solvent ratio value of 0.050 g/mL. Increasing the exposure time of the samples to microwaves led to an increase in RSC levels. When analyzing the effect of microwave power, it was shown that for 550 and 650 W, similar concentrations of reducing sugars occurred. Increasing this parameter only, up to the maximum analyzed in the experiment, resulted in increased differences in RSC in the extracts (Figure 7).

3.2. Multi-Criteria Optimization of Microwave-Assisted Aqueous Extraction Process

The generated models in the form of multivariate regression equations, supported by the interpolation of multivariate polynomial equations, were then used in multi-criteria (multi-objective) optimization procedures. Thus, by combining all equations, it was possible to create a so-called global model for multi-objective optimization, which made it possible to predict multiple output signals (TPC, TFC, TAA, RSC) as a function of the input process parameters (x₁, x₂, x₃). The predictive outputs (criteria) indicate the possibility of global insights into the entire extraction process efficiency domain under study, which was expressed in terms of maximizing the values of the individual criteria. Figure 8 and Figure 9 show Pareto fronts in the two-dimensional and three-dimensional decision criteria space (after normalization for the maximized criteria, 0 is the best case scenario). Due to the demonstrated complexity, the analysis of the research problem required visualization of the results of multi-objective optimization (Figure 10) with representation of the Pareto-optimal solution sets in the space of the decision variables x₁ (sample/solvent ratio), x₂ (microwave power), and x₃ (time). The analysis of the Pareto fronts showed that the edge is a multiconsistent set. It should be emphasized that the process parameters of microwave-assisted aqueous extraction (x₁, x₂ and x₃) simultaneously influenced the objective function of the identified domain. Thus, the mathematical model of the four-objective optimization problem, determining the extraction process, focused on finding parameters such that x = (x₁^opt, x₂^opt, x₃^opt) in the analyzed domain.

In the multi-object Pareto front shown in Figure 8, POS, obtained as a result of optimization in the space of decision variables (microwave-assisted extraction process parameters), shows the multiplicity of Pareto optimal solutions (possible scenarios for decision-making). This therefore indicates the need to consider the problem of maximizing the bioactive compounds in extracts by designing them in conjunction with a real-world situation (process analysis of optimization results using the decision maker). Therefore, the decision maker can choose the parameters for microwave-assisted aqueous extraction, based on knowledge and preference, as well as on practical technical and engineering requirements. In such a decision-making process, the set of Pareto optimal solutions (against dominated solutions) presented in a three-dimensional space of decision variables is of great help. It is proven that there is a relatively large area of non-dominated solutions. It was shown that for maximizing the four analyzed quality criteria of Levisticum officinale extracts, a number of options can be chosen. First of all, the boundary conditions of the process itself can be applied, i.e., increasing the extraction process time, as well as increasing the microwave power and the biomass/water ratio. The second option indicates that achieving the objective function (maximizing the criteria) with a low ratio of lovage roots to the extractant agent assumes increased microwave power or exposure time. Increasing the biomass/solvent ratio, on the other hand, allows for a decrease in microwave power and a shortening of the procedure to achieve satisfactory levels of bioactive compounds. Moving further into the three-dimensional space of Pareto optimal solutions, it can also be seen that the use of medium microwave power and medium biomass/solvent ratios can reduce the time of the entire extraction process (

Table 2. Optimal solutions from the Pareto front for decision variables.

x1 (Sample/Solvent Ratio)	x2 (Microwave Power)	x3 (Time)	x1 (Sample/Solvent Ratio)	x2 (Microwave Power)	x3 (Time)
0.0250	550.0000	30.0000	0.0607	721.4286	34.2857
0.0250	550.0000	34.2857	0.0607	735.7143	30.0000
0.0250	550.0000	38.5714	0.0607	735.7143	34.2857
0.0250	550.0000	42.8571	0.0607	735.7143	38.5714
0.0250	550.0000	47.1429	0.0607	735.7143	42.8571
0.0250	550.0000	51.4286	0.0607	735.7143	60.0000
0.0250	564.2857	30.0000	0.0607	735.7143	64.2857
0.0250	564.2857	34.2857	0.0607	735.7143	68.5714
0.0250	564.2857	38.5714	0.0607	735.7143	72.8571
0.0250	564.2857	42.8571	0.0607	735.7143	81.4286
0.0250	578.5714	30.0000	0.0607	735.7143	85.7143
0.0250	578.5714	34.2857	0.0607	735.7143	90.0000
0.0250	578.5714	38.5714	0.0607	750.0000	30.0000
0.0250	592.8571	30.0000	0.0607	750.0000	34.2857
0.0250	735.7143	38.5714	0.0607	750.0000	38.5714
0.0250	735.7143	42.8571	0.0607	750.0000	42.8571
0.0250	735.7143	47.1429	0.0607	750.0000	47.1429
0.0250	735.7143	51.4286	0.0607	750.0000	51.4286
0.0250	735.7143	55.7143	0.0607	750.0000	55.7143
0.0250	735.7143	60.0000	0.0607	750.0000	60.0000
0.0250	750.0000	38.5714	0.0607	750.0000	64.2857
0.0250	750.0000	42.8571	0.0607	750.0000	68.5714
0.0250	750.0000	47.1429	0.0607	750.0000	72.8571
0.0250	750.0000	51.4286	0.0607	750.0000	77.1429
0.0250	750.0000	55.7143	0.0607	750.0000	81.4286
0.0250	750.0000	60.0000	0.0607	750.0000	85.7143
0.0250	750.0000	64.2857	0.0607	750.0000	90.0000
0.0250	750.0000	68.5714	0.0643	550.0000	30.0000
0.0250	750.0000	72.8571	0.0643	550.0000	34.2857
0.0250	750.0000	77.1429	0.0643	550.0000	38.5714
0.0250	750.0000	81.4286	0.0643	550.0000	42.8571
0.0250	750.0000	85.7143	0.0643	550.0000	47.1429
0.0250	750.0000	90.0000	0.0643	550.0000	51.4286
0.0286	550.0000	30.0000	0.0643	564.2857	30.0000
0.0286	550.0000	34.2857	0.0643	578.5714	30.0000
0.0286	550.0000	38.5714	0.0643	592.8571	30.0000
0.0286	550.0000	42.8571	0.0643	607.1429	30.0000
0.0286	564.2857	30.0000	0.0643	621.4286	30.0000
0.0286	564.2857	34.2857	0.0643	635.7143	30.0000
0.0286	564.2857	38.5714	0.0643	650.0000	30.0000
0.0286	564.2857	42.8571	0.0643	664.2857	30.0000
0.0286	578.5714	30.0000	0.0643	678.5714	30.0000
0.0286	578.5714	34.2857	0.0643	692.8571	30.0000
0.0286	578.5714	38.5714	0.0643	707.1429	30.0000
0.0286	750.0000	51.4286	0.0643	721.4286	30.0000
0.0286	750.0000	55.7143	0.0643	721.4286	34.2857
0.0286	750.0000	60.0000	0.0643	721.4286	38.5714
0.0286	750.0000	64.2857	0.0643	735.7143	34.2857
0.0286	750.0000	68.5714	0.0643	735.7143	42.8571
0.0286	750.0000	72.8571	0.0643	735.7143	47.1429
0.0286	750.0000	77.1429	0.0643	735.7143	51.4286
0.0286	750.0000	81.4286	0.0643	735.7143	55.7143
0.0286	750.0000	85.7143	0.0643	735.7143	60.0000
0.0286	750.0000	90.0000	0.0643	735.7143	64.2857
0.0321	564.2857	30.0000	0.0643	735.7143	68.5714
0.0321	578.5714	30.0000	0.0643	735.7143	72.8571
0.0321	750.0000	51.4286	0.0643	735.7143	85.7143
0.0321	750.0000	55.7143	0.0643	735.7143	90.0000
0.0321	750.0000	60.0000	0.0643	750.0000	30.0000
0.0321	750.0000	64.2857	0.0643	750.0000	34.2857
0.0321	750.0000	68.5714	0.0643	750.0000	38.5714
0.0321	750.0000	72.8571	0.0643	750.0000	42.8571
0.0321	750.0000	77.1429	0.0643	750.0000	47.1429
0.0321	750.0000	81.4286	0.0643	750.0000	51.4286
0.0321	750.0000	85.7143	0.0643	750.0000	55.7143
0.0321	750.0000	90.0000	0.0643	750.0000	60.0000
0.0357	750.0000	55.7143	0.0643	750.0000	64.2857
0.0357	750.0000	60.0000	0.0643	750.0000	68.5714
0.0357	750.0000	64.2857	0.0643	750.0000	72.8571
0.0357	750.0000	68.5714	0.0643	750.0000	77.1429
0.0357	750.0000	72.8571	0.0643	750.0000	81.4286
0.0357	750.0000	77.1429	0.0643	750.0000	85.7143
0.0357	750.0000	81.4286	0.0643	750.0000	90.0000
0.0357	750.0000	85.7143	0.0679	550.0000	30.0000
0.0357	750.0000	90.0000	0.0679	550.0000	34.2857
0.0393	750.0000	55.7143	0.0679	550.0000	38.5714
0.0393	750.0000	60.0000	0.0679	550.0000	42.8571
0.0393	750.0000	64.2857	0.0679	550.0000	47.1429
0.0393	750.0000	68.5714	0.0679	550.0000	51.4286
0.0393	750.0000	72.8571	0.0679	564.2857	30.0000
0.0393	750.0000	77.1429	0.0679	578.5714	30.0000
0.0393	750.0000	81.4286	0.0679	592.8571	30.0000
0.0393	750.0000	85.7143	0.0679	607.1429	30.0000
0.0393	750.0000	90.0000	0.0679	621.4286	30.0000
0.0429	735.7143	64.2857	0.0679	635.7143	30.0000
0.0429	750.0000	51.4286	0.0679	650.0000	30.0000
0.0429	750.0000	55.7143	0.0679	664.2857	30.0000
0.0429	750.0000	60.0000	0.0679	678.5714	30.0000
0.0429	750.0000	64.2857	0.0679	692.8571	30.0000
0.0429	750.0000	68.5714	0.0679	707.1429	30.0000
0.0429	750.0000	72.8571	0.0679	721.4286	30.0000
0.0429	750.0000	77.1429	0.0679	735.7143	30.0000
0.0429	750.0000	81.4286	0.0679	735.7143	34.2857
0.0429	750.0000	85.7143	0.0679	735.7143	38.5714
0.0429	750.0000	90.0000	0.0679	735.7143	42.8571
0.0464	735.7143	55.7143	0.0679	735.7143	47.1429
0.0464	750.0000	42.8571	0.0679	735.7143	51.4286
0.0464	750.0000	47.1429	0.0679	735.7143	55.7143
0.0464	750.0000	51.4286	0.0679	735.7143	60.0000
0.0464	750.0000	55.7143	0.0679	735.7143	64.2857
0.0464	750.0000	60.0000	0.0679	735.7143	68.5714
0.0464	750.0000	64.2857	0.0679	735.7143	72.8571
0.0464	750.0000	68.5714	0.0679	750.0000	30.0000
0.0464	750.0000	72.8571	0.0679	750.0000	34.2857
0.0464	750.0000	77.1429	0.0679	750.0000	38.5714
0.0464	750.0000	81.4286	0.0679	750.0000	42.8571
0.0464	750.0000	85.7143	0.0679	750.0000	47.1429
0.0464	750.0000	90.0000	0.0679	750.0000	51.4286
0.0500	550.0000	34.2857	0.0679	750.0000	55.7143
0.0500	550.0000	38.5714	0.0679	750.0000	60.0000
0.0500	564.2857	30.0000	0.0679	750.0000	64.2857
0.0500	735.7143	38.5714	0.0679	750.0000	68.5714
0.0500	735.7143	47.1429	0.0679	750.0000	72.8571
0.0500	735.7143	51.4286	0.0679	750.0000	77.1429
0.0500	735.7143	55.7143	0.0679	750.0000	81.4286
0.0500	735.7143	60.0000	0.0679	750.0000	85.7143

). And this is where the flexibility of the controllability of the microwave-assisted aqueous extraction process comes in.

Due to the determined number of Pareto optimal solutions, an approach related to the introduction of preferences in the optimization procedure was applied in the next step. The Pareto set reduction method was used, and set navigation was carried out using an a priori method, based on the preference of the decision-making process to direct the finding of optimal solutions to the preferred region, through different weighting of criteria and interest in alternative solution scenarios. The effects of this solution set reduction approach are shown in Figure 11.

Reducing the solutions from the Pareto fronts and the so-called smart Pareto approach yielded a subset of optimal solutions (preferred solutions). Assigning weights to the criteria allowed the first three quality criteria of the extracts to be given greater importance (

Table 3. Pareto front solution reduction—subsets of optimal solutions (smart Pareto) for decision variables.

x1 (Sample/Solvent Ratio)	x2 (Microwave Power)	x2 (Time)	x1 (Sample/Solvent Ratio)	x2 (Microwave Power)	x3 (Time)
0.0536	750	77.1429	0.0607	750	85.7143
0.0536	750	81.4286	0.0643	750	64.2857
0.0536	750	85.7143	0.0643	750	68.5714
0.0571	750	72.8571	0.0643	750	72.8571
0.0571	750	77.1429	0.0643	750	77.1429
0.0571	750	81.4286	0.0643	750	81.4286
0.0571	750	85.7143	0.0643	750	85.7143
0.0607	750	68.5714	0.0679	750	64.2857
0.0607	750	72.8571	0.0679	750	68.5714
0.0607	750	77.1429	0.0679	750	72.8571
0.0607	750	81.4286	0.0679	750	77.1429

). The optimal subsets showed that for satisfactory levels of biologically active compounds, aqueous extraction should be carried out at a maximum microwave power of 750 W. Preferred solutions were obtained for Levisticum officinale biomass/solvent ratios ranging from 0.0536 g/mL to 0.0679 g/mL. In contrast, the preferred optimum running time for microwave-assisted aqueous extraction was in the range of 64.2857 to 85.7143 s. Thus, for the maximization of phenolic compounds, flavonoids, and antioxidant potential, it is not indicated that extraction should be conducted at maximum process parameters.

The next proposed step in the search for optimal solutions was a post-Pareto analysis, involving the determination of the distance of points from the front end to the ideal “unattainable” Utopia point, based on the decision maker’s additional input in deciding which compromise solutions would be accepted. This approach allowed the Pareto optimal set to be narrowed down, while allowing the decision maker to have access to a set of solutions with a practical dimension. The sets of compromise solutions as a function of the two decision variables are shown in Figure 12, while for a more complete visualization, Figure 13 shows the sets of compromise solutions in the three-dimensional space of all analyzed variables/parameters of the extraction process.

Analysis of the trade-off solutions in the space of decision variables shows that they occur in two subsets (Figure 13).

The set of Pareto compromise solutions is shown in

Table 4. The set of Pareto compromise solutions for the MAE extraction.

x1 (Sample/Solvent Ratio)	x2 (Microwave Power)	x3 (Time)	x1 (Sample/Solvent Ratio)	x2 (Microwave Power)	x3 (Time)
0.0357	750.0000	85.7143	0.0643	564.2857	30.0000
0.0357	750.0000	90.0000	0.0643	564.2857	34.2857
0.0393	750.0000	72.8571	0.0643	564.2857	38.5714
0.0393	750.0000	77.1429	0.0643	578.5714	30.0000
0.0393	750.0000	81.4286	0.0643	578.5714	34.2857
0.0393	750.0000	85.7143	0.0643	578.5714	38.5714
0.0393	750.0000	90.0000	0.0643	592.8571	30.0000
0.0429	750.0000	68.5714	0.0643	721.4286	47.1429
0.0429	750.0000	72.8571	0.0643	721.4286	51.4286
0.0429	750.0000	77.1429	0.0643	721.4286	55.7143
0.0429	750.0000	81.4286	0.0643	735.7143	42.8571
0.0429	750.0000	85.7143	0.0643	735.7143	47.1429
0.0429	750.0000	90.0000	0.0643	735.7143	51.4286
0.0464	550.0000	30.0000	0.0643	735.7143	55.7143
0.0464	550.0000	34.2857	0.0643	735.7143	60.0000
0.0464	750.0000	64.2857	0.0643	750.0000	38.5714
0.0464	750.0000	68.5714	0.0643	750.0000	42.8571
0.0464	750.0000	72.8571	0.0643	750.0000	47.1429
0.0464	750.0000	77.1429	0.0643	750.0000	51.4286
0.0464	750.0000	81.4286	0.0643	750.0000	55.7143
0.0464	750.0000	85.7143	0.0643	750.0000	60.0000
0.0500	550.0000	30.0000	0.0643	750.0000	64.2857
0.0500	550.0000	34.2857	0.0679	550.0000	30.0000
0.0500	550.0000	38.5714	0.0679	550.0000	34.2857
0.0500	564.2857	30.0000	0.0679	550.0000	38.5714
0.0500	750.0000	60.0000	0.0679	564.2857	30.0000
0.0500	750.0000	64.2857	0.0679	564.2857	34.2857
0.0500	750.0000	68.5714	0.0679	564.2857	38.5714
0.0500	750.0000	72.8571	0.0679	578.5714	30.0000
0.0500	750.0000	77.1429	0.0679	578.5714	34.2857
0.0500	750.0000	81.4286	0.0679	721.4286	42.8571
0.0536	550.0000	30.0000	0.0679	721.4286	47.1429
0.0536	550.0000	34.2857	0.0679	721.4286	51.4286
0.0536	550.0000	38.5714	0.0679	721.4286	55.7143
0.0536	564.2857	30.0000	0.0679	735.7143	38.5714
0.0536	564.2857	34.2857	0.0679	735.7143	42.8571
0.0536	564.2857	38.5714	0.0679	735.7143	47.1429
0.0536	750.0000	55.7143	0.0679	735.7143	51.4286
0.0536	750.0000	60.0000	0.0679	735.7143	55.7143
0.0536	750.0000	64.2857	0.0679	735.7143	60.0000
0.0536	750.0000	68.5714	0.0679	750.0000	34.2857
0.0536	750.0000	72.8571	0.0679	750.0000	38.5714
0.0571	550.0000	30.0000	0.0679	750.0000	42.8571
0.0571	550.0000	34.2857	0.0679	750.0000	47.1429
0.0571	550.0000	38.5714	0.0679	750.0000	51.4286
0.0571	550.0000	42.8571	0.0679	750.0000	55.7143
0.0571	564.2857	30.0000	0.0679	750.0000	60.0000
0.0571	564.2857	34.2857	0.0679	750.0000	64.2857
0.0571	564.2857	38.5714	0.0714	550.0000	30.0000
0.0571	578.5714	30.0000	0.0714	550.0000	34.2857
0.0571	578.5714	34.2857	0.0714	564.2857	30.0000
0.0571	735.7143	55.7143	0.0714	564.2857	34.2857
0.0571	735.7143	60.0000	0.0714	721.4286	38.5714
0.0571	750.0000	51.4286	0.0714	721.4286	42.8571
0.0571	750.0000	55.7143	0.0714	721.4286	47.1429
0.0571	750.0000	60.0000	0.0714	721.4286	51.4286
0.0571	750.0000	64.2857	0.0714	735.7143	38.5714
0.0571	750.0000	68.5714	0.0714	735.7143	42.8571
0.0607	550.0000	30.0000	0.0714	735.7143	47.1429
0.0607	550.0000	34.2857	0.0714	735.7143	51.4286
0.0607	550.0000	38.5714	0.0714	735.7143	55.7143
0.0607	550.0000	42.8571	0.0714	735.7143	60.0000
0.0607	564.2857	30.0000	0.0714	750.0000	34.2857
0.0607	564.2857	34.2857	0.0714	750.0000	38.5714
0.0607	564.2857	38.5714	0.0714	750.0000	42.8571
0.0607	578.5714	30.0000	0.0714	750.0000	47.1429
0.0607	578.5714	34.2857	0.0714	750.0000	51.4286
0.0607	578.5714	38.5714	0.0714	750.0000	55.7143
0.0607	735.7143	47.1429	0.0714	750.0000	60.0000
0.0607	735.7143	51.4286	0.0714	750.0000	64.2857
0.0607	735.7143	55.7143	0.0750	735.7143	38.5714
0.0607	735.7143	60.0000	0.0750	735.7143	42.8571
0.0607	750.0000	42.8571	0.0750	735.7143	47.1429
0.0607	750.0000	47.1429	0.0750	735.7143	51.4286
0.0607	750.0000	51.4286	0.0750	750.0000	34.2857
0.0607	750.0000	55.7143	0.0750	750.0000	38.5714
0.0607	750.0000	60.0000	0.0750	750.0000	42.8571
0.0607	750.0000	64.2857	0.0750	750.0000	47.1429
0.0607	750.0000	68.5714	0.0750	750.0000	51.4286
0.0643	550.0000	30.0000	0.0750	750.0000	55.7143
0.0643	550.0000	34.2857	0.0750	750.0000	60.0000
0.0643	550.0000	38.5714

. By minimizing the distance of non-dominated solutions from the Utopia point, it was shown that for simultaneous maximization of the decision criteria, the extraction process can be controlled over certain ranges of decision variables.

To obtain extracts of satisfactory composition, a scenario in which a reduced biomass/water ratio (from 0.0357 to 0.0464 g/mL) can be used, but the highest microwave power must be employed. Increasing the biomass/water ratio to 0.0571 g/mL, on the other hand, allows the microwave power to be lowered significantly, while reducing the time of the process itself.

To evaluate the two procedures, Figure 14 compares the preferred solutions from the Pareto front against the compromise solutions. It should be emphasized that at this stage, it is up to the decision maker to decide which analysis is of greater practical relevance for the design and control of the microwave-assisted extraction process.

Theoretically, the compromise solutions, determined using an acceptable distance from the Utopia point, form concrete sets in which the decision maker can move. In the 3D visualization in the space of all decision variables, the elements of this set are equal compromise solutions. However, this can sometimes lead to a problem in decision making during the actual process. Often, there is a need to select and identify one specific and preferred solution from the set of compromise solutions. Thus, out of the set of compromise solutions, one was identified whose distance from the Utopia point was the smallest among all the solutions analyzed. Such an optimal compromise solution was identified as the point in the space of decision variables with coordinates x₁ = 0.0643 g/mL, x₂ = 550 W, and x₃ = 30 s (thus, a so-called “super” compromise solution was identified).

4. Discussion

Microwave-assisted extraction (MAE) is a process that is currently receiving considerable attention in the literature. This is due to the fact that this method allows for a significant reduction in processing time and extractant agent consumption with respect to conventional extraction [12]. In addition, it allows the principles and objectives of green chemistry to be realized, due to the possibility of using water as an eco-friendly solvent. The interest in microwave-assisted extraction is largely due to the possibility of improving the efficiency of the extraction of bioactive compounds from plant biomass, including compounds with antioxidant activity. Therefore, the design and optimization of extraction processes is becoming increasingly important. This is because it is of particular importance not only in preventing the loss of bioactive compounds, which are sensitive to process parameters, but also in minimizing the cost intensity of the extraction procedure itself [37]. In our research, the process variables that determined the efficiency of bioactive compound extraction were extraction time, microwave power, and the ratio of plant biomass to the solvent. It was shown that for increased yields of phenolic compounds and reducing sugars, an increased biomass ratio of Levisticum officianle roots to water was more beneficial.

On the other hand, the ratio had a different effect on the flavonoid levels and antioxidant potential of the extracts. It was shown that there was a decrease in the content of these compounds in the extracts when the central analyzed value of this ratio was exceeded. Kim and Lim [38] also studied the effect of the ratio of Citrus unshiu pomace to solvent on the extraction efficiency of flavonoids. The amount of these bioactive compounds increased with an increase in this extraction parameter. However, the researchers did not observe statistically significant differences. Admittedly, according to Iglesias-Carres et al. [39], a high biomass/solvent ratio leads to the improved extraction efficiency of bioactive compounds, which the researchers explain by an increased concentration difference at the sample/extractant interface. However, as Assefa et al. [40] pointed out, conducting extraction with an increased biomass ratio is economically unjustifiable, as it involves, firstly, obtaining negligible differences in the levels of bioactive compounds and secondly, increased energy consumption in the subsequent concentration steps of the extracts produced [40]. A study by Hayat et al. [41] showed that the performance of an extraction process using banana peels was drastically reduced when the procedure was conducted at increased biomass/solvent ratios. According to the authors, an excessive increase in the sample/solvent ratio leads to a decrease in the concentration of phenolic compounds and antioxidant potential in DPPH and FRAP assays. Hayat et al. [41] hypothesized that the observed trends may be due to the swelling process of the plant material, which in turn leads to an increase in the contact zone between the biological matrix and the extractant agent [42]. Dahmoune et al. [17] emphasized that for the design of industrial-scale extraction, preliminary experimental studies are needed, conducted with a view to maximizing the extraction efficiency of bioactive compounds in terms of minimizing the solvents and plant matrices used [17]. Taking this into account, Kim and Lim [38] put forward the proposal that the procedure for optimizing microwave-assisted extraction should include the selection of an appropriate range of the sample to solvent ratio.

The research on the extraction of active compounds from the roots of Levisticum officinale also showed the effect of process time on the levels of phenolic compounds, flavonoids, sugars, and antioxidant potential. It was found that increasing the time resulted in an increase in the pool of these compounds, although increasing the time no longer resulted in such large increases. However, in the case of the antioxidant potential, assessed by the DPPH test, there was a decrease in this parameter when a certain time limit was exceeded. This is confirmed by the results obtained by Kim and Lim [38], who found that the extraction efficiency of flavonoids from Citrus unshiu pomace reached a maximum level at a certain time, after which there was no longer a significant change in this parameter. Similar observations were also reached by Mokrani and Madani [43], who evaluated the effect of time on the extraction efficiency of phenolic compounds and the antioxidant capacity of peach fruit. According to the researchers, the observed phenomenon is a direct result of Fick’s second law of diffusion, according to which, after a certain amount of time, there will be a final equilibrium between the plant biomass and the solvent of the concentrations in the reaction system, [43]. Vu et al. [42] emphasized that time is the extraction parameter of key importance, and in the case of microwave extraction, this impact is even greater. Therefore, an important optimization task is pointed out to determine the appropriate time range for conducting the extraction. Dahmoune et al. [17] indicate that extending the extraction time beyond the optimal range may lead to a decrease in the efficiency of extracting bioactive components from the plant matrix due to the fact that an uncontrolled increase in temperature and thermal degradation of antioxidant compounds may occur.

The last parameter of the microwave-assisted extraction process optimized in this research was the power of the magnetron. Increasing microwave power led to increased levels of bioactive compounds. However, for the content of phenolic compounds and flavonoids, increasing the microwave power from 650 to 750 W no longer resulted in significant differences. Research by Kheyar et al. [44], which focused on optimizing microwave-assisted extraction for maximizing the total pool of phenolic compounds from Moringa oleifera leaves, confirmed that microwave power determined the efficiency of the process. However, for the optimal power of 626.53 W, the extraction time was prolonged compared to that noted in studies on Levisticum officinale.

In contrast, a study by Sai-Ut et al. [45] found that the optimal microwave power for the extraction of polyphenols from Careya sphaerica Roxb. was 1000 W. On the other hand, this required an increased ratio of plant biomass to solvent. The positive effect of using microwaves in the extraction process is pointed out by Kheyar et al. [44] who stated that the content of polyphenols increased with increasing microwave power, reaching a maximum at 500 W. Increasing the microwave power to 1000 W resulted in a decrease in the polyphenol content of the extract. The reason for this situation may be that microwaves affect the plant material too intensively, causing structural changes that negatively affect the availability of polyphenols or the loss of their stability. High microwave power can also stimulate reactions that reduce the availability of bioactive compounds. Moreover, Mandal et al. [46] confirmed that microwave energy is a determinant of the extraction efficiency of phenolic compounds. However, the researchers emphasized that increasing the microwave power may lead to disruption of the dynamic structure of the sample and degradation of the bioactive compounds [46]. In addition, unjustified increases in microwave energy no longer lead to a significant increase in the extraction efficiency of active compounds and are associated with higher economic expenses [42].

Thus, as many researchers point out, there is a need not only to design the extraction process, but also to optimize its efficiency. This is particularly relevant for microwave-assisted extraction, as it can ultimately reduce the energy intensity of the process. Therefore, optimization problems in real processes are characterized by multiple, sometimes conflicting objectives. It should be emphasized that the multi-objective optimization procedures for microwave-assisted extraction proposed in this paper are not only a search for a set of solutions (process parameters), but also a decision-making process based on the knowledge, experience, and preferences of the decision maker. Only by integrating computer methods with the decision maker’s position will it be possible to identify a set or region of optimal solutions to control the extraction process. The results of the optimization procedures presented in this work will allow the decision maker to make a posteriori decisions. In such a case, sets of Pareto optimal, preferred, and compromise solutions generated without the decision maker’s preferences can be provided to him to make a decision based on the most preferred options among the alternatives [47]. Therefore, the method developed in this work allows for the creation of a sequential process in which the decision maker reaches decisions about the parameters of the extraction procedure, knowing that he is choosing from non-dominated solutions, and the optimization of each analyzed criterion corresponds to the maximum value of this criterion. However, if in the decision-making process there is a need to give greater importance to individual criteria, the proposed procedure also makes this possible by indicating preferred solutions [47,48].

5. Conclusions

The root biomass of Levisticum officinale is rich in bioactive compounds with high antioxidant potential. It has also been shown that microwave-assisted water extraction is a suitable method for ecologically obtaining phytochemicals from lovage biomass. For industrial applications and the improvement of such an extraction procedure, mathematical models with the correct predictive ability were created and used in optimization procedures and in the forecasting of process parameters. Sets of Pareto optimal, compromise, and preferred solutions were indicated, which will allow for maximizing the efficiency of the extraction of bioactive compounds from plant biomass. Optimized processing conditions will not only improve the extraction process, but are also necessary to increase the scale of ecological production of compounds with antioxidant potential intended for various industries, including applications in the fields of pharmacy, foods, and agronomy. The multi-objective optimization procedures proposed in this work will not only enable the search for a set of optimal solutions (process parameters), but will also facilitate the decision-making process, based on the knowledge, experience, and preferences of the decision maker. In the optimal subsets, it was shown that for a satisfactory level of bioactive compounds, extraction should be carried out at a maximum microwave power of 750 W. The preferred solutions were obtained for the ratio of Levisticum officinale root biomass to water in the range of 0.0536 g/mL to 0.0679 g/mL. The preferred optimal time for microwave-assisted water extraction ranged from 64.2857 to 85.7143 s. The conducted research and multi-criteria optimization methods indicate the need for further research in this area to identify a greater role for the decision maker and to increase the scale of microwave-assisted extraction for industrial applications.