Piezoelectric Actuators in Smart Engineering Structures Using Robust Control
Abstract
:1. Introduction
2. Materials and Methods
2.1. Piezoelectric Materials
2.2. Smart Structures
2.3. Motion Equation of the Intelligent Structure
2.4. Modeling
2.5. Robustness Issues
M = M0(I + mpI2n×2nδM)
D0 = 0.0005K0 + 0.0005M0
D0 + 0.0005[K0kpI2n×2nδK + M0mpI2n×2nδM]
3. Results and Discussion
3.1. Results
3.2. Discussion
- System Modeling: The first step is to develop an accurate mathematical model of the smart structure dynamics, including the piezoelectric actuator, structural components, sensors, and external disturbances. The model captured the electromechanical coupling of the piezoelectric material, structural dynamics, and feedback loops.
- Uncertainty Description: H∞ control addresses uncertainties in a system model. These uncertainties can arise from modeling errors, parameter variations, environmental changes, or disturbances. It is essential to quantify these uncertainties and represent them within a control design framework.
- Performance Specifications: Performance criteria for a smart structure system are defined. This includes stability requirements, tracking accuracy, disturbance rejection, bandwidth limitations, and robustness margins. These specifications guide the design of the H∞ controller to ensure that the system satisfies the desired performance objectives under various conditions.
- Controller Design: Utilize H∞ control synthesis techniques to design a robust controller that minimizes the effects of uncertainties and disturbances on system performance while satisfying performance specifications. H∞ controllers are typically designed based on a structured singular value (μ) optimization framework that aims to minimize the worst-case sensitivity of the system.
- Controller Implementation: The designed H∞ controller is implemented on the smart structure system and integrated with the piezoelectric actuator control loop. This involves tuning controller parameters, setting up feedback loops, and interfacing sensors and actuators to achieve the desired control behavior.
4. Conclusions
- Modeling Intelligent Structures for Control in Oscillation Suppression
- We developed a mathematical model for intelligent structures that allows for the effective control of oscillations.
- Handling Uncertainties in Dynamic Loading.
- Our approach addresses the uncertainties arising from dynamic loading conditions and ensures robust control performance.
- Measurement Noise management
- We accounted for measurement noise in the system, thereby enhancing the accuracy and reliability of our control strategy.
- Selection of Optimal Weights for Suppression of Oscillation
- Through appropriate weighting functions, we achieved the complete suppression of oscillations and optimized the control performance.
- Analysis of Time and Frequency Domains
- Our results are presented and analyzed comprehensively in both the time and frequency domains, providing a thorough understanding of control performance.
- Incorporation of Uncertainties in the Mathematical Model of the Structure
- Uncertainties were introduced into the mathematical model of the structure, making our approach more robust and adaptable to real-world conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| M: | Mass matrix | ψi(t): | Displacement deflection |
| K: | Stiffness matrix | x(t): | The state vector of our system |
| D: | Viscous damping matrix | y(t): | Output vector of our system |
| fe(t) fm(t) | Piezoelectric force External mechanical force | d31: | Piezoelectric constant |
| n: | Number of nodes in finite element formulation | Cp, Co Kf | Piezoelectric constant |
| u(t): | Control voltages of actuators (control vector) | K(s): | Hinfinity Controller of the system |
| Fe: | Matrix with piezoelectric constant | E | The young modulus of the beam |
| wi(t): | Rotation deflection | P: | Augment plant of the smart system |
| μ: | Singular value | e(t): | The error of the system |
| d(t): | Disturbances of the system | n(t): | Noise of the system |
| A, B | Matrices of our system | D, G-K: | D–K interaction in the frequency domain |
| w | Inputs of the smart systems (external disturbance, noise) | z | Outputs of the smart system (control vector, output vector) |
| Wn: | The noise weight for H-infinity control | Wu: | The control weight for Hinfinity control |
| Wd: | The disturbance weight for H-infinity control | V(t)
d(t) | Wind speed External disturbance of the smart system |
| Δ: | The uncertainty of the system | δM t | The uncertainty terms for the mass matrix |
| δκ | The uncertainty terms for the stiffness matrix | kp, mp: | Numerical constant from zero to one |
| p | Density of the beam | W | Width of the smart beam |
| h | Thickness of the smart beam | hp, hs | Width of pzt patches |
References
- Tzou, H.S.; Gabbert, U. Structronics—A New Discipline and Its Challenging Issues. In Fortschritt-Berichte VDI, Smart Mechanical Systems—Adaptronics, Reihe; Verein Deutscher Ingenieure: Düsseldorf, Germany, 1997; Volume 11, pp. 245–250. [Google Scholar]
- Guran, A.; Tzou, H.-S.; Anderson, G.L.; Natori, M.; Gabbert, U.; Tani, J.; Breitbach, E. Structronic Systems: Smart Structures, Devices and Systems; World Scientific: Singapore, 1998; Volume 4, ISBN 978-981-02-2652-7. [Google Scholar]
- Tzou, H.S.; Anderson, G.L. Intelligent Structural Systems; Springer: Dordrecht, The Netherlands, 1992; ISBN 978-94-017-1903-2. [Google Scholar]
- Gabbert, U.; Tzou, H.S. IUTAM Symposium on Smart Structures and Structronic Systems. In Proceedings of the IUTAM Symposium, Magdeburg, Germany, 26–29 September 2000; Kluwer: Dordrecht, The Netherlands; Boston, MA, USA; London, UK, 2001. [Google Scholar]
- Tzou, H.S.; Natori, M.C. Piezoelectric Materials and Continua; Elsevier: Oxford, UK, 2001; pp. 1011–1018. ISBN 978-0-12-227085-7. [Google Scholar]
- Cady, W.G. Piezoelectricity: An Introduction to the Theory and Applications of Electromechanical Phenomena in Crystals; Dover Publication: New York, NY, USA, 1964. [Google Scholar]
- Tzou, H.S.; Bao, Y. A theory on Anisotropic Piezothermoelastic Shell Laminates with Sensor/Actuator Applications. J. Sound Vib. 1995, 184, 453–473. [Google Scholar] [CrossRef]
- Bikas, H.; Stavropoulos, P.; Chryssolouris, G. Additive Manufacturing Methods and Modelling Approaches: A Critical Review. Int. J. Adv. Manuf. Technol. 2016, 83, 389–405. [Google Scholar] [CrossRef]
- Stavropoulos, P.; Chantzis, D.; Doukas, C.; Papacharalampopoulos, A.; Chryssolouris, G. Monitoring and Control of Manufacturing Processes: A Review. Procedia CIRP 2013, 8, 421–425. [Google Scholar] [CrossRef]
- Moutsopoulou, A.; Stavroulakis, G.E.; Petousis, M.; Vidakis, N.; Pouliezos, A. Smart Structures Innovations Using Robust Control Methods. Appl. Mech. 2023, 4, 856–869. [Google Scholar] [CrossRef]
- Vidakis, N.; Petousis, M.; Mountakis, N.; Moutsopoulou, A.; Karapidakis, E. Energy Consumption vs. Tensile Strength of Poly [Methyl Methacrylate] in Material Extrusion 3D Printing: The Impact of Six Control Settings. Polymers 2023, 15, 845. [Google Scholar] [CrossRef] [PubMed]
- Vidakis, N.; Petousis, M.; Mountakis, N.; Papadakis, V.; Moutsopoulou, A. Mechanical Strength Predictability of Full Factorial, Taguchi, and Box Behnken Designs: Optimization of Thermal Settings and Cellulose Nanofibers Content in PA12 for MEX AM. J. Mech. Behav. Biomed. Mater. 2023, 142, 105846. [Google Scholar] [CrossRef] [PubMed]
- Cen, S.; Soh, A.-K.; Long, Y.-Q.; Yao, Z.-H. A New 4-Node Quadrilateral FE Model with Variable Electrical Degrees of Freedom for the Analysis of Piezoelectric Laminated Composite Plates. Compos. Struct. 2002, 58, 583–599. [Google Scholar] [CrossRef]
- Yang, S.M.; Lee, Y.J. Optimization of Noncollocated Sensor/Actuator Location and Feedback Gain in Control Systems. Smart Mater. Struct. 1993, 2, 96. [Google Scholar] [CrossRef]
- Ramesh Kumar, K.; Narayanan, S. Active Vibration Control of Beams with Optimal Placement of Piezoelectric Sensor/Actuator Pairs. Smart Mater. Struct. 2008, 17, 55008. [Google Scholar] [CrossRef]
- Hanagud, S.; Obal, M.W.; Calise, A.J. Optimal Vibration Control by the Use of Piezoceramic Sensors and Actuators. J. Guid. Control Dyn. 1992, 15, 1199–1206. [Google Scholar] [CrossRef]
- Song, G.; Sethi, V.; Li, H.-N. Vibration Control of Civil Structures Using Piezoceramic Smart Materials: A Review. Eng. Struct. 2006, 28, 1513–1524. [Google Scholar] [CrossRef]
- Bandyopadhyay, B.; Manjunath, T.C.; Umapathy, M. Modeling, Control and Implementation of Smart Structures A FEM-State Space Approach; Springer: Berlin/Heidelberg, Germany, 2007; ISBN 978-3-540-48393-9. [Google Scholar]
- Miara, B.; Stavroulakis, G.; Valente, V. Topics on Mathematics for Smart Systems. In Proceedings of the European Conference, Rome, Italy, 26–28 October 2006. [Google Scholar]
- Moutsopoulou, A.; Stavroulakis, G.E.; Pouliezos, A.; Petousis, M.; Vidakis, N. Robust Control and Active Vibration Suppression in Dynamics of Smart Systems. Inventions 2023, 8, 47. [Google Scholar] [CrossRef]
- Zhang, N.; Kirpitchenko, I. Modelling Dynamics of a Continuous Structure with a Piezoelectric Sensoractuator for Passive Structural Control. J. Sound Vib. 2002, 249, 251–261. [Google Scholar] [CrossRef]
- Stavropoulos, P.; Manitaras, D.; Papaioannou, C.; Souflas, T.; Bikas, H. Development of a Sensor Integrated Machining Vice towards a Non-Invasive Milling Monitoring System BT —Flexible Automation and Intelligent Manufacturing: The Human-Data-Technology Nexus; Kim, K.-Y., Monplaisir, L., Rickli, J., Eds.; Springer International Publishing: Cham, Switzerland, 2023; p. 29. [Google Scholar]
- Stavropoulos, P. Digitization of Manufacturing Processes: From Sensing to Twining. Technologies 2022, 10, 98. [Google Scholar] [CrossRef]
- Vidakis, N.; Petousis, M.; Moutsopoulou, A.; Mountakis, N.; Grammatikos, S.; Papadakis, V.; Tsikritzis, D. Biomedical Engineering Advances Cost-Effective Bi-Functional Resin Reinforced with a Nano-Inclusion Blend for Vat Photopolymerization Additive Manufacturing: The Effect of Multiple Antibacterial Nanoparticle Agents. Biomed. Eng. Adv. 2023, 5, 100091. [Google Scholar] [CrossRef]
- Stavropoulos, P.; Souflas, T.; Papaioannou, C.; Bikas, H.; Mourtzis, D. An Adaptive, Artificial Intelligence-Based Chatter Detection Method for Milling Operations. Int. J. Adv. Manuf. Technol. 2023, 124, 2037–2058. [Google Scholar] [CrossRef]
- Ward, R.; Sun, C.; Dominguez-Caballero, J.; Ojo, S.; Ayvar-Soberanis, S.; Curtis, D.; Ozturk, E. Machining Digital Twin Using Real-Time Model-Based Simulations and Lookahead Function for Closed Loop Machining Control. Int. J. Adv. Manuf. Technol. 2021, 117, 3615–3629. [Google Scholar] [CrossRef]
- Afazov, S.; Scrimieri, D. Chatter Model for Enabling a Digital Twin in Machining. Int. J. Adv. Manuf. Technol. 2020, 110, 2439–2444. [Google Scholar] [CrossRef]
- Zhang, X.; Shao, C.; Li, S.; Xu, D.; Erdman, A.G. Robust H∞ Vibration Control for Flexible Linkage Mechanism Systems with Piezoelectric Sensors and Actuators. J. Sound Vib. 2001, 243, 145–155. [Google Scholar] [CrossRef]
- Packard, A.; Doyle, J.; Balas, G. Linear, Multivariable Robust Control with a μ Perspective. J. Dyn. Syst. Meas. Control 1993, 115, 426–438. [Google Scholar] [CrossRef]
- Stavroulakis, G.E.; Foutsitzi, G.; Hadjigeorgiou, E.; Marinova, D.; Baniotopoulos, C.C. Design and Robust Optimal Control of Smart Beams with Application on Vibrations Suppression. Adv. Eng. Softw. 2005, 36, 806–813. [Google Scholar] [CrossRef]
- Kimura, H. Robust Stabilizability for a Class of Transfer Functions. IEEE Trans. Automat. Control 1984, 29, 788–793. [Google Scholar] [CrossRef]
- Burke, J.V.; Henrion, D.; Lewis, A.S.; Overton, M.L. Stabilization via Nonsmooth, Nonconvex Optimization. IEEE Trans. Automat. Control 2006, 51, 1760–1769. [Google Scholar] [CrossRef]
- Karpenko, M.; Stosiak, M.; Deptuła, A.; Urbanowicz, K.; Nugaras, J.; Królczyk, G.; Żak, K. Performance Evaluation of Extruded Polystyrene Foam for Aerospace Engineering Applications Using Frequency Analyses. Int. J. Adv. Manuf. Technol. 2023, 126, 5515–5526. [Google Scholar] [CrossRef]
- Karpenko, M.; Skačkauskas, P.; Prentkovskis, O. Methodology for the Composite Tire Numerical Simulation Based on the Frequency Response Analysis. Eksploat. Niezawodn.-Maint. Reliab. 2023, 25, 163289. [Google Scholar] [CrossRef]
- Doyle, J.; Glover, K.; Khargonekar, P.; Francis, B. State-Space Solutions to Standard H2 and H∞ Control Problems. In Proceedings of the 1988 American Control Conference, Atlanta, GA, USA, 15–17 June 1988; pp. 1691–1696. [Google Scholar]
- Francis, B.A. A Course in H∞ Control Theory; Springer: Berlin/Heidelberg, Germany, 1987; ISBN 978-3-540-17069-3. [Google Scholar]
- Friedman, Z.; Kosmatka, J.B. An Improved Two-Node Timoshenko Beam Finite Element. Comput. Struct. 1993, 47, 473–481. [Google Scholar] [CrossRef]
- Tiersten, H.F. Linear Piezoelectric Plate Vibrations: Elements of the Linear Theory of Piezoelectricity and the Vibrations Piezoelectric Plates, 1st ed.; Springer: New York, NY, USA, 1969; ISBN 978-1-4899-6221-8. [Google Scholar]
- Turchenko, V.A.; Trukhanov, S.V.; Kostishin, V.G.; Damay, F.; Porcher, F.; Klygach, D.S.; Vakhitov, M.G.; Lyakhov, D.; Michels, D.; Bozzo, B.; et al. Features of Structure, Magnetic State and Electrodynamic Performance of SrFe12−xInxO19. Sci. Rep. 2021, 11, 18342. [Google Scholar] [CrossRef]
- Kwakernaak, H. Robust Control and H∞-Optimization—Tutorial Paper. Automatica 1993, 29, 255–273. [Google Scholar] [CrossRef]
- Chandrashekhara, K.; Varadarajan, S. Adaptive Shape Control of Composite Beams with Piezoelectric Actuators. J. Intell. Mater. Syst. Struct. 1997, 8, 112–124. [Google Scholar] [CrossRef]
- Lim, Y.-H.; Gopinathan, S.V.; Varadan, V.V.; Varadan, V.K. Finite Element Simulation of Smart Structures Using an Optimal Output Feedback Controller for Vibration and Noise Control. Smart Mater. Struct. 1999, 8, 324–337. [Google Scholar] [CrossRef]
- Zames, G.; Francis, B. Feedback, Minimax Sensitivity, and Optimal Robustness. IEEE Trans. Automat. Control 1983, 28, 585–601. [Google Scholar] [CrossRef]
- Zhang, Q.M.; Pan, W.Y.; Jang, S.J.; Cross, L.E. Domain wall excitations and their contributions to the weak-signal response of doped lead zirconate titanate ceramics. J. Appl. Phys. 1988, 64, 6445–6451. [Google Scholar] [CrossRef]
- Hall, D.A. Nonlinearity in piezoelectric ceramics. J. Mater. Sci. 2001, 36, 4575–4601. [Google Scholar] [CrossRef]
- Kugel, D.; Cross, L.E. Behavior of soft piezoelectric ceramics under high sinusoidal electric fields. J. Appl. Phys. 1998, 84, 2815–2830. [Google Scholar] [CrossRef]
- Li, S.; Cao, W.; Cross, L.E. The extrinsic nature of nonlinear behavior observed in Lead Zirconate Titanate ferroelectric ceramic. J. Appl. Phys. 1991, 69, 7219–7224. [Google Scholar] [CrossRef]
- Garcia, J.E.; Pérez, R.; Ochoa, D.A.; Albareda, A.; Lente, M.H.; Eiras, J.A. Evaluation of domain wall motion in lead zirconate titanate ceramics by nonlinear response measurements. J. Appl. Phys. 2008, 103, 054108. [Google Scholar] [CrossRef]
- Stark, R.; Fresemann, C.; Lindow, K. Development and operation of Digital Twins for technical systems and services. CIRP Ann. 2019, 68, 129–132. [Google Scholar] [CrossRef]
- Czichos, H. Measurement, Testing and Sensor Technology: Fundamentals and Application to Materials and Technical Systems; Springer International Publishing: Cham, Switzerland, 2018; ISBN 978-3-319-76384-2. [Google Scholar]
- Vorwerk-Handing, G.; Gwosch, T.; Schork, S.; Kirchner, E.; Matthiesen, S. Classification and examples of next generation machine elements. Forsch. Ing. 2020, 84, 21–32. [Google Scholar] [CrossRef]
- Kirchner, E. Werkzeuge und Methoden der Produktentwicklung: Von der Idee Zum Erfolgreichen Produkt; Springer: Berlin/Heidelberg, Germany, 2020; ISBN 978-3-662-61762-5. [Google Scholar]
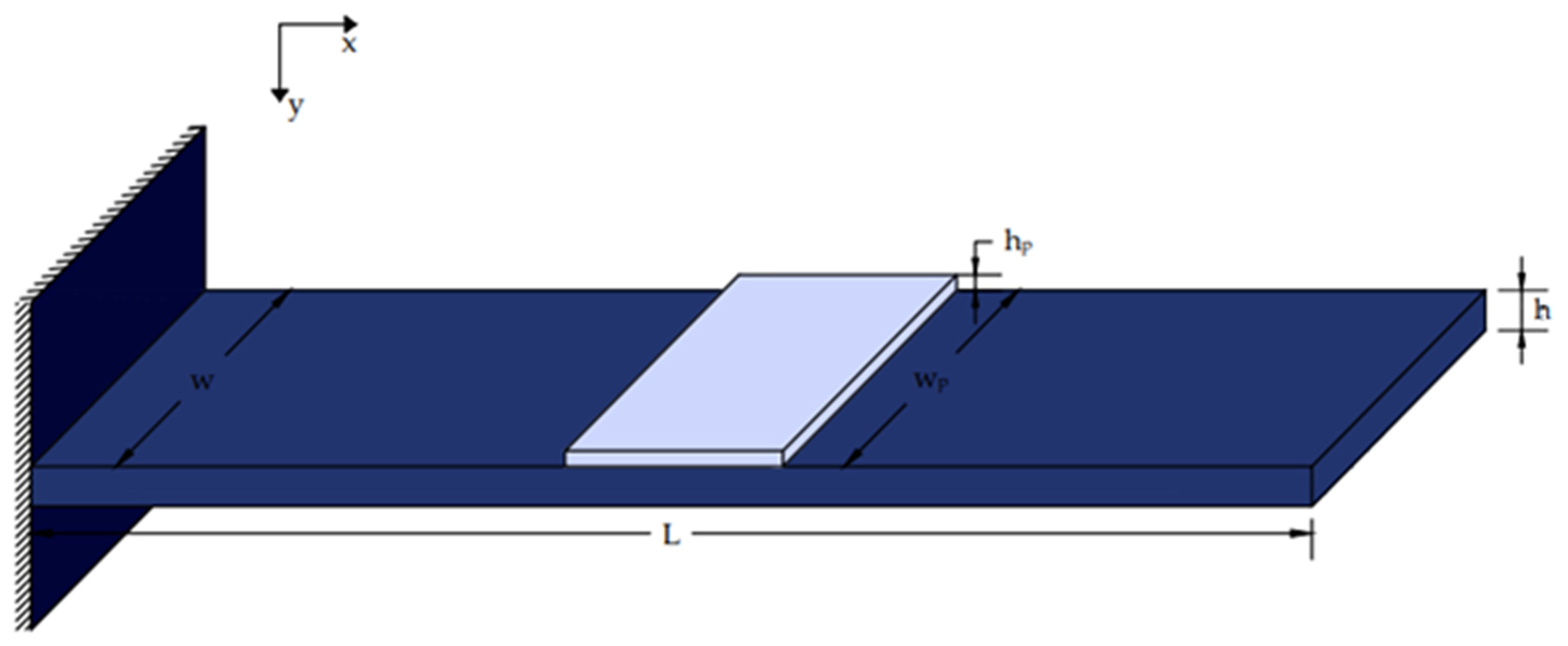











| Parameters | Values |
|---|---|
| L, for beam length | 1.20 m |
| W, for beam Width | 0.08 m |
| h, for beam thickness | 0.02 m |
| ρ, for beam density | 1700 kg/m3 |
| E, for Young’s modulus of the beam | 1.6 × 1011 N/m2 |
| bs, ba, for Pzt thickness | 0.002 m |
| d31 the Piezoelectric constant | 280 × 10−12 m/V |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moutsopoulou, A.; Petousis, M.; Vidakis, N.; Pouliezos, A.; Stavroulakis, G.E. Piezoelectric Actuators in Smart Engineering Structures Using Robust Control. Materials 2024, 17, 2357. https://doi.org/10.3390/ma17102357
Moutsopoulou A, Petousis M, Vidakis N, Pouliezos A, Stavroulakis GE. Piezoelectric Actuators in Smart Engineering Structures Using Robust Control. Materials. 2024; 17(10):2357. https://doi.org/10.3390/ma17102357
Chicago/Turabian StyleMoutsopoulou, Amalia, Markos Petousis, Nectarios Vidakis, Anastasios Pouliezos, and Georgios E. Stavroulakis. 2024. "Piezoelectric Actuators in Smart Engineering Structures Using Robust Control" Materials 17, no. 10: 2357. https://doi.org/10.3390/ma17102357







