Using Machine Learning to Evaluate the Value of Genetic Liabilities in the Classification of Hypertension within the UK Biobank
Abstract
:1. Introduction
2. Material and Method
2.1. Ethical Approval
2.2. Study Population
2.3. Genotyping and Imputation
2.4. Definition of the Outcome
2.5. Demographics and Clinical and Lifestyle Features
2.6. Computation of Genetic Liabilities
SNP Selection
2.7. Statistical Analysis
2.8. Data Preprocessing and Splitting
2.9. Handling Data Imbalance
2.10. Machine Learning Model Construction
2.10.1. Stage One Models
2.10.2. Stage Two Models
2.11. Model Performance Assessment Using Calibration
2.12. Net Reclassification Index and Integrated Discrimination Index
- https://github.com/GMaccarthy/NN_with_Imbalanced_Trainingset, accessed on 30 April 2024;
- https://github.com/GMaccarthy/NN_with_Balanced_Trainingset, accessed on 30 April 2024;
- https://github.com/GMaccarthy/RF_Balanced_trainingset, accessed on 30 April 2024;
- https://github.com/GMaccarthy/RF_Imbalaced_Trainingset, accessed on 30 April 2024.
3. Results
3.1. Baseline Characteristics of the Participants
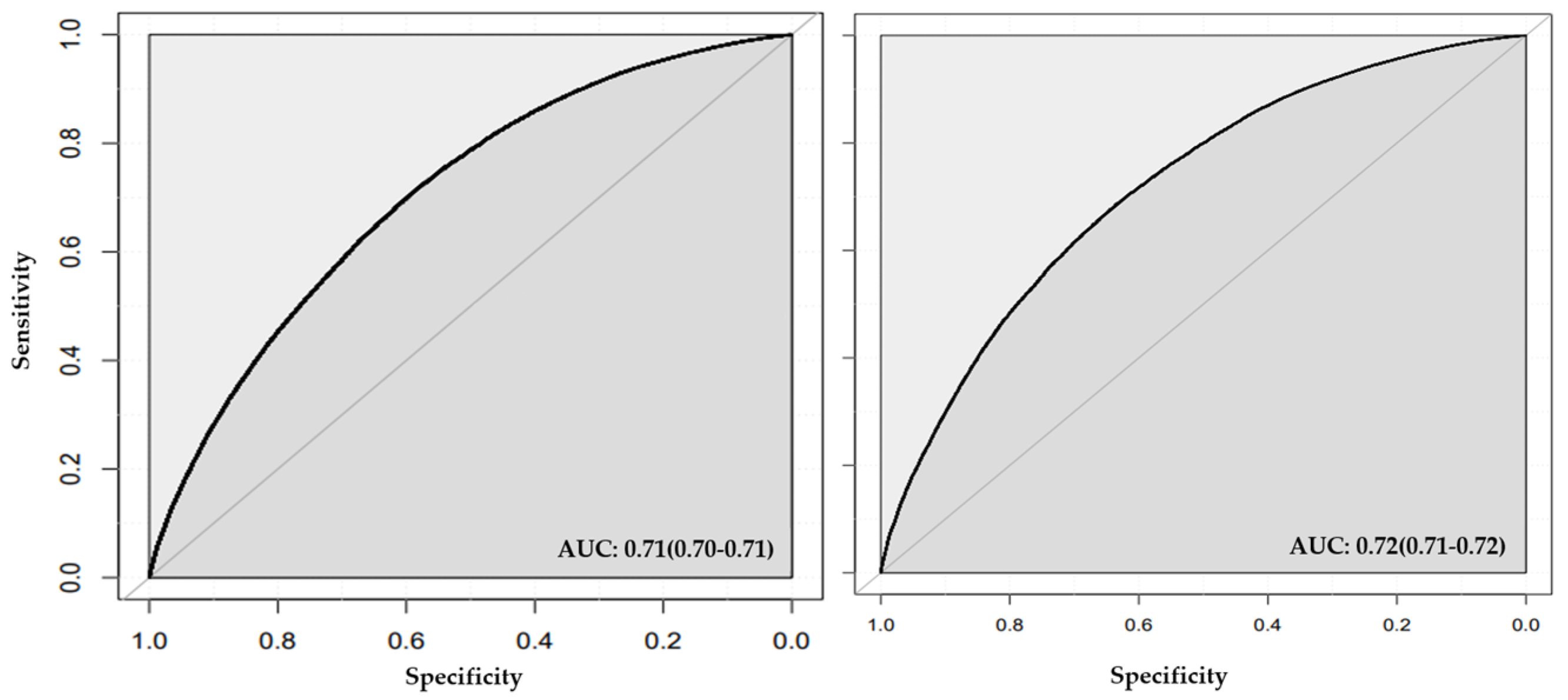
3.2. Stage One Models
3.3. Stage Two Models
3.4. Reclassification Index Analysis
4. Discussion
4.1. Strength
4.2. Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Available online: https://www.who.int/news-room/fact-sheets/detail/hypertension (accessed on 21 November 2023).
- Mills, K.T.; Stefanescu, A.; He, J. The global epidemiology of hypertension. Nat. Rev. Nephrol. 2020, 16, 223–237. [Google Scholar] [CrossRef] [PubMed]
- Roth, G.A.; Johnson, C.; Abajobir, A.; Abd-Allah, F.; Abera, S.F.; Abyu, G.; Ahmed, M.; Aksut, B.; Alam, T.; Alam, K.; et al. Global, Regional, and National Burden of Cardiovascular Diseases for 10 Causes, 1990 to 2015. J. Am. Coll. Cardiol. 2017, 70, 1–25. [Google Scholar] [CrossRef] [PubMed]
- Abdulkader, R.S.; Abera, S.F.; Acharya, D.; Aichour, I.; Aichour, M.T.E.; Akseer, N.; Al-Mekhlafi, H.M.; Aljunid, S.M.; Altirkawi, K.; Ayer, R.; et al. Global, regional, and national comparative risk assessment of 84 behavioural, environmental and occupational, and metabolic risks or clusters of risks for 195 countries and territories, 1990–2017: A systematic analysis for the Global Burden of Disease Study 2017. Lancet 2018, 392, 1923–1994. [Google Scholar]
- Available online: https://cks.nice.org.uk/topics/hypertension/background-information/prevalence/ (accessed on 22 November 2023).
- Available online: https://www.gov.uk/government/publications/health-matters-combating-high-blood-pressure/health-matters-combating-high-blood-pressure (accessed on 22 November 2023).
- Whelton, P.K.; Carey, R.M.; Aronow, W.S.; Casey, J.; Donald, E.; Collins, K.J.; Dennison Himmelfarb, C.; DePalma, S.M.; Gidding, S.; Jamerson, K.A.; et al. 2017 ACC/AHA/AAPA/ABC/ACPM/AGS/APhA/ASH/ASPC/NMA/PCNA Guideline for the Prevention, Detection, Evaluation, and Management of High Blood Pressure in Adults: A Report of the American College of Cardiology/American Heart Association Task Force on Clinical Practice Guidelines. J. Am. Coll. Cardiol. 2018, 71, e127–e248. [Google Scholar] [PubMed]
- Schneider, R.; Salerno, J.; Brook, R. 2020 International Society of Hypertension global hypertension practice guidelines—Lifestyle modification. J. Hypertens. 2020, 38, 2340–2341. [Google Scholar] [CrossRef] [PubMed]
- Williams, B.; Mancia, G.; Spiering, W.; Agabiti Rosei, E.; Azizi, M.; Burnier, M.; Clement, D.L.; Coca, A.; de Simone, G.; Dominiczak, A.; et al. 2018 ESC/ESH Guidelines for the management of arterial hypertension. J. Hypertens. 2018, 36, 1953–2041. [Google Scholar] [CrossRef] [PubMed]
- Nicoll, R.; Henein, M.Y. Hypertension and lifestyle modification: How useful are the guidelines? Br. J. Gen. Pract. 2010, 60, 879–880. [Google Scholar] [CrossRef] [PubMed]
- Natarajan, P. Polygenic Risk Scoring for Coronary Heart Disease: The First Risk Factor. J. Am. Coll. Cardiol. 2018, 72, 1894–1897. [Google Scholar] [CrossRef] [PubMed]
- Ehret, G.B. Genome-Wide Association Studies: Contribution of Genomics to Understanding Blood Pressure and Essential Hypertension. Curr. Hypertens. Rep. 2010, 12, 17–25. [Google Scholar] [CrossRef]
- Hwang, S.; Vasan, R.S.; O’Donnell, C.J.; Levy, D.; Mattace-Raso, F.U.S.; Morrison, A.C.; Scharpf, R.B.; Psaty, B.M.; Rice, K.; Harris, T.B.; et al. Genome-wide association study of blood pressure and hypertension. Nat. Genet. 2009, 41, 677–687. [Google Scholar]
- Munroe, P.B.; Smith, A.V.; Verwoert, G.C.; Amin, N.; Teumer, A.; Zhao, J.H.; Parsa, A.; Dehghan, A.; Peden, J.F.; Rudan, I.; et al. Genetic variants in novel pathways influence blood pressure and cardiovascular disease risk. Nature 2011, 478, 103–109. [Google Scholar]
- Ferreira, T.; Chasman, D.I.; Johnson, T.; Luan, J.; Donnelly, L.A.; Kanoni, S.; Strawbridge, R.J.; Meirelles, O.; Bouatia-Naji, N.; Salfati, E.L.; et al. The genetics of blood pressure regulation and its target organs from association studies in 342,415 individuals. Nat. Genet. 2016, 48, 1171–1184. [Google Scholar]
- Hoffmann, T.J.; Ehret, G.B.; Nandakumar, P.; Ranatunga, D.; Schaefer, C.; Kwok, P.; Iribarren, C.; Chakravarti, A.; Risch, N. Genome-wide association analyses using electronic health records identify new loci influencing blood pressure variation. Nat. Genet. 2017, 49, 54–64. [Google Scholar] [CrossRef] [PubMed]
- Warren, H.R.; Evangelou, E.; Cabrera, C.P.; Gao, H.; Ren, M.; Mifsud, B.; Ntalla, I.; Surendran, P.; Liu, C.; Cook, J.P.; et al. Genome-wide association analysis identifies novel blood pressure loci and offers biological insights into cardiovascular risk. Nat. Genet. 2017, 49, 403–415. [Google Scholar] [CrossRef] [PubMed]
- Wang, A.; An, N.; Chen, G.; Li, L.; Alterovitz, G. Predicting hypertension without measurement: A non-invasive, questionnaire-based approach. Expert Syst. Appl. 2015, 42, 7601–7609. [Google Scholar] [CrossRef]
- Kanegae, H.; Oikawa, T.; Suzuki, K.; Okawara, Y.; Kario, K. Developing and validating a new precise risk-prediction model for new-onset hypertension: The Jichi Genki hypertension prediction model (JG model). J. Clin. Hypertens. 2018, 20, 880–890. [Google Scholar] [CrossRef] [PubMed]
- Kanegae, H.; Suzuki, K.; Fukatani, K.; Ito, T.; Harada, N.; Kario, K. Highly precise risk prediction model for new-onset hypertension using artificial intelligence techniques. J. Clin. Hypertens. 2020, 22, 445–450. [Google Scholar] [CrossRef] [PubMed]
- AlKaabi, L.A.; Ahmed, L.S.; Al Attiyah, M.F.; Abdel-Rahman, M.E. Predicting hypertension using machine learning: Findings from Qatar Biobank Study. PLoS ONE 2020, 15, e0240370. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Zhang, X.; Xu, Y.; Gao, L.; Ma, Z.; Sun, Y.; Wang, W. Predicting the Risk of Hypertension Based on Several Easy-to-Collect Risk Factors: A Machine Learning Method. Front. Public Health 2021, 9, 619429. [Google Scholar] [CrossRef]
- Pengo, M.; Montagna, S.; Ferretti, S.; Bilo, G.; Borghi, C.; Ferri, C.; Grassi, G.; Muiesan, M.L.; Parati, G. Machine learning in hypertension detection: A study on world hypertension day data. J. Hypertens. 2023, 41 (Suppl. S3), e94. [Google Scholar] [CrossRef]
- Fava, C.; Sjögren, M.; Olsson, S.; Lövkvist, H.; Jood, K.; Engström, G.; Hedblad, B.; Norrving, B.; Jern, C.; Lindgren, A.; et al. A genetic risk score for hypertension associates with the risk of ischemic stroke in a Swedish case–control study. Eur. J. Hum. Genet. 2015, 23, 969–974. [Google Scholar] [CrossRef] [PubMed]
- Niu, M.; Wang, Y.; Zhang, L.; Tu, R.; Liu, X.; Hou, J.; Huo, W.; Mao, Z.; Wang, C.; Bie, R. Identifying the predictive effectiveness of a genetic risk score for incident hypertension using machine learning methods among populations in rural China. Hypertens. Res. 2021, 44, 1483–1491. [Google Scholar] [CrossRef]
- Huang, H.; Xu, T.; Yang, J. Comparing logistic regression, support vector machines, and permanental classification methods in predicting hypertension. BMC Proc. 2014, 8 (Suppl. S1), S96. [Google Scholar] [CrossRef]
- Held, E.; Cape, J.; Tintle, N. Comparing machine learning and logistic regression methods for predicting hypertension using a combination of gene expression and next-generation sequencing data. BMC Proc. 2016, 10 (Suppl. S7), 141–145. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Huang, J.; Wang, L.; Chen, S.; Yang, X.; Li, J.; Cao, J.; Chen, J.; Li, Y.; Zhao, L.; et al. Genetic Predisposition to Higher Blood Pressure Increases Risk of Incident Hypertension and Cardiovascular Diseases in Chinese. Hypertension 2015, 66, 786–792. [Google Scholar] [CrossRef] [PubMed]
- Vaura, F.; Kauko, A.; Suvila, K.; Havulinna, A.S.; Mars, N.; Salomaa, V.; Gen, F.; Cheng, S.; Niiranen, T. Polygenic Risk Scores Predict Hypertension Onset and Cardiovascular Risk. Hypertension 2021, 77, 1119–1127. [Google Scholar] [CrossRef]
- Li, C.; Sun, D.; Liu, J.; Li, M.; Zhang, B.; Liu, Y.; Wang, Z.; Wen, S.; Zhou, J. A Prediction Model of Essential Hypertension Based on Genetic and Environmental Risk Factors in Northern Han Chinese. Int. J. Med. Sci. 2019, 16, 793–799. [Google Scholar] [CrossRef]
- Albiñana, C.; Zhu, Z.; Schork, A.; Ingason, A.; Aschard, H.; Brikell, I.; Bulik, C.; Petersen, L.; Agerbo, E.; Grove, J.; et al. Multi-PGS enhances polygenic prediction: Weighting 937 polygenic scores. Nat. Commun. 2023, 14, 4702. [Google Scholar] [CrossRef]
- Abraham, G.; Malik, R.; Yonova-Doing, E.; Salim, A.; Wang, T.; Danesh, J.; Butterworth, A.S.; Howson, J.M.M.; Inouye, M.; Dichgans, M. Genomic risk score offers predictive performance comparable to clinical risk factors for ischaemic stroke. Nat. Commun. 2019, 10, 5819. [Google Scholar] [CrossRef]
- Krapohl, E.; Patel, H.; Newhouse, S.; Curtis, C.J.; von Stumm, S.; Dale, P.S.; Zabaneh, D.; Breen, G.; O’Reilly, P.F.; Plomin, R. Multi-polygenic score approach to trait prediction. Mol. Psychiatry 2018, 23, 1368–1374. [Google Scholar] [CrossRef]
- Sun, D.; Zhou, T.; Heianza, Y.; Li, X.; Fan, M.; Fonseca, V.; Qi, L. Type 2 Diabetes and Hypertension: A Study on Bidirectional Causality. Circ. Res. 2019, 124, 930–937. [Google Scholar] [CrossRef]
- Giontella, A.; Lotta, L.A.; Overton, J.D.; Baras, A.; Minuz, P.; Melander, O.; Gill, D.; Fava, C. Causal Effect of Adiposity Measures on Blood Pressure Traits in 2 Urban Swedish Cohorts: A Mendelian Randomization Study. J. Am. Heart Assoc. 2021, 10, e020405. [Google Scholar] [CrossRef] [PubMed]
- Miao, K.; Wang, Y.; Cao, W.; Lv, J.; Yu, C.; Huang, T.; Sun, D.; Liao, C.; Pang, Y.; Hu, R.; et al. Genetic and Environmental Influences on Blood Pressure and Serum Lipids Across Age-Groups. Twin Res. Hum. Genet. 2023, 26, 223–230. [Google Scholar] [CrossRef]
- Cadby, G.; Melton, P.E.; McCarthy, N.S.; Giles, C.; Mellett, N.A.; Huynh, K.; Hung, J.; Beilby, J.; Dubé, M.; Watts, G.F.; et al. Heritability of 596 lipid species and genetic correlation with cardiovascular traits in the Busselton Family Heart Study[S]. J. Lipid Res. 2020, 61, 537–545. [Google Scholar] [CrossRef] [PubMed]
- Larsson, S.C.; Mason, A.M.; Bäck, M.; Klarin, D.; Damrauer, S.M.; Million Veteran Program; Michaëlsson, K.; Burgess, S. Genetic predisposition to smoking in relation to 14 cardiovascular diseases. Eur. Heart J. 2020, 41, 3304–3310. [Google Scholar] [CrossRef]
- Sudlow, C.; Gallacher, J.; Allen, N.; Beral, V.; Burton, P.; Danesh, J.; Downey, P.; Elliott, P.; Green, J.; Landray, M.; et al. UK Biobank: An Open Access Resource for Identifying the Causes of a Wide Range of Complex Diseases of Middle and Old Age. PLoS Med. 2015, 12, e1001779. [Google Scholar] [CrossRef] [PubMed]
- Bycroft, C.; Freeman, C.; Petkova, D.; Band, G.; Elliott, L.; Sharp, K.; Motyer, A.; Vukcevic, D.; Delaneau, O.; O’connell, J.; et al. Genome-wide genetic data on ~500,000 UK biobank participants. bioRxiv 2017. [Google Scholar] [CrossRef]
- Welsh, S.; Peakman, T.; Sheard, S.; Almond, R. Comparison of DNA quantification methodology used in the DNA extraction protocol for the UK Biobank cohort. BMC Genom. 2017, 18, 26. [Google Scholar] [CrossRef]
- Bycroft, C.; Freeman, C.; Petkova, D.; Band, G.; Elliott, L.T.; Sharp, K.; Motyer, A.; Vukcevic, D.; Delaneau, O.; O’Connell, J.; et al. The Uk biobank resource with deep phenotyping and genomic data. Nature 2018, 562, 203–209. [Google Scholar] [CrossRef]
- Flack, J.M.; Adekola, B. Blood pressure and the new ACC/AHA hypertension guidelines. Trends Cardiovasc. Med. 2020, 30, 160–164. [Google Scholar] [CrossRef]
- Pazoki, R.; Dehghan, A.; Evangelou, E.; Warren, H.; Gao, H.; Caulfield, M.; Elliott, P.; Tzoulaki, I. Genetic Predisposition to High Blood Pressure and Lifestyle Factors: Associations with Midlife Blood Pressure Levels and Cardiovascular Events. Circulation 2018, 137, 653–661. [Google Scholar] [CrossRef] [PubMed]
- Sacks, D.B.; Arnold, M.; Bakris, G.L.; Bruns, D.E.; Horvath, A.R.; Kirkman, M.S.; Lernmark, A.; Metzger, B.E.; Nathan, D.M. Guidelines and Recommendations for Laboratory Analysis in the Diagnosis and Management of Diabetes Mellitus. Clin. Chem. 2011, 57, e1–e47. [Google Scholar] [CrossRef] [PubMed]
- Mahajan, A.; Taliun, D.; Thurner, M.; Robertson, N.R.; Torres, J.M.; Payne, A.J.; Steinthorsdottir, V.; Scott, R.A.; Grarup, N.; Wuttke, M.; et al. Fine-mapping type 2 diabetes loci to single-variant resolution using high-density imputation and islet-specific epigenome maps. Nat. Genet. 2018, 50, 1505–1513. [Google Scholar] [CrossRef] [PubMed]
- Winkler, T.W.; Justice, A.E.; Rueeger, S.; Teumer, A.; Ehret, G.B.; Heard-Costa, N.L.; Jansen, R.; Craen, A.J.M.; Boucher, G.; Cheng, Y.; et al. The Influence of Age and Sex on Genetic Associations with Adult Body Size and Shape: A Large-Scale Genome-Wide Interaction Study. PLoS Genet. 2016, 12, e1006166. [Google Scholar] [CrossRef] [PubMed]
- Shungin, D.; Winkler, T.W.; Croteau-Chonka, D.C.; Ferreira, T.; Locke, A.E.; Mägi, R.; Strawbridge, R.J.; Pers, T.H.; Fischer, K.; Justice, A.E.; et al. New genetic loci link adipose and insulin biology to body fat distribution. Nature 2015, 518, 187–196. [Google Scholar] [CrossRef]
- Liu, M.; Jiang, Y.; Wedow, R.; Brazel, D.M.; Zhan, X.; Agee, M.; Bryc, K.; Fontanillas, P.; Furlotte, N.A.; Hinds, D.A.; et al. Association studies of up to 1.2 million individuals yield new insights into the genetic etiology of tobacco and alcohol use. Nat. Genet. 2019, 51, 237–244. [Google Scholar] [CrossRef] [PubMed]
- Surakka, I.; Horikoshi, M.; Mägi, R.; Sarin, A.; Mahajan, A.; Lagou, V.; Marullo, L.; Ferreira, T.; Miraglio, B.; Timonen, S.; et al. The impact of low-frequency and rare variants on lipid levels. Nat. Genet. 2015, 47, 589–597. [Google Scholar] [CrossRef]
- Marees, A.T.; de Kluiver, H.; Stringer, S.; Vorspan, F.; Curis, E.; Marie-Claire, C.; Derks, E.M. A tutorial on conducting genome-wide association studies: Quality control and statistical analysis. Int. J. Methods Psychiatr. Res. 2018, 27, e1608. [Google Scholar] [CrossRef]
- Chang, C.C.; Chow, C.C.; Tellier, L.C.; Vattikuti, S.; Purcell, S.M.; Lee, J.J. Second-generation PLINK: Rising to the challenge of larger and richer datasets. GigaScience 2015, 4, 7. [Google Scholar] [CrossRef]
- Ozsahin, D.U.; Mustapha, M.T.; Mubarak, A.S.; Ameen, Z.S.; Uzun, B. Impact of feature scaling on machine learning models for the diagnosis of diabetes. In Proceedings of the 2022 International Conference on Artificial Intelligence in Everything (AIE), Lefkosa, Cyprus, 2–4 August 2022; The Institute of Electrical and Electronics Engineers, Inc. (IEEE): Piscataway, NJ, USA, 2022. [Google Scholar]
- Nguyen, Q.H.; Ly, H.; Ho, L.S.; Al-Ansari, N.; Le, H.V.; Tran, V.Q.; Prakash, I.; Pham, B.T. Influence of Data Splitting on Performance of Machine Learning Models in Prediction of Shear Strength of Soil. Math. Probl. Eng. 2021, 2021, 4832864. [Google Scholar] [CrossRef]
- Pencina, M.J.; D’Agostino, R.B. Evaluating Discrimination of Risk Prediction Models: The C Statistic. JAMA 2015, 314, 1063–1064. [Google Scholar] [CrossRef] [PubMed]
- Xin, J.; Chu, H.; Ben, S.; Ge, Y.; Shao, W.; Zhao, Y.; Wei, Y.; Ma, G.; Li, S.; Gu, D.; et al. Evaluating the effect of multiple genetic risk score models on colorectal cancer risk prediction. Gene 2018, 673, 174–180. [Google Scholar] [CrossRef] [PubMed]
- Nartowt, B.J.; Hart, G.R.; Roffman, D.A.; Llor, X.; Ali, I.; Muhammad, W.; Liang, Y.; Deng, J. Scoring colorectal cancer risk with an artificial neural network based on self-reportable personal health data. PLoS ONE 2019, 14, e0221421. [Google Scholar] [CrossRef] [PubMed]
- Kavalci, E.; Hartshorn, A. Improving clinical trial design using interpretable machine learning based prediction of early trial termination. Sci. Rep. 2023, 13, 121. [Google Scholar] [CrossRef] [PubMed]
- Wei, Q.; Dunbrack, J.; Roland, L. The Role of Balanced Training and Testing Data Sets for Binary Classifiers in Bioinformatics. PLoS ONE 2013, 8, e67863. [Google Scholar] [CrossRef]
- Johnson, J.M.; Khoshgoftaar, T.M. Survey on deep learning with class imbalance. J. Big Data 2019, 6, 27. [Google Scholar] [CrossRef]
- Lunardon, N.; Menardi, G.; Torelli, N. ROSE: A Package for Binary Imbalanced Learning. R J. 2014, 6, 79. [Google Scholar] [CrossRef]
- Kufel, J.; Bargieł-Łączek, K.; Kocot, S.; Koźlik, M.; Bartnikowska, W.; Janik, M.; Czogalik, Ł.; Dudek, P.; Magiera, M.; Lis, A.; et al. What Is Machine Learning, Artificial Neural Networks and Deep Learning?—Examples of Practical Applications in Medicine. Diagnostics 2023, 13, 2582. [Google Scholar] [CrossRef]
- Rajula, H.S.R.; Verlato, G.; Manchia, M.; Antonucci, N.; Fanos, V. Comparison of Conventional Statistical Methods with Machine Learning in Medicine: Diagnosis, Drug Development, and Treatment. Medicina 2020, 56, 455. [Google Scholar] [CrossRef]
- Montagna, S.; Pengo, M.; Ferretti, S.; Borghi, C.; Ferri, C.; Grassi, G.; Muiesan, M.; Parati, G. Machine Learning in Hypertension Detection: A Study on World Hypertension Day Data. J. Med. Syst. 2023, 47, 1. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Wright, M.N.; Ziegler, A. ranger: A fast implementation of random forests for high dimensional data in C++ and R. J. Stat. Softw. 2017, 77, 1–17. [Google Scholar] [CrossRef]
- Purkait, N. Hands-On Neural Networks with Keras: Birmingham; Packt Publishing: Birmingham, UK, 2019. [Google Scholar]
- Islam, M.M.; Alam, M.J.; Maniruzzaman, M.; Ahmed, N.A.M.F.; Ali, M.S.; Rahman, M.J.; Roy, D.C. Predicting the risk of hypertension using machine learning algorithms: A cross sectional study in Ethiopia. PLoS ONE 2023, 18, e0289613. [Google Scholar] [CrossRef] [PubMed]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S, 4th ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Ying, X. An Overview of Overfitting and its Solutions. J. Phys. Conf. Ser. 2019, 1168, 22022. [Google Scholar] [CrossRef]
- Arlot, S.; Celisse, A. A survey of cross-validation procedures for model selection. Stat. Surv. 2010, 4, 40–79. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning, 2nd ed.; Springer: New York, NY, USA, 2011. [Google Scholar]
- Hajian-Tilaki, K. Receiver Operating Characteristic (ROC) Curve Analysis for Medical Diagnostic Test Evaluation. Casp. J. Intern. Med. 2013, 4, 627–635. [Google Scholar]
- Lindhiem, O.; Petersen, I.T.; Mentch, L.K.; Youngstrom, E.A. The Importance of Calibration in Clinical Psychology. Assessment 2020, 27, 840–854. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Li, W.; Macheret, F.; Gabriel, R.A.; Ohno-Machado, L. A tutorial on calibration measurements and calibration models for clinical prediction models. J. Am. Med. Inform. Assoc. 2020, 27, 621–633. [Google Scholar] [CrossRef] [PubMed]
- Steyerberg, E.; Vickers, A.; Cook, N.; Gerds, T.; Gonen, M.; Obuchowski, N.; Pencina, M.; Kattan, M. Assessing the performance of prediction models: A framework for traditional and novel measures. Epidemiology 2010, 21, 128–138. [Google Scholar] [CrossRef]
- Steyerberg, E.W. Clinical Prediction Models: A Practical Approach to Development, Validation, and Updating, 2nd ed.; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Rufibach, K. Use of Brier score to assess binary predictions. J. Clin. Epidemiol. 2010, 63, 938–939. [Google Scholar] [CrossRef]
- McKearnan, S.B.; Wolfson, J.; Vock, D.M.; Vazquez-Benitez, G.; O’Connor, P.J. Performance of the Net Reclassification Improvement for Nonnested Models and a Novel Percentile-Based Alternative. Am. J. Epidemiol. 2018, 187, 1327–1335. [Google Scholar] [CrossRef] [PubMed]
- Kerr, K.F.; McClelland, R.L.; Brown, E.R.; Lumley, T. Evaluating the Incremental Value of New Biomarkers with Integrated Discrimination Improvement. Am. J. Epidemiol. 2011, 174, 364–374. [Google Scholar] [CrossRef] [PubMed]
- Martens, F.K.; Tonk, E.C.M.; Janssens, A.C.J.W. Evaluation of polygenic risk models using multiple performance measures: A critical assessment of discordant results. Genet. Med. 2019, 21, 391–397. [Google Scholar] [CrossRef] [PubMed]
- Borghi, C.; Veronesi, M.; Bacchelli, S.; Esposti, D.; Cosentino, E.; Ambrosioni, E. Serum cholesterol levels, blood pressure response to stress and incidence of stable hypertension in young subjects with high normal blood pressure. J. Hypertens. 2004, 22, 265–272. [Google Scholar] [CrossRef] [PubMed]
- Wildman, R.P.; Sutton-Tyrrell, K.; Newman, A.B.; Bostom, A.; Brockwell, S.; Kuller, L.H. Lipoprotein Levels Are Associated with Incident Hypertension in Older Adults. J. Am. Geriatr. Soc. 2004, 52, 916–921. [Google Scholar] [CrossRef] [PubMed]
- Ebrahimi, H.; Emamian, M.H.; Hashemi, H.; Fotouhi, A. Dyslipidemia and its risk factors among urban middle-aged Iranians: A population-based study. Diabetes Metab. Syndr. Clin. Res. Rev. 2016, 10, 149–156. [Google Scholar] [CrossRef] [PubMed]
- Xi, Y.; Niu, L.; Cao, N.; Bao, H.; Xu, X.; Zhu, H.; Yan, T.; Zhang, N.; Qiao, L.; Han, K.; et al. Prevalence of dyslipidemia and associated risk factors among adults aged ≥35 years in northern China: A cross-sectional study. BMC Public Health 2020, 20, 1068. [Google Scholar] [CrossRef] [PubMed]
- Wilkinson, I.B.; Prasad, K.; Hall, I.R.; Thomas, A.; MacCallum, H.; Webb, D.J.; Frenneaux, M.P.; Cockcroft, J.R. Increased central pulse pressure and augmentation index in subjects with hypercholesterolemia. J. Am. Coll. Cardiol. 2002, 39, 1005–1011. [Google Scholar] [CrossRef]
- Li, Y.R.; Keating, B.J. Trans-ethnic genome-wide association studies: Advantages and challenges of mapping in diverse populations. Genome Med. 2014, 6, 91. [Google Scholar] [CrossRef]
- Balogun, W.O.; Salako, B.L. Co-occurrence of diabetes and hypertension: Pattern and factors associated with order of diagnosis among nigerians. Ann. Ib. Postgrad. Med. 2011, 9, 89–93. [Google Scholar]
- Han, L.; Li, X.; Wang, X.; Zhou, J.; Wang, Q.; Rong, X.; Wang, G.; Shao, X. Effect of Hypertension, Waist-to-Height Ratio, and Their Transitions on the Risk of Type 2 Diabetes Mellitus: Analysis from the China Health and Retirement Longitudinal Study. J. Diabetes Res. 2022, 2022, 7311950. [Google Scholar] [CrossRef]
- Petrie, J.R.; Guzik, T.J.; Touyz, R.M. Diabetes, hypertension, and cardiovascular disease: Clinical insights and vascular mechanisms. Can. J. Cardiol. 2018, 34, 575–584. [Google Scholar] [CrossRef]
- Klop, B.; Elte, J.W.F.; Cabezas, M.C. Dyslipidemia in Obesity: Mechanisms and Potential Targets. Nutrients 2013, 5, 1218–1240. [Google Scholar] [CrossRef] [PubMed]
- Tyrrell, J.; Wood, A.R.; Ames, R.M.; Yaghootkar, H.; Beaumont, R.N.; Jones, S.E.; Tuke, M.A.; Ruth, K.S.; Freathy, R.M.; Davey Smith, G.; et al. Gene–obesogenic environment interactions in the UK Biobank study. Int. J. Epidemiol. 2017, 46, 559–575. [Google Scholar] [CrossRef]
- Khera, A.V.; Emdin, C.A.; Drake, I.; Natarajan, P.; Bick, A.G.; Cook, N.R.; Chasman, D.I.; Baber, U.; Mehran, R.; Rader, D.J.; et al. Genetic Risk, Adherence to a Healthy Lifestyle, and Coronary Disease. N. Engl. J. Med. 2016, 375, 2349–2358. [Google Scholar] [CrossRef]
- Hezekiah, C.; Blakemore, A.; Bailey, D.; Pazoki, R. Physical activity reduces the effect of adiposity genetic liability on hypertension risk in the UK Biobank cohort. medRxiv 2023. [Google Scholar] [CrossRef]
- Biau, D.J.; Kernéis, S.; Porcher, R. Statistics in Brief: The Importance of Sample Size in the Planning and Interpretation of Medical Research. Clin. Orthop. Relat. Res. 2008, 466, 2282–2288. [Google Scholar] [CrossRef] [PubMed]
- Andrade, C. Sample Size and its Importance in Research. Indian J. Psychol. Med. 2020, 42, 102–103. [Google Scholar] [CrossRef] [PubMed]
- Khera, A.V.; Chaffin, M.; Aragam, K.G.; Haas, M.E.; Roselli, C.; Choi, S.H.; Natarajan, P.; Lander, E.S.; Lubitz, S.A.; Ellinor, P.T.; et al. Genome-wide polygenic scores for common diseases identify individuals with risk equivalent to monogenic mutations. Nat. Genet. 2018, 50, 1219–1224. [Google Scholar] [CrossRef]
- Khera, A.V.; Chaffin, M.; Wade, K.H.; Zahid, S.; Brancale, J.; Xia, R.; Distefano, M.; Senol-Cosar, O.; Haas, M.E.; Bick, A.; et al. Polygenic Prediction of Weight and Obesity Trajectories from Birth to Adulthood. Cell 2019, 177, 587–596.e9. [Google Scholar] [CrossRef]
- Yun, J.; Jung, S.; Shivakumar, M.; Xiao, B.; Khera, A.V.; Won, H.; Kim, D. Polygenic risk for type 2 diabetes, lifestyle, metabolic health, and cardiovascular disease: A prospective UK Biobank study. Cardiovasc. Diabetol. 2022, 21, 131. [Google Scholar] [CrossRef] [PubMed]
- Newaz, A.; Mohosheu, M.S.; Al Noman, M.A. Predicting complications of myocardial infarction within several hours of hospitalization using data mining techniques. Inform. Med. Unlocked 2023, 42, 101361. [Google Scholar] [CrossRef]
- Thölke, P.; Mantilla-Ramos, Y.; Abdelhedi, H.; Maschke, C.; Dehgan, A.; Harel, Y.; Kemtur, A.; Mekki Berrada, L.; Sahraoui, M.; Young, T.; et al. Class imbalance should not throw you off balance: Choosing the right classifiers and performance metrics for brain decoding with imbalanced data. NeuroImage 2023, 277, 120253. [Google Scholar] [CrossRef] [PubMed]
- Lever, J.; Krzywinski, M.; Altman, N. Model selection and overfitting. Nat. Methods 2016, 13, 703–704. [Google Scholar] [CrossRef]





| Trait Category | Genetic Liability | Study (Publication Year) | Number of SNPs | Reference |
|---|---|---|---|---|
| Smoking | Smoking initiation | Liu et al., 2019 [49] | 311 | Liu et al., 2019 [49] |
| Smoking cessation | Liu et al., 2019 [49] | 16 | Liu et al., 2019 [49] | |
| Smoking heaviness | Liu et al., 2019 [49] | 38 | Liu et al., 2019 [49] | |
| Diabetes | Type 2 diabetes | Mahajan et al., 2018 [46] | 210 | Mahajan et al., 2018 [46] |
| Adiposity | BMI | Winkler et al., 2016 [47] | 159 | Winkler et al., 2016 [47] |
| WHR | Shungin et al., 2015 [48] | 39 | Shungin et al., 2015 [48] | |
| Lipid traits | TC | Surakka et al., 2015 [50] | 36 | Surakka et al., 2015 [50] |
| HDL | Surakka et al., 2015 [50] | 19 | Surakka et al., 2015 [50] | |
| LDL | Surakka et al., 2015 [50] | 30 | Surakka et al., 2015 [50] | |
| Triglycerides | Surakka et al., 2015 [50] | 25 | Surakka et al., 2015 [50] |
| Feature Category | Feature Type | Feature |
|---|---|---|
| Characteristics features |
| |
| Lifestyle-related features | Phenotype |
|
| Genetic |
| |
| Diabetes-related features | Phenotype |
|
| Genetic |
| |
| Adiposity-related features | Phenotype |
|
| Genetic |
| |
| Lipid-related features | Phenotype |
|
| Genetics |
|
| Hypertensive | Non-Hypertensive | Overall | p-Value | |
|---|---|---|---|---|
| N = 117,095 | N = 127,623 | N = 244,718 | ||
| Diabetes diagnosed by a doctor: | ||||
| YES; N (%) | 4697 (4.00%) | 2314 (1.80%) | 7011 (2.9%) | <0.001 |
| NO; N (%) | 112,398 (96.0%) | 125,309 (98.2%) | 237,707 (97.1%) | |
| Age (years); mean (SD) | 57.6 (7.53) | 53.4 (7.84) | 55.4 (7.98) | <0.001 |
| BMI (kg/m2); mean (SD) | 28.0 (4.83) | 25.8 (4.06) | 26.8 (4.58) | <0.001 |
| TC (mmol/L); mean (SD) | 6.05 (1.06) | 5.79 (1.04) | 5.91 (1.06) | <0.001 |
| HDL (mmol/L); mean (SD) | 1.46 (0.38) | 1.51 (0.38) | 1.49 (0.38) | <0.001 |
| LDL (mmol/L); mean (SD) | 3.84 (0.81) | 3.62 (0.80) | 3.73 (0.81) | <0.001 |
| Sedentary lifestyle (h/day); mean (SD) | 4.87 (2.39) | 4.50 (2.33) | 4.68 (2.37) | <0.001 |
| Sex: | ||||
| Male; N (%) | 55,686 (47.6%) | 47,101 (36.9%) | 10,2787 (42.0%) | <0.001 |
| Female; N (%) | 61,409 (52.4%) | 80,522 (63.1%) | 141,931 (58.0%) | |
| Drinking status: | ||||
| Current; N (%) | 109,655 (93.6%) | 119,884 (93.9%) | 229,539 (93.8%) | <0.001 |
| Never; N (%) | 4052 (3.46%) | 3967 (3.11%) | 8019 (3.3%) | |
| Previous; N (%) | 3388 (2.89%) | 3772 (2.96%) | 7160 (2.9%) | |
| Smoking status: | ||||
| Current; N (%) | 37,458 (32.0%) | 39,476 (30.9%) | 76,934 (31.4%) | <0.001 |
| Never; N (%) | 78,292 (66.9%) | 86,555 (67.8%) | 164,847 (67.4%) | |
| Previous; N (%) | 1345 (1.15%) | 1592 (1.25%) | 2937 (1.2%) |
| Classification Models | Numb of Features | R2 | AUC% (95% Cl) | Brier Score | Spiegel Halter z Score | Spiegel Halter p-Value | Slope | Intercept | Accuracy % (95% Cl) | Sensitivity (Recall) | F1 Score |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Models with conventional risk factors | |||||||||||
| Random forest | 10 | 0.17 | 0.70 (0.70, 0.71) | 0.22 | 1.03 | 0.30 * | 0.98 | 0.04 | 0.65 (0.64, 0.65) | 0.68 | 0.64 |
| Neural network | 10 | 0.19 | 0.72 (0.71, 0.7) | 0.21 | −14.39 | 6.4 × 10−47 | 1.18 | 0.08 | 0.66 (0.65, 0.66) | 0.69 | 0.66 |
| Models with conventional risk factors and genetic liabilities | |||||||||||
| Random forest | 20 | 0.18 | 0.71 (0.71, 0.72) | 0.22 | −5.64 | 1.7 × 10−8 | 1.06 | −0.04 | 0.65 (0.64, 0.65) | 0.68 | 0.65 |
| Neural network | 20 | 0.19 | 0.72 (0.71, 0.72) | 0.21 | −14.44 | 3.0 × 10−47 | 1.18 | 0.07 | 0.66 (0.65, 0.66) | 0.68 | 0.66 |
| Random forest as feature selection method | |||||||||||
| Random forest | 10 | 0.17 | 0.71 (70, 0.71) | 0.22 | 0.10 | 0.92 | 0.99 | −0.04 | 0.65 (0.64, 0.65) | 0.66 | 0.64 |
| Neural network | 10 | 0.18 | 0.72 (0.71, 0.72) | 0.21 | −15.51 | 3.1 × 10−54 | 1.20 | −0.09 | 0.66 (0.65, 0.66) | 0.69 | 0.66 |
| Neural network as feature selection method | |||||||||||
| Random forest | 10 | 0.16 | 0.70 (0.70, 0.71) | 0.22 | −0.44 | 0.66 | 1.00 | −0.04 | 0.64 (0.64, 0.65) | 0.66 | 0.64 |
| Neural network | 10 | 0.17 | 0.71 (0.70, 0.71) | 0.22 | −13.80 | 1.6 × 10−43 | 1.18 | −0.08 | 0.65 (0.65, 0.66) | 0.69 | 0.65 |
| Feature Selection Method | Classification Method | NRI>0 (95% Cl) p-Value | IDI (95% Cl) p-Value |
|---|---|---|---|
| None | * Random forest | Ref | Ref |
| Random forest | Random forest | 0.06 (0.05, 0.08) p-value < 0.00001 | 1.7 × 10−3 (9.0 × 10−4, 2.5 × 10−3) p-value = 1.0 × 10−5 |
| Neural network | Random forest | −0.10 (−0.12, −0.09) p-value < 0.00001 | −0.01 (−9.3 × 10−4, −0.01) p-value < 0.00001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
MacCarthy, G.; Pazoki, R. Using Machine Learning to Evaluate the Value of Genetic Liabilities in the Classification of Hypertension within the UK Biobank. J. Clin. Med. 2024, 13, 2955. https://doi.org/10.3390/jcm13102955
MacCarthy G, Pazoki R. Using Machine Learning to Evaluate the Value of Genetic Liabilities in the Classification of Hypertension within the UK Biobank. Journal of Clinical Medicine. 2024; 13(10):2955. https://doi.org/10.3390/jcm13102955
Chicago/Turabian StyleMacCarthy, Gideon, and Raha Pazoki. 2024. "Using Machine Learning to Evaluate the Value of Genetic Liabilities in the Classification of Hypertension within the UK Biobank" Journal of Clinical Medicine 13, no. 10: 2955. https://doi.org/10.3390/jcm13102955





