A New Method for Anti-Interference Measurement of Capacitance Parameters of Long-Distance Transmission Lines Based on Harmonic Components

Abstract

In the context of strong electromagnetic interference environments, the measurement accuracy of the capacitance parameters of transmission lines under power frequency measurement methods is not high. In this paper, a capacitance parameter anti-interference measurement method for transmission lines based on harmonic components is proposed to overcome the impact of power frequency interference. When applying this method, it is first necessary to open-circuit the end of the line under test. Subsequently, apply voltage to the head end of the tested line through a step-up transformer. Due to the saturation of the transformer during no-load conditions, a large number of harmonics are generated, primarily third harmonic. The third harmonic components of voltage and current on the tested transmission line are extracted using the Fourier transform. The proposed method addresses the influence of line distribution effects by establishing a distributed parameter model for long-distance transmission lines. The relevant transmission matrix for the zero-sequence distributed parameters is obtained by combining Laplace transform and similarity transform to solve the transmission line equations. Using synchronous measurement data from the third harmonic components of voltage and current at both ends of the transmission line, combined with the transmission matrix, this method accurately measures the zero-sequence capacitance parameters. The PSCAD/EMTDC simulation results and field test outcomes have demonstrated the feasibility and accuracy of the proposed method for measuring line capacitance parameters under strong electromagnetic interference.

1. Introduction

As society rapidly develops, the demand for electricity continues to increase, and the transmission network is constantly expanding [1]. The reliable determination of line parameters is critical for power flow calculation, short circuit calculation, stability calculation, relay protection and automation device setting calculation and fault location of a power system [2,3,4,5]. Inaccurate parameters can compromise the safety and stability of power system operation and the accuracy of calculation results. Therefore, obtaining accurate parameters of transmission lines is crucial. However, the challenge lies in the accuracy of these measurements, as the variability and uncertainty inherent in the line environment introduce significant discrepancies in theoretical calculations, rendering them insufficient for practical engineering needs. Therefore, relevant regulations explicitly mandate that transmission line parameters must be obtained in the field [6,7].

During the measurement of transmission line parameters, it is challenging to avoid power frequency interference from nearby normally operating lines [8]. The incremental method is a classic anti-interference measurement technique used in field measurements. It involves applying a power increment to the measuring line by adjusting the power source size and, assuming that interference remains constant for a short period, parameters are calculated using the increments in voltage and current, effectively mitigating the impact of interference [9]. To mitigate the impact of power frequency interference on the measurement of transmission line parameters, the non-power frequency measurement method has been proposed and widely applied in the measurement of transmission line parameters [10]. Reference [11] applies a non-power frequency source and uses Fourier transforms to process the measured non-power frequency signals, then the parameters calculated under the non-power frequency are converted to the power frequency, thereby avoiding the interference from power frequency signals and enhancing accuracy. Reference [12] uses the traditional non-power frequency method to measure the mutual impedance between conductors and the ground impedance, achieving ideal results in field measurements. However, this method only considers power frequency interference caused by an adjacent transmission line and does not account for non-power frequency interference generated on the tested line due to electromagnetic coupling between the adjacent transmission line [13]. Unlike the previously mentioned methods that aim to eliminate interference, the interference method [14] leverages the power frequency interference present on the line under test. This approach transforms a disadvantage into an advantage by utilizing the interference as a measurement power source. The theoretical foundation of the interference method is based on the Thevenin theorem.

The non-power frequency measurement method faces challenges in dealing with strong electromagnetic interference in practical applications. According to [15], for a 20 km 110 kV double-circuit tower, the electrostatic induction voltage is approximately 4–5 kV, and the electromagnetic induction current is around 34–46 A. Similarly, for a 20 km 220 kV double-circuit tower, the electrostatic induction voltage is about 10–13 kV, and the electromagnetic induction current ranges from 110–230 A. In the case of a 50 km 500 kV double-circuit tower, the electrostatic induction voltage is around 30–40 kV, and the electromagnetic induction current is approximately 280–520 A. Furthermore, for a 20 km 220 kV four-circuit tower, the electrostatic induction voltage is about 35–40 kV, and the electromagnetic induction current is approximately 490–600 A. It is evident that, in a strong electromagnetic environment, the intense power frequency interference renders the non-power frequency testing apparatus challenging to apply, posing risks ranging from equipment damage to potential harm to testing personnel.

The landscape of transmission line capacitance parameter measurement is rich with diverse methodologies. Reference [16] pioneers this domain by introducing a super-coupled equation framework, establishing a robust methodology for solving line admittance parameters. This approach utilizes the least-square method within the complex domain to derive precise calculation formulas for admittance parameters, marking a significant advancement in the field. Reference [17] enhances measurement accuracy through a synchronous data collection strategy at both ends of the transmission line, employing the orthogonal distance regression method to estimate the zero-sequence parameters of mutual inductance lines with notable precision. Reference [18] introduces a method for measuring transmission line parameters online using 3D GIS technology. Furthermore, the Wide Area Measurement System (WAMS), based on synchronous phasor measurement technology and Phasor Measurement Units (PMU), has been widely adopted [19,20]. This system provides real-time online measurement of wide-area dynamic information about the electrical grid, offering critical data support for the online evaluation of transmission line parameters. Reference [17] studied the zero-sequence parameter measurement methods for transmission lines based on PMU. However, the above-mentioned measurement methods did not consider the impact of strong electromagnetic interference on capacitance parameter measurements. Reference [21] presents a method based on lumped parameters that utilizes the generation of third harmonic currents by saturated transformers for measurement purposes, and the accuracy of this method has been validated through field measurements on short-distance transmission line, but may lead to significant errors in the capacitance parameter measurement of long-distance transmission lines.

Against this backdrop, this paper proposes a novel anti-interference measurement method to accurately measure the capacitance parameters of long-distance lines. The study creates a precise distributed parameter model and employs Laplace transform and similarity transform methods to derive a set of accurate calculation formulas for zero-sequence distributed capacitance parameters based on the measured voltage and current at both ends of the transmission lines. The proposed approach uses GPS-based synchronous measurement devices to measure the voltage and current at both ends of the transmission lines simultaneously. It uses Fourier algorithm to extract the third harmonic components, which are then utilized to calculate the capacitive parameters. This method can also be extended to measure the distributed capacitance parameters of the transmission lines with more circuits, no longer limited by the number of circuits of the transmission lines. The proposed capacitive parameter measurement method was simulated using PSCAD/EMTDC simulation software (PSCAD 4.6.2), followed by field test. The results from both the simulation and field tests validate the feasibility and accuracy of this harmonic component-based method in resisting industrial frequency interference.

2. Analysis of the Principle of Harmonic Generation in Saturated Transformers

When analyzing transformers under no-load conditions with applied power frequency voltage, core saturation causes the excitation circuit to exhibit non-linear characteristics. This leads to distortion in the excitation current. As saturation increases, the distortion intensifies, manifesting as peaked waveforms, rather than the ideal sinusoidal wave, as shown in Figure 1. Particularly, the positive and negative half-waves of the excitation current are completely symmetrical, mainly containing odd harmonics, especially significant third harmonic components [22].

To measure capacitive parameters, a power frequency voltage is applied to the low-voltage side of the step-up transformer to saturate it, and the high-voltage side is connected to the transmission line. Data is collected using a synchronous measurement device, and harmonics are analyzed through Fourier transform. Capacitance parameters are calculated using the larger amplitude of the third harmonic. This method improves the accuracy and reliability of capacitance parameter measurements, reducing the impact of other interference factors.

In addition, the transformers at both ends of the operating transmission line are usually in a loaded and normal operating state, and one side of the transformer must be connected in a delta configuration. Thus, for transformers on the operating transmission line, their saturation level is much lower than that of no-load transformers on the measurement line. Furthermore, most of the third harmonic components generated by transformers on the operating line are filtered out by their delta-connected side and other harmonic filtering in the power system. Therefore, the interference of third harmonic components brought to the measurement line by the operating transmission line can be completely ignored [23].

3. Anti-Interference Measurement Method for Capacitance Parameters of Long-Distance Transmission Line

In developing distributed parameter models for long-distance transmission lines, this study adopted a series of assumptions, specified the factors ignored, and established particular initial conditions, which include:

1.

Ideal Transposition Assumption: The study assumes that the transmission lines achieve an ideal transposition state, allowing the complex three-phase line model to be simplified to a single-phase model for analysis.

2.

Sinusoidal Steady-State Operating Conditions: It is assumed that the transmission lines operate under sinusoidal steady-state conditions, meaning that the electromagnetic fields are time-harmonic. This allows for the representation of line voltage and current through phasors, thereby simplifying the analysis of electromagnetic parameters.

3.

Ignoring the Influence of Overhead Ground Wires: In analyzing line parameters, the study opts to disregard the potential influence of overhead ground wires, thus reducing computational complexity.

3.1. Anti-Interference Measurement Method for Capacitance Parameters of Long-Distance Single-Circuit Transmission Lines

As the conductance parameters of the lines are very small, they can be ignored. Therefore, the transmission line matrix equation for a single-circuit line is:

$$\left[\begin{array}{c}{\dot{U}}_{s3}\\ {\dot{I}}_{s3}\end{array}\right]=\left[\begin{array}{cc}\cosh (r_{3}l)& z_3\sinh (r_{3}l)\\ \frac{1}{z_3}\sinh (r_{3}l)& \cosh (r_{3}l)\end{array}\right]\left[\begin{array}{c}{\dot{U}}_{m3}\\ {\dot{I}}_{m3}\end{array}\right]$$

(1)

where, $\left\{\begin{array}{l}{r}_3=\sqrt{(R_3+j\omega L_3)j\omega C_3}\\ z_3=\sqrt{\frac{(R_3+j\omega L_3)}{j\omega C_3}}\end{array}\right.$. ${\dot{U}}_{s3}$ and ${\dot{U}}_{m3}$ are the third harmonic zero-sequence voltages at the initial and terminal ends of the line, ${\dot{I}}_{s3}$ and ${\dot{I}}_{m3}$ are the third harmonic zero-sequence currents at the initial and terminal ends of the line. $r_3$, $z_3$ are the transmission coefficient and wave impedance of the line respectively. $R_3$, $L_3$ and $C_3$ are the zero-sequence resistance, zero-sequence inductance, and zero-sequence capacitance under the third harmonic, respectively. $\omega$ is the system angular frequency, and $l$ is the length of the line.

When measuring capacitance parameters, the three-phase at the end of the line under test is left open, and a higher amplitude industrial frequency symmetric voltage source is applied at the beginning of the line via a step-up transformer, hence ${\dot{I}}_{m3}=0$.

The solution to (1) is as follows:

$$\left\{\begin{array}{l}{r}_3=\frac{1}{l}\mathrm{arch}(\frac{{\dot{U}}_{s3}}{{\dot{U}}_{m3}})\\ z_3=\frac{{\dot{U}}_{m3}\sinh (r_{3}l)}{{\dot{I}}_{s3}}\end{array}\right.$$

(2)

Solving (2) yields the power frequency zero-sequence capacitance $C_0$:

$$C_0=\frac{C_3}{3}=\frac{1}{3\omega }\mathrm{imag}(\frac{r_3}{z_3})$$

(3)

3.2. Anti-Interference Measurement Method for Capacitance Parameters of Long-Distance Double-Circuit Transmission Lines

The distributed parameter model for a long-distance double-circuit transmission line is depicted in Figure 2.

In Figure 2, ${\dot{\mathit{U}}}_{\mathit{x}}={\left[{\dot{U}}_{ax}\hspace{1em}{\dot{U}}_{bx}\right]}^T$ represents the terminal voltage on the infinitesimal element dx. $\stackrel{·}{I_x}={\left[\stackrel{·}{I_{ax}}\hspace{1em}\stackrel{·}{I_{bx}}\right]}^T$ represents the terminal current on the infinitesimal element dx. $\mathit{d}{\dot{\mathit{U}}}_{\mathit{x}}={\left[d{\dot{U}}_{ax}\hspace{1em}d{\dot{U}}_{bx}\right]}^T$ represents the voltage drop on the infinitesimal element dx. $\stackrel{·}{d{I}_x}={\left[\stackrel{·}{d{I}_{ax}}\hspace{1em}\stackrel{·}{d{I}_{bx}}\right]}^T$ represents the current drop on the infinitesimal element dx.

The impedance matrix of the double-circuit lines is expressed as follows:

$$Z=\left[\begin{array}{ll}{Z}_{11}& Z_{12}\\ Z_{12}& Z_{22}\end{array}\right]$$

(4)

The admittance matrix of the double-circuit lines is expressed as follows:

$$Y=\left[\begin{array}{cc}{Y}_{11}& -Y_{12}\\ -Y_{12}& Y_{22}\end{array}\right]$$

(5)

where the diagonal elements $Z_{11},Z_{22}$ represent the zero-sequence distributed self-impedance per unit length of the lines, while the off-diagonal element $Z_{12}$ represent the zero-sequence distributed mutual impedance per unit length between two lines. The diagonal elements $Y_{11}, Y_{22}$ represent the distributed self-admittance per unit length of the lines, while the off-diagonal element $Y_{12}$ represent the distributed mutual admittance per unit length between two lines.

The equations of the transmission lines in matrix form are expressed as follows:

$$\frac{d\stackrel{·}{I_x}}{dx}=Y\stackrel{·}{U_x}$$

(6)

$$\frac{d\stackrel{·}{U_x}}{dx}=Z\stackrel{·}{I_x}$$

(7)

The second-order differential equations of Equations (6) and (7) are expressed as follows:

$$\frac{d^2\stackrel{·}{I_x}}{d{x}^2}=YZ\stackrel{·}{I_x}==T\stackrel{·}{I_x}$$

(8)

$$\frac{d^2\stackrel{·}{U_x}}{d{x}^2}=ZY\stackrel{·}{U_x}$$

(9)

In Equation (8), $T=YZ$.

Taking Laplace transform of Equation (8) and substituting the zero-sequence voltage and current at the tail end of the four-circuit lines (the subscript “$m$” indicates the voltage and current data measured at the end of the line), we obtain,

$$\left[\begin{array}{l}{\dot{I}}_{ax}(s)\\ {\dot{I}}_{bx}(s)\end{array}\right]=\frac{s}{s^2\mathit{I}-\mathit{T}}\left[\begin{array}{l}{\dot{I}}_{am}\\ {\dot{I}}_{bm}\end{array}\right]+\frac{\mathit{Y}}{s^2\mathit{I}-\mathit{T}}\left[\begin{array}{l}{\dot{U}}_{am}\\ {\dot{U}}_{bm}\end{array}\right]$$

(10)

In Equation (10), $I$ is a Second-order unit matrix. The value of the determinant of $s^{2}I-T$ is represented as follows,

$$\det (s^2\mathit{I}-\mathit{T})=(s^2-T_1)(s^2-T_4)-T_2{T}_3=(s^2-r_1^2)(s^2-r_2^2)$$

(11)

In Equation (11), $r_1^2,r_2^2$ are the eigenvalues of matrix $T$, respectively.

As stated in [24], the fundamental idea for solving Equations (6) and (7) is to use a similarity transformation to decouple the equations. There exists a matrix $P$, which is composed of the eigenvectors corresponding to the eigenvalues of matrix $T$, such that $P^{-1}TP=\mathsf{\Lambda }=\left[\begin{array}{ll}{r}_1^2\hfill & \hfill 0\\ 0\hfill & \hfill r_2^2\end{array}\right]$.

Taking the inverse Laplace transform of Equation (10) and substituting “$x=l$” (l represents the length of the line), we obtain:

$$\left[\begin{array}{l}{\dot{I}}_{as}\\ {\dot{I}}_{bs}\end{array}\right]=\left[\begin{array}{cc}{A}_1& A_2\\ A_3& A_4\end{array}\right]\left[\begin{array}{l}{\dot{I}}_{am}\\ {\dot{I}}_{bm}\end{array}\right]+\left[\begin{array}{cc}{B}_1& B_2\\ B_3& B_4\end{array}\right]\left[\begin{array}{l}{\dot{U}}_{am}\\ {\dot{U}}_{bm}\end{array}\right]=A\left[\begin{array}{l}{\dot{I}}_{am}\\ {\dot{I}}_{bm}\end{array}\right]+B\left[\begin{array}{l}{\dot{U}}_{am}\\ {\dot{U}}_{bm}\end{array}\right]$$

(12)

In Equation (12), $A=L^{-1}(s{(s^{2}E-T)}^{-1}),B=L^{-1}(Z{(s^{2}E-T)}^{-1})$. Matrix $A$ can be simplified as follows by matrix elementary transformation:

$$\begin{array}{l}A=L^{-1}(s{(s^{2}I-T)}^{-1})=L^{-1}(s{(P{s}^{2}I{P}^{-1}-P\mathsf{\Lambda }{P}^{-1})}^{-1})=L^{-1}(s{(P(s^{2}I-\mathsf{\Lambda })P^{-1})}^{-1})\\ =L^{-1}(sP{(s^{2}I-\mathsf{\Lambda })}^{-1}{P}^{-1})=P{L}^{-1}(s{(s^{2}I-\mathsf{\Lambda })}^{-1})P^{-1}=P\left[\begin{array}{l}\cosh (r_{1}l)\hspace{1em}0\hfill \\ 0\hspace{1em}\cosh (r_{2}l)\hfill \end{array}\right]P^{-1}\end{array}$$

(13)

Similarly, $B=YP\left[\begin{array}{l}\sinh (r_{1}l)/r_1\hspace{1em}0\hfill \\ 0\hspace{1em}\sinh (r_{2}l)/r_2\hfill \end{array}\right]P^{-1}$.

From Equation (13), it can be seen that matrix A shares the same eigenvectors with matrix T, and the eigenvalues of matrix A are $\cosh (r_{1}x),\cosh (r_{2}x)$ respectively.

Similarly, Equation (14) can be obtained by transforming Equation (7).

$$\left[\begin{array}{l}{\dot{U}}_{as}\\ {\dot{U}}_{bs}\end{array}\right]=\left[\begin{array}{cc}{C}_1& C_2\\ C_3& C_4\end{array}\right]\left[\begin{array}{l}{\dot{I}}_{am}\\ {\dot{I}}_{bm}\end{array}\right]+\left[\begin{array}{cc}{D}_1& D_2\\ D_3& D_4\end{array}\right]\left[\begin{array}{l}{\dot{U}}_{am}\\ {\dot{U}}_{bm}\end{array}\right]$$

(14)

In Equation (14), the method of solving matrices and $C$ is $D$ the same as that of matrices $A$ and $B$, and $D=A^T$.

Therefore, a mathematical relationship can be obtained for the relationship between the zero-sequence distributed parameters and the zero-sequence voltage and current at both ends of the double-circuit transmission lines:

$$\left[\begin{array}{l}{\dot{I}}_{as}\\ {\dot{I}}_{bs}\\ {\dot{U}}_{as}\\ {\dot{U}}_{bs}\end{array}\right]=\left[\begin{array}{cccc}{A}_1& A_2& B_1& B_2\\ A_3& A_4& B_3& B_4\\ C_1& C_2& A_1& A_3\\ C_3& C_4& A_2& A_4\end{array}\right]\left[\begin{array}{l}{\dot{I}}_{am}\\ {\dot{I}}_{bm}\\ {\dot{U}}_{am}\\ {\dot{U}}_{bm}\end{array}\right]$$

(15)

For a double-circuit line, during measurement, it is necessary to open-circuit the line at the terminal and successively apply single-phase voltage at the initial end of the line. The two measurement modes are shown in

Table 1. The measurement mode of the double circuit line.

Measurement Modes	Line 1		Line 2
	Head	Tail	Head	Tail
1	Vs	Oc	Oc	Oc
2	Oc	Oc	Vs	Oc

.

In Table 1, “Vs” indicates the higher amplitude industrial frequency symmetric voltage source applied through a step-up transformer, and “Oc” indicates a three-phase open circuit. The GPS-based time synchronization function of the synchronous measurement device ensures that data measured at both ends of the lines are synchronized, meeting the algorithm’s requirement for data synchronization. This paper utilizes the Hanning-windowed FFT algorithm to process two sets of collected voltage and current data from the beginning and end of the line, extracting their third harmonic components.

At this point, where ${\dot{I}}_{am3}={\dot{I}}_{bm3}=0$, substitute the processed third harmonic data into (15) yields Equations (16) and (17). Simultaneously solve Equations (16) and (17) to obtain the coefficients of matrices A and B.

$$\left[\begin{array}{cc}{\dot{U}}_{as3}^1& {\dot{U}}_{as3}^2\\ {\dot{U}}_{bs3}^1& {\dot{U}}_{bs3}^2\end{array}\right]=\left[\begin{array}{cc}{A}_1& A_3\\ A_2& A_4\end{array}\right]\left[\begin{array}{cc}{\dot{U}}_{am3}^1& {\dot{U}}_{am3}^2\\ {\dot{U}}_{bm3}^1& {\dot{U}}_{bm3}^2\end{array}\right]$$

(16)

$$\left[\begin{array}{cc}{\dot{I}}_{as3}^1& {\dot{I}}_{as3}^2\\ {\dot{I}}_{bs3}^1& {\dot{I}}_{bs3}^2\end{array}\right]=\left[\begin{array}{cc}{B}_1& B_2\\ B_3& B_4\end{array}\right]\left[\begin{array}{cc}{\dot{U}}_{am3}^1& {\dot{U}}_{am3}^2\\ {\dot{U}}_{bm3}^1& {\dot{U}}_{bm3}^2\end{array}\right]$$

(17)

We can utilize matrix $A$ to obtain the eigenvalues ${\lambda }_1,{\lambda }_2$ of matrix $A$, as well as matrix $P$ composed of eigenvectors. To obtain the eigenvalues $r_1^2,r_2^2$ of matrix T, we can substitute the eigenvalues of matrix $A$ into Equation (18).

$$\left\{\begin{array}{l}{r}_1^2={\left(\mathrm{arch}\left({\lambda }_1\right)/l\right)}^2\\ r_2^2={\left(\mathrm{arch}\left({\lambda }_2\right)/l\right)}^2\end{array}\right.$$

(18)

Matrix $Y$ can be obtained from Equation (19).

$$Y=BP{\left[\begin{array}{c}\sinh (r_{1}x)/r_1\hspace{1em}0\hfill \\ 0\hspace{1em}\sinh (r_{2}x)/r_2\hfill \end{array}\right]}^{-1}{P}^{-1}$$

(19)

Finally, solve for the measured power frequency zero-sequence capacitance parameters using Equation (20).

$$\left\{\begin{array}{l}{C}_{11}=\frac{\mathrm{imag}(Y_{11})}{3\omega }\\ C_{22}=\frac{\mathrm{imag}(Y_{22})}{3\omega }\\ C_{12}=\frac{\mathrm{imag}(Y_{12})}{3\omega }\end{array}\right.$$

(20)

4. Simulation Validation

4.1. Simulation Analysis of Long-Distance Single-Circuit Line

The simulation model of a long-distance single-circuit line is shown in Figure 3. In Figure 3, the operating line is treated as the equivalent line for all nearby operating lines, which induces power frequency interference in the tested line. When measuring capacitance parameters, the three phases at the end of the line under test are open-circuited, and a higher amplitude power frequency symmetrical voltage source is applied to the first end of the line through a step-up transformer. An open circuit at the end of the line can be equated to an unloaded transformer connected in series with the line. At this time, the higher amplitude voltage source causes the unloaded transformer to enter a saturated state.

In the simulation settings, the sampling frequency was adjusted to 4000 Hz, and the total sampling duration was set to 1 s. For MATLAB R2023a analysis, data from 0.8 s to 0.9 s were selected. In the simulation, the amplitude of the three-phase power supply was set to 1 kV and the transformer turns ratio is 380 V/10 kV, with power frequency zero-sequence capacitance parameter C₀ = 7.5499 nF/km. The tower structure of the tested single-circuit parallel transmission line is detailed in Figure 4.

4.1.1. The Adaptability of the Proposed Method to Line Length

When the length of the line under test is 300 km, the sampled current and voltage waveforms at phase C of the head end of the tested line are shown in Figure 5 and Figure 6, respectively.

The interference line length varies with the tested line, changing the tested line length to obtain simulated measurement results for the zero-sequence capacitance, as shown in

Table 2. Measurement values and relative errors of zero-sequence capacitance distributed parameters of long-distance single-circuit line.

Line Length/km	Zero-Sequence Capacitance C0
	Value (nF/km)	Error/%
200	7.5535	0.0464
300	7.5625	0.1660
400	7.5786	0.3797
500	7.5389	0.1464

.

4.1.2. The Impact of Data Measurement Errors on the Proposed Method

In field measurements, the accuracy classes of instrument transformers are primarily 0.3 and 0.6 [5]. These classes denote measurement errors, indicating that the amplitude and phase errors induced by the instrument transformers do not exceed 0.6% and 0.6 degrees, respectively. Given additional factors in field measurements, this section establishes that the maximum permissible measurement errors for amplitude and phase at the line’s head end are ±1% and ±1°, respectively. Meanwhile, the data at the end of the line are simulated with no errors.

Figure 7 displays the measurement results of zero-sequence capacitance errors when there are measurement errors in the voltage and current data at the beginning of the line (with a line length of 300 km designed in the simulation).

As shown in Figure 7, when there are varying measurement errors in the voltage and current data, the maximum relative error in the measurement results of the proposed method does not exceed 1.2%. Overall, when the errors in the measurement data are within the maximum allowable range, the proposed method continues to maintain high measurement accuracy, meeting the precision requirements of engineering measurements.

4.2. Simulation Analysis of Long-Distance Double-Circuit Line

The simulation model for a double-circuit transmission line is shown in Figure 8. Considering lines 1 and 2 as a whole, at this point, the third harmonic components are generated only by themselves. In Figure 8, the operating line can be considered as the equivalent line for all nearby operating lines, causing power frequency interference to the tested lines 1 and 2. In the simulation, the amplitude of the three-phase power supply was set to 20 kV.

The tower structure of the tested double-circuit parallel transmission line is detailed in Figure 9.

The theoretical values of the zero-sequence capacitance parameters for the double-circuit transmission lines in the simulation model are shown in

Table 3. Theoretical values of zero-sequence capacitance of double-circuit transmission lines.

Zero-Sequence Capacitance (nF/km)
C11	7.6337
C22	7.6337
C12	3.0400

.

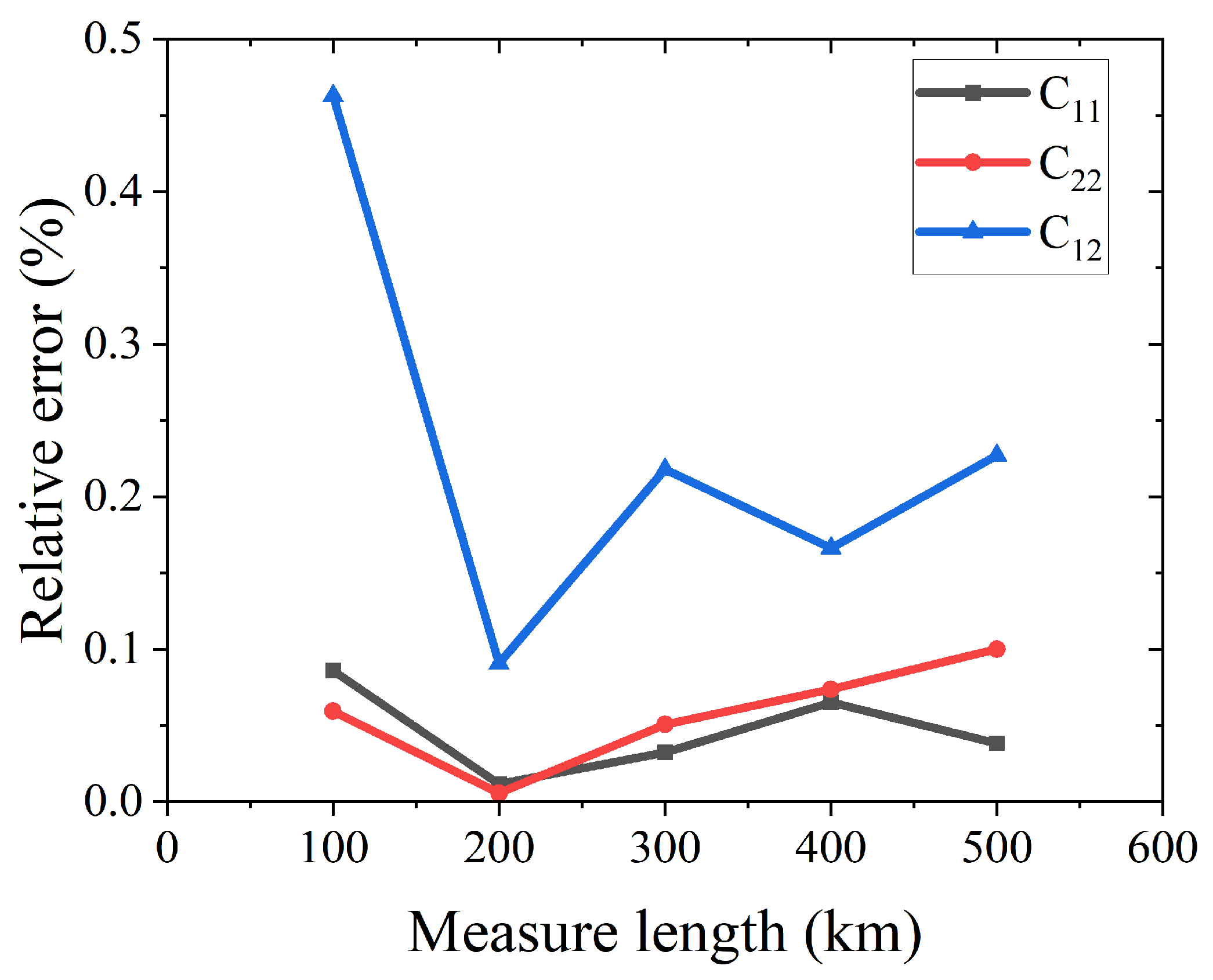
4.2.1. The Adaptability of the Proposed Method to Line Length

When changing the length of the transmission line, the results of this method are shown in

Table 4. Measurement values and relative errors of zero-sequence capacitance distributed parameters of long-distance double-circuit line.

Line Length/km		100	200	300	400	500
C11	Value/(nF/km)	7.6403	7.6328	7.6312	7.6387	7.6308
	Error/%	0.0860	0.0116	0.0324	0.0651	0.0384
C22	Value/(nF/km)	7.6382	7.6333	7.6298	7.6393	7.6413
	Error/%	0.0593	0.0057	0.0507	0.0737	0.1001
C12	Value/(nF/km)	3.0259	3.0428	3.0334	3.0349	3.0469
	Error/%	0.4627	0.0908	0.2179	0.1663	0.2272

. From Table 4, it can be observed that the maximum relative error of the zero-sequence capacitance is 0.4627%.

The relative error of the zero-sequence capacitance selected from Table 4 is compared, as shown in Figure 10.

It can be observed from Figure 10 that the proposed method’s accuracy does not decrease with the increase of the line length, because the proposed method utilizes a distributed parameter model that accounts for the distribution effects of the lines, making the proposed method suitable for the parameter measurement of different lengths of lines.

4.2.2. The Sensitivity of Proposed Method to Variations in the Theoretical Values of Zero Sequence Capacitance Parameter

Transmission lines exhibit different zero-sequence distributed parameter characteristics at various voltage levels. In a simulation study with a line length of 300 km, differences between the theoretical line capacitance parameters and the values listed in Table 3 were observed by modifying the tower structure, split conductors, and soil resistivity in the simulation model. Based on the relative error of the zero-sequence capacitance parameters, the simulation results under different theoretical parameter adjustments are shown in Figure 11.

As illustrated in Figure 11, the method adopted shows extremely low sensitivity to variations in theoretical values, maintaining a high measurement accuracy of no more than 0.45% even with changes in theoretical values. This high level of precision is attributed to meticulous mathematical derivations, which ensure the accurate measurement of zero-sequence distributed parameters. Importantly, the method does not require specific initial parameter settings during the derivation process, demonstrating insensitivity to initial line parameter values. Therefore, this method is well-suited for use in double-circuit transmission lines across various voltage levels.

4.2.3. Influence of Voltage Application Magnitude at the Head End of the Line on the Proposed Method

Gradually increasing the measurement voltage from 10 kV to 30 kV, the zero-sequence capacitance measurement results of the method presented in this paper are depicted in Figure 12. It is observed that the error of this method stays below 0.25% across different voltage applications.

5. Field Test Applications

The schematic diagram of a 220 kV double-circuit transmission line on the same tower in a Chinese power grid is shown in Figure 13.

The 220 kV transmission lines, Line I and Line II, are double-circuited on the same tower, with a length of 47.8 km. When both circuits are de-energized, the zero-sequence capacitance of Line I is measured to be 2.921 × 10⁻⁷ F. In the absence of interference, this measurement is considered accurate.

With Line II operational, the electrostatic induction voltage at the beginning of Line I, when open-ended, is measured at 2184.4 V. This poses challenges to traditional different-frequency testing equipment due to safety concerns for personnel and equipment.

When a power frequency voltage of 14,000 V is applied to the de-energized Line I through a step-up transformer, the waveforms of the zero-sequence voltage and current measured on Line I are presented in Figure 14 and Figure 15, respectively.

The relative error between the zero-sequence capacitance measurements of Line I, based on the power frequency components of zero-sequence voltage and current, and the measurements obtained when the line is completely de-energized, is presented in

Table 5. Zero-sequence capacitance measurement results of Line I based on power frequency quantities and the relative error.

Number of Measurement Times	Measured Power Frequency Zero Sequence Voltage (V)	Measured Power Frequency Zero Sequence Current (A)	Measured Zero Sequence Capacitance (F)	Relative Error (%)
1	10,473.311	1.2069	3.668 × 10−7	25.573
2	12,242.618	1.3892	3.611 × 10−7	23.622
3	14,386.044	1.6121	3.567 × 10−7	22.116
4	14,391.952	1.6117	3.565 × 10−7	22.047

.

The relative error between the zero-sequence capacitance measurements of Line I, based on the third harmonic of zero-sequence voltage and current, and the measurements obtained when the line is completely de-energized, is presented in

Table 6. Zero-sequence capacitance measurement results of Line I based on the third harmonic and the relative error.

Number of Measurement Times	Third Harmonic Voltage (V)	Third Harmonic Current (A)	Measured Zero Sequence Capacitance (F)	Relative Error (%)
1	274.514	0.0857	3.312 × 10−7	13.386
2	330.417	0.1023	3.285 × 10−7	12.461
3	390.370	0.1107	3.008 × 10−7	2.978
4	391.926	0.1108	2.999 × 10−7	2.670

.

In the measurement of the zero-sequence capacitance of a transmission line with an open end using the power frequency method, the short length of the line leads to a very small zero-sequence capacitive current. Despite the application of a zero-sequence voltage of 14,000 V, the zero-sequence current on the line is only approximately 1.6 A. Additionally, the electromagnetic induction effect from the operating line generates a large static induction voltage, exceeding 2000 V, on the tested line. This significantly affects the accuracy of the zero-sequence capacitance measurement of the de-energized line, resulting in a substantial measurement error of over 20%.

To eliminate the influence of power frequency interference, the third harmonic components of zero-sequence voltage and zero-sequence current were used to calculate the zero-sequence capacitance during the measurement. As evidenced by Table 5 and Table 6, when using the third harmonic voltage and third harmonic current to measure the zero-sequence capacitance, the measurement error is less than 14%. When the externally applied zero-sequence power frequency voltage reaches 14,000 V, and the third harmonic voltage reaches 390 V, the relative error between the zero-sequence capacitance measurement results using the third harmonic method and those obtained from a completely de-energized line is below 3%.

Therefore, in the measurement of capacitive parameters of transmission lines, in situations with significant interference voltage, it is advisable to apply a large power frequency voltage and then use the harmonic component method to measure the capacitance of the transmission lines. This approach can significantly improve the accuracy of measuring line capacitive parameters under strong interference conditions.

6. Conclusions and Prospects

6.1. Conclusions

In response to the challenge of measuring the capacitance parameters of transmission lines in environments with strong electromagnetic interference susceptible to power frequency interference, this paper proposes a method for measuring capacitance parameters resistant to power frequency interference based on harmonic components. Through the PSCAD simulation and the field measurement results of the actual line, the following conclusions are obtained:

1.

The proposed method combines Laplace transform and similarity transform methods to measure zero-sequence capacitance distributed parameters of the long-distance transmission lines. The derivation process of the proposed method is independent of the matrix order, making it applicable to the capacitance distributed parameter measurement of multiple-circuit transmission lines.

2.

The capacitance parameter measurement method based on harmonic components effectively overcomes the influence of power frequency interference, thereby improving the accuracy of capacitance parameter measurements for transmission lines.

3.

The method based on harmonic components maintains consistently high measurement accuracy regardless of line length, as it is not affected by the length of the lines.

4.

The sensitivity analysis to the initial values of the parameters shows that the measurement results of the proposed method are independent of the voltage level of the lines, making it applicable for the capacitance parameter measurement of the transmission lines with any voltage level. Moreover, even when changes occur in the line pole structure and environmental factors, adjustments to the initial values of the line parameters still ensure high measurement accuracy.

6.2. Prospect

Although the findings of this paper address some of the deficiencies in the current field of line parameter measurement, the following shortcomings still need improvement:

1.

As this field continues to evolve, one promising direction for future research is the examination of voltage fluctuations and distortions and their impact on line parameter measurement. Recent studies have highlighted the increasing prevalence of such effects in modern electrical networks, often attributed to the influence of power electronic devices [25,26]. When there are no disturbances or in cases of voltage distortion due to higher harmonics, THD measurements conducted by AMI meters align with the Class A power quality analyzer [27]. However, in scenarios of voltage fluctuation—whether the supply voltage is distorted or not—significant inconsistencies appear in the THD measurements between AMI meters and the Class A power quality analyzer [27]. It is crucial to study these factors for the accurate measurement of transmission line parameters. Using three single-axis EF sensors placed on the ground to measure the electric field allows for accurate detection of voltage distortions in each phase [28]. Under voltage fluctuation conditions, the harmonic analysis algorithm based on the Nuttall self-convolution window improved FFT estimates the fundamental frequency amplitude with a relative error three orders of magnitude higher than classical window functions [29]. Therefore, in future studies, this algorithm could replace the windowed FFT method presented in this paper.

2.

This paper has only analyzed the measurement effects on single-circuit and double-circuit transmission lines. It has not examined more complex line models, and variations in measurement outcomes may occur on more complex models, such as non-fully parallel transmission lines. Further research could be conducted in this area in the future.