Predictive Modeling for Microchannel Flow Boiling Heat Transfer under the Dual Effect of Gravity and Surface Modification
Abstract
:1. Introduction
2. Experiments and Results Analysis
2.1. Experimental Apparatus
2.2. Methods of Controlling the Influence of Gravity
2.3. Experimental Data Processing Method
2.4. Experimental Results and Discussion
2.4.1. Experimental Results
2.4.2. Mechanism Analysis
3. New Heat Transfer Model Development and Evaluation
3.1. Evaluation of Existing Heat Transfer Models
3.2. Introduction of New Physical Parameters
3.3. New Developed Heat Transfer Model
3.4. Evaluation of the New Model
4. Conclusions
- By varying the influence of gravity and surface modification on heat transfer in microchannels, the experimental results indicate that the optimal heat transfer performance occurs during horizontal flow with a super-hydrophilic surface, and its average heat transfer coefficients are about 130% and 310% higher than those of the hydrophilic surface and the ordinary surface, respectively. Additionally, a more stable heat transfer performance is observed when gravity is aligned with the flow direction. However, the influence of gravity significantly weakens the surface modification effect, especially for super-hydrophilic modified surfaces. For the super-hydrophilic surface microchannels, their heat transfer performance decreased by about 140% and 130% compared to the horizontal flow condition.
- Through mechanism analysis, it has been confirmed that, in the case of horizontal super- hydrophilic surface microchannels, there is greater surface tension compared to normal and hydrophilic surfaces, promoting fluid flow and bubble formation. Additionally, under the influence of gravity and buoyancy, these bubbles detach from the surface. Hence, it exhibits the best heat transfer performance. However, when vertically oriented, the action of gravity and buoyancy cannot facilitate bubble detachment from the surface, thus leading to a decline in heat transfer performance.
- Among existing heat transfer models, the Kim and Mudawar models have the best prediction accuracy. The prediction errors for the three experiments were conducted using super-hydrophilic surface microchannels with varying degrees of gravity influence. The vertical upward flow, horizontal flow, and vertical downward flow were 36.2%, 45.5%, and 32.6%, respectively. In order to improve the prediction accuracy, we introduced dimensionless numbers and to characterize the effects of gravity and surface modification and established a new flow boiling heat transfer prediction model.
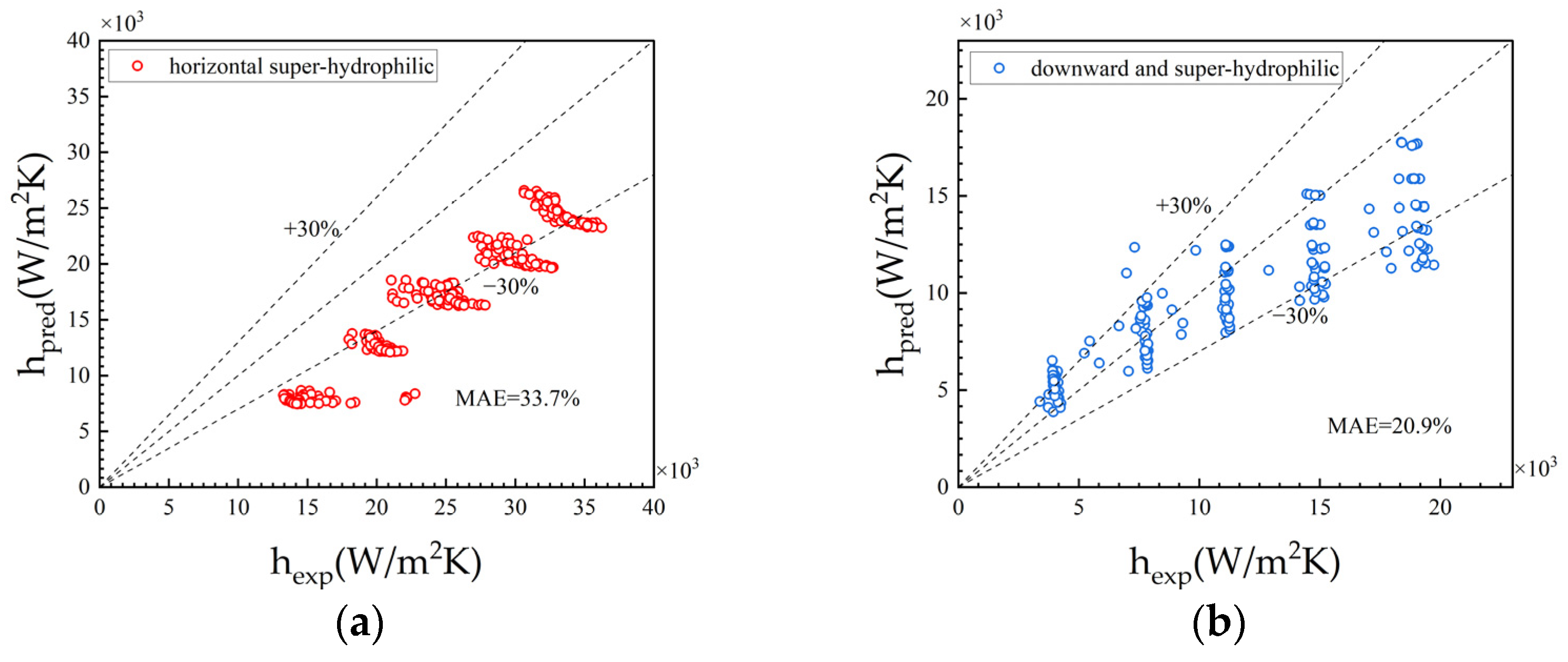
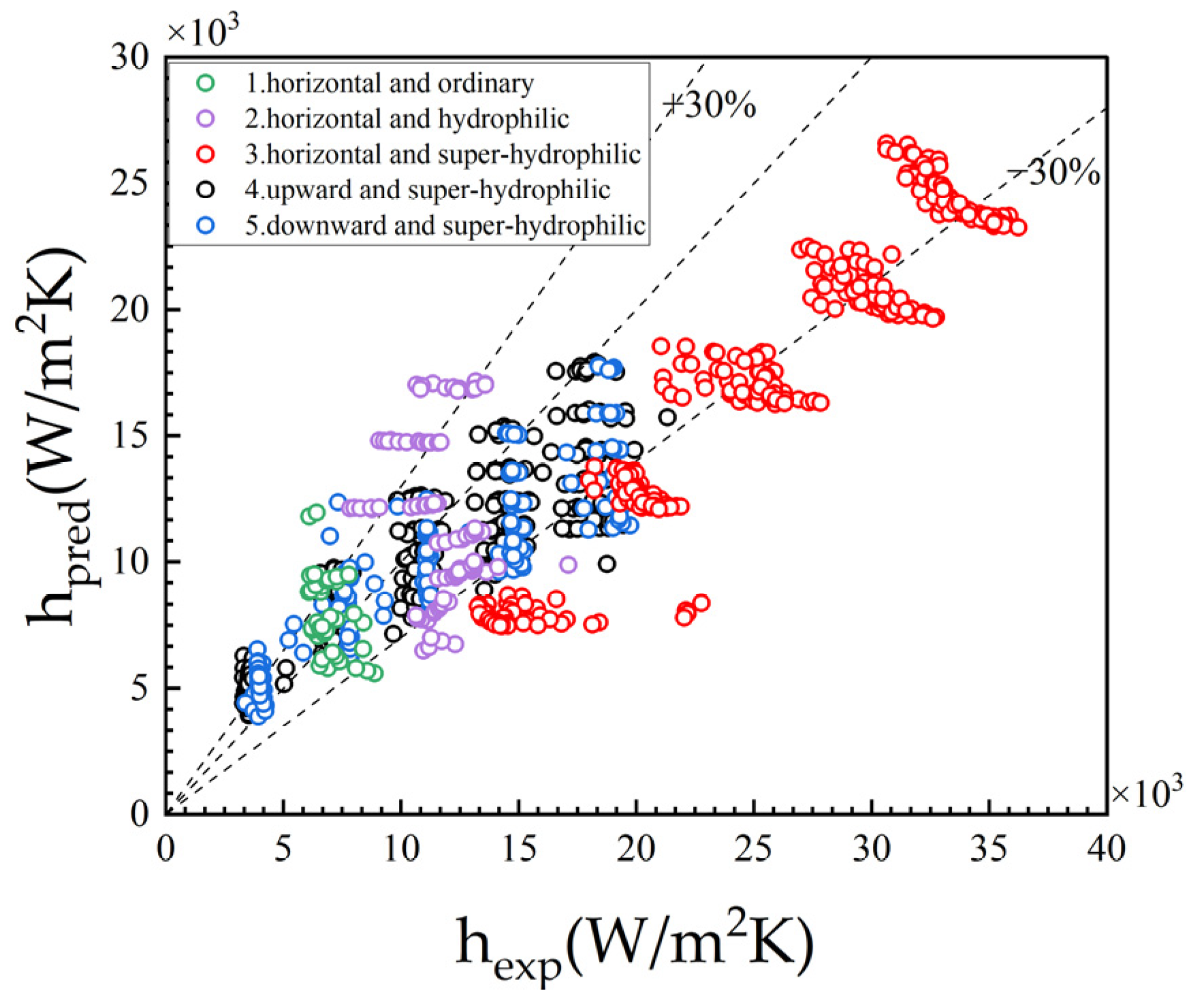
- The new model can effectively predict the flow boiling heat transfer performance of microchannels under different gravity and surface modification conditions. For the super-hydrophilic surface in vertical upward, horizontal, and vertical downward flow, the prediction errors were 21.4%, 33.7%, and 20.9%, respectively. Compared with the best existing model, the prediction errors were reduced by 12–15%. The application scope of the new model has also been expanded. Furthermore, there is still room for improvement in the model expressed in power function form.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Nomenclature | |
| , Bond number [-] | |
| , boiling number [-] | |
| confinement number [-] | |
| hydraulic diameter [mm] | |
| E factor [-] | |
| F factor [-] | |
| Fang number [-] | |
| , Froude number [-] | |
| mass flux [kg/m2s] | |
| gravitational acceleration [m/s2] | |
| average heat transfer coefficient [kW/m2K] | |
| fluid enthalpy in storage tank [kJ/kg] | |
| inlet fluid enthalpy [kJ/kg] | |
| inlet latent heat of vaporization [kJ/kg] | |
| latent heat of vaporization at a given position [kJ/kg] | |
| , Jacob number [-] | |
| thermal conductivity [W/m K] | |
| channel length [mm] | |
| mean absolute error [-] | |
| mass flow rate [kg/s] | |
| heating power in preheating section [W] | |
| wetted perimeter of channel [m] | |
| heated perimeter of channel [m] | |
| reduced pressure [-] | |
| , Prandtl number [-] | |
| heating power in test section [W] | |
| effective heat flux density [kW/m2] | |
| , Reynolds number [-] | |
| Temperature [°C] | |
| , Webb number [-] | |
| vapor quality [-] | |
| Lockhart–Martinelli parameter based on turbulent liquid-turbulent vapor flows [-] | |
| , Y parameter [-] | |
| coordinate along microchannel [m] | |
| density [kg/m3] | |
| dynamic viscosity [N·s/m2] | |
| surface tension [N/m] | |
| , dimensionless flow parameter [-] | |
| contact angle [°] | |
| surface energy parameter [N/m] | |
| Subscript | |
| convective boiling dominant heat transfer | |
| experimental | |
| saturated liquid | |
| liquid only | |
| saturated vapor | |
| inlet | |
| liquid | |
| new modified | |
| nucleate boiling dominant heat transfer | |
| predicted | |
| solid | |
| saturation | |
| single-phase | |
| test section | |
| two-phase | |
| wall | |
| coordinate along microchannel |
References
- Mudawar, I. Two-Phase Microchannel Heat Sinks: Theory, Applications, and Limitations. J. Electron. Packag. 2011, 133, 041002. [Google Scholar] [CrossRef]
- Valeh-e-Sheyda, P.; Rahimi, M.; Karimi, E.; Asadi, M. Application of Two-Phase Flow for Cooling of Hybrid Microchannel PV Cells: A Comparative Study. Energy Convers. Manag. 2013, 69, 122–130. [Google Scholar] [CrossRef]
- Oliet, C.; Oliva, A.; Castro, J.; Perez-Segarra, C.D. Parametric Studies on Automotive Radiators. Appl. Therm. Eng. 2007, 27, 2033–2043. [Google Scholar] [CrossRef]
- Mudawar, I. Recent Advances in High-Flux, Two-Phase Thermal Management. J. Therm. Sci. Eng. Appl. 2013, 5, 021012. [Google Scholar] [CrossRef]
- Fang, Y.; Zhang, Z.; Xu, D.; Wang, Y.; Yang, H.; Huang, Y. Experimental Investigation on Flow Pattern and Bubble Behavior during Subcooled Flow Boiling of R1233zd(E) in Parallel Channels. J. Therm. Sci. 2023, 32, 2374–2385. [Google Scholar] [CrossRef]
- Subramanian, M.; Hoang, A.T.; B, K.; Nižetić, S.; Solomon, J.M.; Balasubramanian, D.; C, S.; G, T.; Metghalchi, H.; Nguyen, X.P. A Technical Review on Composite Phase Change Material Based Secondary Assisted Battery Thermal Management System for Electric Vehicles. J. Clean. Prod. 2021, 322, 129079. [Google Scholar] [CrossRef]
- Liu, P.; Guo, Y.; Ding, W.; Tang, M.; Song, Y.; Peng, X.; Ji, J.; Chen, Q.; Mao, X. Critical Heat Flux (CHF) Correlations for Subcooled Water Flow Boiling at High Pressure and High Heat Flux. J. Therm. Sci. 2021, 30, 279–293. [Google Scholar] [CrossRef]
- Liang, G.; Mudawar, I. Review of Channel Flow Boiling Enhancement by Surface Modification, and Instability Suppression Schemes. Int. J. Heat Mass Transf. 2020, 146, 118864. [Google Scholar] [CrossRef]
- Yang, Q.; Shu, B.; Wang, J.; Guo, Y. Experimental Investigation on Flow Boiling Heat Transfer and Flow Patterns in a Single Micro-Channel with Large Mass Velocity. Exp. Therm. Fluid Sci. 2018, 91, 283–291. [Google Scholar] [CrossRef]
- Shi, Q.; Shu, B.; Jiang, J.; Zhang, Y. Effect of Optical–Electrical–Thermal Coupling on the Performance of High-Concentration Multijunction Solar Cells. Appl. Sci. 2022, 12, 5888. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, H.; Li, M.; Liu, H.; Huang, J. Experimental Investigation of a Novel LCPV/T System with Micro-Channel Heat Pipe Array. Renew. Energy 2018, 115, 773–782. [Google Scholar] [CrossRef]
- Karayiannis, T.G.; Mahmoud, M.M. Flow Boiling in Microchannels: Fundamentals and Applications. Appl. Therm. Eng. 2017, 115, 1372–1397. [Google Scholar] [CrossRef]
- Zhang, G.; Kandlikar, S.G. A Critical Review of Cooling Techniques in Proton Exchange Membrane Fuel Cell Stacks. Int. J. Hydrog. Energy 2012, 37, 2412–2429. [Google Scholar] [CrossRef]
- Tran, T.N.; Chyu, M.C.; Wambsganss, M.W.; France, D.M. Two-Phase Pressure Drop of Refrigerants during Flow Boiling in Small Channels: An Experimental Investigation and Correlation Development. Int. J. Multiph. Flow 2000, 26, 1739–1754. [Google Scholar] [CrossRef]
- Size Effect on Two-Phase Regime for Condensation in Micro/Mini Tubes. Available online: https://www.webofscience.com/wos/alldb/full-record/INSPEC:7600318 (accessed on 27 November 2022).
- Jothi Prakash, C.G.; Prasanth, R. Enhanced Boiling Heat Transfer by Nano Structured Surfaces and Nanofluids. Renew. Sustain. Energy Rev. 2018, 82, 4028–4043. [Google Scholar] [CrossRef]
- Liu, T.Y.; Li, P.L.; Liu, C.W.; Gau, C. Boiling Flow Characteristics in Microchannels with Very Hydrophobic Surface to Super-Hydrophilic Surface. International J. Heat Mass Transf. 2011, 54, 126–134. [Google Scholar] [CrossRef]
- Choi, C.; Shin, J.S.; Yu, D.I.; Kim, M.H. Flow Boiling Behaviors in Hydrophilic and Hydrophobic Microchannels. Exp. Therm. Fluid Sci. 2011, 35, 816–824. [Google Scholar] [CrossRef]
- Azizifar, S.; Ameri, M.; Behroyan, I. An Experimental Study of Subcooled Flow Boiling of Water in the Horizontal and Vertical Direction of a Metal-Foam Tube. Therm. Sci. Eng. Prog. 2020, 20, 100748. [Google Scholar] [CrossRef]
- Devahdhanush, V.S.; Mudawar, I.; Nahra, H.K.; Balasubramaniam, R.; Hasan, M.M.; Mackey, J.R. Experimental Heat Transfer Results and Flow Visualization of Vertical Upflow Boiling in Earth Gravity with Subcooled Inlet Conditions—In Preparation for Experiments Onboard the International Space Station. Int. J. Heat Mass Transf. 2022, 188, 122603. [Google Scholar] [CrossRef]
- Konishi, C.; Mudawar, I.; Hasan, M.M. Investigation of the Influence of Orientation on Critical Heat Flux for Flow Boiling with Two-Phase Inlet. Int. J. Heat Mass Transf. 2013, 61, 176–190. [Google Scholar] [CrossRef]
- Saisorn, S.; Wongpromma, P.; Wongwises, S. The Difference in Flow Pattern, Heat Transfer and Pressure Drop Characteristics of Mini-Channel Flow Boiling in Horizontal and Vertical Orientations. Int. J. Multiph. Flow 2018, 101, 97–112. [Google Scholar] [CrossRef]
- Gao, W.; Xu, X.; Liang, X. Experimental Study on the Effect of Orientation on Flow Boiling Using R134a in a Mini-Channel Evaporator. Appl. Therm. Eng. 2017, 121, 963–973. [Google Scholar] [CrossRef]
- Kaya, A.; Lecompte, S.; De Paepe, M. Experimental Flow Boiling Study of R245a at High Reduced Pressures in a Large Diameter Horizontal Tube. Energies 2022, 15, 864. [Google Scholar] [CrossRef]
- Balasubramanian, K.R.; Peter, R.J.; Krishnan, R.A. Recent Hypotheses on the Parameters of Microchannel Flow Boiling: A Comprehensive Overview. Microfluid. Nanofluid. 2022, 26, 80. [Google Scholar] [CrossRef]
- Li, W.; Chen, Z.; Li, J.; Sheng, K.; Zhu, J. Subcooled Flow Boiling on Hydrophilic and Super-Hydrophilic Surfaces in Microchannel under Different Orientations. Int. J. Heat Mass Transf. 2019, 129, 635–649. [Google Scholar] [CrossRef]
- Li, J.; Lin, Y.; Li, W.; Zhou, K. Local Heat Transfer of Saturated Flow Boiling in Vertical Narrow Microchannel. J. Heat Transf. 2020, 142, 071601. [Google Scholar] [CrossRef]
- Li, W.; Ma, J.; Alam, T.; Yang, F.; Khan, J.; Li, C. Flow Boiling of HFE-7100 in Silicon Microchannels Integrated with Multiple Micro-Nozzles and Reentry Micro-Cavities. Int. J. Heat Mass Transf. 2018, 123, 354–366. [Google Scholar] [CrossRef]
- Ren, C.; Li, W.; Ma, J.; Huang, G.; Li, C. Flow Boiling in Microchannels Enhanced by Parallel Microgrooves Fabricated on the Bottom Surfaces. Int. J. Heat Mass Transf. 2021, 166, 120756. [Google Scholar] [CrossRef]
- Zhou, S.; Shu, B.; Yu, Z.; Huang, Y.; Zhang, Y. Experimental Study and Mechanism Analysis of the Flow Boiling and Heat Transfer Characteristics in Microchannels with Different Surface Wettability. Micromachines 2021, 12, 881. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, H.; Zhang, L.; Yang, Y.; Niu, X.; Zeng, Z.; Shu, B. Flow Pattern Study and Pressure Drop Prediction of Two-Phase Boiling Process in Different Surface Wettability Microchannel. Micromachines 2023, 14, 958. [Google Scholar] [CrossRef]
- rieu Phan, H.; Caney, N.; Marty, P.; Colasson, S.; Gavillet, J. Flow Boiling of Water on Nanocoated Surfaces in a Microchannel. J. Heat Transf. 2012, 134, 020901. [Google Scholar] [CrossRef]
- Zhou, K.; Coyle, C.; Li, J.; Buongiorno, J.; Li, W. Flow Boiling in Vertical Narrow Microchannels of Different Surface Wettability Characteristics. Int. J. Heat Mass Transf. 2017, 109, 103–114. [Google Scholar] [CrossRef]
- Bower, J.S.; Klausner, J.F. Gravity Independent Subcooled Flow Boiling Heat Transfer Regime. Exp. Therm. Fluid Sci. 2006, 31, 141–149. [Google Scholar] [CrossRef]
- Lazarek, G.M.; Black, S.H. Evaporative Heat Transfer, Pressure Drop and Critical Heat Flux in a Small Vertical Tube with R-113. Int. J. Heat Mass Transf. 1982, 25, 945–960. [Google Scholar] [CrossRef]
- Schrock, V.E.; Grossman, L.M. Forced Convection Boiling in Tubes. Nucl. Sci. Eng. 1962, 12, 474–481. [Google Scholar] [CrossRef]
- Gungor, K.E.; Winterton, R.H.S. Simplified General Correlation for Saturated Flow Boiling and Comparison with Data. Chem. Eng. Res. Des. 1987, 65, 148–156. [Google Scholar]
- Kim, S.-M.; Mudawar, I. Universal Approach to Predicting Saturated Flow Boiling Heat Transfer in Mini/Micro-Channels—Part II. Two-Phase Heat Transfer Coefficient. Int. J. Heat Mass Transf. 2013, 64, 1239–1256. [Google Scholar] [CrossRef]
- Fang, X. A New Correlation of Flow Boiling Heat Transfer Coefficients for Carbon Dioxide. Int. J. Heat Mass Transf. 2013, 64, 802–807. [Google Scholar] [CrossRef]
- Zhu, D.-Y.; Dai, P.-Q.; Luo, X.-B.; Zhang, Y.-C. Novel Characterization of Wetting Properties and the Calculation of Li2id-Solid Interface Tension(I). Sci. Technol. Eng. 2007, 7, 3057–3062. [Google Scholar]













| Parameter | Dimensions |
|---|---|
| Number of channels | 3 |
| Channel length/mm | 78 |
| Channel width/mm | 1.6 |
| Channel depth/mm | 0.6 |
| /mm | 0.872 |
| Parameter | Range | Unit |
|---|---|---|
| Mass flux | 735–1271 × 103 | |
| Heat flux density | 9–46 × 103 | |
| Inlet vapor quality | 0.018–0.182 |
| Parameter | Uncertainty |
|---|---|
| Pressure | 0.7% |
| Pressure drop | 1.0% |
| Wall temperature | 0.5 °C |
| Fluid temperature | 0.5 °C |
| Heat flux | 0.5% |
| Mass flux | 0.5% |
| Vapor quality | 7.2% |
| Local heat transfer coefficient | 12.5% |
| Average heat transfer coefficient | 12.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Zhou, S.; Wang, D.; Yang, Y.; Liu, L.; Mao, H.; Shu, B. Predictive Modeling for Microchannel Flow Boiling Heat Transfer under the Dual Effect of Gravity and Surface Modification. Processes 2024, 12, 1028. https://doi.org/10.3390/pr12051028
Wu H, Zhou S, Wang D, Yang Y, Liu L, Mao H, Shu B. Predictive Modeling for Microchannel Flow Boiling Heat Transfer under the Dual Effect of Gravity and Surface Modification. Processes. 2024; 12(5):1028. https://doi.org/10.3390/pr12051028
Chicago/Turabian StyleWu, Haoxian, Shengnan Zhou, Dongwei Wang, Yunbo Yang, Linglin Liu, Huijie Mao, and Bifen Shu. 2024. "Predictive Modeling for Microchannel Flow Boiling Heat Transfer under the Dual Effect of Gravity and Surface Modification" Processes 12, no. 5: 1028. https://doi.org/10.3390/pr12051028





