Sensitivity of a Process for Heating Thin Metal Film Described by the Dual-Phase Lag Equation with Temperature-Dependent Thermophysical Parameters to Perturbations of Lag Times
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mathematical Description of the Process
2.2. Sensitivity Models
2.3. Method of Solution
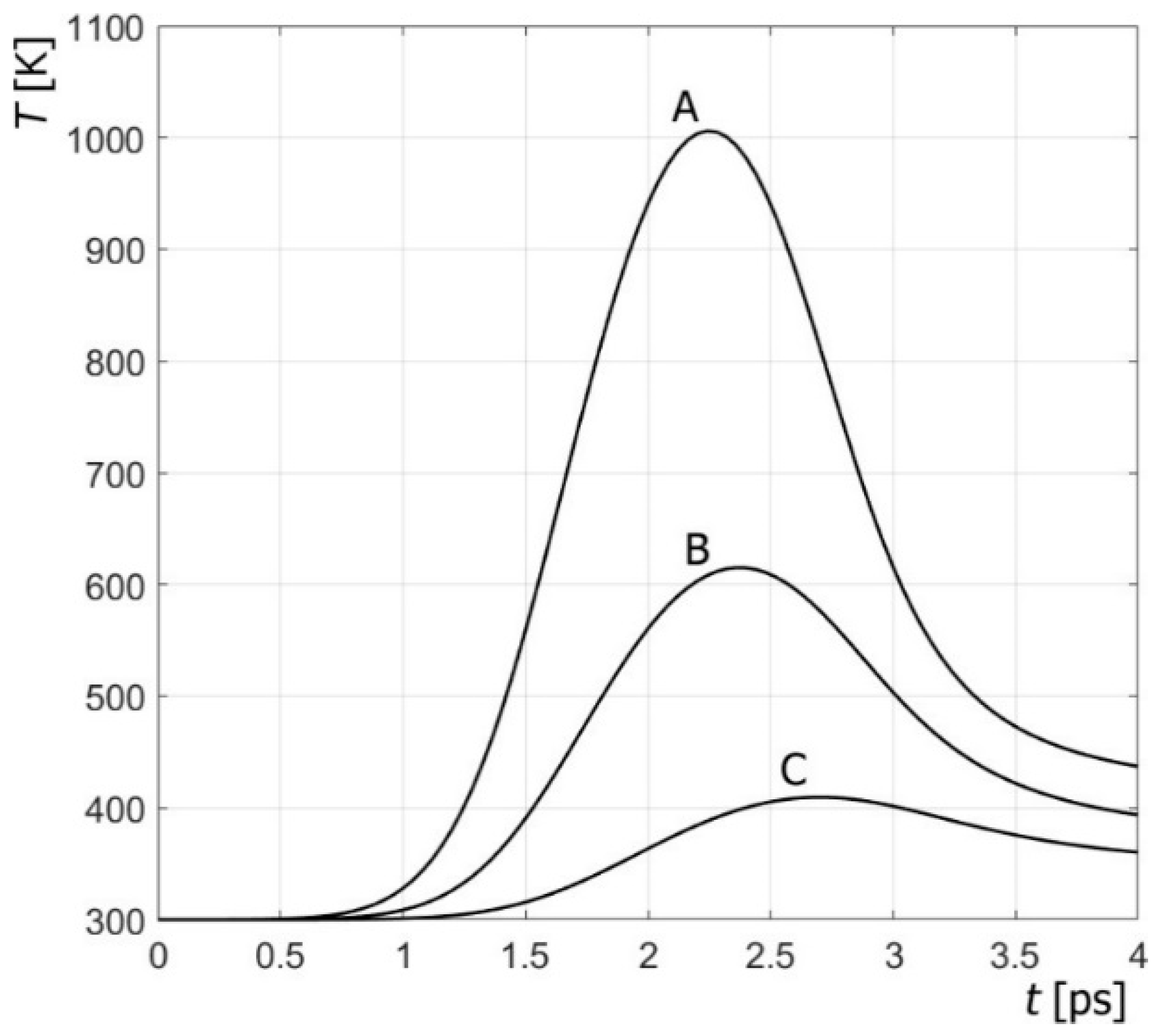
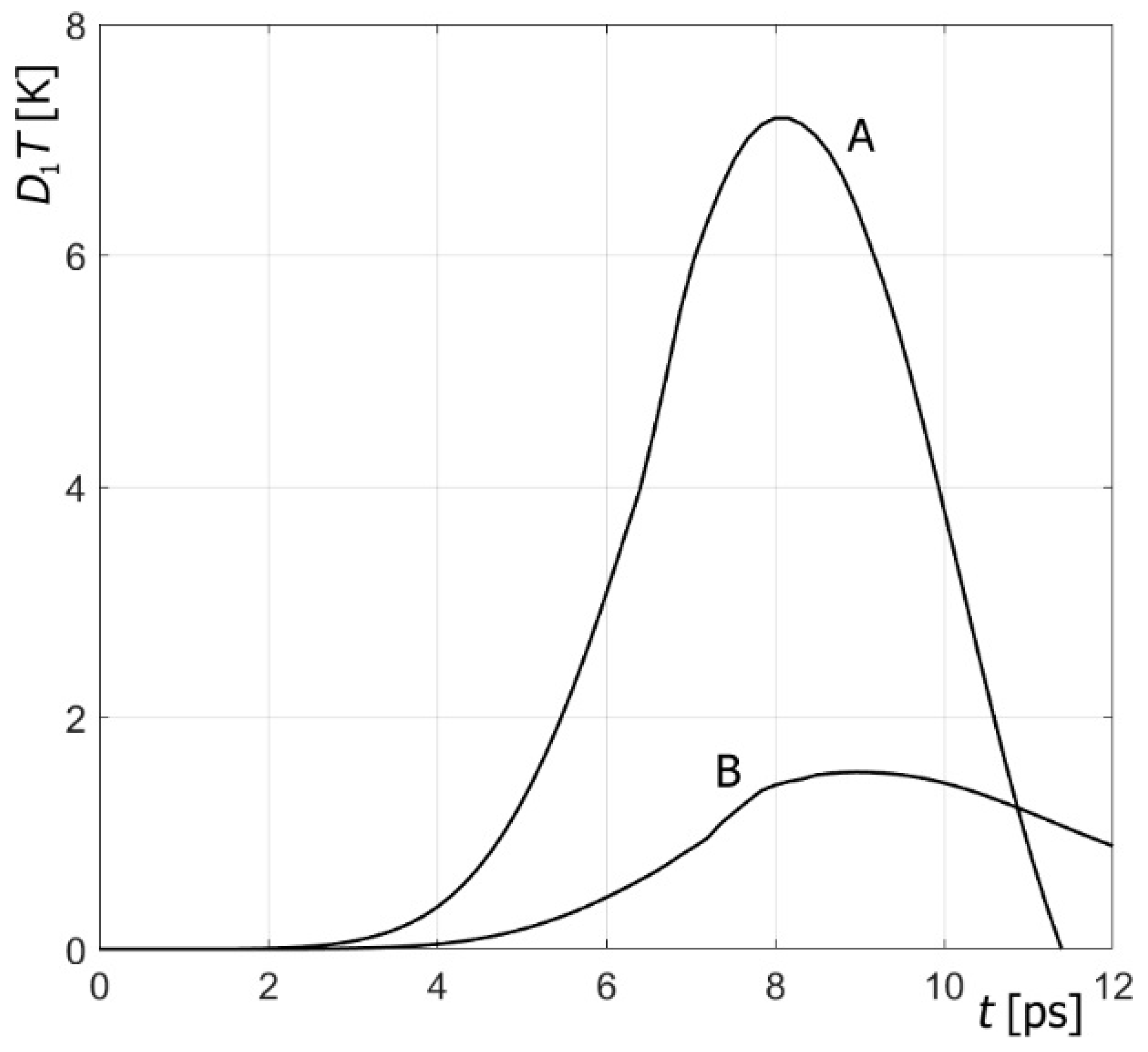
3. Results of Computations and Their Discussion
4. Conclusions
- -
- taking into account the variability of thermophysical parameters (especially for higher temperatures) causes visible changes in the results of numerical simulations;
- -
- disturbances in the delay-time values clearly change the course of the heating/cooling process in the domain considered;
- -
- the sensitivity of the temperature field with respect to the delay times increases with the increase in laser intensity;
- -
- the sensitivity of the temperature field with respect to the delay times varies depending on the type of material and is greater when the metal has a higher mean conductivity coefficient and a lower mean volumetric specific heat.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Majchrzak, E.; Mochnacki, B. Modelling of thin metal film heating using the dual-phase lag equation with temperature-dependent parameters. Int. J. Heat Mass Transf. 2023, 209, 124088. [Google Scholar] [CrossRef]
- Alexopoulou, V.E.; Markopoulos, A.P. A Markopoulos, A critical assessment regarding two-temperature models: An investigation of the different forms of two-temperature models, the various ultrashort pulsed laser models and computational methods. Arch. Comput. Methods Eng. 2023, 31, 93–123. [Google Scholar] [CrossRef]
- Majchrzak, E.; Dziatkiewicz, J.; Turchan, L. Analysis of thermal processes occuring in the microdomain subjected to the ultrashort laser pulse using the axisymmetric two-temperature model. Int. J. Multiscale Comput. Eng. 2017, 15, 395–411. [Google Scholar] [CrossRef]
- Sobolev, S. Nonlocal two-temperature model: Application to heat transport in metals irradiated by ultrashort laser pulses. Int. J. Heat Mass Transf. 2016, 94, 138–144. [Google Scholar] [CrossRef]
- Majchrzak, E.; Mochnacki, B.; Greer, A.; Suchy, J.S. Numerical modeling of short pulse laser interactions with multi-layered thin metal films. CMES Comput. Model. Eng. Sci. 2009, 41, 131–146. [Google Scholar]
- Smith, A.N.; Norris, P.M. Microscale Heat Transfer. In Heat Transfer Handbook; John Willey & Sons: Hoboken, NJ, USA, 2003; Chapter 18. [Google Scholar]
- Zhang, Z.M. Nano/Microscale Heat Transfer; McGraw-Hill: New York, NY, USA, 2007. [Google Scholar]
- Tzou, D.Y. Macro- to Microscale Heat Transfer: The Lagging Behavior; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2015. [Google Scholar]
- Cattaneo, M.C. A form of heat conduction equation which eliminates the paradox of instantaneous propagation. Compte. Rendus. 1958, 247, 431–433. [Google Scholar]
- Askarizadeh, H.; Baniasadi, E.; Ahmadikia, H. Equilibrium and non-eqilibrium thermodynamic analysis of high-order dual-phase-lag heat conduction. Int. J. Heat Mass Transf. 2017, 104, 301–309. [Google Scholar] [CrossRef]
- Deng, D.; Jiang, Y.; Liang, D. High-order finite difference method for a second order dual-phase-lagging models of microscale heat transfer. Appl. Math. Comput. 2017, 309, 31–48. [Google Scholar] [CrossRef]
- Majchrzak, E.; Mochnacki, B. Second-order dual phase-lag equation. Modeling of melting and resolidification of thin metal film subjected to a laser pulse. Mathematics 2020, 8, 999. [Google Scholar] [CrossRef]
- Chiriţă, S.; Ciarletta, M.; Tibullo, V. On the thermomechanical consistency of the time differential dual-phase-lag models of heat conduction. Int. J. Heat Mass Transf. 2017, 114, 277–285. [Google Scholar] [CrossRef]
- Ciesielski, M.; Mochnacki, B.; Majchrzak, E. Integro-differential form of the first-order dual phase lag heat transfer equation and its numerical solution using the Control Volume Method. Arch. Mech. 2020, 72, 415–444. [Google Scholar]
- Xu, H.-Y.; Jiang, X.-Y. Time fractional dual-phase-lag heat conduction equation. Chin. Phys. B 2015, 24, 034401. [Google Scholar] [CrossRef]
- Kukla, S.; Siedlecka, U.; Ciesielski, M. Fractional order dual-phase-lag model of heat conduction in a composite spherical medium. Materials 2022, 15, 7251. [Google Scholar] [CrossRef]
- Azhdari, M.; Seyedpour, S.M.; Lambers, L.; Tautenhahn, H.-M.; Tautenhahn, F.; Ricken, T.; Rezazadeh, G. Non-local three phase lag bio thermal modeling of skin tissue and experimental evaluation. Int. Commun. Heat Mass Transf. 2023, 149, 107146. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, Y.; Yang, J. Bio-heat response of skin tissue based on three-phase-lag model. Sci. Rep. 2020, 10, 16421. [Google Scholar] [CrossRef]
- Chiriţă, S. High-order effects of thermal lagging in deformable conductors. Int. J. Heat Mass Transf. 2018, 127, 965–974. [Google Scholar] [CrossRef]
- Quintanilla, R.; Racke, R. A note on stability in dual-phase-lag heat conduction. Int. J. Heat Mass Transf. 2006, 49, 1209–1213. [Google Scholar] [CrossRef]
- Arefmanesh, A.; Arani, A.A.A.; Emamifar, A. Semi-analytical solutions for different non-linear models of dual phase lag equation in living tissues. Int. Commun. Heat Mass Transf. 2020, 115, 104596. [Google Scholar] [CrossRef]
- Majchrzak, E.; Stryczyński, M. Numerical analysis of biological tissue heating using the dual-phase lag equation with temperature—Dependent parameters. J. Appl. Math. Comput. Mech. 2022, 21, 85–98. [Google Scholar] [CrossRef]
- Kumar, R.; Vashishth, A.; Ghangas, S. Phase-lag effects in skin tissue during transient heating. Int. J. Appl. Mech. Eng. 2019, 24, 603–623. [Google Scholar] [CrossRef]
- Afrin, N.; Zhou, J.; Zhang, Y.; Tzou, D.Y.; Chen, J.K. Numerical simulation of thermal damage to living biological tissues induced by laser irradiation based on a generalized dual phase lag model. Numer. Heat Transfer Part A Appl. 2012, 61, 483–501. [Google Scholar] [CrossRef]
- Shomali, Z.; Kovács, R.; Ván, P.; Kudinov, I.V.; Ghazanfarian, J. Lagging heat models in thermodynamics and bioheat transfer: A critical review. Contin. Mech. Thermodyn. 2022, 34, 637–679. [Google Scholar] [CrossRef]
- Ramadan, K. Semi-analytical solutions for the dual phase lag heat conduction in multi-layered media. Int. J. Therm. Sci. 2009, 48, 14–25. [Google Scholar] [CrossRef]
- Ciesielski, M. Analytical solution of the dual phase lag equation describing the laser heating of thin metal film. J. Appl. Math. Comput. Mech. 2017, 16, 33–40. [Google Scholar] [CrossRef]
- Mohammadi-Fakhar, V.; Momeni-Masuleh, S. An approximate analytic solution of the heat conduction equation at nanoscale. Phys. Lett. A 2010, 374, 595–604. [Google Scholar] [CrossRef]
- Ma, J.; Sun, Y.; Yang, J. Analytical solution of dual-phase-lag heat conduction in a finite medium subjected to a moving heat source. Int. J. Therm. Sci. 2018, 125, 34–43. [Google Scholar] [CrossRef]
- Kumar, S.; Srivastava, A. Finite integral transform-based analytical solutions of phase lag bio-heat transfer equation. Appl. Math. Model. 2017, 52, 378–403. [Google Scholar] [CrossRef]
- Yang, W.; Pourasghar, A.; Cui, Y.; Wang, L.; Chen, Z. Transient heat transfer analysis of a cracked stip irradiated by ultrafast Gaussian laser beam using dual-phase-lag theory. Int. J. Heat Mass Transf. 2023, 203, 123771. [Google Scholar] [CrossRef]
- Dutta, J.; Biswas, R.; Kundu, B. Analytical solution of dual-phase-lag based heat transfer model in ultrashort pulse laser heating of A6061 and Cu3Zn2 nano film. Opt. Laser Technol. 2020, 128, 106207. [Google Scholar] [CrossRef]
- Wang, H.; Dai, W.; Melnik, R. A finite difference method for studying thermal deformation in a double-layered thin film exposed to ultrashort pulsed lasers. Int. J. Therm. Sci. 2006, 45, 1179–1196. [Google Scholar] [CrossRef]
- Chen, J.K.; Beraun, J.E. Numerical study of ultrashort laser pulse interactions with metal films. Numer. Heat Transfer Part A Appl. 2001, 40, 1–20. [Google Scholar] [CrossRef]
- Saeed, T.; Abbas, I. Finite element analyses of nonlinear DPL bioheat model in spherical tissues using experimental data. Mech. Based Des. Struct. Mach. 2022, 50, 1287–1297. [Google Scholar] [CrossRef]
- Kumar, D.; Rai, K. A study on thermal damage during hyperthermia treatment based on DPL model for multilayer tissues using finite element Legendre wavelet Galerkin approach. J. Therm. Biol. 2016, 62, 170–180. [Google Scholar] [CrossRef] [PubMed]
- Majchrzak, E.; Turchan, L. Modeling of laser heating of bi-layered microdomain using the general boundary element method. Eng. Anal. Bound. Elements 2019, 108, 438–446. [Google Scholar] [CrossRef]
- Kleiber, M. Parameter Sensitivity in Non-Linear Mechanics; John Willey & Sons Ltd.: London, UK, 1997. [Google Scholar]
- Dems, K.; Rousselet, B. Rousselet, Sensitivity analysis for transient heat conduction in a solid body, Part I. Struct. Optim. 1999, 17, 36–45. [Google Scholar] [CrossRef]
- Majchrzak, E.; Kałuża, G. Sensitivity analysis of temperature in heated soft tissues with respect to time delays. Contin. Mech. Thermodyn. 2022, 34, 587–599. [Google Scholar] [CrossRef]
- Hector, L.G.; Woo-Seung, K.; Özisik, M. Propagation and reflection of thermal waves in a finite medium due to axisymmetric surface sources. Int. J. Heat Mass Transf. 1992, 35, 897–912. [Google Scholar] [CrossRef]
- Grigoropoulos, C.P.; Chimmalgi, A.C.; Hwang, D.J. Nano-Structuring Using Pulsed Laser Irradiation, Laser Ablation and Its Applications; Springer Series in Optical Sciences; Springer: Boston, MA, USA, 2007; Volume 129, pp. 473–504. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, Y.; Chen, J. Ultrafast solid–liquid–vapor phase change in a thin gold film irradiated by multiple femtosecond laser pulses. Int. J. Heat Mass Transf. 2009, 52, 3091–3100. [Google Scholar] [CrossRef]
- Xu, X.; Chen, G.; Song, K. Experimental and numerical investigation of heat transfer and phase change phenomena during excimer laser interaction with nickel. Int. J. Heat Mass Transf. 1999, 42, 1371–1382. [Google Scholar] [CrossRef]
- Tang, D.; Araki, N. Wavy, wavelike, diffusive thermal responses of finite rigid slabs to high-speed heating of laser-pulses. Int. J. Heat Mass Transf. 1999, 42, 855–860. [Google Scholar] [CrossRef]













| Time [ps] | 0.1 | 0.2 | 0.3 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
|---|---|---|---|---|---|---|---|---|---|
| Experiment | 0.11 | 0.40 | 1.0 | 0.65 | 0.38 | 0.24 | 0.20 | 0.12 | 0.10 |
| Model | 0..11 | 0.38 | 1.0 | 0.67 | 0.36 | 0.22 | 0.19 | 0.11 | 0.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Majchrzak, E.; Mochnacki, B. Sensitivity of a Process for Heating Thin Metal Film Described by the Dual-Phase Lag Equation with Temperature-Dependent Thermophysical Parameters to Perturbations of Lag Times. Energies 2024, 17, 2252. https://doi.org/10.3390/en17102252
Majchrzak E, Mochnacki B. Sensitivity of a Process for Heating Thin Metal Film Described by the Dual-Phase Lag Equation with Temperature-Dependent Thermophysical Parameters to Perturbations of Lag Times. Energies. 2024; 17(10):2252. https://doi.org/10.3390/en17102252
Chicago/Turabian StyleMajchrzak, Ewa, and Bohdan Mochnacki. 2024. "Sensitivity of a Process for Heating Thin Metal Film Described by the Dual-Phase Lag Equation with Temperature-Dependent Thermophysical Parameters to Perturbations of Lag Times" Energies 17, no. 10: 2252. https://doi.org/10.3390/en17102252





