Development of a Homogenized Finite Element Model for Pouch Lithium-Ion Battery Cells Considering Porosity and Pressure Sensitivity
Abstract
:1. Introduction
2. Material Models
3. Finite Element Models and Simulations
3.1. Homogenized J & M Model
3.2. Determination of Material Properties of the J & M Model
3.2.1. First Battery and Second Battery Tested by Sahraei et al.
3.2.2. Third Battery Tested by Beaumont et al.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, J.; Wierzbicki, T.; Li, W. A Review of Safety-Focused Mechanical Modeling of Commercial Lithium-Ion Batteries. J. Power Sources 2018, 378, 153–168. [Google Scholar] [CrossRef]
- ABAQUS 2020 Documentation; Dassault Systemes: France, Paris, 2020.
- Wang, W.; Yang, S.; Lin, C.; Li, Y. State of Charge Dependent Constitutive Model of the Jellyroll of Cylindrical Lithium-Ion Cells. IEEE Access 2018, 6, 26358–26366. [Google Scholar] [CrossRef]
- Sahraei, E.; Hill, R.; Wierzbicki, T. Calibration and Finite Element Simulation of Pouch Lithium-Ion Batteries for Mechanical Integrity. J. Power Sources 2012, 201, 307–321. [Google Scholar] [CrossRef]
- Livermore Software Technology Corporation (LSTC). LS-DYNA Keyword User’s Manual Volume II Material Models LS-DYNA, 11th ed.; LSTC: Livermore, CA, USA, 2018. [Google Scholar]
- Beaumont, R.; Masters, I.; Das, A.; Lucas, S.; Thanikachalam, A.; Williams, D. Methodology for Developing a Macro Finite Element Model of Lithium-Ion Pouch Cells for Predicting Mechanical Behaviour under Multiple Loading Conditions. Energies 2021, 14, 1921. [Google Scholar] [CrossRef]
- Song, Y.; Gilaki, M.; Keshavarzi, M.M.; Sahraei, E. A Universal Anisotropic Model for a Lithium-ion Cylindrical Cell Validated under Axial, Lateral, and Bending Loads. Energy Sci. Eng. 2022, 10, 1431–1448. [Google Scholar] [CrossRef]
- Keshavarzi, M.M.; Gilaki, M.; Sahraei, E. Characterization of In-Situ Material Properties of Pouch Lithium-Ion Batteries in Tension from Three-Point Bending Tests. Int. J. Mech. Sci. 2022, 219, 107090. [Google Scholar] [CrossRef]
- Kermani, G.; Keshavarzi, M.M.; Sahraei, E. Deformation of Lithium-Ion Batteries under Axial Loading: Analytical Model and Representative Volume Element. Energy Rep. 2021, 7, 2849–2861. [Google Scholar] [CrossRef]
- Ali, M.Y.; Lai, W.-J.; Pan, J. Computational Models for Simulations of Lithium-Ion Battery Cells under Constrained Compression Tests. J. Power Sources 2013, 242, 325–340. [Google Scholar] [CrossRef]
- Jeong, H.-Y. A New Yield Function and a Hydrostatic Stress-Controlled Void Nucleation Model for Porous Solids with Pressure-Sensitive Matrices. Int. J. Solids Struct. 2002, 39, 1385–1403. [Google Scholar] [CrossRef]
- Wang, H.; Duan, X.; Liu, B. The Anisotropic Homogenized Model for Pouch Type Lithium-Ion Battery Under Various Abuse Loadings. J. Electrochem. Energy Convers. Storage 2021, 18, 021015. [Google Scholar] [CrossRef]
- Gupta, P.; Gudmundson, P. Modeling of Local Electrode Stresses and Pressures in Lithium-Ion Battery Packs Using Three-Dimensional Homogenization. J. Power Sources 2023, 582, 233514. [Google Scholar] [CrossRef]
- Spitzig, W.A.; Sober, R.J.; Richmond, O. Pressure Dependence of Yielding and Associated Volume Expansion in Tempered Martensite. Acta Metall. 1975, 23, 885–893. [Google Scholar] [CrossRef]
- Spitzig, W.A.; Sober, R.J.; Richmond, O. The Effect of Hydrostatic Pressure on the Deformation Behavior of Maraging and HY-80 Steels and Its Implications for Plasticity Theory. Metall. Trans. A 1976, 7, 1703–1710. [Google Scholar] [CrossRef]
- Kinloch, A.J.; Young, R.J. Fracture Behaviour of Polymers; Springer: Dordrecht, The Netherlands, 2013; ISBN 978-94-017-1594-2. [Google Scholar]
- Gurson, A.L. Plastic Flow and Fracture Behavior of Ductile Materials Incorporating Void Nucleation, Growth and Interaction. Ph.D. Thesis, Brown University, Providence, RI, USA, 1975. [Google Scholar]
- Gurson, A.L. Continuum Theory of Ductile Rupture by Void Nucleation and Growth: Part I—Yield Criteria and Flow Rules for Porous Ductile Media. J. Eng. Mater. Technol. 1977, 99, 2–15. [Google Scholar] [CrossRef]
- Spitzig, W.A.; Richmond, O. Effect of Hydrostatic Pressure on the Deformation Behavior of Polyethylene and Polycarbonate in Tension and in Compression. Polym. Eng. Sci 1979, 19, 1129–1139. [Google Scholar] [CrossRef]
- Tvergaard, V.; Needleman, A. Analysis of the Cup-Cone Fracture in a Round Tensile Bar. Acta Metall. 1984, 32, 157–169. [Google Scholar] [CrossRef]
- Fei, H.; Yazzie, K.; Chawla, N.; Jiang, H. The Effect of Random Voids in the Modified Gurson Model. J. Electron. Mater. 2012, 41, 177–183. [Google Scholar] [CrossRef]
- Ellis, L.D.; Allen, J.P.; Thompson, L.M.; Harlow, J.E.; Stone, W.J.; Hill, I.G.; Dahn, J.R. Quantifying, Understanding and Evaluating the Effects of Gas Consumption in Lithium-Ion Cells. J. Electrochem. Soc. 2017, 164, A3518–A3528. [Google Scholar] [CrossRef]
- Choi, H.Y.; Lee, I.; Lee, J.S.; Kim, Y.M.; Kim, H. A study on mechanical characteristics of lithium-polymer pouch cell battery for electric vehicle. In Proceedings of the 23rd International Technical Conference on the Enhanced Safety of Vehicles (ESV), Seoul, Republic of Korea, 27–30 May 2013. [Google Scholar]
- Lian, J.; Koch, M.; Li, W.; Wierzbicki, T.; Zhu, J. Mechanical Deformation of Lithium-Ion Pouch Cells under in-Plane Loads—Part II: Computational Modeling. J. Electrochem. Soc. 2020, 167, 090556. [Google Scholar] [CrossRef]
- Kisters, T.; Sahraei, E.; Wierzbicki, T. Dynamic Impact Tests on Lithium-Ion Cells. Int. J. Impact Eng. 2017, 108, 205–216. [Google Scholar] [CrossRef]
- Ratner, A.; Beaumont, R.; Masters, I. Dynamic Mechanical Compression Impulse of Lithium-Ion Pouch Cells. Energies 2020, 13, 2105. [Google Scholar] [CrossRef]
- Kisters, T.; Gilaki, M.; Nau, S.; Sahraei, E. Modeling of Dynamic Mechanical Response of Li-Ion Cells with Homogenized Electrolyte-Solid Interactions. J. Energy Storage 2022, 49, 104069. [Google Scholar] [CrossRef]
- Li, W.; Zhu, J. A Large Deformation and Fracture Model of Lithium-Ion Battery Cells Treated as a Homogenized Medium. J. Electrochem. Soc. 2020, 167, 120504. [Google Scholar] [CrossRef]

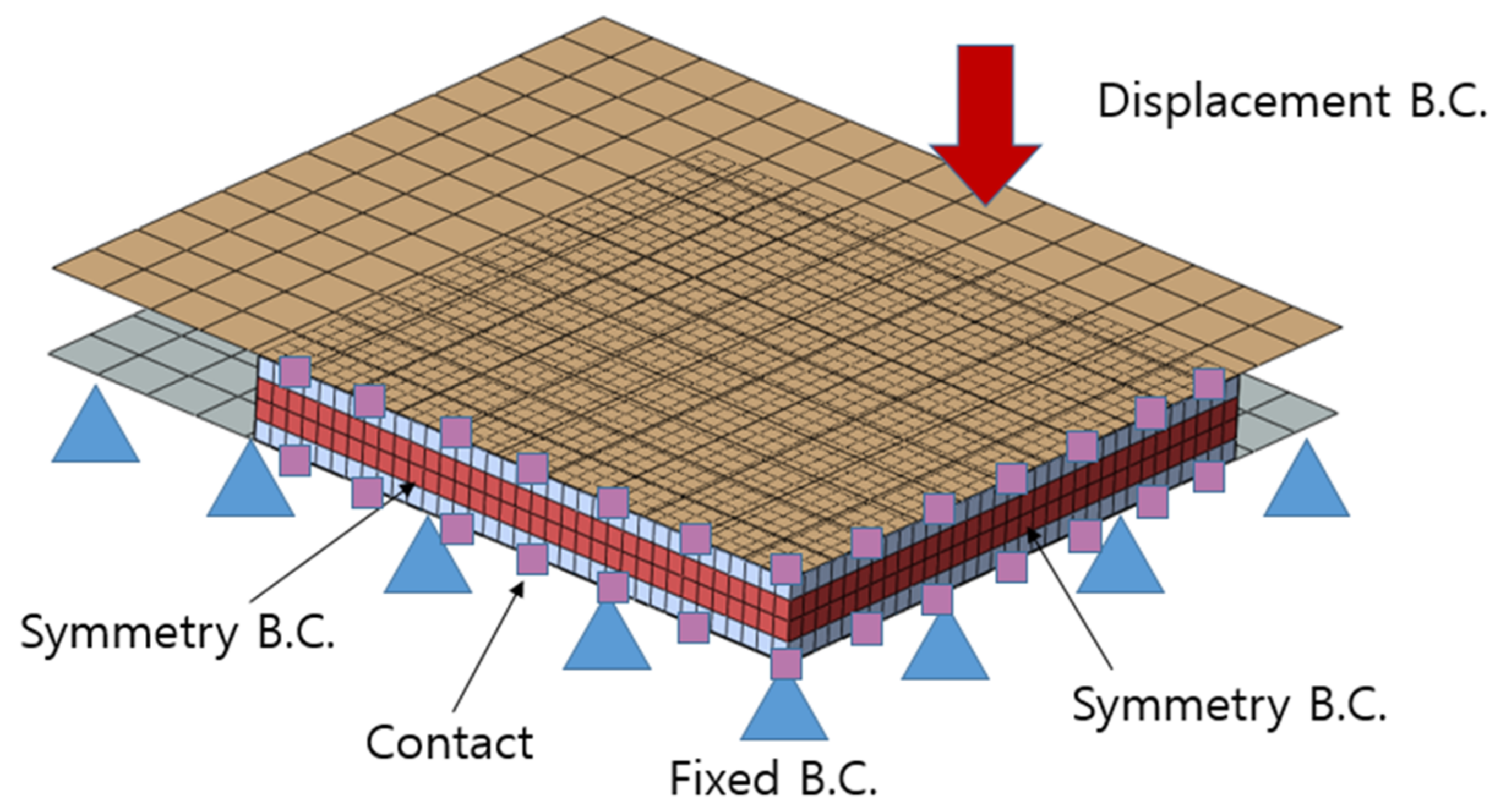









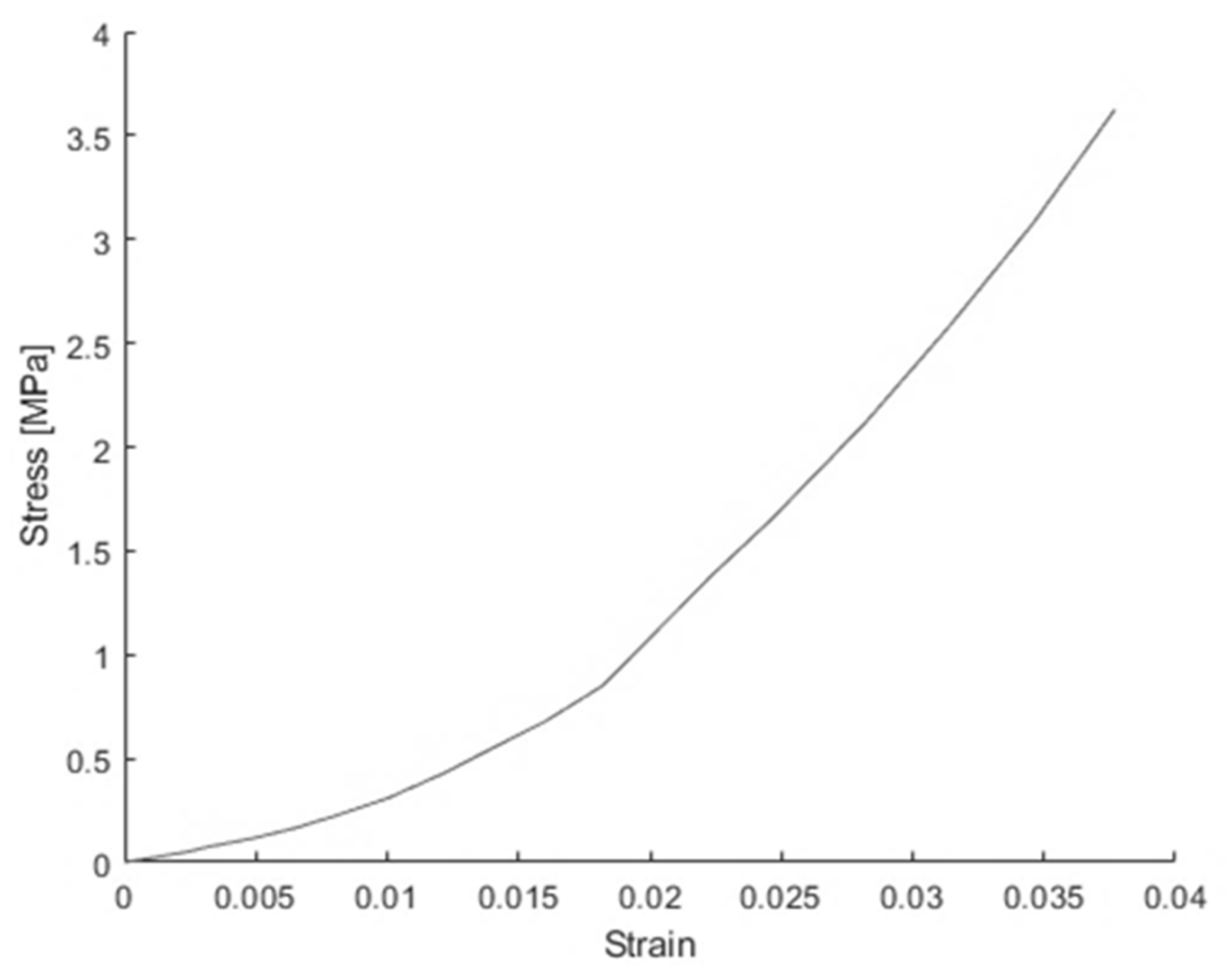








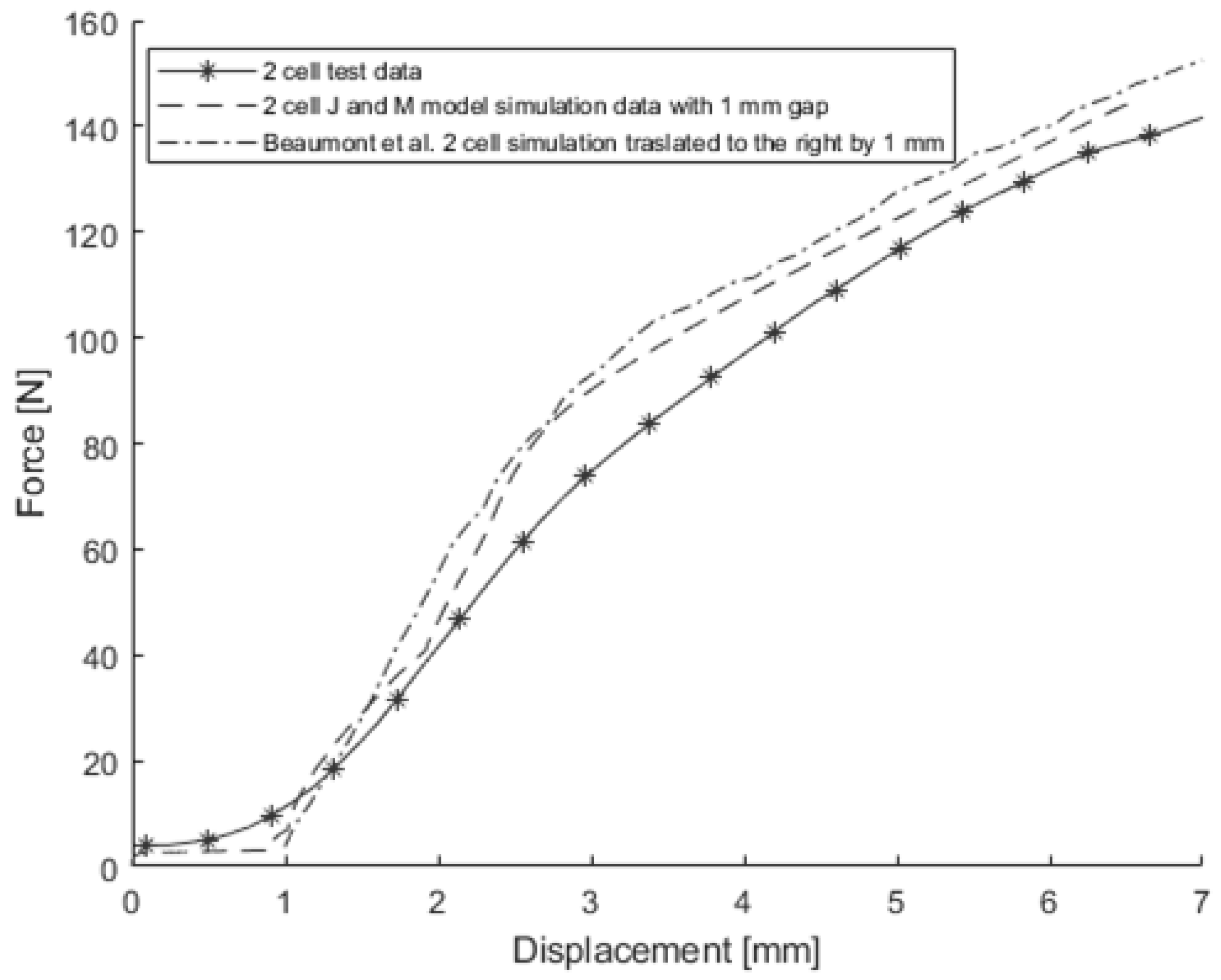




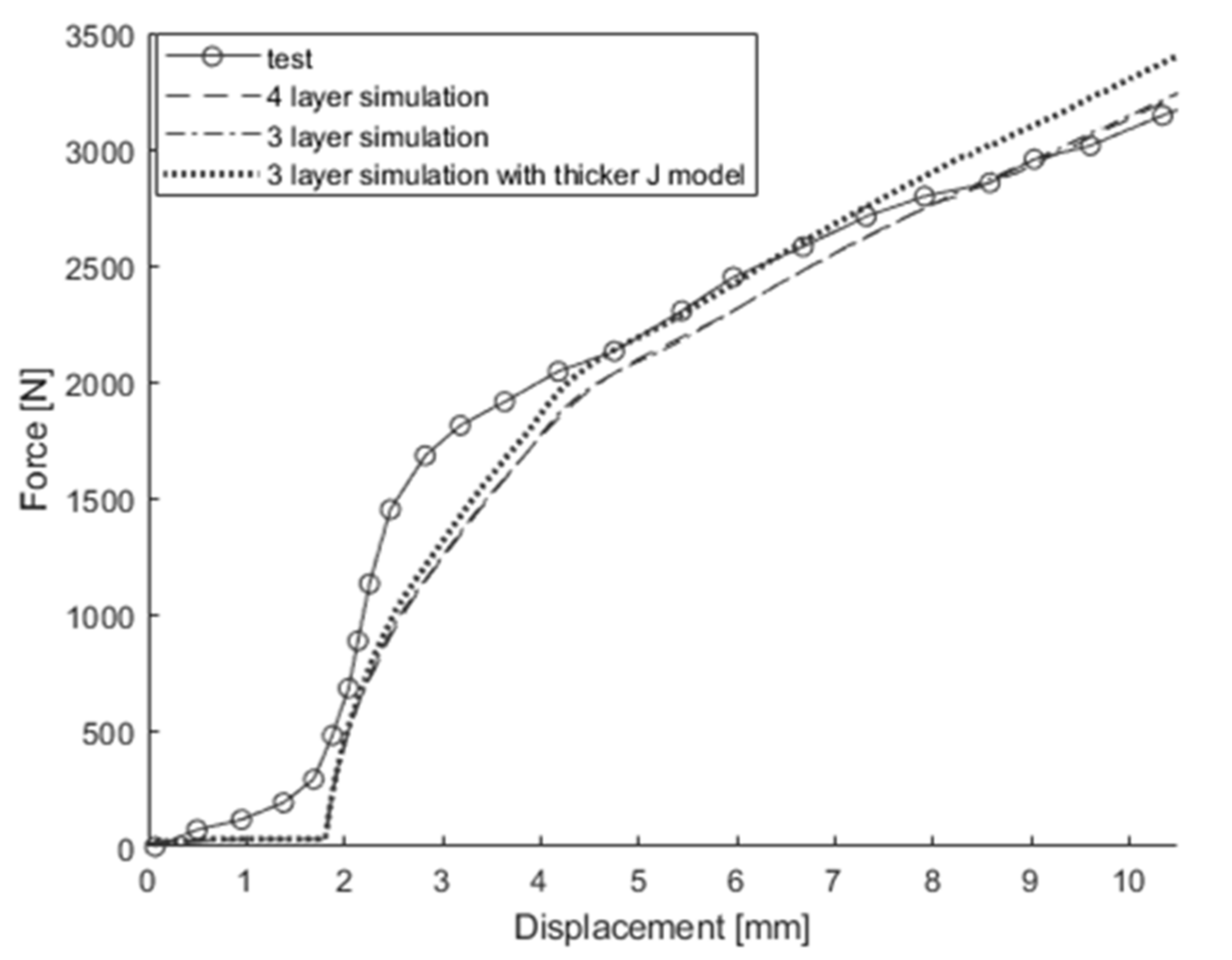


| First and Second Battery | |
|---|---|
| Test Case | J & M Simulation Error [%] |
| Out-of-plane compression | 11.69 |
| Out-of-plane compression w/o vacuum | 16.00 |
| Out-of-plane compression w/o the pouch | 0.23 |
| 3-point bending around the length direction w/o the pouch | 28.95 |
| 3-point bending around the length direction with the pouch | 13.93 |
| 3-point bending around the length direction w/o vacuum | 19.86 |
| Third Battery | |||
|---|---|---|---|
| Test Case | Number of Cells | Beaumont et al.’s Simul. Error [%] | J & M Simulation Error [%] |
| Out-of-plane compression | Single cell | 0 | 4.42 |
| Two stacked cells | 6.04 | 12.55 | |
| Confined in-plane compression in the length direction | Single cell | 6.30 | 16.97 |
| Two stacked cells | 27.00 | 8.40 | |
| Confined in-plane compression in the width direction | Single cell | 3.12 | 19.04 |
| Two stacked cells | 29.97 | 2.17 | |
| 3-point bending around the length direction | Single cell | 3.48 | 14.96 |
| Two stacked cells | 20.41 | 15.86 | |
| 3-point bending around the width direction | Single cell | 3.07 | 16.06 |
| Two stacked cells | 35.05 | 31.96 | |
| Battery | Battery Model | Test | Model Type | Number of Elements | |
|---|---|---|---|---|---|
| Solid | Shell | ||||
| First battery | Sahraei’s detailed model | Out-of-plane compression | Full model | 30,000 | 31,500 |
| J & M model | Quarter model | 880 | 564 | ||
| Second battery | J & M model | 3-point bending | Quarter model | 1408 | 876 |
| Third battery | Beaumont et al.’s homogenized model | 3-point bending, out-of-plane compression | Full model | 3060 | 2424 |
| J & M model with fine elements | Quarter model | 4620 | 2582 | ||
| J & M model with coarse elements | Quarter model | 1224 | 682 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, H.-Y.; Park, J. Development of a Homogenized Finite Element Model for Pouch Lithium-Ion Battery Cells Considering Porosity and Pressure Sensitivity. Energies 2024, 17, 1162. https://doi.org/10.3390/en17051162
Jeong H-Y, Park J. Development of a Homogenized Finite Element Model for Pouch Lithium-Ion Battery Cells Considering Porosity and Pressure Sensitivity. Energies. 2024; 17(5):1162. https://doi.org/10.3390/en17051162
Chicago/Turabian StyleJeong, Hyun-Yong, and Jinwoo Park. 2024. "Development of a Homogenized Finite Element Model for Pouch Lithium-Ion Battery Cells Considering Porosity and Pressure Sensitivity" Energies 17, no. 5: 1162. https://doi.org/10.3390/en17051162




