Research on Multi-Objective Optimization of Renovation Projects in Old Residential Areas Based on Evolutionary Algorithms
Abstract
:1. Introduction
2. Models and Methods
2.1. Construction Phase Multi-Objective Model Construction
2.1.1. Multi-Objective Factor Analysis
2.1.2. Mathematical model establishment
- (I)
- Objective function
- (II)
- Constraint condition
2.2. Solving Multi-Objective Optimization Problems Based on the Evolutionary Algorithm
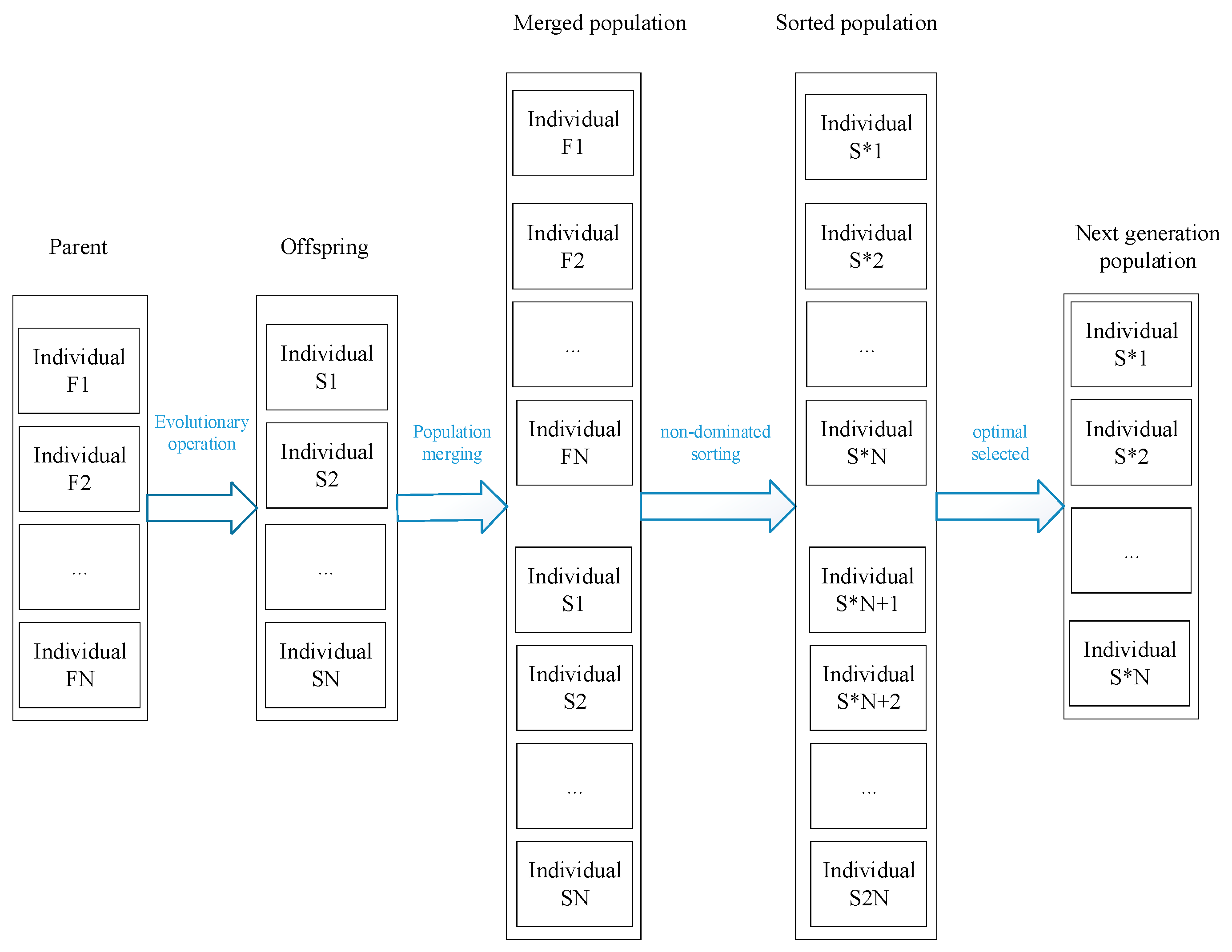
2.2.1. Application of the NSGA-II Algorithm
- (I)
- Parameter settings: Set the population size to N, the number of iterations to M, and the crossover probability and mutation probability to Pc and Pm, respectively.
- (II)
- Population initialization: Generate the initial population based on the coding scheme and assign initial gene values.
- (III)
- Fitness evaluation: First, the duration, cost, and quality target values for each individual in the current population are calculated. Then, non-dominated sorting is performed on the population’s individuals to form different levels, and the crowding distance is calculated for individuals at the same level. Finally, all individuals in the population are sorted.
- (IV)
- Perform evolutionary operations: Perform selection, crossover, and mutation operations on contemporary population F to generate a new population S.
- (V)
- Elitism reserved strategy: Mix the parent population F and the offspring population S, and reallocate the fitness. Individuals with larger crowding distances are selected from lower levels to enter the next-generation population, forming a new population S* with a size of N.
- (VI)
- Termination judgment: Return to step four and continue to the next iteration. Cease the operation once the maximum number of iterations has been reached, and produce the optimal solution.
2.2.2. Algorithm Encoding and Initialization
2.2.3. Virtual Fitness Allocation
- (I)
- Non-dominated sorting
- (II)
- Crowding distance
2.2.4. Evolutionary Operation
- (I)
- Selection
- (II)
- Crossover
- (III)
- Mutation
- (IV)
- Elite preservation strategies
3. Case Analysis
3.1. Project Overview
3.2. Model Application
4. Results and Discussion
4.1. Model Solution
4.2. Multi-Objective Decision Making
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, Y.; Mo, D.; Tang, S.; Li, H. Measuring real estate policy uncertainty in China. China Econ. Q. Int. 2023, 3, 23–34. [Google Scholar] [CrossRef]
- Zhang, H.; Li, L.; Chen, T.; Li, V. Where will China’s real estate market go under the economy’s new normal? Cities 2016, 55, 42–48. [Google Scholar] [CrossRef]
- Ding, Q.; Zhang, T.; Zhu, X.; Zhang, J. Impact of Perceived Value and Community Attachment on Smart Renovation Participation Willingness for Sustainable Development of Old Urban Communities in China. Sustainability 2022, 14, 11675. [Google Scholar] [CrossRef]
- Lihtmaa, L.; Kalamees, T. Emerging renovation strategies and technical solutions for mass-construction of residential districts built after World War II in Europe. Energy Strategy Rev. 2024, 51, 101282. [Google Scholar] [CrossRef]
- Shach-Pinsly, D. Three Strategies of Urban Renewal for One National Outline Plan TAMA38: The Impact of Multiparametric Decision-Making on Neighborhood Regeneration. Architecture 2022, 2, 616–636. [Google Scholar] [CrossRef]
- Shen, T.; Yao, X.; Wen, F. The Urban Regeneration Engine Model: An analytical framework and case study of the renewal of old communities. Land Use Policy 2021, 108, 105571. [Google Scholar] [CrossRef]
- Lekan, A.; Faith, O.; Cinwosoko Ninma, A.; Oladipupo Sunday, A. Data on System Approach to Process of urban housing construction, renewal and upgrading. Data Brief. 2018, 19, 2427–2437. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Lan, F.; Zhou, T. An experience-based mining approach to supporting urban renewal mode decisions under a multi-stakeholder environment in China. Land Use Policy 2021, 106, 105428. [Google Scholar] [CrossRef]
- Zhu, S.; Li, D.; Feng, H.; Gu, T.; Zhu, J. AHP-TOPSIS-based evaluation of the relative performance of multiple neighborhood renewal projects: A case study in Nanjing, China. Sustainability 2019, 11, 4545. [Google Scholar] [CrossRef]
- Huo, X.; Xue, H.; Jiao, L. Risk management of retrofit project in old residential areas under green development. Energy Build. 2023, 279, 112708. [Google Scholar] [CrossRef]
- Luo, X.; Ren, M.; Zhao, J.; Wang, Z.; Ge, J.; Gao, W. Life cycle assessment for carbon emission impact analysis for the renovation of old residential areas. J. Clean. Prod. 2022, 367, 132930. [Google Scholar] [CrossRef]
- He, Y.; Wang, Y.; Song, Z.; Yu, H.; Xue, Y. Study on Carbon Emissions from the Renovation of Old Residential Areas in Cold Regions of China. Sustainability 2023, 15, 3018. [Google Scholar] [CrossRef]
- Feng, H.; Liyanage, D.R.; Karunathilake, H.; Sadiq, R.; Hewage, K. BIM-based life cycle environmental performance assessment of single-family houses: Renovation and reconstruction strategies for aging building stock in British Columbia. J. Clean. Prod. 2020, 250, 119543. [Google Scholar] [CrossRef]
- Ning, X.; Qi, J.; Wu, C.; Wang, W. Reducing noise pollution by planning construction site layout via a multi-objective optimization model. J. Clean. Prod. 2019, 222, 218–230. [Google Scholar] [CrossRef]
- Anvari, B.; Angeloudis, P.; Ochieng, W.Y. A multi-objective GA-based optimisation for holistic Manufacturing, transportation and Assembly of precast construction. Autom. Constr. 2016, 71, 226–241. [Google Scholar] [CrossRef]
- Tran, D.H.; Cheng, M.Y.; Prayogo, D. A novel Multiple Objective Symbiotic Organisms Search (MOSOS) for time-cost-labor utilization tradeoff problem. Knowl. Based Syst. 2016, 94, 132–145. [Google Scholar] [CrossRef]
- Li, Z.; Zou, Y.; Xia, H.; Jin, C. Multi-objective optimization design of residential area based on microenvironment simulation. J. Clean. Prod. 2023, 425, 138922. [Google Scholar] [CrossRef]
- Jun, D.H.; El-Rayes, K. Optimizing the utilization of multiple labor shifts in construction projects. Autom. Constr. 2010, 19, 109–119. [Google Scholar] [CrossRef]
- Alsayegh, H.; Hariga, M. Hybrid meta-heuristic methods for the multi-resource leveling problem with activity splitting. Autom. Constr. 2012, 27, 89–98. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Tran, D.H.; Wu, Y.W. Using a fuzzy clustering chaotic-based differential evolution with serial method to solve resource-constrained project scheduling problems. Autom. Constr. 2014, 37, 88–97. [Google Scholar] [CrossRef]
- Tran, H.-H.; Hoang, N.-D. A Novel Resource-Leveling Approach for Construction Project Based on Differential Evolution. J. Constr. Eng. 2014, 2014, 1–7. [Google Scholar] [CrossRef]
- Chen, P.H.; Weng, H. A two-phase GA model for resource-constrained project scheduling. Autom. Constr. 2009, 18, 485–498. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, C. Research on multi-objective optimization of construction engineering based on improved genetic algorithm. Procedia Comput. Sci. 2023, 228, 1086–1091. [Google Scholar] [CrossRef]
- Immanuel, S.D.; Chakraborty, U.K. Genetic Algorithm: An Approach on Optimization. In Proceedings of the International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 17–19 July 2019; pp. 701–708. [Google Scholar]
- Gang, L. Genetic Algorithm and Its Application in Software Test Data Generation. In Proceedings of the International Conference on Applied Intelligence and Sustainable Computing (ICAISC), Dharwad, India, 16–17 June 2023. [Google Scholar]
- Shadravan, S.; Naji, H.R.; Bardsiri, V.K. The Sailfish Optimizer: A novel nature-inspired metaheuristic algorithm for solving constrained engineering optimization problems. Eng. Appl. Artif. Intell. 2019, 80, 20–34. [Google Scholar] [CrossRef]
- Shami, T.M.; El-Saleh, A.A.; Alswaitti, M.; Al-Tashi, Q.; Summakieh, M.A.; Mirjalili, S. Particle Swarm Optimization: A Comprehensive Survey. IEEE Access 2022, 10, 10031–10061. [Google Scholar] [CrossRef]
- Gharehchopogh, F.S.; Gholizadeh, H. A comprehensive survey: Whale Optimization Algorithm and its applications. Swarm Evol. Comput. 2019, 48, 1–24. [Google Scholar] [CrossRef]
- Alothaimeen, I.; Arditi, D.; Türkakın, O.H. Multi-objective optimization for LEED—New construction using BIM and genetic algorithms. Autom. Constr. 2023, 149, 104807. [Google Scholar] [CrossRef]
- Wu, X.; Wang, L.; Chen, B.; Feng, Z.; Qin, Y.; Liu, Q.; Liu, Y. Multi-objective optimization of shield construction parameters based on random forests and NSGA-II. Adv. Eng. Inform. 2022, 54, 101751. [Google Scholar] [CrossRef]
- Ghoddousi, P.; Eshtehardian, E.; Jooybanpour, S.; Javanmardi, A. Multi-mode resource-constrained discrete time-cost-resource optimization in project scheduling using non-dominated sorting genetic algorithm. Autom. Constr. 2013, 30, 216–227. [Google Scholar] [CrossRef]






| Work Code | Prior Work | Work Name | Minimum Working Period (Days) | Normal Construction Period (Days) | Longest Construction Period (Days) | Normal Cost (CNY Ten Thousand) | Maximum Cost (CNY Ten Thousand) | Boundary Cost Coefficient | Minimum Quality Requirements |
|---|---|---|---|---|---|---|---|---|---|
| A | \ | Construction of external wall insulation layer | 26 | 28 | 30 | 189 | 192 | 0.06 | 0.90 |
| B | \ | Demolition of external air conditioning units and illegal constructions | 20 | 23 | 26 | 34 | 38 | 0.08 | 0.86 |
| C | A,B | Construction of exterior wall coatings | 6 | 8 | 9 | 82 | 89 | 0.42 | 0.85 |
| D | C | Add security and fire protection facilities | 3 | 4 | 5 | 36 | 39 | 0.34 | 0.83 |
| E | C | Pipeline laying | 10 | 12 | 14 | 200 | 206 | 0.26 | 0.87 |
| F | C | Installation of air conditioning louvers | 7 | 10 | 12 | 23 | 27 | 0.21 | 0.85 |
| G | C | Roof renovation | 25 | 29 | 32 | 66 | 76 | 0.16 | 0.90 |
| H | D,E,F | Road rebuilding | 5 | 8 | 10 | 105 | 110 | 0.33 | 0.85 |
| I | H | Outdoor lighting and landscape construction | 27 | 30 | 34 | 120 | 125 | 0.06 | 0.86 |
| J | I,G | Renovation of parking spaces and addition of car sheds | 3 | 4 | 7 | 9 | 13 | 0.44 | 0.85 |
| K | J | Renovation of building fire exits | 11 | 14 | 15 | 84 | 89 | 0.17 | 0.87 |
| L | K | Restoration and demobilization of construction sites | 2 | 3 | 4 | 18 | 21 | 0.42 | 0.86 |
| Work Code | Prior Work | Work Name | Minimum Working Period (Days) | Longest Construction Period (Days) | Minimum Working Period Total Time Difference (Days) | Longest Construction Period Total Time Difference (Days) |
|---|---|---|---|---|---|---|
| A | \ | Construction of external wall insulation layer | 26 | 30 | 0 | 0 |
| B | \ | Demolition of external air conditioning units and illegal constructions | 20 | 26 | 6 | 4 |
| B1 | B | Virtual work 1 | 0 | 0 | 6 | 4 |
| C | A,B | Construction of exterior wall coatings | 6 | 9 | 0 | 0 |
| D | C | Add security and fire protection facilities | 3 | 5 | 7 | 9 |
| D1 | D | Virtual work 2 | 0 | 0 | 7 | 9 |
| E | C | Pipeline laying | 10 | 14 | 0 | 0 |
| F | C | Installation of air conditioning louvers | 7 | 12 | 3 | 2 |
| F1 | F | Virtual work 3 | 0 | 0 | 3 | 2 |
| G | C | Roof renovation | 25 | 32 | 17 | 26 |
| G1 | G | Virtual work 4 | 0 | 0 | 17 | 26 |
| H | D,E,F | Road rebuilding | 5 | 10 | 0 | 0 |
| I | H | Outdoor lighting and landscape construction | 27 | 34 | 0 | 0 |
| J | I,G | Renovation of parking spaces and addition of car sheds | 3 | 7 | 0 | 0 |
| K | J | Renovation of building fire exits | 11 | 15 | 0 | 0 |
| L | K | Restoration and demobilization of construction sites | 2 | 4 | 0 | 0 |
| Construction Plan | Construction Period (Days) | Cost (CNY Ten Thousand) | Quality Level |
|---|---|---|---|
| 1 | 104 | 1067.38 | 0.84 |
| 2 | 123 | 1036.45 | 0.91 |
| 3 | 112 | 1054.35 | 0.81 |
| 4 | 95 | 1082.66 | 0.82 |
| 5 | 103 | 1070.83 | 0.83 |
| 6 | 101 | 1072.76 | 0.86 |
| 7 | 103 | 1069.42 | 0.79 |
| 8 | 92 | 1087.67 | 0.83 |
| 9 | 123 | 1037.35 | 0.91 |
| 10 | 108 | 1061.02 | 0.82 |
| 11 | 97 | 1079.31 | 0.95 |
| 12 | 90 | 1090.51 | 0.82 |
| 13 | 122 | 1039.23 | 0.85 |
| 14 | 99 | 1076.05 | 0.89 |
| 15 | 115 | 1049.33 | 0.86 |
| 16 | 95 | 1084.65 | 0.92 |
| 17 | 101 | 1074.72 | 0.91 |
| 18 | 90 | 1091.26 | 0.84 |
| Work Code | Duration (Days) | Target Quality | Target Cost (CNY Ten Thousand) | Multi-Objective Optimization Results |
|---|---|---|---|---|
| A | 28 | 0.97 | 209.14 | T = 97 C = 1079.31 Q = 0.95 |
| B | 22 | 0.93 | 51.67 | |
| C | 7 | 0.91 | 87.86 | |
| D | 3 | 0.94 | 37.92 | |
| E | 9 | 0.95 | 30.12 | |
| F | 10 | 0.94 | 206.37 | |
| G | 28 | 0.96 | 87.67 | |
| H | 6 | 0.93 | 110.43 | |
| I | 28 | 0.92 | 141.89 | |
| J | 3 | 0.93 | 11.01 | |
| K | 12 | 0.93 | 85.21 | |
| L | 3 | 0.96 | 20.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Shen, C.; Tang, C.; Feng, L.; Chen, Y.; Yang, S.; Ren, Z. Research on Multi-Objective Optimization of Renovation Projects in Old Residential Areas Based on Evolutionary Algorithms. Buildings 2024, 14, 1485. https://doi.org/10.3390/buildings14051485
Zhang J, Shen C, Tang C, Feng L, Chen Y, Yang S, Ren Z. Research on Multi-Objective Optimization of Renovation Projects in Old Residential Areas Based on Evolutionary Algorithms. Buildings. 2024; 14(5):1485. https://doi.org/10.3390/buildings14051485
Chicago/Turabian StyleZhang, Jiaji, Chuxiong Shen, Chao Tang, Liang Feng, Yuliang Chen, Shize Yang, and Zhigang Ren. 2024. "Research on Multi-Objective Optimization of Renovation Projects in Old Residential Areas Based on Evolutionary Algorithms" Buildings 14, no. 5: 1485. https://doi.org/10.3390/buildings14051485





