Analyzing the Impact of Geometrophysical Modeling on Highway Design Speeds: A Comparative Study for Mexico’s Case
Abstract
:1. Introduction and Antecedents
2. A Brief Comment on Geometrophysical Modeling
2.1. Fundamental Principles
2.2. Modeling Dynamics
2.3. Application to Highway Regulations
2.4. Comparative Analysis
2.5. Relevance of Geometrophysical Modeling/Examples
3. Analytical Model Conceptual Development and Discussion
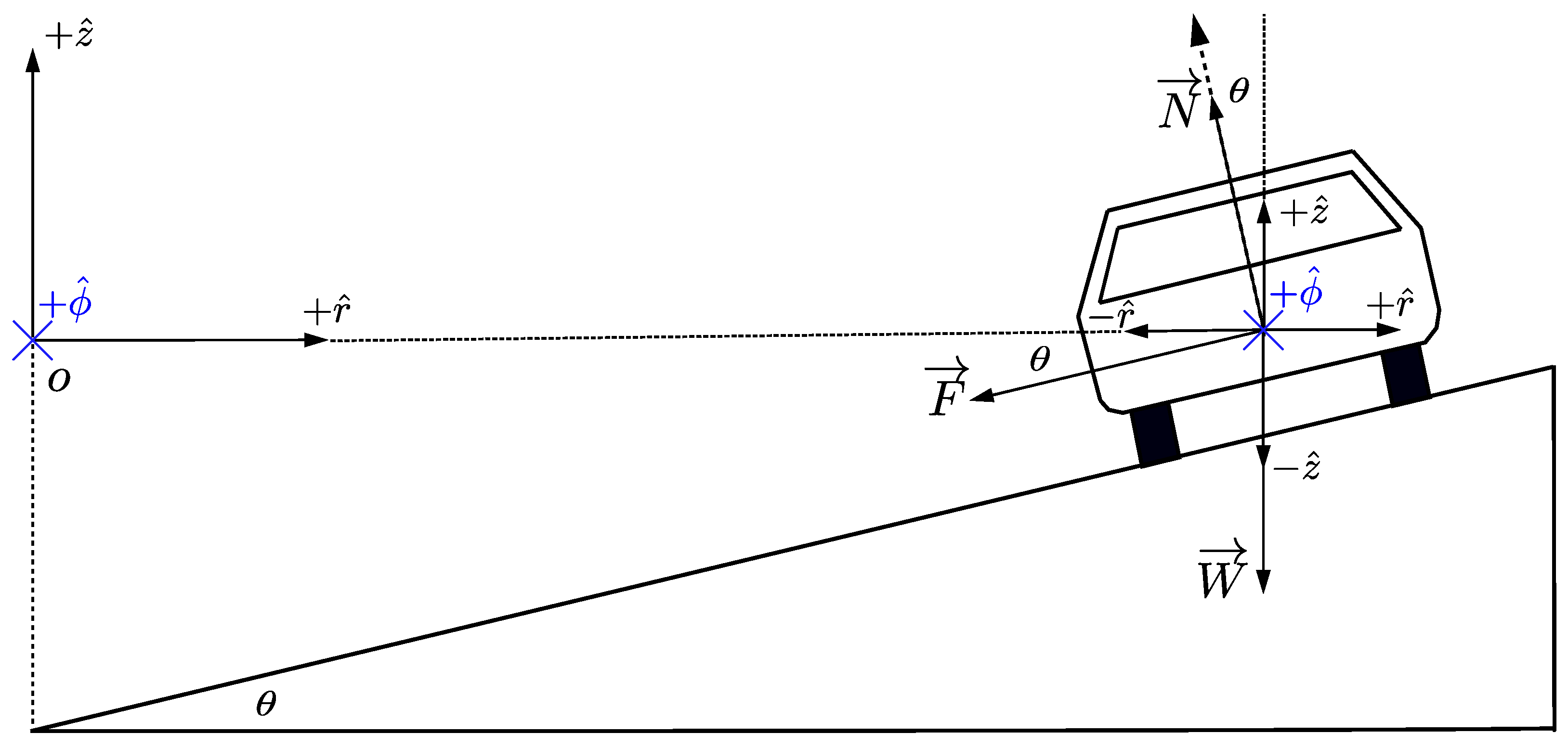
3.1. Instantaneous Radius of Curvature Model (IRCM) for Highway Vehicle Dynamics: Normal and Tangential Coordinates


- (i)
- A 2D model is used to ascertain a 3D situation. The motion of a vehicle on the highway can not be reduced to normal and tangential components. For the model to make sense, another coordinate along is used.
- (ii)
- A radius of the curvature (R) notion only makes sense when considering sequences of precise segments of circular/curvilinear sections; that is, definite arc segments of the vehicle’s trajectory, as shown in Figure 3.
- (iii)
3.2. Highway Vehicle Dynamics Studied by Cylindrical-Polar Coordinates: Plane of Vehicle Motion Rotated with Respect to Horizontal Plane
3.3. Highway Vehicle Dynamics Studied by Cylindrical-Polar Coordinates: Plane of Motion Unrotated with Respect to the Horizontal Plane (i.e., Parallel to It)
3.4. Highway Vehicle Dynamics Studied by Spherical Coordinates
4. Results Comparative Presentation and Discussion
5. Parametric Sweep: Visualization and Analysis
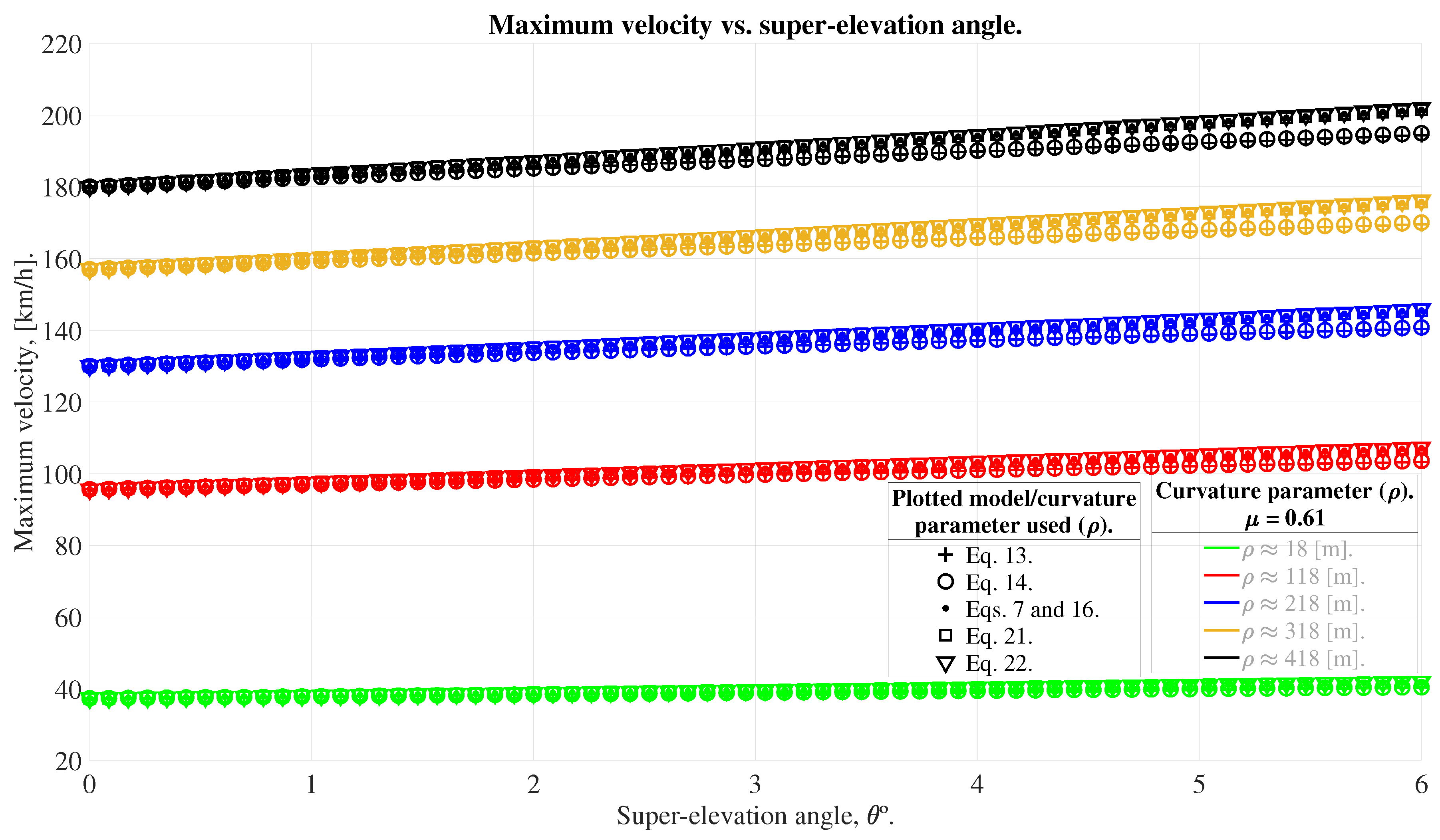
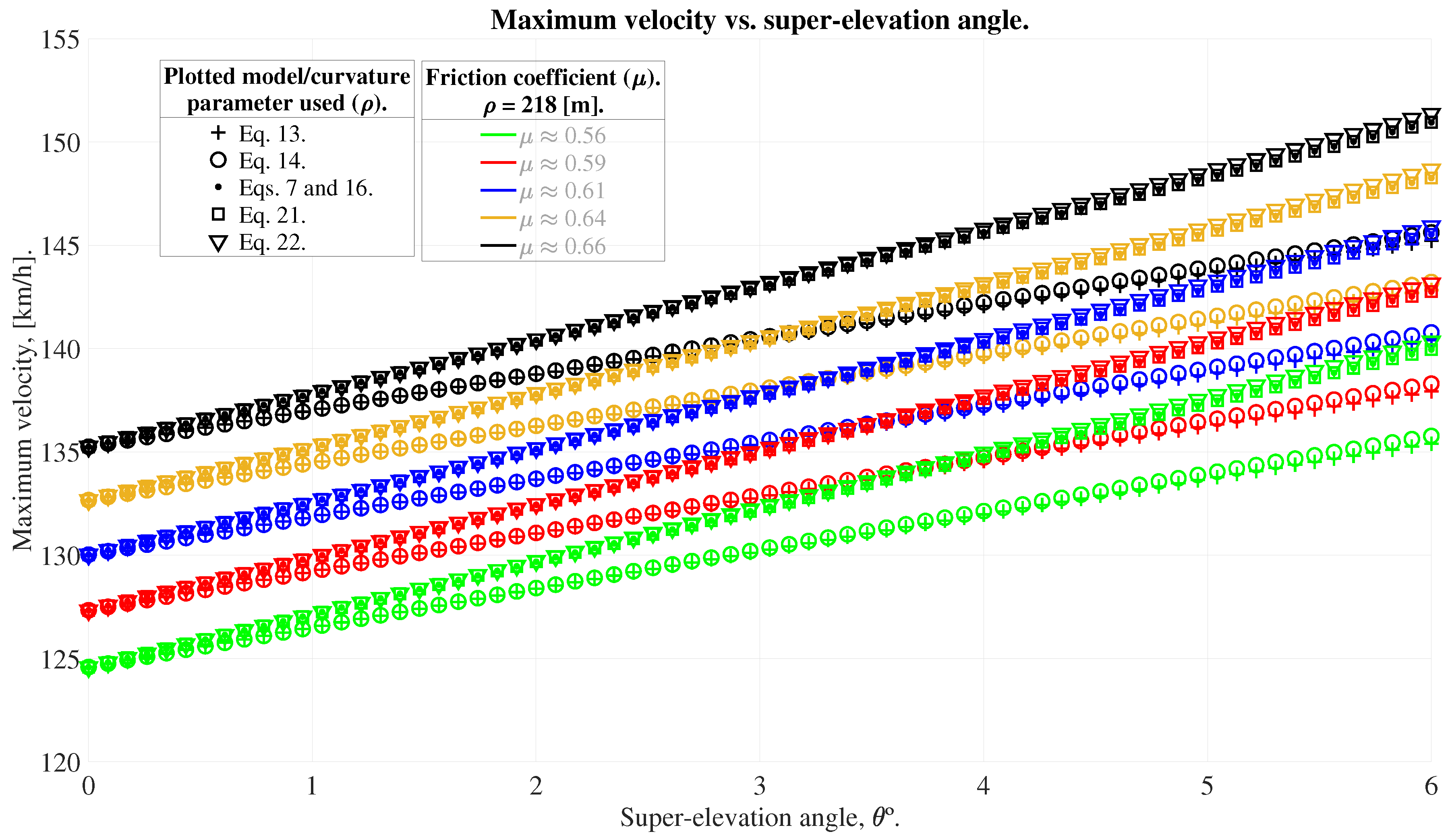

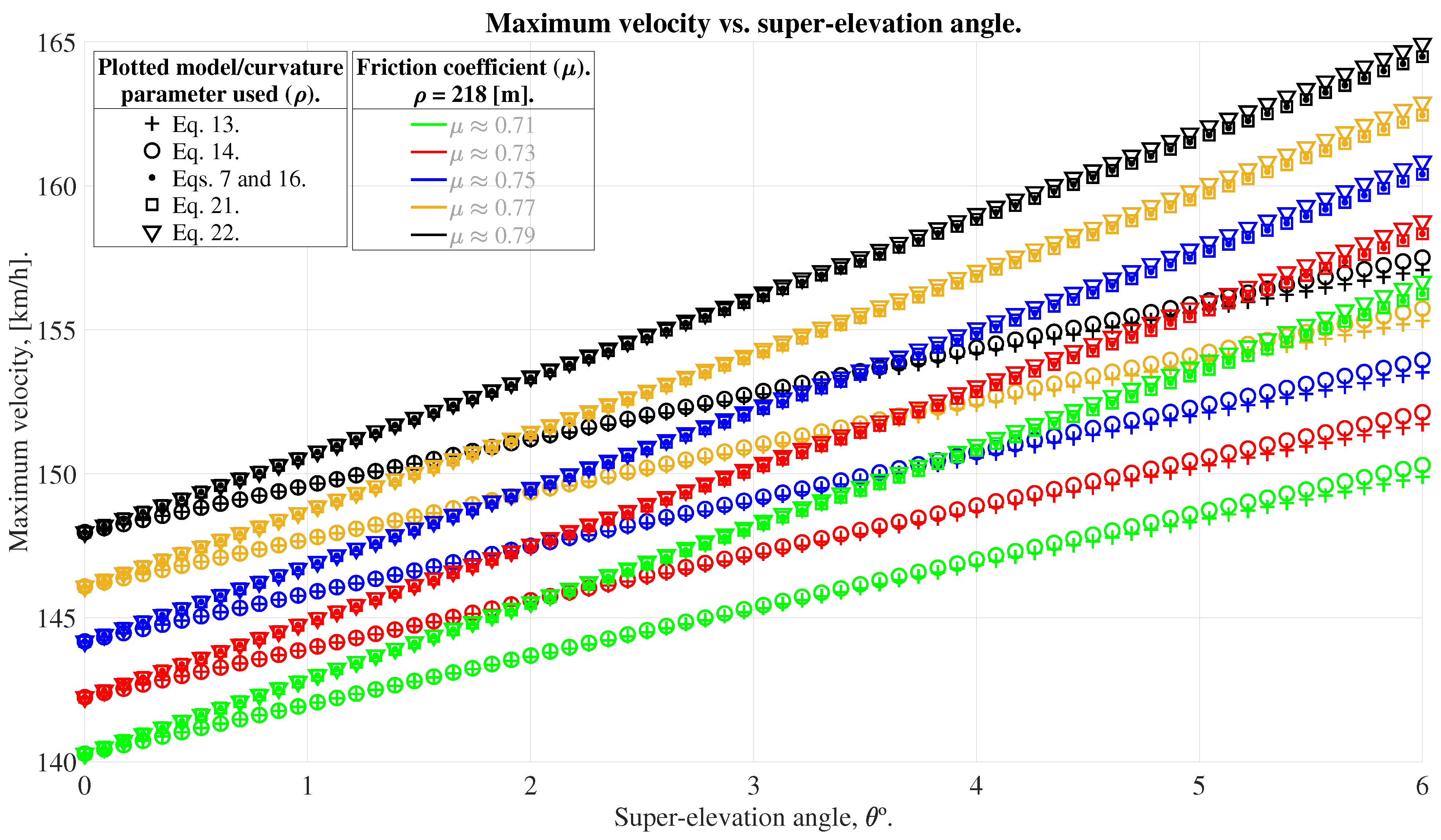


6. Observations/Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, Y.; Mi, J.; Yang, X.; Sun, Z.; Liu, C. Prediction model and sensitivity analysis of ultimate drift ratio for rectangular reinforced concrete columns failed in flexural-shear based on BP-Garson algorithm. Structures 2024, 60, 105808. [Google Scholar] [CrossRef]
- Liu, C.; Zhao, B.; Yang, J.; Yi, Q.; Yao, Z.; Wu, J. Effects of brace-to-chord angle on capacity of multi-planar CHS X-joints under out-of-plane bending moments. Eng. Struct. 2020, 211, 110434. [Google Scholar] [CrossRef]
- Montella, A.; Galante, F.; Mauriello, F.; Aria, M. Continuous speed profiles to investigate drivers’ behavior on two-lane rural highways. Transp. Res. Rec. 2015, 2521, 3–11. [Google Scholar] [CrossRef]
- Choi, J.; Tay, R.; Kim, S. Effects of changing highway design speed. J. Adv. Transp. 2013, 47, 239–246. [Google Scholar] [CrossRef]
- Shaon, M.R.R.; Qin, X.; Chen, Z.; Zhang, J. Exploration of contributing factors related to driver errors on highway segments. Transp. Res. Rec. 2018, 2672, 22–34. [Google Scholar] [CrossRef]
- Fitzpatrick, K.; Zimmerman, K. Potential updates to 2004 green book’s acceleration lengths for entrance terminals. Transp. Res. Rec. 2007, 2023, 130–139. [Google Scholar] [CrossRef]
- Figueroa-Medina, A.; Tarko, A. Reconciling speed limits with design speeds. Jt. Transp. Res. Program 2004, FHWA/IN/JTRP-2004/26. [Google Scholar]
- Fu, M. Research on Superelevation Design in Highway Route Design. J. World Archit. 2021, 5. [Google Scholar] [CrossRef]
- Abdulhafedh, A. Design of superelevation of highway curves: An overview and distribution methods. J. City Dev. 2019, 1, 35–40. [Google Scholar]
- Craus, J.; Livneh, M. Superelevation and curvature of horizontal curves. Transp. Res. Rec. 1978, 685, 7–13. [Google Scholar]
- Himes, S.; Porter, R.; Hamilton, I.; Eric, D. Safety evaluation of geometric design criteria: Horizontal curve radius and side friction demand on rural, two-lane highways. Transp. Res. Rec. 2019, 2673, 516–525. [Google Scholar] [CrossRef]
- Jiang, F.; Sun, X.; Li, H.; Huang, J.; Li, D. Optimization Analysis of Minimum Flat Curve Radius of High Speed Maglev Line with Design Speed of 500 km/h. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Sabah, Malaysia, 9–11 August 2019; Volume 637, pp. 012008–012015. [Google Scholar]
- Nazmul, H. Maximum allowable speed on curve. In Proceedings of the ASME/IEEE Joint Rail Conference, Pueblo, CO, USA, 16–18 March 2011; Volume 54594, pp. 1–9. [Google Scholar]
- Richl, L.; Sayed, T. Effect of speed prediction models and perceived radius on design consistency. Can. J. Civ. Eng. 2005, 32, 388–399. [Google Scholar] [CrossRef]
- Schurr, K.; McCoy, P.; Pesti, G.; Huff, R. Relationship of design, operating, and posted speeds on horizontal curves of rural two-lane highways in Nebraska. Transp. Res. Rec. 2002, 1796, 60–71. [Google Scholar] [CrossRef]
- Miaou, S.P.; Lum, H. Modeling vehicle accidents and highway geometric design relationships. Accid. Anal. Prev. 1993, 25, 689–709. [Google Scholar] [CrossRef] [PubMed]
- Vayalamkuzhi, P.; Amirthalingam, V. Influence of geometric design characteristics on safety under heterogeneous traffic flow. J. Traffic Transp. Eng. 2016, 3, 559–570. [Google Scholar] [CrossRef]
- Ruiz, G.; Callejo, O.; Verdugo, J. Manual de proyecto geométrico de carreteras 2018. 2018. Available online: http://sct.gob.mx/normatecaNew/manual-de-proyecto-geometrico-de-carreteras/ (accessed on 6 May 2024).
- Albattah, M. Optimum highway design and site location using spatial geoinformatics engineering. J. Remote Sens. GIS 2016, 5, 10. [Google Scholar]
- Boas, P.R.V.; Rodrigues, F.A.; Costa, L.d.F. Modeling worldwide highway networks. Phys. Lett. A 2009, 374, 22–27. [Google Scholar] [CrossRef]
- Biancardo, S.A.; Capano, A.; de Oliveira, S.G.; Tibaut, A. Integration of BIM and procedural modeling tools for road design. Infrastructures 2020, 5, 37. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W.; Liu, J.; Chen, T.; Wang, S.; Yu, B.; Qin, X. Framework for geometric information extraction and digital modeling from LiDAR data of road scenarios. Remote Sens. 2023, 15, 576. [Google Scholar] [CrossRef]
- Qi, H.; Cong, B.; Liu, R.; Li, X.; Yan, Z.; Li, Q.; Li, M. Research on the 3D fine modeling method of In-service road. Adv. Civ. Eng. 2023, 2023, 7336379. [Google Scholar] [CrossRef]
- Wei, Y.; Zhang, Z.; Huang, X.; Lin, Y.; Liu, W. 3D highway curve reconstruction from mobile laser scanning point clouds through deep reinforcement learning. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, 48, 55–61. [Google Scholar] [CrossRef]
- AASHTO. A Policy on Geometric Design of Highways and Streets; AASHTO (American Association of State Highway and Transportation Officials): Washington, DC, USA, 2011. [Google Scholar]
- Echaveguren, T.; Bustos, M.; De Solminihac, H. Assessment of horizontal curves of an existing road using reliability concepts. Can. J. Civ. Eng. 2005, 32, 1030–1038. [Google Scholar] [CrossRef]
- Hurtado, A. Estudio del Coeficiente de Fricción en Asfalto con Presencia de Hielo y Arena Empleando el péndulo Deslizante. Master’s Thesis, Instituto Politécnico Nacional, Ciudad de México, México, 2017. [Google Scholar]



| Geometric Model | Curvature Parameter | Maximum Speed |
|---|---|---|
| “n & t”/unrotated cylindrical-polar system (Equation (7)/Equation (16)) | R | |
| Rotated cylindrical-polar system (Equation (13)) | r | |
| Rotated cylindrical-polar system (Equation (14)) | R | |
| Spherical system (Equation (21)) | R | |
| Spherical system (Equation (22)) | r |
| Parameter | Parametric Range | Parameter Mean |
|---|---|---|
| Curvature radius | ∼ | |
| Super-elevation | ∼ | |
| Maximum speed | ∼ |
| Pavement Particular Conditions | Parametric Range | Parameter Mean | Mean Particle Diameter |
|---|---|---|---|
| Iced, no sand | ∼ | Not applicable. | |
| Dry, sandy | ∼ | ∼ | |
| Dry, sandy | ∼ | ∼ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anaya Rivera, E.; Isaza, C.; Ramirez-Gutierrez, C.F.; Zavala-De Paz, J.P.; Ibarra Tapia, P.R.; Rizzo-Sierra, J.A. Analyzing the Impact of Geometrophysical Modeling on Highway Design Speeds: A Comparative Study for Mexico’s Case. Appl. Sci. 2024, 14, 4064. https://doi.org/10.3390/app14104064
Anaya Rivera E, Isaza C, Ramirez-Gutierrez CF, Zavala-De Paz JP, Ibarra Tapia PR, Rizzo-Sierra JA. Analyzing the Impact of Geometrophysical Modeling on Highway Design Speeds: A Comparative Study for Mexico’s Case. Applied Sciences. 2024; 14(10):4064. https://doi.org/10.3390/app14104064
Chicago/Turabian StyleAnaya Rivera, Ely, Cesar Isaza, Cristian Felipe Ramirez-Gutierrez, J. P. Zavala-De Paz, Pamela Rocío Ibarra Tapia, and Jose Amilcar Rizzo-Sierra. 2024. "Analyzing the Impact of Geometrophysical Modeling on Highway Design Speeds: A Comparative Study for Mexico’s Case" Applied Sciences 14, no. 10: 4064. https://doi.org/10.3390/app14104064








