Ternary Hybrid Nanofluid Flow Containing Gyrotactic Microorganisms over Three Different Geometries with Cattaneo–Christov Model
Abstract
:1. Introduction
- The mathematical flow model of THNF (Al2O3-Cu-CNT/water) over three different geometries (a flat plate, a wedge, and a cone).
- The application of CCHM in the THNF flow.
- The significance of motile GM in THNF (Al2O3-Cu-CNT/water).
- Investigating the HT rate of THNF flow over three different geometries (a flat plate, a wedge, and a cone) and finding the condition/geometries under present modeling for which THNF has the maximum HT rate.
- Comparison of the HT rate of THNF flow with the HT rate of HNF and NF in the case of all three geometries.
2. Flow Model and Governing Equations
2.1. Flow Assumptions and Mathematical Model
- (a)
- THNF flow toward cone: n = 1 and α ≠ 0.
- (b)
- THNF flow toward wedge: n = 0 and α ≠ 0.
- (c)
- THNF flow toward flat plate: n = 0 and α ≠ 0.
2.2. Properties of Ternary Hybrid Nanofluid
2.3. Conversion of the Model Equations with Similarity Transformation
3. Engineering Parameters
4. Methodology of Numerical Approach
5. Results and Discussion
5.1. Discussion of Velocity Profiles, Velocity Boundary Layer Patterns, and Streamlines
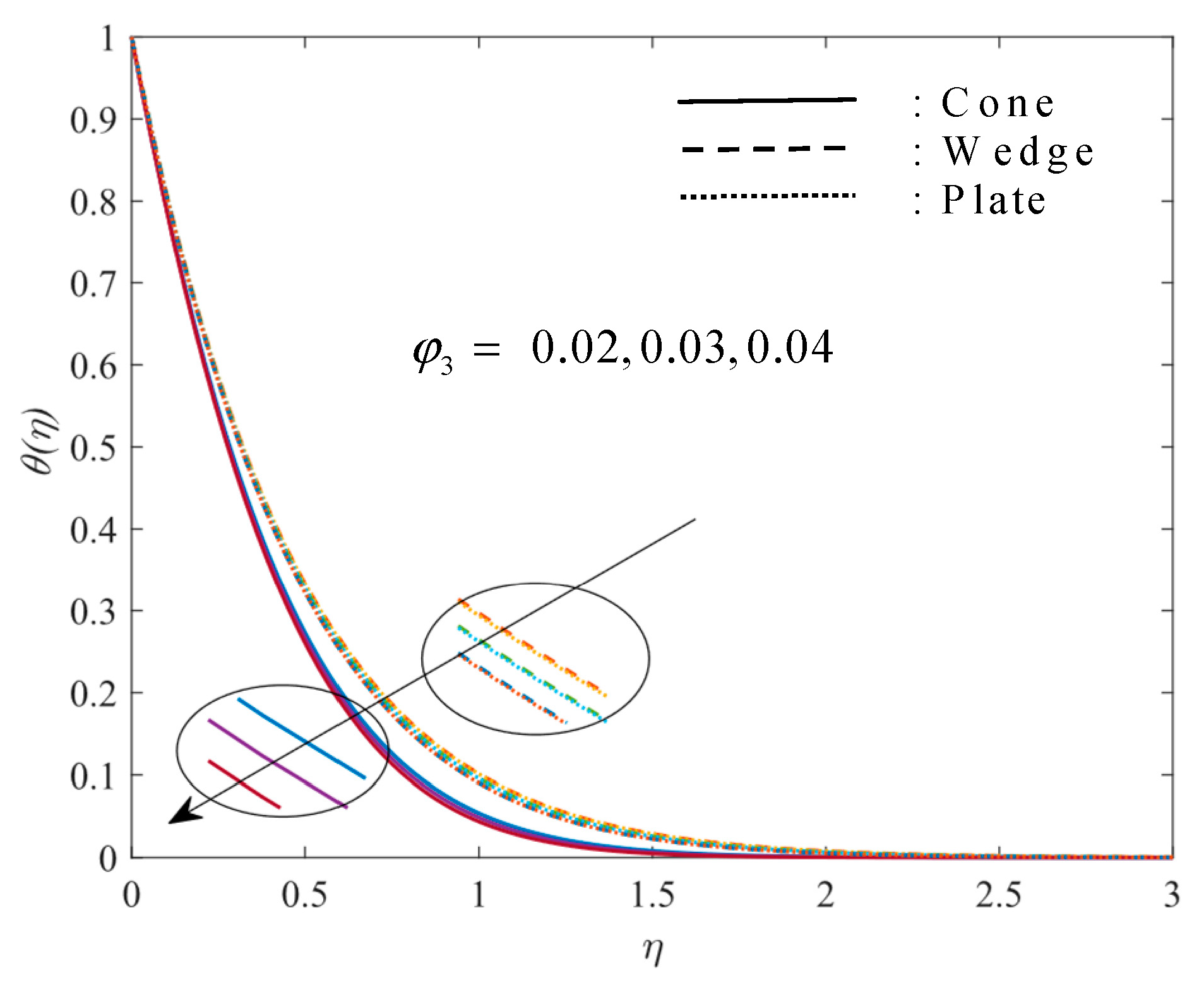
5.2. Discussion of Temperature Profiles
5.3. Discussion of Nanoparticles Concentration and Microorganisms Concentration
5.4. Discussion of Nusselt Number, Sherwood Number, and Motile Microorganisms’ Density Gradient
6. Conclusions
- ➢
- A stronger application of suction causes the thickness of the momentum boundary layer to reduce.
- ➢
- The temperature of THNF increases with higher radiation parameter and heat source/sink parameter.
- ➢
- The increasing value of the thermal relaxation parameter corresponding to the Cattaneo–Christov theory acts to enhance the heat transmission rate.
- ➢
- The microorganism concentration profile decreases with higher bioconvection Lewis number.
- ➢
- The heat transmission rate is highest for the flow toward the cone.
- ➢
- Mass transmission rate and microbe density gradient are highest for the flow toward the wedge.
Future Scope of Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Thermal conductivity | TC |
| Heat transmission | HT |
| Nanoparticles | NPs |
| Base fluid | BF |
| Nanofluids | NFs |
| Nanoparticles volume fraction | NVF |
| Hybrid nanofluids | HNFs |
| Ternary hybrid nanofluid | THNF |
| Cattaneo–Christov heat flux model | CCHM |
| Gyrotactic microorganism | GM |
| Aluminum oxide | Al2O3 |
| Copper | Cu |
| Carbon nanotube | CNTs |
| Boundary layer region | BLR |
References
- Choi, S.U.S. Enhancing Thermal Conductivity of Fluids with Nanoparticles. Am. Soc. Mech. Eng. Fluids Eng. Div. FED 1995, 231, 99–105. [Google Scholar]
- Sahoo, R.R. Thermo-Hydraulic Characteristics of Radiator with Various Shape Nanoparticle-Based Ternary Hybrid Nanofluid. Powder Technol. 2020, 370, 19–28. [Google Scholar] [CrossRef]
- Adun, H.; Kavaz, D.; Dagbasi, M. Review of Ternary Hybrid Nanofluid: Synthesis, Stability, Thermophysical Properties, Heat Transfer Applications, and Environmental Effects. J. Clean. Prod. 2021, 328, 129525. [Google Scholar] [CrossRef]
- Xuan, Z.; Zhai, Y.; Ma, M.; Li, Y.; Wang, H. Thermo-Economic Performance and Sensitivity Analysis of Ternary Hybrid Nanofluids. J. Mol. Liq. 2021, 323, 114889. [Google Scholar] [CrossRef]
- Sahoo, R.R.; Kumar, V. Development of a New Correlation to Determine the Viscosity of Ternary Hybrid Nanofluid. Int. Commun. Heat Mass Transf. 2020, 111, 104451. [Google Scholar] [CrossRef]
- Sahoo, R.R. Experimental Study on the Viscosity of Hybrid Nanofluid and Development of a New Correlation. Heat Mass Transf. 2020, 56, 3023–3033. [Google Scholar] [CrossRef]
- Animasaun, I.L.; Yook, S.J.; Muhammad, T.; Mathew, A. Dynamics of Ternary-Hybrid Nanofluid Subject to Magnetic Flux Density and Heat Source or Sink on a Convectively Heated Surface. Surf. Interfaces 2022, 28, 101654. [Google Scholar] [CrossRef]
- Alanazi, M.M.; Ahmed Hendi, A.; Ahammad, N.A.; Ali, B.; Majeed, S.; Shah, N.A. Significance of Ternary Hybrid Nanoparticles on the Dynamics of Nanofluids over a Stretched Surface Subject to Gravity Modulation. Mathematics 2023, 11, 809. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Ameer, N.A.; Kiran, S.; Nehad, A.S.; Se-jin, Y.; Dinesh, M.K. Nonlinear linear movements of axisymmetric ternary hybrid nanofluids in a thermally radiated expanding or contracting permeable Darcy Walls with different shapes and densities: Simple linear regression. Int. Commun. Heat Mass Transfer 2022, 135, 106110. [Google Scholar] [CrossRef]
- Ramzan, M.; Dawar, A.; Saeed, A.; Kumam, P.; Sitthithakerngkiet, K.; Lone, S.A. Analysis of the Partially Ionized Kerosene Oil-Based Ternary Nanofluid Flow over a Convectively Heated Rotating Surface. Open Phys. 2022, 20, 507–525. [Google Scholar] [CrossRef]
- Fourier, J. Théorie Analytique de La Chaleur; Chez Firmin Didot: Paris, France, 1822. [Google Scholar]
- Cattaneo, C. Sulla Conduzione Del Calore. Atti Sem. Mat. Fis. Univ. Modena 1948, 3, 83–101. [Google Scholar]
- Christov, C.I. On Frame Indifferent Formulation of the Maxwell-Cattaneo Model of Finite-Speed Heat Conduction. Mech. Res. Commun. 2009, 36, 481–486. [Google Scholar] [CrossRef]
- Venkateswarlu, S.; Varma, S.V.K.; Durga Prasad, P. MHD Flow of MoS2 and MgO Water-Based Nanofluid through Porous Medium over a Stretching Surface with Cattaneo-Christov Heat Flux Model and Convective Boundary Condition. Int. J. Ambient Energy 2020, 43, 2940–2949. [Google Scholar] [CrossRef]
- Rawat, S.K.; Kumar, M. Cattaneo–Christov Heat Flux Model in Flow of Copper Water Nanofluid Through a Stretching/Shrinking Sheet on Stagnation Point in Presence of Heat Generation/Absorption and Activation Energy. Int. J. Appl. Comput. Math. 2020, 6, 112. [Google Scholar] [CrossRef]
- Ramzan, M.; Gul, H.; Baleanu, D.; Nisar, K.S.; Malik, M.Y. Role of Cattaneo–Christov Heat Flux in an MHD Micropolar Dusty Nanofluid Flow with Zero Mass Flux Condition. Sci. Rep. 2021, 11, 19528. [Google Scholar] [CrossRef]
- Lv, Y.P.; Gul, H.; Ramzan, M.; Chung, J.D.; Bilal, M. Bioconvective Reiner–Rivlin Nanofluid Flow over a Rotating Disk with Cattaneo–Christov Flow Heat Flux and Entropy Generation Analysis. Sci. Rep. 2021, 11, 15859. [Google Scholar] [CrossRef]
- Abderrahmane, A.; Qasem, N.A.A.; Younis, O.; Marzouki, R.; Mourad, A.; Shah, N.A.; Chung, J.D. MHD Hybrid Nanofluid Mixed Convection Heat Transfer and Entropy Generation in a 3-D Triangular Porous Cavity with Zigzag Wall and Rotating Cylinder. Mathematics 2022, 10, 769. [Google Scholar] [CrossRef]
- Kumar, M.D.; Raju, C.S.K.; Sajjan, K.; El-Zahar, E.R.; Shah, N.A. Linear and quadratic convection on 3D flow with transpiration and hybrid nanoparticles. Int. Commun. Heat Mass Transfer 2022, 134, 105995. [Google Scholar] [CrossRef]
- Sajjan, K.; Shah, N.A.; Ahammad, N.A.; Raju, C.S.K.; Kumar, M.D.; Weera, W. Nonlinear Boussinesq and Rosseland approximations on 3D flow in an interruption of Ternary nanoparticles with various shapes of densities and conductivity properties. AIMS Math. 2022, 7, 18416–18449. [Google Scholar] [CrossRef]
- Kuznetsov, A.V. Bio-Thermal Convection Induced by Two Different Species of Microorganisms. Int. Commun. Heat Mass Transf. 2011, 38, 548–553. [Google Scholar] [CrossRef]
- Shi, Q.-H.H.; Hamid, A.; Khan, M.I.; Kumar, R.N.; Gowda, R.J.P.P.; Prasannakumara, B.C.; Shah, N.A.; Khan, S.U.; Chung, J.D.; Naveen Kumar, R.; et al. Numerical Study of Bio-Convection Flow of Magneto-Cross Nanofluid Containing Gyrotactic Microorganisms with Activation Energy. Sci. Rep. 2021, 11, 16030. [Google Scholar] [CrossRef] [PubMed]
- Al-Khaled, K.; Ullah Khan, S. Thermal Aspects of Casson Nanoliquid with Gyrotactic Microorganisms, Temperature-Dependent Viscosity, and Variable Thermal Conductivity: Bio-Technology and Thermal Applications. Inventions 2020, 5, 39. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Marin, M.; Zeeshan, A.; Ellahi, R.; Abdelsalam, S.I. Swimming of Motile Gyrotactic Microorganisms and Nanoparticles in Blood Flow Through Anisotropically Tapered Arteries. Front. Phys. 2020, 8, 95. [Google Scholar] [CrossRef] [Green Version]
- Kairi, R.R.; Shaw, S.; Roy, S.; Raut, S. Thermosolutal Marangoni Impact on Bioconvection in Suspension of Gyrotactic Microorganisms over an Inclined Stretching Sheet. J. Heat Transf. 2021, 143, 031201. [Google Scholar] [CrossRef]
- Ali, A.; Sarkar, S.; Das, S.; Jana, R.N. Investigation of Cattaneo–Christov Double Diffusions Theory in Bioconvective Slip Flow of Radiated Magneto-Cross-Nanomaterial Over Stretching Cylinder/Plate with Activation Energy. Int. J. Appl. Comput. Math. 2021, 7, 208. [Google Scholar] [CrossRef]
- Mishra, A.; Kumar, M. Numerical Analysis of MHD Nanofluid Flow over a Wedge, Including Effects of Viscous Dissipation and Heat Generation/Absorption, Using Buongiorno Model. Heat Transf. 2021, 50, 8453–8474. [Google Scholar] [CrossRef]
- Yaseen, M.; Rawat, S.K.; Kumar, M. Falkner–Skan Problem for a Stretching or Shrinking Wedge With Nanoparticle Aggregation. J. Heat Transf. 2022, 144, 102501. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Mackolil, J. Flow of Nanoliquid Past a Vertical Plate with Novel Quadratic Thermal Radiation and Quadratic Boussinesq Approximation: Sensitivity Analysis. Int. Commun. Heat Mass Transf. 2021, 120, 105040. [Google Scholar] [CrossRef]
- Gumber, P.; Yaseen, M.; Kumar, S.; Kumar, M. Heat Transfer in Micropolar Hybrid Nanofluid Flow Past a Vertical Plate in the Presence of Thermal Radiation and Suction/Injection Effects. Partial Differ. Equ. Appl. Math. 2022, 5, 100240. [Google Scholar] [CrossRef]
- Rawat, S.K.; Upreti, H.; Kumar, M. Comparative Study of Mixed Convective MHD Cu-Water Nanofluid Flow over a Cone and Wedge Using Modified Buongiorno’s Model in Presence of Thermal Radiation and Chemical Reaction via Cattaneo-Christov Double Diffusion Model. J. Appl. Comput. Mech. 2021, 7, 1383–1402. [Google Scholar] [CrossRef]
- Sandeep, N.; Reddy, M.G. Heat Transfer of Nonlinear Radiative Magnetohydrodynamic Cu-Water Nanofluid Flow over Two Different Geometries. J. Mol. Liq. 2017, 225, 87–94. [Google Scholar] [CrossRef]
- Reddy, M.G.; Rani, M.V.V.N.L.S.; Kumar, K.G.; Prasannakumara, B.C. Cattaneo–Christov Heat Flux and Non-Uniform Heat-Source/Sink Impacts on Radiative Oldroyd-B Two-Phase Flow across a Cone/Wedge. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 95. [Google Scholar] [CrossRef]
- Jayachandra Babu, M.; Sandeep, N.; Saleem, S. Free Convective MHD Cattaneo-Christov Flow over Three Different Geometries with Thermophoresis and Brownian Motion. Alex. Eng. J. 2017, 56, 659–669. [Google Scholar] [CrossRef]
- Garia, R.; Rawat, S.K.; Kumar, M.; Yaseen, M. Hybrid Nanofluid Flow over Two Different Geometries with Cattaneo–Christov Heat Flux Model and Heat Generation: A Model with Correlation Coefficient and Probable Error. Chin. J. Phys. 2021, 74, 421–439. [Google Scholar] [CrossRef]
- Arif, M.; Kumam, P.; Kumam, W.; Mostafa, Z. Heat Transfer Analysis of Radiator Using Different Shaped Nanoparticles Water-Based Ternary Hybrid Nanofluid with Applications: A Fractional Model. Case Stud. Therm. Eng. 2022, 31, 101837. [Google Scholar] [CrossRef]
- Elnaqeeb, T.; Animasaun, I.L.; Shah, N.A. Ternary-Hybrid Nanofluids: Significance of Suction and Dual-Stretching on Three-Dimensional Flow of Water Conveying Nanoparticles with Various Shapes and Densities. Z. Naturforsch.—Sect. A J. Phys. Sci. 2021, 76, 231–243. [Google Scholar] [CrossRef]
- Vajravelu, K.; Nayfeh, J. Hydromagnetic Convection at a Cone and a Wedge. Int. Commun. Heat Mass Transf. 1992, 19, 701–710. [Google Scholar] [CrossRef]
- Yaseen, M.; Rawat, S.K.; Kumar, M. Cattaneo–Christov Heat Flux Model in Darcy–Forchheimer Radiative Flow of MoS2–SiO2/Kerosene Oil between Two Parallel Rotating Disks. J. Therm. Anal. Calorim. 2022, 147, 10865–10887. [Google Scholar] [CrossRef]
- Shampine, L.F.; Gladwell, I.; Thompson, S. Solving ODEs with MATLAB; Cambridge University Press: Cambridge, UK, 2003; ISBN 9780511615542. [Google Scholar]


























| ρ (kg/m3) | Cp (J/kgK) | k (W/mK) | β (K−1) | Shape | Sphericity | |
|---|---|---|---|---|---|---|
| Water | 997.1 | 4179 | 0.613 | 21 | ||
| Al2O3 | 3970 | 765 | 40 | 0.85 | Spherical | ψ = 1 |
| Cu | 8933 | 385 | 401 | 1.67 | Platelet | ψ = 0.612 |
| CNT | 2600 | 425 | 6600 | 1.6 × 10−6 | Cylindrical | ψ = 0.52 |
| Density | ||
| Heat capacitance | ||
| Modified Maxwell model: | where, is shape factor. | |
| Nanoparticle—1 | (Spherical) | |
| Nanoparticle—2 | (Platelet) | |
| Nanoparticle—3 | (Cylindrical) | |
| Viscosity | ||
| Thermal conductivity | Where | |
| Q | Pr | Gr | M | s | ||||
|---|---|---|---|---|---|---|---|---|
| −5 | 0.3 | −0.5 | 1 | −2.1 | −0.155592 | −0.15570252 | −2.237475 | −2.23538986 |
| −5 | 0.3 | −0.5 | 1 | 2.1 | −0.156001 | −0.15588966 | −2.232780 | −2.23418090 |
| −5 | 0.3 | −0.5 | 3 | 2.1 | −0.126400 | −0.12634921 | −2.233732 | −2.23472524 |
| −5 | 1.0 | 0.5 | 3 | 2.1 | 0.125260 | 0.12541914 | −2.245321 | −2.24047000 |
| Cone | Wedge | Plate | ||||||||||||||||
| Pe | Le | Lb | Q | Rd | S | Nu | Sh | Nm | Nu | Sh | Nm | Nu | Sh | Nm | ||||
| 0.1 | 0.2 | 1.5 | 0.01 | 1.5 | 0.5 | 0.2 | −2 | 10 | 0.1 | 24.92767 | −1.51382 | −0.87947 | 23.00199 | −1.09132 | −0.6332 | 23.02106 | −1.09284 | −0.63419 |
| 0.2 | - | - | −1.03107 | - | - | −0.74255 | - | - | −0.74368 | |||||||||
| 0.4 | - | - | −1.33868 | - | - | −0.96453 | - | - | −0.96592 | |||||||||
| 0.1 | 0.7 | - | - | −0.93948 | - | - | −0.67622 | - | - | −0.67727 | ||||||||
| 1.7 | - | - | −1.0595 | - | - | −0.76227 | - | - | −0.76342 | |||||||||
| 0.2 | 0.9 | 20.81458 | −1.51501 | −0.88056 | 19.29351 | −1.09256 | −0.63414 | 19.31295 | −1.09457 | −0.63551 | ||||||||
| 1.3 | 23.60737 | −1.51414 | −0.87976 | 21.80354 | −1.09167 | −0.63346 | 21.82288 | −1.09332 | −0.63456 | |||||||||
| 1.5 | 0.06 | - | −1.38953 | −0.86634 | - | −1.04645 | −0.62838 | - | −1.04774 | −0.62935 | ||||||||
| 0.16 | - | −1.16796 | −0.84311 | - | −0.96177 | −0.6193 | - | −0.96266 | −0.62024 | |||||||||
| 0.01 | 2 | - | −1.81643 | −0.91215 | - | −1.3191 | −0.65807 | - | −1.32073 | −0.65908 | ||||||||
| 3 | - | −2.3356 | −0.96938 | - | −1.71464 | −0.70207 | - | −1.71641 | −0.70309 | |||||||||
| 1.5 | 0.6 | - | - | −0.97675 | - | - | −0.69807 | - | - | −0.69919 | ||||||||
| 0.7 | - | - | −1.06895 | - | - | −0.76131 | - | - | −0.76253 | |||||||||
| 0.5 | −1.8 | 24.55437 | −1.47761 | −0.85227 | 22.49837 | −1.04949 | −0.60575 | 22.28255 | −1.03021 | −0.59317 | ||||||||
| 2.2 | 25.26119 | −1.5448 | −0.90259 | 23.4335 | −1.12445 | −0.65503 | 23.61331 | −1.13766 | −0.66375 | |||||||||
| 0.2 | −1.4 | 21.88554 | −1.51457 | −0.88013 | 20.27092 | −1.09219 | −0.63385 | 20.294 | −1.09404 | −0.6351 | ||||||||
| −0.8 | 18.43186 | −1.51581 | −0.88131 | 17.15315 | −1.09365 | −0.63502 | 17.18372 | −1.09606 | −0.63672 | |||||||||
| 0.4 | 7.816058 | −1.53274 | −0.90268 | 7.173743 | −1.11078 | −0.65175 | 7.408173 | −1.11788 | −0.65803 | |||||||||
| −2 | 12 | 26.66715 | −1.51439 | −0.87998 | 24.58693 | −1.09197 | −0.63368 | 24.61154 | −1.09374 | −0.63487 | ||||||||
| 14 | 28.25102 | −1.51495 | −0.88049 | 26.03504 | −1.0926 | −0.63417 | 26.06564 | −1.09462 | −0.63555 | |||||||||
| 16 | 29.70916 | −1.51549 | −0.88101 | 27.37275 | −1.09321 | −0.63465 | 27.40974 | −1.09547 | −0.63623 | |||||||||
| 10 | −0.1 | 22.27847 | −1.287 | −0.77905 | 19.99349 | −0.85639 | −0.53176 | 20.0157 | −0.85824 | −0.53294 | ||||||||
| 0.1 | 24.92767 | −1.51382 | −0.87947 | 23.00199 | −1.09132 | −0.6332 | 23.02106 | −1.09284 | −0.63419 | |||||||||
| 0.3 | 27.94773 | −1.7543 | −0.98592 | 26.47821 | −1.3467 | −0.74315 | 26.49433 | −1.3479 | −0.74397 | |||||||||
| . | Cone | Wedge | Plate | ||||||||
| Nu | Sh | Nm | Nu | Sh | Nm | Nu | Sh | Nm | |||
| 0.02 | 0.02 | 0.02 | 24.92767 | −1.51382 | −0.87947 | 23.00199 | −1.09132 | −0.6332 | 23.02106 | −1.09284 | −0.63419 |
| 0.03 | 24.84579 | −1.41239 | −0.8171 | 22.92604 | −1.01785 | −0.58918 | 22.94572 | −1.01933 | −0.59014 | ||
| 0.04 | 24.78749 | −1.33885 | −0.77203 | 22.87163 | −0.96459 | −0.55737 | 22.89167 | −0.96603 | −0.5583 | ||
| 0.02 | 0.03 | 25.06144 | −1.67807 | −0.98093 | 23.12018 | −1.21024 | −0.7047 | 23.13655 | −1.21166 | −0.70564 | |
| 0.04 | 25.26947 | −1.98846 | −1.17404 | 23.30667 | −1.43523 | −0.84079 | 23.31994 | −1.43655 | −0.84169 | ||
| 0.02 | 0.03 | 25.15922 | −1.86527 | −1.09724 | 23.20391 | −1.346 | −0.78672 | 23.21942 | −1.34746 | −0.78771 | |
| 0.04 | 25.4086 | −2.36089 | −1.40762 | 23.42386 | −1.70561 | −1.00551 | 23.43616 | −1.70703 | −1.00649 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yaseen, M.; Rawat, S.K.; Shah, N.A.; Kumar, M.; Eldin, S.M. Ternary Hybrid Nanofluid Flow Containing Gyrotactic Microorganisms over Three Different Geometries with Cattaneo–Christov Model. Mathematics 2023, 11, 1237. https://doi.org/10.3390/math11051237
Yaseen M, Rawat SK, Shah NA, Kumar M, Eldin SM. Ternary Hybrid Nanofluid Flow Containing Gyrotactic Microorganisms over Three Different Geometries with Cattaneo–Christov Model. Mathematics. 2023; 11(5):1237. https://doi.org/10.3390/math11051237
Chicago/Turabian StyleYaseen, Moh, Sawan Kumar Rawat, Nehad Ali Shah, Manoj Kumar, and Sayed M. Eldin. 2023. "Ternary Hybrid Nanofluid Flow Containing Gyrotactic Microorganisms over Three Different Geometries with Cattaneo–Christov Model" Mathematics 11, no. 5: 1237. https://doi.org/10.3390/math11051237





