A Comparative Review of Models for All-Solid-State Li-Ion Batteries
Abstract
:1. Introduction
2. Models and Their Governing Equations
2.1. One-Dimensional Single-Ion Conduction Models [19]
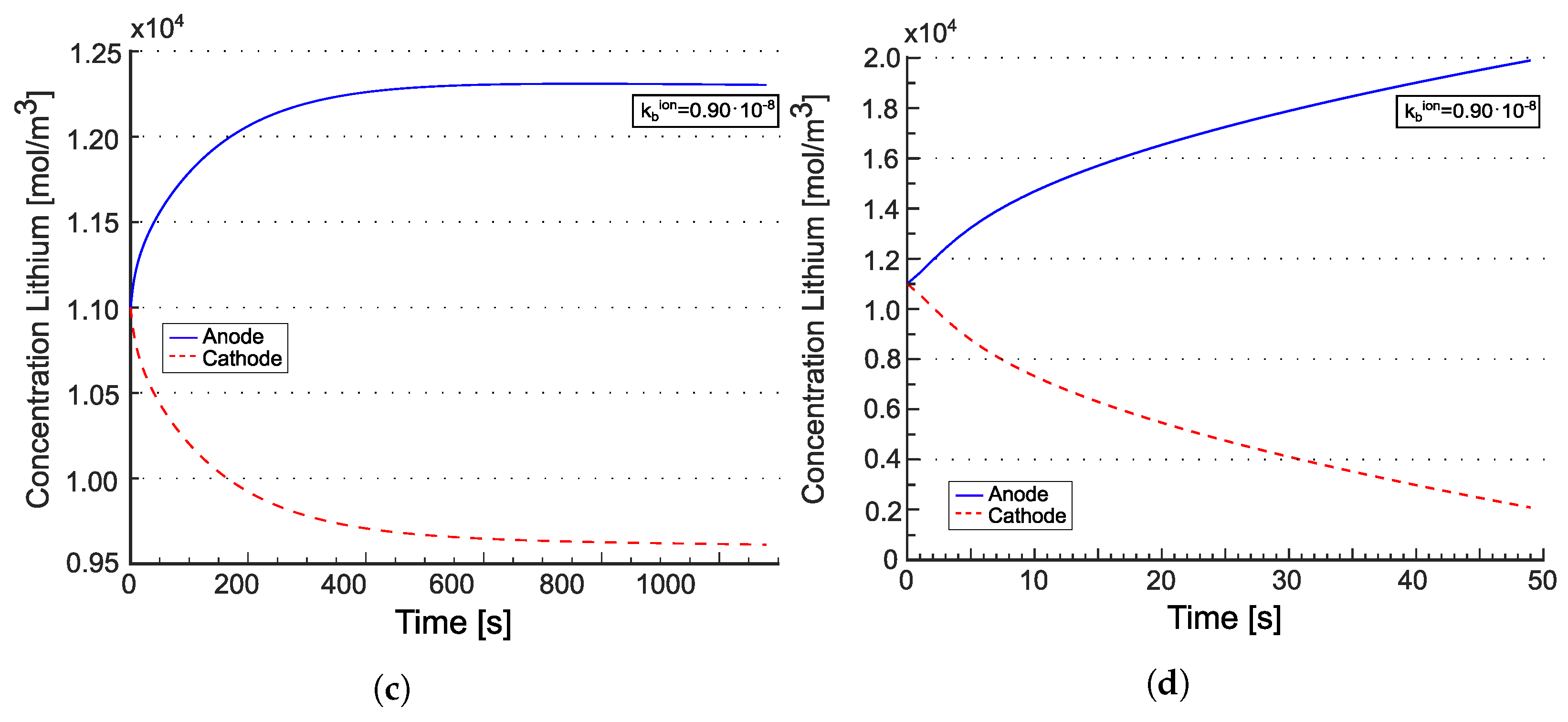
2.2. An Advanced Framework for Solid-Electrolyte Intercalation Batteries [20]
2.3. An Advanced All-Solid-State Li-Ion Battery Model [21]
2.4. Two-Mechanism Model for All-Solid-State Lithium-Ion Batteries
3. Benchmark Comparison
4. Final Remarks and Further Developments
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Analytical OCP Simulations

Appendix B. Material and Geometrical Parameters Used for Model Validation
| Parameter | Value | Unit | Description |
|---|---|---|---|
| T | Temperature | ||
| Thickness of the anode | |||
| Thickness of the electrolyte | |||
| Thickness of the cathode | |||
| Thickness of the positive collector | |||
| A | Geometrical surface area | ||
| Maximum concentration of ions in the electrode | |||
| Electrical conductivities in the lithium anode | |||
| Electrical conductivities in the current collector | |||
| () | Lithium-ion generation reaction rate constant for Equation (3) | ||
| Lithium-ion recombination reaction rate constant for Equation (3) | |||
| () | Lithium-ion generation reaction rate constant for Equation (35) | ||
| Lithium-ion recombination reaction rate constant for Equation (35) | |||
| Double-layer capacity per unit area of anode | |||
| Double-layer capacity per unit area of cathode | |||
| - | Charge transfer coefficient for the negative electrode | ||
| - | Charge transfer coefficient for the positive electrode | ||
| Diffusion coefficient for ions in the electrolyte | |||
| Diffusion coefficient for ions in the electrolyte | |||
| Diffusion coefficient for ions in the cathode | |||
| Standard reaction rate constant for forward reaction in Equation (1) | |||
| Standard reaction rate constant for forward reaction in Equation (2) | |||
| - | Fraction of mobile ions in the electrolyte in equilibrium | ||
| Maximal lithium concentration in the electrolyte | |||
| - | Relative permittivity in the electrolyte |
References
- Schnell, J.; Günther, T.; Knoche, T.; Vieider, C.; Köhler, L.; Just, A.; Keller, M.; Passerini, S.; Reinhart, G. All-solid-state lithium-ion and lithium metal batteries—Paving the way to large-scale production. J. Power Sources 2018, 382, 160–175. [Google Scholar] [CrossRef]
- Zheng, F.; Kotobuki, M.; Song, S.; Lai, M.; Lu, L. Review on solid electrolytes for all-solid-state lithium-ion batteries. J. Power Sources 2018, 389, 198–213. [Google Scholar] [CrossRef]
- Arreaga-Salas, D.E.; Sra, A.K.; Roodenko, K.; Chabal, Y.J.; Hinkle, C.L. Progression of solid electrolyte interphase formation on hydrogenated amorphous silicon anodes for lithium-ion batteries. J. Phys. Chem. C 2012, 116, 9072–9077. [Google Scholar] [CrossRef]
- Pasta, M.; Armstrong, D.; Brown, Z.; Bu, J.; Castell, M.; Chen, P.; Cocks, A.; Corr, S.; Cussen, E.; Darnbrough, E.; et al. 2020 roadmap on solid-state batteries. J. Phys. Energy 2020, 2, 032008. [Google Scholar] [CrossRef]
- Santhanagopalan, D.; Qian, D.; McGilvray, T.; Wang, Z.; Camino, F.; Graetz, J.; Dudney, N.; Meng, Y. Interface limited lithium transport in solidstate batteries. J. Phys. Chem. Lett. 2014, 5, 298–303. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Jiang, M.; Zhou, T.; Raijmakers, L.; Vezhlev, E.; Wu, B.; Schuelli, T.; Danilov, D.; Wei, Y.; Eichel, R.; et al. Interface Aspects in All-Solid-State Li-Based Batteries Reviewed. Adv. Energy Mater. 2021, 11, 2003939. [Google Scholar] [CrossRef]
- Zhang, F.; Huang, Q.; Tang, Z.; Li, A.; Shao, Q.; Zhang, L.; Li, X.; Zhang, J. A review of mechanics-related material damages in all-solid-state batteries: Mechanisms, performance impacts and mitigation strategies. Nano Energy 2020, 70, 104545. [Google Scholar] [CrossRef]
- Tian, H.K.; Qi, Y. Simulation of the Effect of Contact Area Loss in All-Solid-State Li-Ion Batteries. J. Electrochem. Soc. 2017, 164, 3512–3521. [Google Scholar] [CrossRef]
- Waldmann, T.; Hogg, B.; Wohlfahrt-Mehrens, M. Li plating as unwanted side reaction in commercial Li-ion cells—A review. J. Power Sources 2018, 384, 107–124. [Google Scholar] [CrossRef]
- Porz, L.; Swamy, T.; Sheldon, B.; Rettenwander, D.; Frömling, T.; Thaman, H.; Berendts, S.; Uecker, R.; Carter, W.; Chiang, Y. Mechanism of Lithium Metal Penetration through Inorganic Solid Electrolytes. Adv. Energy Mater. 2017, 7, 1701003. [Google Scholar] [CrossRef]
- Shishvan, S.; Fleck, N.; McMeeking, R.; Deshpande, V. Growth rate of lithium filaments in ceramic electrolytes. Acta Mater. 2020, 196, 444–455. [Google Scholar] [CrossRef]
- Fan, L.; Wei, S.; Li, S.; Li, Q.; Lu, Y. Recent Progress of the Solid-State Electrolytes for High-Energy Metal-Based Batteries. Adv. Energy Mater. 2018, 8, 1702657. [Google Scholar] [CrossRef]
- Yuan, H.; Luan, J.; Yang, Z.; Zhang, J.; Wu, Y.; Lu, Z.; Liu, H. Single Lithium-Ion Conducting Solid Polymer Electrolyte with Superior Electrochemical Stability and Interfacial Compatibility for Solid-State Lithium Metal Batteries. ACS Appl. Mater. Interfaces 2020, 12, 7249–7256. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Yao, Y.; Ou, J.; Li, M.; Luo, D.; Dou, H.; Li, Z.; Amine, K.; Yu, A.; Chen, Z. A review of composite solid-state electrolytes for lithium batteries: Fundamentals, key materials and advanced structures. Chem. Soc. Rev. 2020, 49, 8790–8839. [Google Scholar] [CrossRef] [PubMed]
- Bielefeld, A.; Weber, D.; Janek, J. Microstructural modeling of composite cathodes for all solid state batteries. J. Phys. Chem. C 2019, 123, 1626–1634. [Google Scholar] [CrossRef]
- Cao, C.; Li, Z.; Wang, X.; Zhao, X.; Han, W. Recent advances in inorganic solid electrolytes for lithium batteries. Front. Energy Res. 2014, 2, 25–35. [Google Scholar] [CrossRef]
- Grazioli, D.; Magri, M.; Salvadori, A. Computational modeling of Li-ion batteries. Comput. Mech. 2016, 58, 889–909. [Google Scholar] [CrossRef]
- Li, G.; Monroe, C.W. Multiscale Lithium-Battery Modeling from Materials to Cells. Annu. Rev. Chem. Biomol. 2020, 11, 277–310. [Google Scholar] [CrossRef] [PubMed]
- Fabre, S.; Guy-Bouyssou, D.; Bouillon, P.; Le Cras, F.; Delacourt, C. Charge/Discharge Simulation of an All-Solid-State Thin-Film Battery Using a One-Dimensional Model. J. Electrochem. Soc. 2012, 159, A104–A115. [Google Scholar] [CrossRef]
- Landstorfer, M.; Funken, S.; Jacob, T. An advanced model framework for solid electrolyte intercalation batteries. Phys. Chem. Chem. Phys. 2011, 13, 12817–12825. [Google Scholar] [CrossRef] [PubMed]
- Raijmakers, L.; Danilov, D.; Eichel, R.; Notten, P. An advanced all-solid-state Li-ion battery model. Electrochim. Acta 2020, 330, 135147. [Google Scholar] [CrossRef]
- Cabras, L.; Danilov, D.; Subber, W.; Oancea, V.; Salvadori, A. A two-mechanism and multiscale compatible approach for solid state electrolytes of (Li-ion) batteries. J. Energy Storage 2022, 48, 103842. [Google Scholar] [CrossRef]
- Salvadori, A.; Grazioli, D.; Geers, M. Governing equations for a two-scale analysis of Li-ion battery cells. Int. J. Solids Struct. 2015, 59, 90–109. [Google Scholar] [CrossRef]
- Mykhaylov, M.; Ganser, M.; Klinsmann, M.; Hildebrand, F.; Guz, I.; McMeeking, R. An elementary 1-dimensional model for a solid state lithium-ion battery with a single ion conductor electrolyte and a lithium metal negative electrode. J. Mech. Phys. Solids 2019, 123, 207–221. [Google Scholar] [CrossRef]
- Salvadori, A.; Grazioli, D.; Geers, M.; Danilov, D.; Notten, P. A multiscale-compatible approach in modeling ionic transport in the electrolyte of (Lithium ion) batteries. J. Power Sources 2015, 293, 892–911. [Google Scholar] [CrossRef]
- Salvadori, A.; Grazioli, D.; Magri, M.; Geers, M.; Danilov, D.; Notten, P. On the role of saturation in modeling ionic transport in the electrolyte of (Li-ion) batteries. J. Power Sources 2015, 294, 696–710. [Google Scholar] [CrossRef]
- Danilov, D.; Niessen, R.; Notten, P. Modeling All-Solid-State Li-Ion Batteries. J. Electrochem. Soc. 2011, 158, A215–A222. [Google Scholar] [CrossRef]
- Doyle, M.; Newman, J. The use of mathematical modeling in the design of Lithium/polymer battery systems. Electrochim. Acta 1995, 40, 2191–2196. [Google Scholar] [CrossRef]
- Fuller, T.; Doyle, M.; Newman, J. Simulation and Optimization of the Dual Lithium Ion Insertion Cell. J. Electrochem. Soc. 1994, 141, 1–10. [Google Scholar] [CrossRef]
- Salvadori, A.; Bosco, E.; Grazioli, D. A computational homogenization approach for Li-ion battery cells. Part 1—Formulation. J. Mech. Phys. Solids 2014, 65, 114–137. [Google Scholar] [CrossRef]
- Franco, A. Multiscale modelling and numerical simulation of rechargeable Lithium ion batteries: Concepts, methods and challenges. RSC Adv. 2013, 3, 13027–13058. [Google Scholar] [CrossRef]
- Lee, S.; Sastry, A.; Park, J. Study on microstructures of electrodes in Lithium-ion batteries using variational multi-scale enrichment. J. Power Sources 2016, 315, 96–110. [Google Scholar] [CrossRef]
- Franco, A.; Rucci, A.; Brandell, D.; Frayret, C.; Gaberscek, M.; Jankowski, P.; Johansson, P. Boosting Rechargeable Batteries R&D by Multiscale Modeling: Myth or Reality? Chem. Rev. 2019, 119, 4569. [Google Scholar] [PubMed]
- Purkayastha, R.; McMeeking, R. An integrated 2-D model of a Lithium ion battery: The effect of material parameters and morphology on storage particle stress. Comput. Mech. 2012, 50, 209–227. [Google Scholar] [CrossRef]
- Salvadori, A.; McMeeking, R.; Grazioli, D.; Magri, M. A coupled model of transport-reaction-mechanics with trapping. Part I—Small strain analysis. J. Mech. Phys. Solids 2018, 114, 1–30. [Google Scholar] [CrossRef]
- Arricca, M.; Cabras, L.; Serpelloni, M.; Bonanno, C.; McMeeking, R.M.; Salvadori, A. A coupled model of transport-reaction-mechanics with trapping, Part II: Large strain analysis. J. Mech. Phys. Solids 2023, 181, 105425. [Google Scholar] [CrossRef]
- Anand, L. A Cahn-Hilliard-type theory for species diffusion coupled with large elastic-plastic deformations. J. Mech. Phys. Solids 2012, 60, 1983–2002. [Google Scholar] [CrossRef]
- DeHoff, R. Thermodynamic in Material Science; CRC Press—Taylor and Francis: New York, NY, USA, 2006. [Google Scholar]
- Shell, S. Thermodynamics and Statistical Mechanics: An Integrated Approach; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Bohn, E.; Eckl, T.; Kamlah, M.; McMeeking, R. A Model for Lithium Diffusion and Stress Generation in an Intercalation Storage Particle with Phase Change. J. Electrochem. Soc. 2013, 160, A1638–A1652. [Google Scholar] [CrossRef]
- Di Leo, C.; Rejovitzky, E.; Anand, L. A Cahn-Hilliard-type phase-field theory for species diffusion coupled with large elastic deformations: Application to phase-separating Li-ion electrode materials. J. Mech. Phys. Solids 2014, 70, 1–29. [Google Scholar] [CrossRef]
- Bower, A.; Guduru, P.; Chason, E. Analytical solutions for composition and stress in spherical elastic–plastic Lithium-ion electrode particles containing a propagating phase boundary. Int. J. Solids Struct. 2015, 69-70, 328–342. [Google Scholar] [CrossRef]
- Bonnefont, A.; Argoul, F.; Bazant, M. Analysis of diffuse-layer effects on time-dependent interfacial kinetics. J. Electroanal. Chem. 2001, 500, 52–61. [Google Scholar] [CrossRef]
- Bazant, M.; Chu, K.; Bayly, B. Current-voltage relations for elecrochemical thin films. SIAM J. Appl. Math. 2005, 65, 1463–1484. [Google Scholar] [CrossRef]
- Li, D.; Danilov, D.; Xie, J.; Raijmakers, L.; Gao, L.; Yang, Y.; Notten, P. Degradation mechanisms of C6/LiFePO4 batteries: Experimental analyses of calendar aging. Electrochim. Acta 2016, 190, 1124–1133. [Google Scholar] [CrossRef]
- Li, D.; Danilov, D.; Gao, L.; Yang, Y.; Notten, P. Degradation mechanisms of C6/LiFePO4 batteries: Experimental analyses of cycling-induced aging. Electrochim. Acta 2016, 210, 445–455. [Google Scholar] [CrossRef]
- Bard, A.; Faulkner, L. Electrochemical Methods: Fundamentals and Applications, 2nd ed.; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Famprikis, T.; Canepa, P.; Dawson, J.; Islam, M.S.; Masquelier, C. Fundamentals of inorganic solid-state electrolytes for batteries. Nat. Mater. 2019, 18, 1278–1291. [Google Scholar] [CrossRef] [PubMed]
- Cabras, L.; Serpelloni, M.; Salvadori, A. Electro-chemo-mechanics of solid state batteries with lithium plating and stripping. Front. Mater. 2022, 9, 1052617. [Google Scholar] [CrossRef]
- Ganser, M.; Hildebrand, F.; Kamlah, M.; McMeeking, R. A finite strain electro-chemo-mechanical theory for ion transport with application to binary solid electrolytes. J. Mech. Phys. Solids 2019, 125, 681–713. [Google Scholar] [CrossRef]
- Bower, A.; Guduru, P.; Chason, E. A continuum model of deformation, transport and irreversible changes in atomic structure in amorphous Lithium–silicon electrodes. Acta Mater. 2015, 98, 229–241. [Google Scholar] [CrossRef]
- Bucci, G.; Nadimpalli, S.; Sethuraman, V.; Bower, A.; Guduru, P. Measurement and modeling of the mechanical and electrochemical response of amorphous Si thin film electrodes during cyclic lithiation. J. Mech. Phys. Solids 2014, 62, 276–294. [Google Scholar] [CrossRef]
- Magri, M.; Boz, B.; Cabras, L.; Salvadori, A. Quantitative investigation of the influence of electrode morphology in the electro-chemo-mechanical response of li-ion batteries. Electrochim. Acta 2022, 405, 139778. [Google Scholar] [CrossRef]
- Latz, A.; Zausch, J. Multiscale modeling of Li-ion batteries: Thermal aspects. Beilstein J. Nanotechnol. 2015, 6, 987–1007. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Li, Z. Computational Design of Inorganic Solid-State Electrolyte Materials for Lithium-Ion Batteries. Acc. Mater. Res. 2024. [Google Scholar] [CrossRef]
- Maurya, D.K.; Dhanusuraman, R.; Guo, Z.; Angaiah, S. Composite polymer electrolytes: Progress, challenges, and future outlook for sodium-ion batteries. Adv. Compos. Hybrid Mater. 2022, 5, 2651–2674. [Google Scholar] [CrossRef]
- Liao, Y.; Xu, X.; Luo, X.; Ji, S.; Zhao, J.; Liu, J.; Huo, Y. Recent progress in flame-retardant polymer electrolytes for solid-state lithium metal batteries. Batteries 2023, 9, 439. [Google Scholar] [CrossRef]
- Knauth, P.; Tuller, H.L. Solid-state ionics: Roots, status, and future prospects. J. Am. Ceram. Soc. 2002, 85, 1654–1680. [Google Scholar] [CrossRef]
- Takada, K. Progress in solid electrolytes toward realizing solid-state lithium batteries. J. Power Sources 2018, 394, 74–85. [Google Scholar] [CrossRef]
- Xu, R.; Xia, X.; Zhang, S.; Xie, D.; Wang, X.; Tu, J. Interfacial challenges and progress for inorganic all-solid-state lithium batteries. Electrochim. Acta 2018, 284, 177–187. [Google Scholar] [CrossRef]
- Li, X.; Liang, J.; Chen, N.; Luo, J.; Adair, K.R.; Wang, C.; Banis, M.N.; Sham, T.K.; Zhang, L.; Zhao, S.; et al. Water-mediated synthesis of a superionic halide solid electrolyte. Angew. Chem. 2019, 131, 16579–16584. [Google Scholar] [CrossRef]
- Gorai, P.; Famprikis, T.; Singh, B.; Stevanovic, V.; Canepa, P. Devil is in the defects: Electronic conductivity in solid electrolytes. Chem. Mater. 2021, 33, 7484–7498. [Google Scholar] [CrossRef]
- Takada, K.; Ohno, T. Experimental and computational approaches to interfacial resistance in solid-state batteries. Front. Energy Res. 2016, 4, 10. [Google Scholar] [CrossRef]
- Ohta, N.; Takada, K.; Sakaguchi, I.; Zhang, L.; Ma, R.; Fukuda, K.; Osada, M.; Sasaki, T. LiNbO3-coated LiCoO2 as cathode material for all solid-state lithium secondary batteries. Electrochem. Commun. 2007, 9, 1486–1490. [Google Scholar] [CrossRef]
- Takada, K.; Ohta, N.; Zhang, L.; Xu, X.; Hang, B.T.; Ohnishi, T.; Osada, M.; Sasaki, T. Interfacial phenomena in solid-state lithium battery with sulfide solid electrolyte. Solid State Ionics 2012, 225, 594–597. [Google Scholar] [CrossRef]
- Hautier, G.; Jain, A.; Chen, H.; Moore, C.; Ong, S.P.; Ceder, G. Novel mixed polyanions lithium-ion battery cathode materials predicted by high-throughput ab initio computations. J. Mater. Chem. 2011, 21, 17147–17153. [Google Scholar] [CrossRef]
- Zhu, Z.; Chu, I.H.; Ong, S.P. Li3Y (PS4) 2 and Li5PS4Cl2: New lithium superionic conductors predicted from silver thiophosphates using efficiently tiered ab initio molecular dynamics simulations. Chem. Mater. 2017, 29, 2474–2484. [Google Scholar] [CrossRef]
- Guo, X.; Wang, Z.; Yang, J.; Gong, X.G. Machine-Learning Assisted High-Throughput Discovery of Solid-State Electrolytes for Li-ion Batteries. J. Mater. Chem. A 2024. [Google Scholar] [CrossRef]
- Xi, L.; Zhang, D.; Xu, X.; Wu, Y.; Li, F.; Yao, S.; Zhu, M.; Liu, J. Interface Engineering of All-Solid-State Batteries Based on Inorganic Solid Electrolytes. Chemsuschem 2023, 16, e202202158. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Fan, G.; Zhang, X.; Han, J.; Wang, Y.; Liu, Y.; Jia, L.; Guo, B.; Zhu, C.; He, M. Modeling of an all-solid-state battery with a composite positive electrode. Etransportation 2024, 20, 100315. [Google Scholar] [CrossRef]
- Janek, J.; Zeier, W.G. Challenges in speeding up solid-state battery development. Nat. Energy 2023, 8, 230–240. [Google Scholar] [CrossRef]
- Haftbaradaran, H.; Esmizadeh, S.; Salvadori, A. Competing effects of current density and viscoplastic deformation on the critical conditions for dendrite growth into solid-state lithium battery electrolytes. Int. J. Solids Struct. 2022, 254–255, 111852. [Google Scholar] [CrossRef]
- Di Leo, C.; Rejovitzky, E.; Anand, L. Diffusion-deformation theory for amorphous silicon anodes: The role of plastic deformation on elecrochemical performance. Int. J. Solids Struct. 2015, 67–68, 283–296. [Google Scholar] [CrossRef]
- Fathiannasab, H.; Kashkooli, A.; Li, T.; Zhu, L.; Chen, Z. Three-Dimensional Modeling of All-Solid-State Lithium-Ion Batteries Using Synchrotron Transmission X-ray Microscopy Tomography. J. Electrochem. Soc. 2020, 167, 100558. [Google Scholar] [CrossRef]
- Fathiannasab, H.; Zhu, L.; Chen, Z. Chemo-mechanical modeling of stress evolution in all-solid-state lithium-ion batteries using synchrotron transmission X-ray microscopy tomography. J. Power Sources 2021, 483, 229028. [Google Scholar] [CrossRef]
- Goodenough, J.B.; Kim, Y. Challenges for rechargeable Li batteries. Chem. Mater. 2010, 22, 587–603. [Google Scholar] [CrossRef]
- Adenusi, H.; Chass, G.A.; Passerini, S.; Tian, K.V.; Chen, G. Lithium batteries and the solid electrolyte interphase (SEI)—Progress and outlook. Adv. Energy Mater. 2023, 13, 2203307. [Google Scholar] [CrossRef]
- Koohi-Fayegh, S.; Rosen, M.A. A review of energy storage types, applications and recent developments. J. Energy Storage 2020, 27, 101047. [Google Scholar] [CrossRef]
- Bin Jassar, M.; Michel, C.; Abada, S.; De Bruin, T.; Tant, S.; Nieto-Draghi, C.; Steinmann, S.N. A Perspective on the Molecular Modeling of Electrolyte Decomposition Reactions for Solid Electrolyte Interphase Growth in Lithium-Ion Batteries. Adv. Funct. Mater. 2024, 2313188. [Google Scholar] [CrossRef]
- Diddens, D.; Appiah, W.A.; Mabrouk, Y.; Heuer, A.; Vegge, T.; Bhowmik, A. Modeling the Solid Electrolyte Interphase: Machine Learning as a Game Changer? Adv. Mater. Interfaces 2022, 9, 2101734. [Google Scholar] [CrossRef]
- Landstorfer, M. A Discussion of the Cell Voltage during Discharge of an Intercalation Electrode for Various C-Rates Based on Non-Equilibrium Thermodynamics and Numerical Simulations. J. Electrochem. Soc. 2019, 167, 013518. [Google Scholar] [CrossRef]









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yildiz, E.; Serpelloni, M.; Salvadori, A.; Cabras, L. A Comparative Review of Models for All-Solid-State Li-Ion Batteries. Batteries 2024, 10, 150. https://doi.org/10.3390/batteries10050150
Yildiz E, Serpelloni M, Salvadori A, Cabras L. A Comparative Review of Models for All-Solid-State Li-Ion Batteries. Batteries. 2024; 10(5):150. https://doi.org/10.3390/batteries10050150
Chicago/Turabian StyleYildiz, Erkin, Mattia Serpelloni, Alberto Salvadori, and Luigi Cabras. 2024. "A Comparative Review of Models for All-Solid-State Li-Ion Batteries" Batteries 10, no. 5: 150. https://doi.org/10.3390/batteries10050150








