IMU/Magnetometer-Based Azimuth Estimation with Norm Constraint Filtering
Abstract
:1. Introduction
2. Principle of the Azimuth Solution of a Gyroscope-Aided Magnetometer-Based MWD System
2.1. The Structure of the Gyroscope-Aided Magnetometer-Based MWD System
2.2. Principle of the Typical Geomagnetic Azimuth Solution of a Magnetometer-Based MWD System
2.3. Principle of the Azimuth Solution of a Gyroscope-Aided Magnetometer-Based MWD System
3. Dynamical System Model of Geomagnetic Vector
4. Rotary Norm Constraint Filter Design
4.1. Kalman Filter Design
4.2. Rotary Norm Constraint Filtering Method
5. Experimental Results
5.1. Simulation Experiments
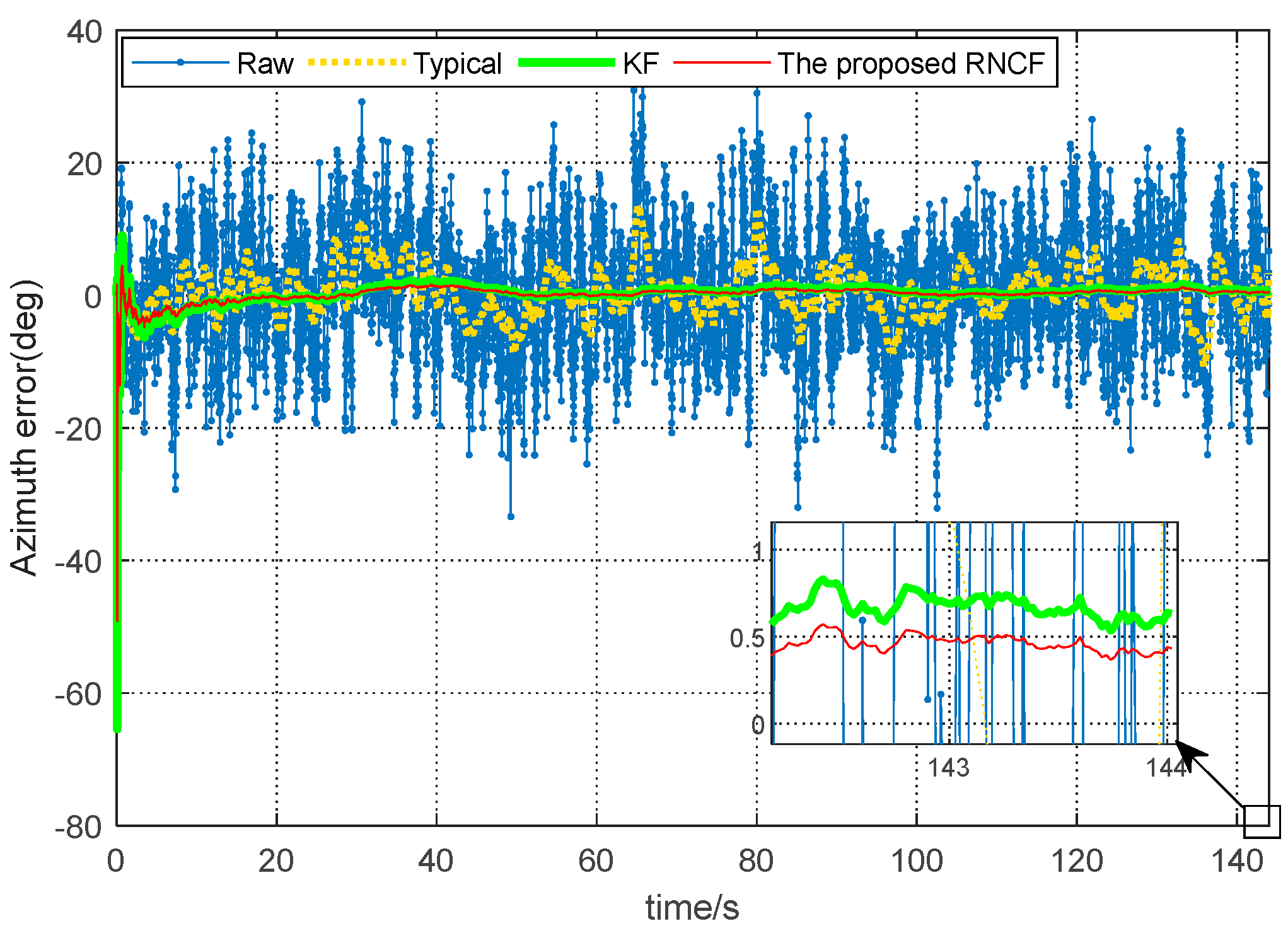
5.2. Actual Drilling Experiment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Qiu, W.; Zeng, Q.; Xu, R.; Liu, J.; Shi, J.; Meng, Q. A multipath mitigation algorithm for GNSS signals based on the steepest descent approach. Satell. Navig. 2022, 3, 14. [Google Scholar] [CrossRef]
- Xue, Q.; Leung, H.; Wang, R.; Liu, B.; Wu, Y. Continuous real-time measurement of drilling trajectory with new state-space models of Kalman filter. IEEE Trans. Instrum. Meas. 2016, 65, 144–154. [Google Scholar] [CrossRef]
- Yang, J.; Cai, J.; Wang, S. Online Compensation of Geomagnetic Measurement Errors While Drilling. IEEE Trans. Instrum. Meas. 2024, 73, 9507109. [Google Scholar] [CrossRef]
- Pecht, E.; Mintchev, M. Modeling of observability during breakin-drilling alignment for horizontal directional drilling. IEEE Trans. Instrum. Meas. 2007, 56, 1946–1954. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, L.; Gao, S.; Lin, T.; Li, X. Vibration noise modeling for measurement while drilling system based on FOGs. Sensors 2017, 17, 2367. [Google Scholar] [CrossRef] [PubMed]
- El-Gizawy, M.; Noureldin, A.; El-Sheimy, N. Performance analysis of tactical grade inertial systems for MWD process. In Proceedings of the IEEE PLANS, San Diego, CA, USA, 25–27 April 2006; pp. 16–22. [Google Scholar]
- Zhang, C.; Lin, T. A long-term performance enhancement method for FOG-based measurement while drilling. Sensors 2016, 16, 1186. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Hu, C.; Xiang, S.; Feng, Z. Magnetic dipole model in the near-field. In Proceedings of the IEEE ICIA, Lijiang, China, 8–10 August 2015; pp. 1085–1089. [Google Scholar]
- Tsatalas, S.; Vergos, D.; Spantideas, S.T.; Kapsalis, N.C.; Kakarakis, S.-D.; Livanos, N.; Hammal, S.; Alifragkis, E.; Bougas, A.; Capsalis, C.; et al. A novel multi-magnetometer facility for on-ground characterization of spacecraft equipment. Measurement 2019, 146, 948–960. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, L. Modeling high-frequency magnetic coupling wired drill pipe channel based on linear simulation. Pet. Drill. Tech. 2019, 47, 120–126. [Google Scholar]
- Saasen, A.; Poedjono, B.; Anesbug, G.O.; Zachman, N. Efficient removal of magnetic contamination from drilling fluids: The effect on directional drilling. J. Energy Resour. Technol. 2021, 143, 103201. [Google Scholar] [CrossRef]
- Wang, Z.; Poscente, M.; Filip, D.; Dimanchev, M.; Mintchev, M.P. Rotary in-drilling alignment using an autonomous MEMS-based inertial measurement unit for measurement-while-drilling processes. IEEE Instrum. Meas. Mag. 2013, 16, 26–34. [Google Scholar] [CrossRef]
- Xu, T.; Wen, D.; Sun, X. Research on azimuth measurement and correction technique with accelerometer and magnetometer. Chin. J. Sci. Instrum. 2009, 30, 2018–2022. [Google Scholar]
- Xue, Q.; Wang, R.; Sun, F.; Huang, L. Continuous measurement-while-drilling utilizing strap-down multi-model surveying system. IEEE Trans. Instrum. Meas. 2014, 63, 650–657. [Google Scholar]
- Liu, Z.; Song, J. A low-cost calibration strategy for measurement-while-drilling system. IEEE Trans. Ind. Electron. 2018, 65, 1080–1090. [Google Scholar]
- Gao, Y.; Cheng, W.; Wang, Y. Multi-source dynamic attitude combination measurement for near-bit drilling tool. Chin. Inert. Technol. 2017, 25, 146–150. [Google Scholar]
- Yang, J.; Yang, C.; Jiang, J. A robust mag/INS-based orientation estimation algorithm for measurement while drilling. IEEE Sens. J. 2017, 17, 7971–7980. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, M.; Lin, T.; Cheng, S. Design of low-cost MIMU /magnetometer integrated MWD system. Chin. Pet. Machinery 2015, 43, 44–48+54. [Google Scholar]
- Sun, K.; Zeng, Q.; Liu, J.; Qiu, W.; Shi, J. Modified attitude factor graph fusion method for unmanned helicopter under atmospheric disturbance. Chin. J. Aeronaut. 2022, 35, 285–297. [Google Scholar] [CrossRef]









| Parameters | Magnetometer (HMC1043) | Accelerometer (MS9010) | Gyroscope (CRG20-02) |
|---|---|---|---|
| Range | ±6 gauss | ±10 g | ±300°/s |
| Resolution | 120 μgauss | 0.1 mg | 0.03125°/s |
| Bias stability | - | <0.25 mg | 4.7°/h |
| Noise | 50 nV/√Hz | 0.140 mg/√Hz | 18 nV/√Hz |
| Working TEMP | −40–125 °C | −55–125 °C | −40–105 °C |
| Magnetic Field (Gauss) | Raw | Typical | KF | The Proposed |
|---|---|---|---|---|
| RMSE (X-axis) | 0.0472 | 0.0222 | 0.0121 | 0.0061 |
| RMSE (Y-axis) | 0.0466 | 0.0195 | 0.0090 | 0.0047 |
| RMSE (Z-axis) | 0.0470 | 0.0211 | 0.0129 | 0.0033 |
| Methods | Raw | Typical | KF | The Proposed |
|---|---|---|---|---|
| Maximum error (°) | 36.62 | 13.50 | 0.96 | 0.63 |
| Minimum error (°) | −33.41 | −10.62 | −0.93 | −0.51 |
| Mean error (°) | −1.59 | −1.53 | 0.79 | 0.54 |
| Steady-state RMSE (°) | 52.17 | 38.64 | 0.89 | 0.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Zeng, Q.; Xiong, Z.; Yang, J. IMU/Magnetometer-Based Azimuth Estimation with Norm Constraint Filtering. Sensors 2024, 24, 2982. https://doi.org/10.3390/s24102982
Yang C, Zeng Q, Xiong Z, Yang J. IMU/Magnetometer-Based Azimuth Estimation with Norm Constraint Filtering. Sensors. 2024; 24(10):2982. https://doi.org/10.3390/s24102982
Chicago/Turabian StyleYang, Chuang, Qinghua Zeng, Zhi Xiong, and Jinxian Yang. 2024. "IMU/Magnetometer-Based Azimuth Estimation with Norm Constraint Filtering" Sensors 24, no. 10: 2982. https://doi.org/10.3390/s24102982





