Muscle Synergy during Wrist Movements Based on Non-Negative Tucker Decomposition
Abstract
:1. Introduction
2. Material and Methods
2.1. Subjects
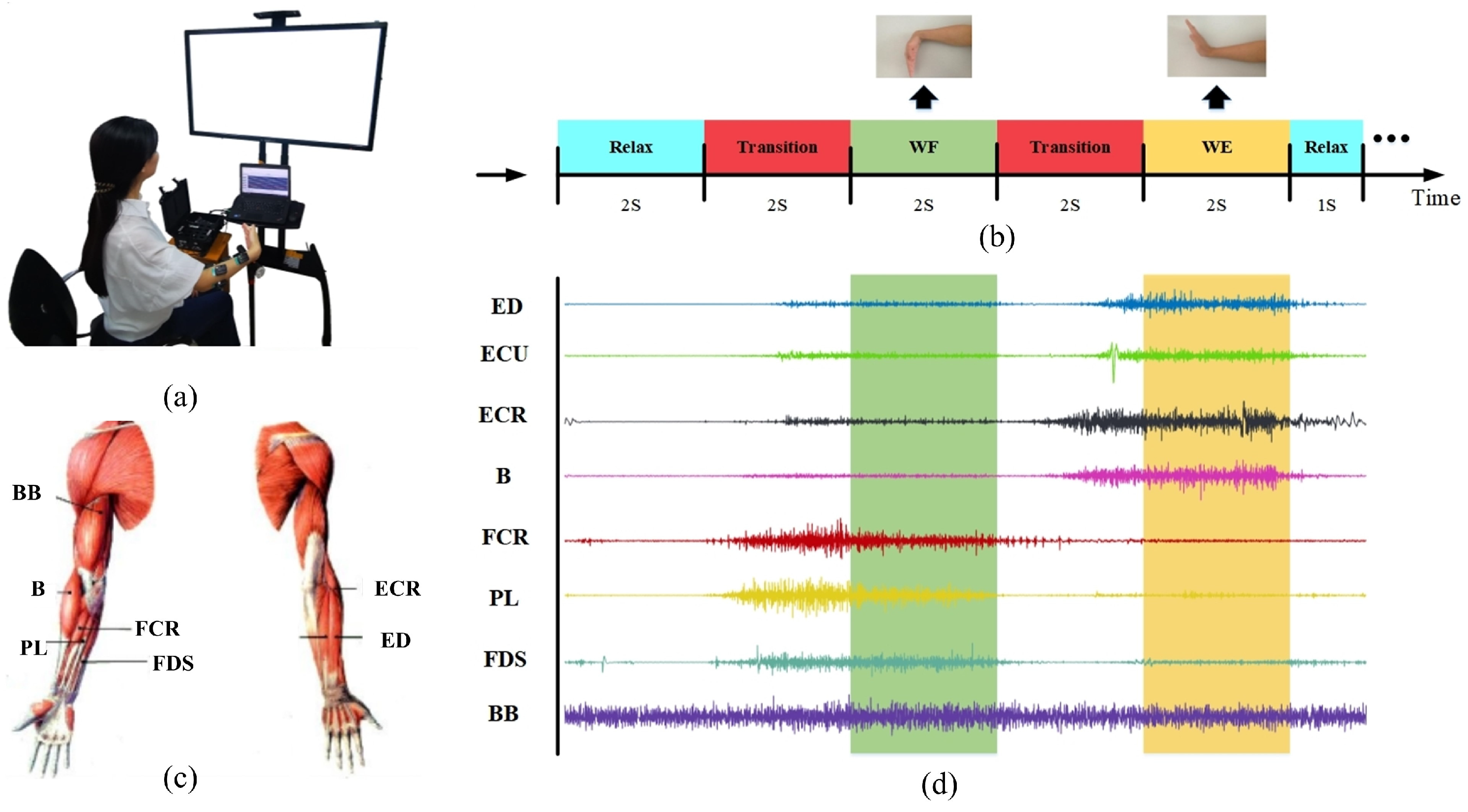
2.2. Experiments and Data Recording
2.2.1. Experiments
2.2.2. Data Recording and Preprocessing
2.3. Method
2.3.1. Non-Negative Matrix Factorization
2.3.2. Non-Negative Tucker Decomposition
2.3.3. Correlation Analysis of Muscle Synergy
3. Result
3.1. Choosing the Optimal Number of Synergies under NTD
3.2. Muscle Synergy Extraction
3.2.1. The Muscle Synergy Estimated by NMF
3.2.2. The Muscle Synergy Estimated by NTD
3.3. Muscle Synergy Similarity between Tasks and Subjects
3.4. Shared Synergy and Specific Synergy
4. Discussion
4.1. Space–Frequency–Time Characteristics of Muscle Synergy
4.2. Shared and Specific Synergy
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- d’Avella, A.; Giese, M.; Ivanenko, Y.P.; Schack, T.; Flash, T. Editorial: Modularity in motor control: From muscle synergies to cognitive action representation. Front. Comput. Neurosci. 2015, 9, 126. [Google Scholar] [CrossRef] [PubMed]
- Gottlieb, G.L. Muscle activation patterns during two types of voluntary single-joint movement. J. Neurophysiol. 1998, 80, 1860–1867. [Google Scholar] [CrossRef] [PubMed]
- d’Avella, A.; Tresch, M. Muscle synergies for motor control. In Handbook of Neural Engineering; Wiley: Hoboken, NJ, USA, 2006; pp. 449–465. [Google Scholar]
- Neptune, R.R.; Clark, D.J.; Kautz, S.A. Modular control of human walking: A simulation study. J. Biomech. 2009, 42, 1282–1287. [Google Scholar] [CrossRef] [PubMed]
- Tigrini, A.; Verdini, F.; Fioretti, S.; Mengarelli, A. On the Decoding of Shoulder Joint Intent of Motion from Transient EMG: Feature Evaluation and Classification. IEEE Trans. Med. Robot. Bionics 2023, 5, 1037–1044. [Google Scholar] [CrossRef]
- Tigrini, A.; Verdini, F.; Scattolini, M.; Barbarossa, F.; Burattini, L.; Morettini, M.; Fioretti, S.; Mengarelli, A. Handwritten digits recognition from sEMG: Electrodes location and feature selection. IEEE Access 2023, 11, 58006–58015. [Google Scholar] [CrossRef]
- Berniker, M.; Jarc, A.; Bizzi, E.; Tresch, M.C. Simplified and effective motor control based on muscle synergies to exploit musculoskeletal dynamics. Proc. Natl. Acad. Sci. USA 2009, 106, 7601–7606. [Google Scholar] [CrossRef]
- Choi, C.; Kim, J. Synergy matrices to extract fluid wrist motion intents via surface electromyography. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2010, 2010, 3511–3514. [Google Scholar] [PubMed]
- Jiang, N.; Rehbaum, H.; Vujaklija, I.; Graimann, B.; Farina, D. Intuitive, Online, Simultaneous, and Proportional Myoelectric Control Over Two Degrees-of-Freedom in Upper Limb Amputees. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 22, 501–510. [Google Scholar] [CrossRef] [PubMed]
- Jolliffe, I.T. Principal Component Analysis. J. Mark. Res. 2002, 87, 513. [Google Scholar]
- Shaharudin, S.; Zanotto, D.; Agrawal, S. Muscle Synergies of Untrained Subjects during 6 min Maximal Rowing on Slides and Fixed Ergometer. J. Sports Sci. Med. 2014, 13, 793–800. [Google Scholar] [PubMed]
- Jutten, C.; Herault, J. Blind separation of sources, part I: An adaptive algorithm based on neuromimetic architecture. Signal Process. 1991, 24, 1–10. [Google Scholar] [CrossRef]
- Comon, P. Independent component analysis, A new concept? Signal Process. 1994, 36, 287–314. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef] [PubMed]
- Ebied, A.; Kinney-Lang, E.; Spyrou, L.; Escudero, J. Evaluation of matrix factorisation approaches for muscle synergy extraction. Med. Eng. Phys. 2018, 57, 51–60. [Google Scholar] [CrossRef] [PubMed]
- Tresch, M.C.; Cheung, V.C.K.; D’Avella, A. Matrix factorization algorithms for the identification of muscle synergies: Evaluation on simulated and experimental data sets. J. Neurophysiol. 2006, 95, 2199–2212. [Google Scholar] [CrossRef] [PubMed]
- De Marchis, C.; Severini, G.; Castronovo, A.M.; Schmid, M.; Conforto, S. Intermuscular coherence contributions in synergistic muscles during pedaling. Exp. Brain Res. 2015, 233, 1907–1919. [Google Scholar] [CrossRef] [PubMed]
- Haghpanah, S.A.; Farahmand, F.; Zohoor, H. Modular neuromuscular control of human locomotion by central pattern generator. J. Biomech. 2017, 53, 154–162. [Google Scholar] [CrossRef] [PubMed]
- Tang, L.; Chen, X.; Cao, S.; Wu, D.; Zhao, G.; Zhang, X. Assessment of Upper Limb Motor Dysfunction for Children with Cerebral Palsy Based on Muscle Synergy Analysis. Front. Hum. Neurosci. 2017, 11, 130. [Google Scholar] [CrossRef] [PubMed]
- D’Avella, A.; Bizzi, E. Shared and specific muscle synergies in natural motor behaviors. Proc. Natl. Acad. Sci. USA 2005, 102, 3076–3081. [Google Scholar] [CrossRef] [PubMed]
- Gagné, M.; Schneider, C. Dynamic influence of wrist flexion and extension on the intracortical inhibition of the first dorsal interosseus muscle during precision grip. Brain Res. 2008, 1195, 77–88. [Google Scholar] [CrossRef] [PubMed]
- Kolda, T.G.; Bader, B.W. Tensor Decompositions and Applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Cong, F.; Lin, Q.H.; Kuang, L.D.; Gong, X.F.; Astikainen, P.; Ristaniemi, T. Tensor decomposition of EEG signals: A brief review. J. Neurosci. Methods 2015, 248, 59–69. [Google Scholar] [CrossRef] [PubMed]
- Mocks, J. Topographic components model for event-related potentials and some biophysical considerations. IEEE Trans. Biomed. Eng. 1988, 35, 482–484. [Google Scholar] [CrossRef]
- Sidiropoulos, N.D.; De Lathauwer, L.; Fu, X.; Huang, K.; Papalexakis, E.; Faloutsos, C. Tensor Decomposition for Signal Processing and Machine Learning. IEEE Trans. Signal Process. 2017, 65, 3551–3582. [Google Scholar] [CrossRef]
- Yang, H.; He, G.; Dong, Y. Nonnegative Tensor Decomposition and It’s Applications in Image Processing. In Proceedings of the 2008 International Conference on Computer Science and Information Technology, Singapore, 29 August–2 September 2008; pp. 212–217. [Google Scholar]
- Ebied, A.; Kinney-Lang, E.; Escudero, J. Consistency of Muscle Synergies Extracted via Higher-Order Tensor Decomposition Towards Myoelectric Control. In Proceedings of the 2019 9th International IEEE/EMBS Conference on Neural Engineering (NER), San Francisco, CA, USA, 20–23 March 2019; IEEE: New York, NY, USA, 2019. [Google Scholar]
- Ebied, A.; Kinney-Lang, E.; Spyrou, L.; Escudero, J. Muscle Activity Analysis Using Higher-Order Tensor Decomposition: Application to Muscle Synergy Extraction. IEEE Access 2019, 7, 27257–27271. [Google Scholar] [CrossRef]
- Kendall, F.P.; McCreary, E.K.; Provance, P.G.; Provance, M.M.; Romani, W.A. Muscles: Testing and Function, with Posture and Pain; Lippincott Williams & Wilkins: Baltimore, MD, USA, 2005; Volume 5. [Google Scholar]
- Stephen, M.; Stephen, M. EMG-EMG Coherence Analysis of Elbow and Shoulder Muscles. Master’s Thesis, Washington University in St. Louis, St. Louis, MO, USA, 2013. [Google Scholar]
- Kang, K. Wrist Movement Classification Using Multi-Channel Surface EMG. Master’s Thesis, San Diego State University, San Diego, CA, USA, 2016. [Google Scholar]
- Rau, D.K. Development of recommendations for SEMG sensors and sensor placement procedures. J. Electromyogr. Kinesiol. 2000, 10, 361–374. [Google Scholar]
- Ranaldi, S.; De Marchis, C.; Severini, G.; Conforto, S. An Objective, Information-Based Approach for Selecting the Number of Muscle Synergies to be Extracted via Non-Negative Matrix Factorization. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 2676–2683. [Google Scholar] [CrossRef] [PubMed]
- Soomro, M.H.; Conforto, S.; Giunta, G.; Ranaldi, S.; De Marchis, C. Comparison of Initialization Techniques for the Accurate Extraction of Muscle Synergies from Myoelectric Signals via Nonnegative Matrix Factorization. Appl. Bionics Biomech. 2018, 2018, 3629347. [Google Scholar] [CrossRef]
- Kattla, S.; Lowery, M.M. Fatigue related changes in electromyographic coherence between synergistic hand muscles. Exp. Brain Res. 2010, 202, 89–99. [Google Scholar] [CrossRef] [PubMed]
- Clark, D.J.; Ting, L.H.; Zajac, F.E.; Neptune, R.R.; Kautz, S.A.; Bruton, M.; O’dwyer, N.; Allen, J.L.; Franz, J.R.; Sawers, A.; et al. Merging of healthy motor modules predicts reduced locomotor performance and muscle coordination complexity post-stroke. J. Neurophysiol. 2010, 103, 844. [Google Scholar] [CrossRef] [PubMed]
- Steele, K.M.; Tresch, M.C.; Perreault, E.J. Perreault, The number and choice of muscles impact the results of muscle synergy analyses. Front. Comput. Neurosci. 2013, 7, 105. [Google Scholar] [CrossRef] [PubMed]
- Boonstra, T.W.; Danna-Dos-Santos, A.; Xie, H.-B.; Roerdink, M.; Stins, J.F.; Breakspear, M. Muscle networks: Connectivity analysis of EMG activity during postural control. Sci. Rep. 2015, 5, 17830. [Google Scholar] [CrossRef] [PubMed]
- Mallat, S.G. A Wavelet Tour of Signal Processing; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Chen, X.; Dong, X.; Feng, Y.; Jiao, Y.; Yu, J.; Song, Y.; Li, X.; Zhang, L.; Hou, P.; Xie, P. Muscle activation patterns and muscle synergies reflect different modes of coordination during upper extremity movement. Front. Hum. Neurosci. 2023, 16, 912440. [Google Scholar] [CrossRef] [PubMed]
- Xie, P.; Chang, Q.; Zhang, Y.; Dong, X.; Yu, J.; Chen, X. Estimation of time-frequency muscle synergy in wrist movements. Entropy 2022, 24, 707. [Google Scholar] [CrossRef] [PubMed]
- Baker, S.N.; Olivier, E.; Lemon, R.N. Coherent oscillations in monkey motor cortex and hand muscle EMG show task-dependent modulation. J. Physiol. 2004, 501, 225–241. [Google Scholar] [CrossRef] [PubMed]
- Jung, C.Y.; Park, J.S.; Lim, Y.; Kim, Y.B.; Park, K.K.; Moon, J.H.; Song, J.H.; Lee, S. Estimating fatigue level of femoral and gastrocemius muscles based on surface electromyography in time and frequency domain. J. Mech. Med. Biol. 2018, 18, 1850042. [Google Scholar] [CrossRef]
- Tresch, M.C.; Saltiel, P.; Bizzi, E. The construction of movement by the spinal cord. Nat. Neurosci. 1999, 2, 162–167. [Google Scholar] [CrossRef]
- Norton, J.A.; Wood, D.E.; Marsden, J.F.; Day, B.L. Spinally generated electromyographic oscillations and spasms in a low-thoracic complete paraplegic. Mov. Disord. Off. J. Mov. Disord. Soc. 2003, 18, 101–106. [Google Scholar] [CrossRef] [PubMed]
- Qiu, Q.; Cao, L.; Hao, D.; Yang, L.; Hillstrom, R.; Zheng, D. Muscle Extremely Low Frequency Magnetic Stimulation Eliminates the Effect of Fatigue on EEG-EMG Coherence during the Lateral Raise Task: A Pilot Quantitative Investigation. Biomed Res. Int. 2018, 2018, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Ivanenko, Y.P.; Poppele, R.E.; Lacquaniti, F. Five basic muscle activation patterns account for muscle activity during human locomotion. J. Physiol. 2010, 556 Pt 1, 267–282. [Google Scholar] [CrossRef]
- Fautrelle, L.; Ballay, Y.; Bonnetblanc, F. Muscular synergies during motor corrections: Investigation of the latencies of muscle activities. Behav. Brain Res. 2010, 214, 428–436. [Google Scholar] [CrossRef] [PubMed]





| Synergy Module Subjects | W(1) | W(2) | W(3) |
|---|---|---|---|
| S1 | PL FDS BB | ECR FCR | FCR BB |
| S2 | BB | FCR FDS | ECRFDS BB |
| S3 | FDS BB | ECR FCRPL | FCR BB |
| S4 | PL FDS | FCR PL | ECU ECR B |
| S5 | FDS | ECR B | FCR PL BB |
| S6 | PL | BB | ECR FCRPL |
| S7 | FCR PL | PL FDS | ECR |
| S8 | ED ECU FDS | B FCR PL | BB |
| S9 | FCR PL | FDS BB | PL BB |
| S10 | FDS BB | ED FCR | FCR PLFDS |
| Synergy Module Subjects | W(1) | W(2) | W(3) |
|---|---|---|---|
| S1 | BB | ECR PL | ED ECR B |
| S2 | ECU ECR B | BB | ED ECUECR |
| S3 | ECU | BB | FDS PL |
| S4 | ED ECU ECRB | ECU | PL BB |
| S5 | ED ECR B | BB | B FDS |
| S6 | ECU ECR B | BB | ECU B FDS |
| S7 | ECR B | ED BB | ECR B |
| S8 | ED B | ECR BB | BB |
| S9 | ECR B | BB | ECU ECR B |
| S10 | ECR B | BB | ECR B |
| Muscle Synergy Module | WE-W(1) | WE-W(2) | WE-W(3) |
|---|---|---|---|
| WF-W(1) | 0.571 | 0.476 | −0.762 |
| WF-W(2) | 0.191 | −0.071 | 0.167 |
| WF-W(3) | 0.333 | 0.7619 | −0.286 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Feng, Y.; Chang, Q.; Yu, J.; Chen, J.; Xie, P. Muscle Synergy during Wrist Movements Based on Non-Negative Tucker Decomposition. Sensors 2024, 24, 3225. https://doi.org/10.3390/s24103225
Chen X, Feng Y, Chang Q, Yu J, Chen J, Xie P. Muscle Synergy during Wrist Movements Based on Non-Negative Tucker Decomposition. Sensors. 2024; 24(10):3225. https://doi.org/10.3390/s24103225
Chicago/Turabian StyleChen, Xiaoling, Yange Feng, Qingya Chang, Jinxu Yu, Jie Chen, and Ping Xie. 2024. "Muscle Synergy during Wrist Movements Based on Non-Negative Tucker Decomposition" Sensors 24, no. 10: 3225. https://doi.org/10.3390/s24103225





