Enhancement of Heat Transfer in a Microchannel via Passive and Active Control of a Jet Issued from the Circular Cylinder
Abstract
:1. Introduction
2. Physical Model and Problem Statement
3. Mathematical Formulation and Numerical Procedure
3.1. Governing Equations and Numerical Method
3.2. Boundary Conditions
3.3. Numerical Verification and Grid Independence
4. Results and Discussion
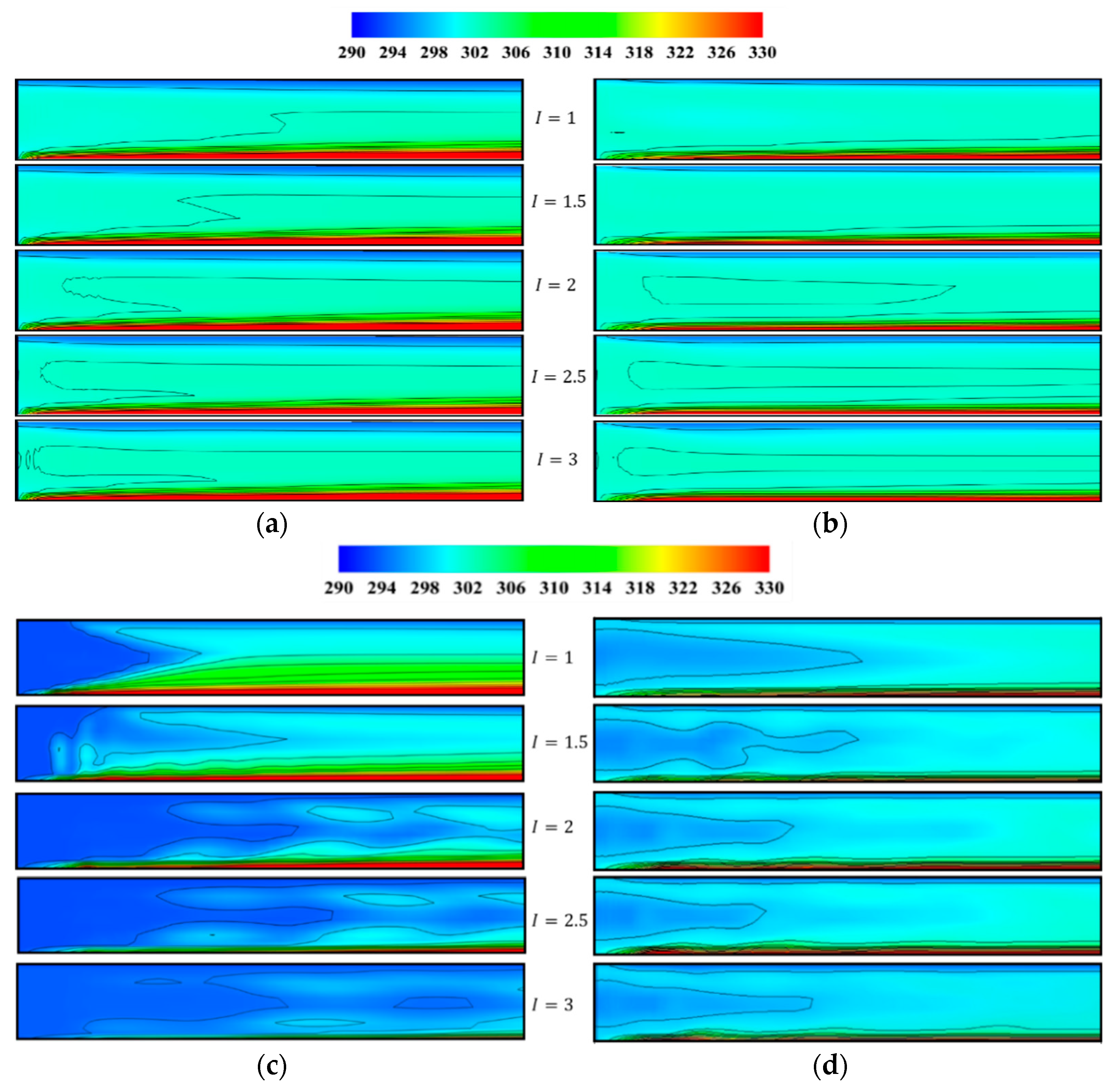
4.1. Effect of the Injection Ratio
4.1.1. Heat Transfer Performance
4.1.2. Physical Mechanisms of Flow and Heat Transfer
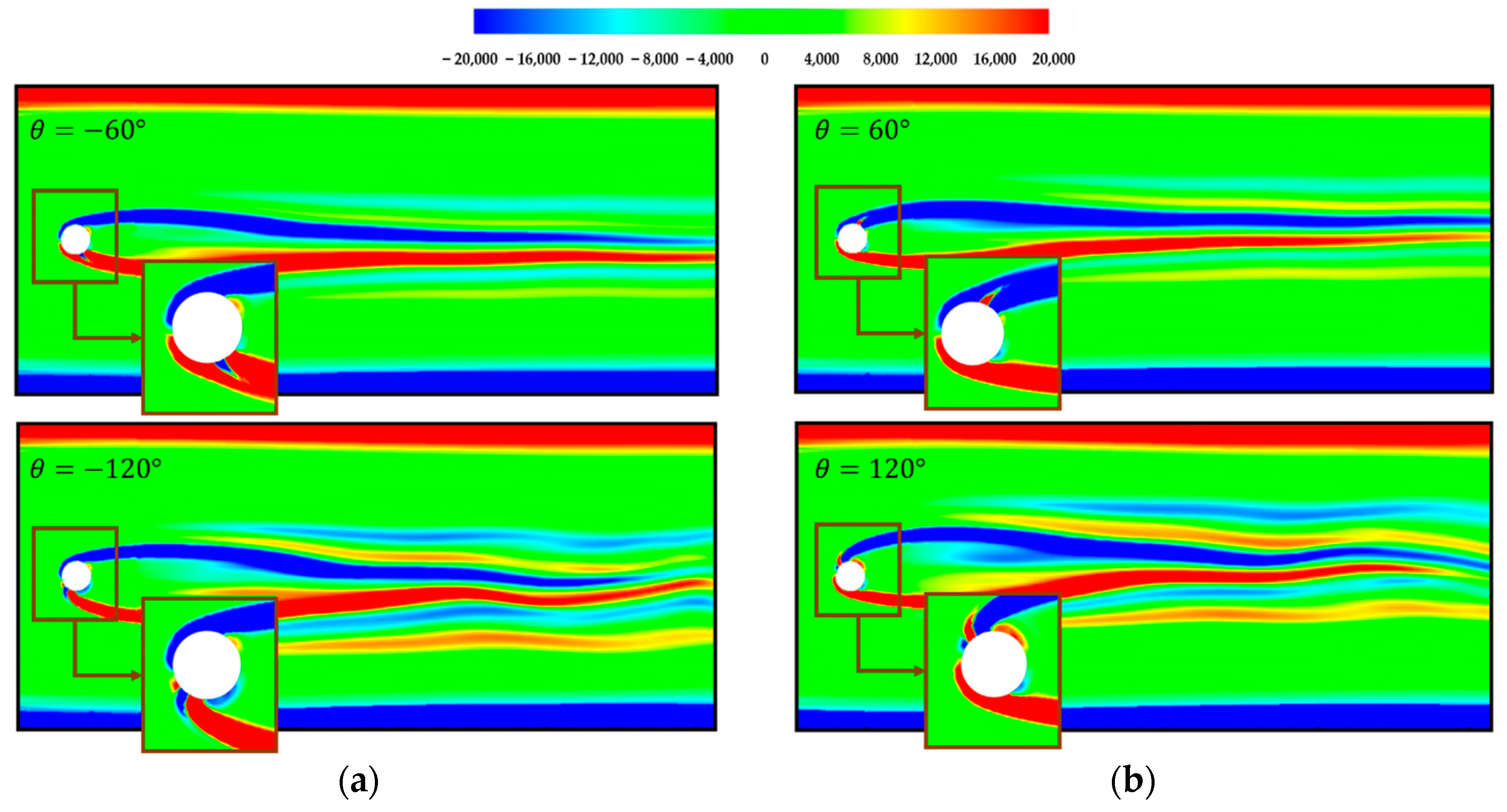
4.2. Effect of the Jet Angles
4.2.1. Heat Transfer Performance
4.2.2. Physical Mechanisms of Flow and Heat Transfer
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Deng, H.; Teng, J.; Zhu, M.; Qiang, X.; Lu, S.; Jiang, Y. Overall cooling performance evaluation for film cooling with different winglet pairs vortex generators. Appl. Therm. Eng. 2022, 201, 117731. [Google Scholar] [CrossRef]
- Babar, H.; Ali, H.M. Towards hybrid nanofluids: Preparation, thermophysical properties, applications, and challenges. J. Mol. Liq. 2019, 281, 598–633. [Google Scholar] [CrossRef]
- Wu, F.; Li, L.; Wang, J.; Fan, X.; Du, C. Numerical investigations on flow and heat transfer of swirl and impingement composite cooling structures of turbine blade leading edge. Int. J. Heat Mass Transf. 2019, 144, 118625. [Google Scholar] [CrossRef]
- Tuckerman, D.B.; Pease, R.F.W. High-Performance Heat Sinking for VLSI. IEEE Electron Device Lett. 1981, 2, 126–129. [Google Scholar] [CrossRef]
- Dadvand, A.; Hosseini, S.; Aghebatandish, S.; Khoo, B.C. Enhancement of heat and mass transfer in a microchannel via passive oscillation of a flexible vortex generator. Chem. Eng. Sci. 2019, 207, 556–580. [Google Scholar] [CrossRef]
- Ismael, M.A. Forced convection in partially compliant channel with two alternated baffles. Int. J. Heat Mass Transf. 2019, 142, 118455. [Google Scholar] [CrossRef]
- Ebaika, J.A.; Shuja, S.Z.; Yilbas, B.S.; Al-Qahtani, H. Microchannel flow and heat transfer enhancement via ribs arrangements. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2022, 236, 668–684. [Google Scholar] [CrossRef]
- Kakac, S.; Shah, R.K.; Aung, W. Handbook of Single-Phase Convective Heat Transfer; Wiley-Interscience: New York, NY, USA, 1987; p. 408. [Google Scholar]
- Rahnama, M.; Moghaddam, H.H. Numerical investigation of convective heat transfer in unsteady laminar flow over a square cylinder in a channel. Heat Transf. Eng. 2005, 26, 21–29. [Google Scholar] [CrossRef]
- He, J.; Deng, Q.; Xiao, K.; Feng, Z. Impingement Heat Transfer Enhancement in Crossflow by V-Shaped Protrusion Vortex Generator. Heat Transf. Eng. 2022, 1–26. [Google Scholar] [CrossRef]
- Turki, S.; Abbassi, H.; Nasrallah, S.B. Two-dimensional laminar fluid flow and heat transfer in a channel with a built-in heated square cylinder. Int. J. Therm. Sci. 2003, 42, 1105–1113. [Google Scholar] [CrossRef]
- Abbassi, H.; Turki, S.; Nasrallah, S.B. Mixed convection in a plane channel with a built-in triangular prism. Numer. Heat Transf. Part A Appl. 2001, 39, 307–320. [Google Scholar]
- Nitin, S.; Chhabra, R.P. Non-isothermal flow of a power law fluid past a rectangular obstacle (of aspect ratio 1 × 2) in a channel: Drag and heat transfer. Int. J. Eng. Sci. 2005, 43, 707–720. [Google Scholar] [CrossRef]
- Abbassi, H.; Turki, S.; Nasrallah, S.B. Numerical investigation of forced convection in a lane channel with a built-in triangular prism. Int. J. Therm. Sci. 2001, 40, 649–658. [Google Scholar] [CrossRef]
- Meis, M.; Varas, F.; Velázquez, A.; Vega, J.M. Heat transfer enhancement in micro-channels caused by vortex promoters. Int. J. Heat Mass Transf. 2010, 53, 29–40. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Liu, J.; Pan, Z. Enhancement of heat transfer and mixing with two side-by-side freely rotatable cylinders in microchannel. Int. J. Heat Mass Transf. 2022, 189, 122717. [Google Scholar] [CrossRef]
- Lin, Y.; Luo, Y.; Li, W.; Minkowycz, W.J. Enhancement of flow boiling heat transfer in microchannel using micro-fin and micro-cavity surfaces. Int. J. Heat Mass Transf. 2021, 179, 121739. [Google Scholar] [CrossRef]
- Amini, Y.; Akhavan, S.; Izadpanah, E. A numerical investigation on the heat transfer characteristics of nanofluid flow in a three-dimensional microchannel with harmonic rotating vortex generators. J. Therm. Anal. Calorim. 2020, 139, 755–764. [Google Scholar] [CrossRef]
- Shamsoddini, L.M. Fluid flow and heat transfer in microchannel with and without porous medium under constant heat flux. Sadhana 2022, 47, 1–12. [Google Scholar] [CrossRef]
- Armellini, A.; Casarsa, L.; Giannattasio, P. Separated flow structures around a cylindrical obstacle in a narrow channel. Exp. Therm. Fluid Sci. 2009, 33, 604–619. [Google Scholar] [CrossRef]
- Sahin, B.; Ozturk, N.A.; Gurlek, C. Horseshoe vortex studies in the passage of a model plate-fin-and-tube heat exchanger. Int. J. Heat Fluid Flow 2008, 29, 340–351. [Google Scholar] [CrossRef]
- Reddy, K.S.; Lokeswaran, S.; Agarwal, P.; Mallick, T.K. Numerical investigation of micro-channel based active module cooling for solar CPV system. Energy Procedia 2014, 54, 400–416. [Google Scholar] [CrossRef]
- Ren, R.; Zhao, Y.; Diao, Y.; Liang, L.; Jing, H. Active air cooling thermal management system based on U-shaped micro heat pipe array for lithium-ion battery. J. Power Sources 2021, 507, 230314. [Google Scholar] [CrossRef]
- Jalali, E.; Ali Akbari, O.; Sarafraz, M.M.; Abbas, T.; Safaei, M.R. Heat transfer of oil/MWCNT nanofluid jet injection inside a rectangular microchannel. Symmetry 2019, 11, 757. [Google Scholar] [CrossRef] [Green Version]
- Wong, K.C. Numerical investigation of a crossflow jet in a rectangular microchannel. Appl. Mech. Mater. 2013, 284, 849–853. [Google Scholar] [CrossRef]
- Benayad, Z.; Laouedj, S.; Filali, A. Numerical investigation on the cooling of electronics components with synthetic multi-jets and non-sinusoidal bi-periodic forcing functions. Energy Rep. 2020, 6, 1–9. [Google Scholar] [CrossRef]
- Zunaid, M.; Cho, H.M.; Husain, A.; Jindal, A.; Kumar, R.; Chauhan, B.S. Computational analysis of liquid jet impingement micro-channel cooling. Mater. Today Proc. 2018, 5, 27877–27883. [Google Scholar] [CrossRef]
- Paolillo, G.; Greco, C.S.; Cardone, G. Impingement heat transfer of quadruple synthetic jets. Int. J. Heat Mass Transf. 2019, 135, 1192–1206. [Google Scholar] [CrossRef]
- Shi, X.; Jiang, G.; Wei, B.; Kong, X. Research on geometrical parameters effect of fan nozzle jet performance based on orthogonal experiment. J. Eng. 2019, 2019, 119–126. [Google Scholar] [CrossRef]
- Karthikeyan, S.; Senthilkumar, S.; Kannan, B.T.; Chandrasekhar, U. Numerical analysis on effect of jet injection on vortex shedding for flow over a circular cylinder. Arab. J. Sci. Eng. 2019, 44, 1475–1488. [Google Scholar] [CrossRef]
- Jung, J. Physics of Active Flow Control Around a Pillar at the Micro Scale. Ph.D. Thesis, Rensselaer Polytechnic Institute Troy, New York, NY, USA, 2011. Umi Dissertation Publishing: 2012. [Google Scholar]
- Jung, J.; Kuo, C.J.; Peles, Y.; Amitay, M. The flow field around a micropillar confined in a microchannel. Int. J. Heat Fluid Flow 2012, 36, 118–132. [Google Scholar] [CrossRef]
- Ming, T.; Cai, C.; Yang, W.; Shen, W.; Gan, T. Optimization of dimples in microchannel heat sink with impinging jets—Part A: Mathematical model and the influence of dimple radius. J. Therm. Sci. 2018, 27, 195–202. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson Education: Harlow, UK; New York, NY, USA, 2010. [Google Scholar]
- Feng, L.H.; Wang, J.J. Circular cylinder vortex-synchronization control with a synthetic jet positioned at the rear stagnation point. J. Fluid Mech. 2010, 662, 232–259. [Google Scholar] [CrossRef]
- Feng, L.H.; Wang, J.J.; Pan, C. Effect of novel synthetic jet on wake vortex shedding modes of a circular cylinder. J. Fluids Struct. 2010, 26, 900–917. [Google Scholar] [CrossRef]
- Mishra, A.; De, A. Suppression of vortex shedding using a slit through the circular cylinder at low Reynolds number. Eur. J. Mech.-B/Fluids 2021, 89, 349–366. [Google Scholar] [CrossRef]
- Fu, W.S.; Lai, Y.C.; Li, C.G. Estimation of turbulent natural convection in horizontal parallel plates by the Q criterion. Int. Commun. Heat Mass Transf. 2013, 45, 41–46. [Google Scholar] [CrossRef]
- Sumner, D. Flow above the free end of a surface-mounted finite-height circular cylinder: A review. J. Fluids Struct. 2013, 43, 41–63. [Google Scholar] [CrossRef]

















| Grid Size | Coarse | Medium | Fine |
|---|---|---|---|
| Number of nodes Nusselt number (Nu) | 204,732 | 430,170 | 783,496 |
| 3.85 | 3.93 | 3.93 |
| Jet Angles | Thermal Efficiency | Percentage |
|---|---|---|
| 90 | 1.306 | 20.8 |
| 105 | 1.335 | 23.5 |
| 120 | 1.227 | 13.5 |
| 135 | 1.157 | 7.0 |
| 150 | 1.184 | 9.5 |
| 165 | 1.124 | 4.0 |
| 180 | 1.081 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, Z.; Kong, X.; Chen, J. Enhancement of Heat Transfer in a Microchannel via Passive and Active Control of a Jet Issued from the Circular Cylinder. Energies 2022, 15, 8287. https://doi.org/10.3390/en15218287
Xin Z, Kong X, Chen J. Enhancement of Heat Transfer in a Microchannel via Passive and Active Control of a Jet Issued from the Circular Cylinder. Energies. 2022; 15(21):8287. https://doi.org/10.3390/en15218287
Chicago/Turabian StyleXin, Zhiqiang, Xiangyu Kong, and Jing Chen. 2022. "Enhancement of Heat Transfer in a Microchannel via Passive and Active Control of a Jet Issued from the Circular Cylinder" Energies 15, no. 21: 8287. https://doi.org/10.3390/en15218287




