Modelling the Melting Kinetics of Polyetheretherketone Depending on Thermal History: Application to Additive Manufacturing
Abstract
:1. Introduction
2. Experimental Section
2.1. Equipment
2.2. Material
2.3. Methods
- (1)
- Erasing the thermal history at a temperature TMAX of 380 °C above the melting temperature to be sure to melt all of the crystals in the sample. This is followed by a cooling step up to the isothermal crystallization temperature TISO at a cooling rate QQUENCH of 2000 K.s−1 to remain in a fully amorphous state.
- (2)
- Crystallization step: Holding at the isotherm temperature TISO for a defined time ti.
- (3)
- Cooling below the glass transition temperature to TMIN at QQUENCH to stop the crystallization.
- (4)
- Analysis step: Heating above the melting temperature at a defined rate QMEASURE of 500 K.s−1 to analyse the amount of material that crystallized in step (3) by measuring the melting enthalpy.
3. Modelling Section
3.1. Crystallization Model
3.1.1. Isothermal Crystallization
3.1.2. Non-Isothermal Crystallization
3.2. Melting Model
3.2.1. Melting after Isothermal Crystallization
3.2.2. Melting Temperature Dependency
3.2.3. Melting after Non-Isothermal Cooling
4. Results and Discussion
4.1. Isothermal Crystallization Kinetics
4.2. Non-Isothermal Crystallization Kinetics
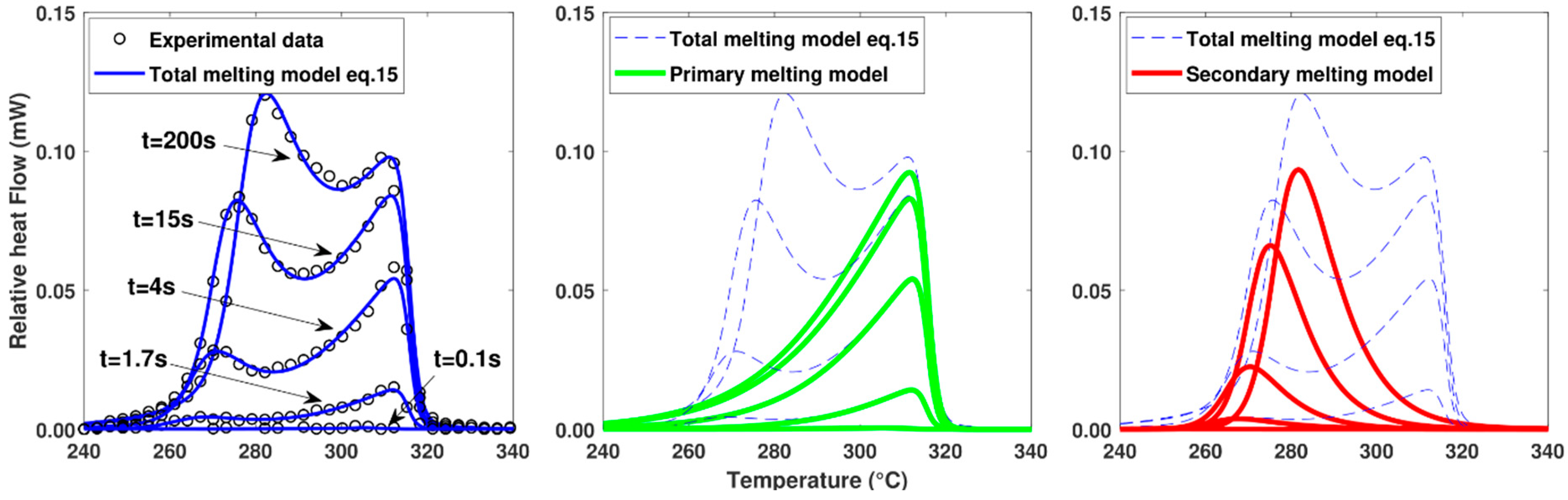
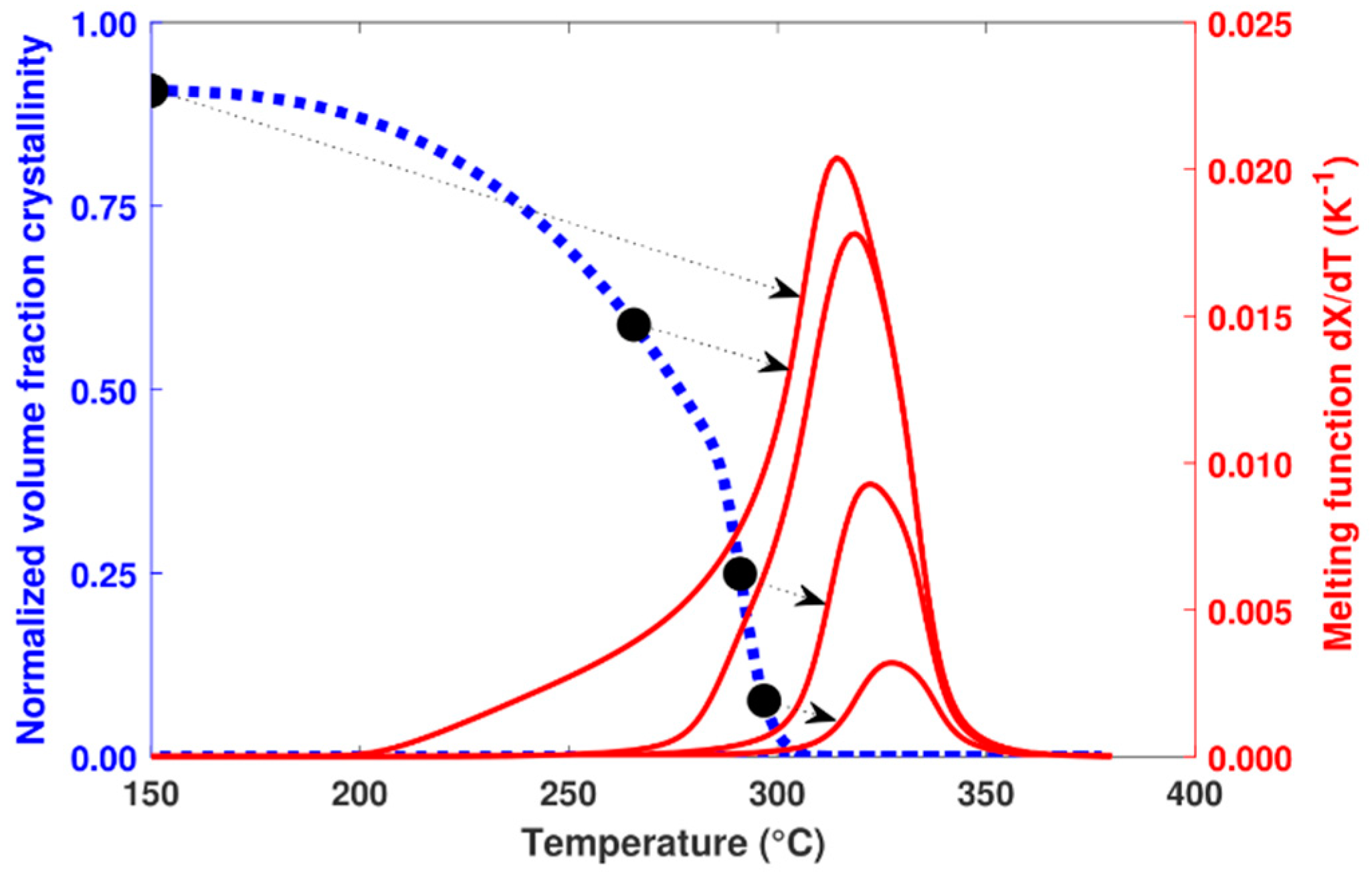
4.3. Melting Kinetics
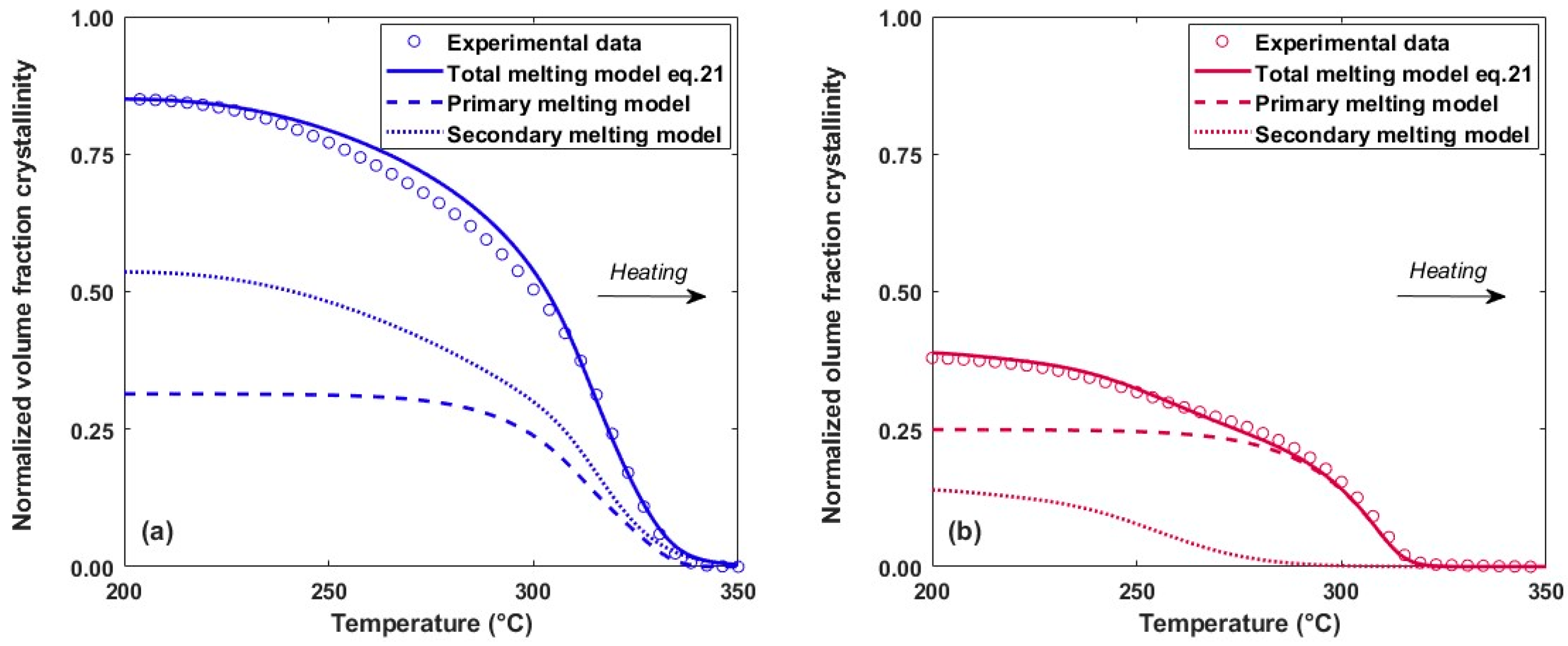
4.4. Model Applied on Additive Manufacturing Process
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Yin, J.; Lu, C.; Fu, J.; Huang, Y.; Zheng, Y. Interfacial bonding during multi-material fused deposition modeling (FDM) process due to inter-molecular diffusion. Mater. Des. 2018, 150, 104–112. [Google Scholar] [CrossRef]
- Lepoivre, A.; Boyard, N.; Levy, A.; Sobotka, V. Heat Transfer and Adhesion Study for the FFF Additive Manufacturing Process. Procedia Manuf. 2020, 47, 948–955. [Google Scholar] [CrossRef]
- Wool, R.P. Polymer Interfaces: Structure and Strength; Carl Hanser: Munich, Germany, 1995. [Google Scholar]
- Martineau, L.; Chabert, F.; Boniface, B.; Bernhart, G. Effect of interfacial crystalline growth on autohesion of PEEK. Int. J. Adhes. Adhes. 2019, 89, 82–87. [Google Scholar] [CrossRef]
- Verma, R.; Marand, H.; Hsiao, B. Morphological Changes during Secondary Crystallization and Subsequent Melting in Poly(ether ether ketone) as Studied by Real Time Small Angle X-ray Scattering. Macromolecules 1996, 29, 7767–7775. [Google Scholar] [CrossRef]
- Hsiao, B.S.; Gardner, K.H.; Wu, D.Q.; Chu, B. Time-resolved X-ray study of poly(aryl ether ether ketone) crystallization and melting behavior: 1. Crystallization. Polymer 1993, 34, 3986–3995. [Google Scholar] [CrossRef]
- Hillier, I.H. Modified avrami equation for the bulk crystallization kinetics of spherulitic polymers. J. Polym. Sci. A Gen. Pap. 1965, 3, 3067–3078. [Google Scholar] [CrossRef]
- Velisaris, C.N.; Seferis, J.C. Crystallization kinetics of polyetheretherketone (peek) matrices. Polym. Eng. Sci. 1986, 26, 1574–1581. [Google Scholar] [CrossRef]
- Tardif, X.; Pignon, B.; Boyard, N.; Schmelzer, J.W.P.; Sobotka, V.; Delaunay, D.; Schick, C. Experimental study of crystallization of PolyEtherEtherKetone (PEEK) over a large temperature range using a nano-calorimeter. Polym. Test. 2014, 36, 10–19. [Google Scholar] [CrossRef]
- Baumard, T.; Rassy, E.E.; Boyard, N.; Corre, S.L.; Bailleul, J.-L.; Bikard, J.; Trouillet-Fonti, L. A stepwise method for the characterization of non-isothermal crystallization kinetics of poly(ether ether ketone) at processing-relevant cooling rates. In Proceedings of the 20th European Conference on Composite Materials, Lausanne, Switzerland, 26–30 June 2022. [Google Scholar]
- Kelly, C.A.; Jenkins, M.J. Modeling the crystallization kinetics of polymers displaying high levels of secondary crystallization. Polym. J. 2022, 54, 249–257. [Google Scholar] [CrossRef]
- Marand, H.; Huang, Z. Isothermal Lamellar Thickening in Linear Polyethylene: Correlation between the Evolution of the Degree of Crystallinity and the Melting Temperature. Macromolecules 2004, 37, 6492–6497. [Google Scholar] [CrossRef]
- Hoffman, J.D.; Weeks, J.J. Melting process and the equilibrium melting temperature of polychlorotrifluoroethylene. J. Res. Natl. Bur. Stand. A 1962, 66A, 13–28. [Google Scholar] [CrossRef]
- Greco, A.; Maffezzoli, A. Statistical and kinetic approaches for linear low-density polyethylene melting modeling. J. Appl. Polym. Sci. 2003, 89, 289–295. [Google Scholar] [CrossRef]
- Toda, A.; Tomita, C.; Hikosaka, M.; Saruyama, Y. Melting of polymer crystals observed by temperature modulated d.s.c. and its kinetic modelling. Polymer 1998, 39, 5093–5104. [Google Scholar] [CrossRef]
- Tierney, J.J.; Gillespie, J.W., Jr. Crystallization kinetics behavior of PEEK based composites exposed to high heating and cooling rates. Compos. Part A Appl. Sci. Manuf. 2004, 35, 547–558. [Google Scholar] [CrossRef]
- Furushima, Y.; Schick, C.; Toda, A. Crystallization, recrystallization, and melting of polymer crystals on heating and cooling examined with fast scanning calorimetry. Polym. Cryst. 2018, 1, e10005. [Google Scholar] [CrossRef]
- Toda, A.; Androsch, R.; Schick, C. Insights into polymer crystallization and melting from fast scanning chip calorimetry. Polymer 2016, 91, 239–263. [Google Scholar] [CrossRef]
- Lattimer, M.P.; Hobbs, J.K.; Hill, M.J.; Barham, P.J. On the origin of the multiple endotherms in PEEK. Polymer 1992, 33, 3971–3973. [Google Scholar] [CrossRef]
- Pérez-Martín, H.; Mackenzie, P.; Baidak, A.; Brádaigh, C.M.Ó.; Ray, D. Crystallisation behavior and morphological studies of PEKK and carbon fibre/PEKK composites. Compos. Part A Appl. Sci. Manuf. 2022, 159, 106992. [Google Scholar] [CrossRef]
- Bas, C.; Battesti, P.; Albérola, N.D. Crystallization and melting behaviors of poly(aryletheretherketone) (PEEK) on origin of double melting peaks. J. Appl. Polym. Sci. 1994, 53, 1745–1757. [Google Scholar] [CrossRef]
- Seo, J.; Gohn, A.M.; Dubin, O.; Takahashi, H.; Hasegawa, H.; Sato, R.; Rhoades, A.M.; Schaake, R.P.; Colby, R.H. Isothermal crystallization of poly(ether ether ketone) with different molecular weights over a wide temperature range. Polym. Cryst. 2019, 2, e10055. [Google Scholar] [CrossRef]
- Blundell, D.J.; Osborn, B.N. The morphology of poly(aryl-ether-ether-ketone). Polymer 1983, 24, 953–958. [Google Scholar] [CrossRef]
- Gordon, M.; Hillier, I.H. Mechanism of secondary crystallization of polymethylene. Philos. Mag. 1965, 11, 31–41. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of Phase Change. I General Theory. J. Chem. Phys. 1939, 7, 1103–1112. [Google Scholar] [CrossRef]
- Hoffman, J.D.; Lauritzen, J.I. Crystallization of bulk polymers with chain folding: Theory of growth of lamellar spherulites. J. Res. Natl. Bur. Stand. A 1961, 65A, 297–336. [Google Scholar] [CrossRef] [PubMed]
- Patel, R.M.; Spruiell, J.E. Crystallization kinetics during polymer processing—Analysis of available approaches for process modeling. Polym. Eng. Sci. 1991, 31, 730–738. [Google Scholar] [CrossRef]
- Yi, N.; Davies, R.; Chaplin, A.; McCutchion, P.; Ghita, O. Slow and fast crystallising poly aryl ether ketones (PAEKs) in 3D printing: Crystallisation kinetics, morphology, and mechanical properties. Addit. Manuf. 2021, 39, 101843. [Google Scholar] [CrossRef]
- Mohammadi, H.; Vincent, M.; Marand, H. Investigating the equilibrium melting temperature of linear polyethylene using the non-linear Hoffman-Weeks approach. Polymer 2018, 146, 344–360. [Google Scholar] [CrossRef]











Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benarbia, A.; Sobotka, V.; Boyard, N.; Roua, C. Modelling the Melting Kinetics of Polyetheretherketone Depending on Thermal History: Application to Additive Manufacturing. Polymers 2024, 16, 1319. https://doi.org/10.3390/polym16101319
Benarbia A, Sobotka V, Boyard N, Roua C. Modelling the Melting Kinetics of Polyetheretherketone Depending on Thermal History: Application to Additive Manufacturing. Polymers. 2024; 16(10):1319. https://doi.org/10.3390/polym16101319
Chicago/Turabian StyleBenarbia, Adel, Vincent Sobotka, Nicolas Boyard, and Christophe Roua. 2024. "Modelling the Melting Kinetics of Polyetheretherketone Depending on Thermal History: Application to Additive Manufacturing" Polymers 16, no. 10: 1319. https://doi.org/10.3390/polym16101319





