Multitemporal Field-Based Maize Plant Height Information Extraction and Verification Using Solid-State LiDAR
Abstract
:1. Introduction
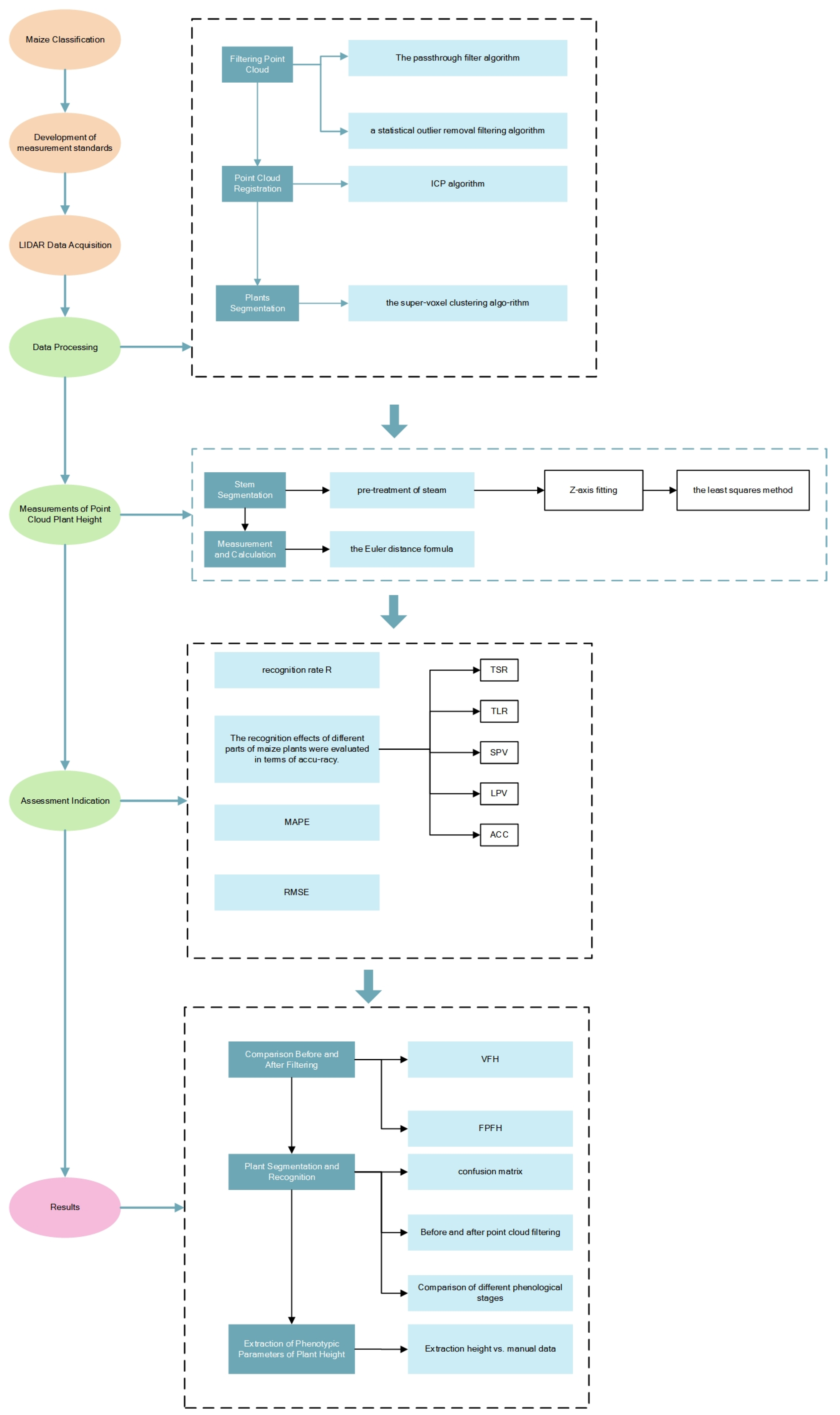
2. Materials and Methods
2.1. Data Acquisition
2.1.1. Point Cloud Data Acquisition
2.1.2. Standardization of Maize Plant Height Measurement
2.1.3. The Method of Extracting Multi-Phenotypic Maize Plant Height Information Using Solid-State LiDAR
2.2. Data Processing
2.2.1. Filtering Point Cloud
2.2.2. Point Cloud Registration
2.2.3. Plant Segmentation
2.3. Measurements of Point Cloud Plant Height
2.3.1. Stem Segmentation
2.3.2. Measurement and Calculation
2.4. Assessment Indication
3. Results
3.1. Comparison before and after Filtering
3.2. Plant Segmentation and Recognition
3.3. Extraction of Phenotypic Parameters of Plant Height
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, X.; Xu, K.; Liu, Y.; Guo, R.; Chen, L. Assessing the vulnerability and risk of maize to drought in China based on the AquaCrop model. Agric. Syst. 2021, 189, 103040. [Google Scholar] [CrossRef]
- Lan, Y.; Thomson, S.J.; Huang, Y.; Hoffmann, W.C.; Zhang, H. Current status and future directions of precision aerial application for site-specific crop management in the USA. Comput. Electron. Agric. 2010, 74, 34–38. [Google Scholar] [CrossRef]
- Lan, Y.; Thomson, S.J.; Huang, Y.; Hoffmann, W.C.; Zhang, H. Producing more grain with lower environmental costs. Nature 2014, 514, 486–489. [Google Scholar]
- Yang, W.; Duan, L.; Chen, G.; Xiong, L.; Liu, Q. Plant phenomics and high-throughput phenotyping: Accelerating rice functional genomics using multidisciplinary technologies. Curr. Opin. Plant Biol. 2013, 16, 180–187. [Google Scholar] [CrossRef] [PubMed]
- Großkinsky, D.K.; Svensgaard, J.; Christensen, S.; Roitsch, T. Plant phenomics and the need for physiological phenotyping across scales to narrow the genotype-to-phenotype knowledge gap. J. Exp. Bot. 2015, 66, 5429–5440. [Google Scholar] [CrossRef]
- Hall, R.D.; D’Auria, J.C.; Ferreira, A.C.S.; Gibon, Y.; Kruszka, D.; Mishra, P.; Van de Zedde, R. High-throughput plant phenotyping: A role for metabolomics. Trends Plant Sci. 2022, 27, 549–563. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Zhao, C.; Yang, G.; Yu, H.; Zhao, X.; Xu, B.; Niu, Q. Review of field-based phenotyping by unmanned aerial vehicle remote sensing platform. Trans. Chin. Soc. Agric. Eng. 2016, 32, 98–106. [Google Scholar]
- Li, W.; Niu, Z.; Huang, N.; Wang, C.; Gao, S.; Wu, C. Airborne LiDAR technique for estimating biomass components of maize: A case study in Zhangye City, Northwest China. Ecol. Indic. 2015, 57, 486–496. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, C.; Lu, X.; Wang, L.; Hao, Z.; Li, M.; Zhang, D.; Yong, H.; Zhu, H.; Weng, J.; et al. Dissecting the genetic basis underlying combining ability of plant height related traits in maize. Front. Plant Sci. 2018, 9, 1117. [Google Scholar] [CrossRef]
- Qiu, Q.; Sun, N.; Bai, H.; Wang, N.; Fan, Z.; Wang, Y.; Meng, Z.; Li, B.; Cong, Y. Field-based high-throughput phenotyping for maize plant using 3D LiDAR point cloud generated with a “Phenomobile”. Front. Plant Sci. 2019, 10, 554. [Google Scholar] [CrossRef]
- Deery, D.; Jimenez-Berni, J.; Jones, H.; Sirault, X.; Furbank, R. Proximal remote sensing buggies and potential applications for field-based phenotyping. Agronomy 2014, 4, 349–379. [Google Scholar] [CrossRef]
- Rebetzke, G.J.; Jimenez-Berni, J.A.; Bovill, W.D.; Deery, D.M.; James, R.A. High-throughput phenotyping technologies allow accurate selection of stay-green. J. Exp. Bot. 2016, 67, 4919–4924. [Google Scholar] [CrossRef] [PubMed]
- Sharma, L.K.; Bu, H.; Franzen, D.W.; Denton, A. Use of corn height measured with an acoustic sensor improves yield estimation with ground based active optical sensors. Comput. Electron. Agric. 2016, 124, 254–262. [Google Scholar] [CrossRef]
- Shafiekhani, A.; Kadam, S.; Fritschi, F.B.; DeSouza, G.N. Vinobot and vinoculer: Two robotic platforms for high-throughput field phenotyping. Sensors 2017, 17, 214. [Google Scholar] [CrossRef] [PubMed]
- Frasson, R.P.D.M.; Krajewski, W.F. 3D Digital Model of Maize Canopy. In Proceedings of the 7th World Congress on Computers in Agriculture Conference Proceedings, Reno, Nevada, 22–24 June 2009; pp. 22–29. [Google Scholar]
- Chambelland, J.C.; Dassot, M.; Adam, B.; Donès, N.; Balandier, P.; Marquier, A.; Saudreau, M.; Sonohat, G.; Sinoquet, H. A double-digitising method for building 3D virtual trees with non-planar leaves: Application to the morphology and light-capture properties of young beech trees (Fagus sylvatica). Funct. Plant Biol. 2008, 35, 1059–1069. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Zhao, Y.; Liu, S.; Li, Y.; Chen, S.; Lan, Y. Precision detection of dense plums in orchards using the improved YOLOv4 model. Front. Plant Sci. 2022, 13, 839269. [Google Scholar] [CrossRef] [PubMed]
- Omasa, K.; Hosoi, F.; Konishi, A. 3D LiDAR imaging for detecting and understanding plant responses and canopy structure. J. Exp. Bot. 2007, 58, 881–898. [Google Scholar] [CrossRef] [PubMed]
- Hosoi, F.; Nakabayashi, K.; Omasa, K. 3-D modeling of tomato canopies using a high-resolution portable scanning LiDAR for extracting structural information. Sensors 2011, 11, 2166–2174. [Google Scholar] [CrossRef] [PubMed]
- Niu, Q.; Feng, H.; Yang, G.; Li, C.; Yang, H.; Xu, B.; Zhao, Y. Monitoring plant height and leaf area index of maize breeding material based on UAV digital images. Trans. Chin. Soc. Agric. Eng. 2018, 34, 73–82. [Google Scholar]
- Hu, P.; Chapman, S.C.; Wang, X.; Potgieter, A.; Duan, T.; Jordan, D.; Guo, Y.; Zheng, B. Estimation of plant height using a high throughput phenotyping platform based on unmanned aerial vehicle and self-calibration: Example for sorghum breeding. Eur. J. Agron. 2018, 95, 24–32. [Google Scholar] [CrossRef]
- Miao, T.; Zhu, C.; Xu, T.; Yang, T.; Li, N.; Zhou, Y.; Deng, H. Stem-leaf segmentation and phenotypic trait extraction of maize shoots from 3D point cloud. arXiv 2020, arXiv:2009.03108. [Google Scholar]
- Qiu, R.; Zhang, M.; Wei, S.; Li, S.; Li, M.; Liu, G. Method for measurement of maize stem diameters based on RGB-D camera. Trans. Chin. Soc. Agric. Eng. 2017, 33, 170–176. [Google Scholar]
- Barabaschi, D.; Tondelli, A.; Desiderio, F.; Volante, A.; Vaccino, P.; Valè, G.; Cattivelli, L. Next generation breeding. Plant Sci. 2016, 242, 3–13. [Google Scholar] [CrossRef] [PubMed]
- Paulus, S.; Dupuis, J.; Mahlein, A.K.; Kuhlmann, H. Surface feature based classification of plant organs from 3D laserscanned point clouds for plant phenotypin. BMC Bioinform. 2013, 14, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Liu, J.; Zhang, B.; Wang, Y.; Yao, J.; Zhang, X.; Fan, B.; Li, X.; Hai, Y.; Fan, X. 3D reconstruction and phenotype measurement of maize seedlings based on multi-view image sequences. Front. Plant Sci. 2022, 13, 974339. [Google Scholar] [CrossRef] [PubMed]
- Gärtner, H.; Wagner, B.; Heinrich, I.; Denier, C. 3D-laser scanning: A new method t25o analyze coarse tree root systems. For. Snow Landsc. Res. 2009, 82, 95–106. [Google Scholar]
- Jin, S.; Su, Y.; Wu, F.; Pang, S.; Gao, S.; Hu, T.; Liu, J.; Guo, Q. Stem–leaf segmentation and phenotypic trait extraction of individual maize using terrestrial LiDAR data. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1336–1346. [Google Scholar] [CrossRef]
- Liu, J.; Pattey, E.; Jégo, G. Assessment of vegetation indices for regional crop green LAI estimation from Landsat images over multiple growing seasons. Remote Sens. Environ. 2012, 123, 347–358. [Google Scholar] [CrossRef]
- Brazeal, R.G.; Wilkinson, B.E.; Hochmair, H.H. A rigorous observation model for the risley prism-based livox Mid-40 LiDAR sensor. Sensors 2021, 21, 4722. [Google Scholar] [CrossRef]
- Cui, M.; Jia, B.; Liu, H.; Kan, X.; Zhang, Y.; Zhou, R.; Li, Z.; Yang, L.; Deng, D.; Yin, Z. Genetic mapping of the leaf number above the primary ear and its relationship with plant height and flowering time in maize. Front. Plant Sci. 2017, 8, 1437. [Google Scholar] [CrossRef]
- Yu, Z.; Cao, Z.; Wu, X.; Bai, X.; Qin, Y.; Zhuo, W.; Xiao, Y.; Zhang, X.; Xue, H. Automatic image-based detection technology for two critical growth stages of maize: Emergence and three-leaf stage. Agric. For. Meteorol. 2013, 174, 65–84. [Google Scholar] [CrossRef]
- Zhang, K.X.; Chen, H.; Wu, H.; Zhao, X.Y.; Zhou, C.A. Point cloud registration method for maize plants based on conical surface fitting—ICP. Sci. Rep. 2022, 12, 6852. [Google Scholar] [CrossRef] [PubMed]
- Miknis, M.; Davies, R.; Plassmann, P.; Ware, A. Near real-time point cloud processing using the PCL. In Proceedings of the 2015 International Conference on Systems, Signals and Image Processing (IWSSIP), London, UK, 10–12 September 2015; pp. 153–156. [Google Scholar]
- Rusu, R.B.; Cousins, S. 3D is here: Point Cloud Library (PCL). In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011. [Google Scholar]
- Carrilho, A.C.; Galo, M.; Santos, R.C. Statistical outlier detection method for airborne LiDAR data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 87–92. [Google Scholar] [CrossRef]
- Balta, H.; Velagic, J.; Bosschaerts, W.; De Cubber, G.; Siciliano, B. Fast statistical outlier removal based method for large 3D point clouds of outdoor environments. IFAC-Pap. 2018, 51, 348–353. [Google Scholar] [CrossRef]
- Särkkä, S.; Svensson, L. Bayesian Filtering and Smoothing; Cambridge University Press: Cambridge, UK, 2023; Volume 17. [Google Scholar]
- Liu, X.; Ma, Q.; Wu, X.; Hu, T.; Liu, Z.; Liu, L.; Guo, Q.; Su, Y. A novel entropy-based method to quantify forest canopy structural complexity from multiplatform LiDAR point clouds. Remote Sens. Environ. 2022, 282, 113280. [Google Scholar] [CrossRef]
- Nurunnabi, A.; Sadahiro, Y.; Lindenbergh, R.; Belton, D. Robust cylinder fitting in laser scanning point cloud data. Measurement 2019, 138, 632–651. [Google Scholar] [CrossRef]
- Jin, Y.H.; Lee, W.H. Fast cylinder shape matching using random sample consensus in large scale point cloud. Appl. Sci. 2019, 9, 974. [Google Scholar] [CrossRef]
- Rampriya, R.S.; Suganya, R. Segmentation of 3D point cloud data based on SuperVoxel technique. Procedia Comput. Sci. 2020, 171, 427–435. [Google Scholar] [CrossRef]
- Papon, J.; Abramov, A.; Schoeler, M.; Worgotter, F. Voxel cloud connectivity segmentation-SuperVoxel for point clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23-28 June 2013; pp. 2027–2034. [Google Scholar]
- Wen, L.; He, L.; Gao, Z. Research on 3D point cloud de-distortion algorithm and its application on Euclidean clustering. IEEE Access 2019, 7, 86041–86053. [Google Scholar] [CrossRef]
- Han, H.; Han, X.; Sun, F.; Huang, C. Point cloud simplification with preserved edge based on normal vector. Opt. -Int. J. Light Electron Opt. 2015, 126, 2157–2162. [Google Scholar] [CrossRef]
- Liakos, K.G.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine learning in agriculture: A review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; Lin, S.; Wu, H.; Cao, G. Point Cloud Registration Based on Fast Point Feature Histogram Descriptors for 3D Reconstruction of Trees. Remote Sens. 2023, 15, 3775. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Chen, H.; Li, D.; Wu, M.; Zhao, W. Remote estimation of canopy height and aboveground biomass of maize using high-resolution stereo images from a low-cost unmanned aerial vehicle system. Ecol. Indic. 2016, 67, 637–648. [Google Scholar] [CrossRef]
- Tilly, N.; Aasen, H.; Bareth, G. Fusion of plant height and vegetation indices for the estimation of barley biomass. Remote Sens. 2015, 7, 11449–11480. [Google Scholar] [CrossRef]
- Hu, X.; Gu, X.; Sun, Q.; Yang, Y.; Qu, X.; Yang, X.; Guo, R. Comparison of the performance of Multi-source 3D structural data in the application of monitoring maize lodging. Comput. Electron. Agric. 2023, 208, 107782. [Google Scholar] [CrossRef]
- Madec, S.; Baret, F.; de Solan, B.; Thomas, S.; Dutartre, D.; Jezequel, S.; Comar, A. High-throughput phenotyping of plant height: Comparing unmanned aerial vehicles and ground LiDAR estimates. J. Exp. Bot. 2017, 68, 5733–5747. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.; Yang, W.; Wu, J.; Chen, P.; Lan, Y.; Zhang, L. Canopy laser interception compensation mechanism—UAV LiDAR precise monitoring method for cotton height. Agronomy 2023, 13, 2584. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, W.; Yang, G.; Lei, L.; Han, S.; Xu, W.; Chen, R.; Zhang, C.; Yang, H. Maize ear height and ear–plant height ratio estimation with LiDAR data and vertical leaf area profile. Remote Sens. 2023, 15, 964. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, X.; Shi, W.; Song, S.; Cardenas-Tristan, A.; Li, K. An accurate and robust region-growing algorithm for plane segmentation of TLS point clouds using a multiscale tensor voting method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4160–4168. [Google Scholar] [CrossRef]
- Lei, L.; Li, Z.; Yang, G.; Yang, H. High-Throughput extraction of the distributions of leaf base and inclination angles of maize in the field. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–28. [Google Scholar] [CrossRef]









| Parameters | Values |
|---|---|
| Laser Wavelength | 905 nm |
| FOV | 38.4° Circular |
| Range Precision (1σ@20 m) | 2 cm |
| Angular Accuracy | <0.1° |
| Point Rate | 100,000 points/s |
| Weight | Approx. 710 g |
| Size | 88 × 69 × 76 mm |
| Stem Recall Rate | Leaf Recall Rate | Precision of Stem | Precision of Leaf | Accuracy | Segmentation Successful Rate | |
|---|---|---|---|---|---|---|
| Before | 88.89% | 84.21% | 84.21% | 88.89% | 86.55% | 64.00% |
| After | 100% | 91.30% | 91.30% | 100% | 95.65% | 84.00% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Chen, S.; Zhou, B.; He, H.; Zhao, Y.; Wang, Y.; Zhou, X. Multitemporal Field-Based Maize Plant Height Information Extraction and Verification Using Solid-State LiDAR. Agronomy 2024, 14, 1069. https://doi.org/10.3390/agronomy14051069
Zhao J, Chen S, Zhou B, He H, Zhao Y, Wang Y, Zhou X. Multitemporal Field-Based Maize Plant Height Information Extraction and Verification Using Solid-State LiDAR. Agronomy. 2024; 14(5):1069. https://doi.org/10.3390/agronomy14051069
Chicago/Turabian StyleZhao, Junhong, Shengde Chen, Bo Zhou, Haoxiang He, Yingjie Zhao, Yu Wang, and Xingxing Zhou. 2024. "Multitemporal Field-Based Maize Plant Height Information Extraction and Verification Using Solid-State LiDAR" Agronomy 14, no. 5: 1069. https://doi.org/10.3390/agronomy14051069





