Health Risk Prediction of Operational Subsea Tunnel Structure Based on Bayesian Network
Abstract
1. Introduction
2. Risk Prediction Method
2.1. Discrete Bayesian Network Model
2.2. Conditional Probability
3. Health Risk Prediction Process of Operational Subsea Tunnel Structure
3.1. Health Risk Prediction Steps
- (1)
- Identifying the risk factors that affect the health of subsea metro shield tunnel structure in operation, and determining the state space of each risk factor. Establishing a risk indicator system for the health risks of the operational shield tunnel structure based on the relationships of these risk factors.
- (2)
- Using the probability of risk occurrence to establish the likelihood rating standards for the operational health risks of the subsea metro shield tunnel structure.
- (3)
- Learning the Bayesian network structure for the operational health risks of subsea metro shield tunnel structure.
- (4)
- Learning the parameters of the Bayesian network for the health risks of operational subsea metro shield tunnel structure by computing the conditional probabilities of the child nodes.
- (5)
- Inferring the probability of health risks for the operational subsea metro shield tunnel structure.
3.2. Risk Factors Identification
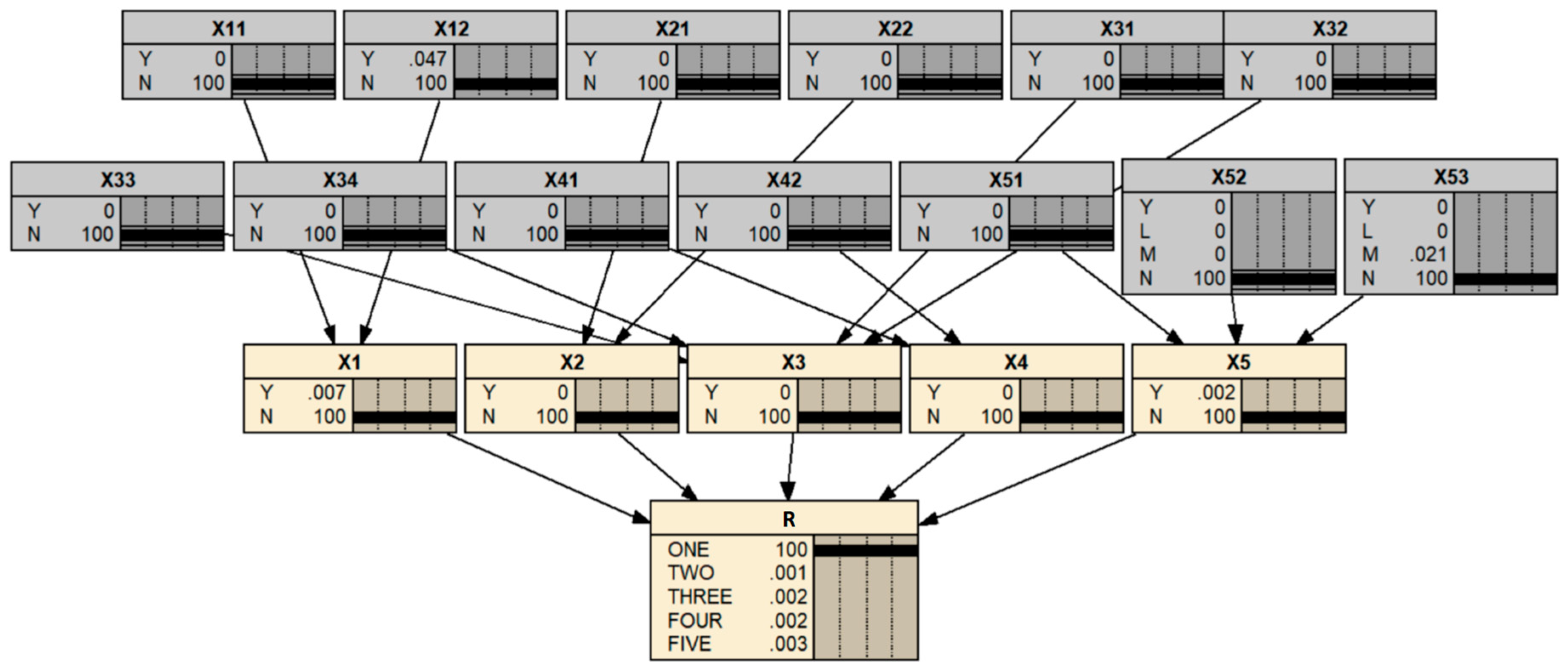
3.3. Risk Prediction Based on Bayesian Networks
4. Validation of Health Risk Prediction Model for Operational Subsea Tunnel Structures
5. Case Study
5.1. Overview of the Structural Engineering of the Dalian Subsea Metro Tunnel
5.2. General Situation of the Health Monitoring System of the Dalian Subsea Tunnel Structure
5.3. Health Risk Prediction of the Dalian Subsea Tunnel Structure
6. Conclusions and Suggestion
- (1)
- The health risk prediction method for the operational subsea metro shield tunnel structure is proposed based on a discrete Bayesian network, Noisy-OR gate model, and Noisy-MAX model, combining with engineering detection and monitoring data of 13 risk factors in five aspects such as structure mechanical condition, material properties, structural integrity state, environmental state, and structural deformation state.
- (2)
- The Noisy-OR gate and Noisy-MAX models are used to calculate the conditional probabilities of variables, which ensures that the workload of experts increases linearly with the number of parent nodes, rather than exponentially. And the workload of experts is significantly reduced.
- (3)
- Based on the proposed health risk prediction method and expert experience with tunnel structures of poor health status, it is calculated that the probability of structural health risk is at level 4 and level 5, reaching 22.9% and 32.5%, respectively. It shows the rationality of the prediction model proposed in this paper.
- (4)
- The proposed health risk prediction method is used to predict the health risk of the Dalian subsea metro tunnel structure. The health risk prediction outcomes are consistent with the actual operational status, which verifies the rationality of the method and provides decision support for health risk management.
- (5)
- Based on the proposed health risk prediction method, health risk prediction is carried out by combination with engineering field detection and monitoring data, which effectively reflect the real service state of the shield tunnel structure.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xiao, M.Q. Reprcsentativc projecis and development trend of underwater shield lunnels in China. Tunn. Constr. 2018, 38, 360–371. [Google Scholar]
- Chen, J.Q.; Feng, X.Y.; Wei, H.; Feng, H.H. Statistics on underwater tunnels in China. Tunn. Constr. 2021, 41, 483–516. [Google Scholar]
- Li, J.; Wei, D.H.; Cao, Y.Y.; Du, H.G. Geophysical prospecting for Xiang an Submarine Tunnel in Xiamen. J. Railw. Eng. Soc. 2010, 144, 27–31. [Google Scholar]
- Pan, G.D.; Zhou, S.M.; Duan, W.Z. Risk assessment and contrl of grouting construction of Qingdao Jiaozhouwan tunnel in subsea zone. J. Shi Jia Zhang Tiedao Univ. (Nat. Sci.) 2010, 23, 53–57. [Google Scholar]
- Xu, H.Y. Research on Risk Assessment of Operational Tunnelucture Based on Bayesian Network. Master’s Thesis, Hu Bei University of Technology, Wuhan, China, 2023. [Google Scholar]
- Hou, J.Y.; Yang, Q.X.; Guo, C. Study on Comprehensive Evaluation of Operation Safety of Long Highway Tunnel. Railw. Stand. Des. 2015, 59, 88–91+109. [Google Scholar]
- Luo, Y.; Li, Y.W.; Yuan, J.W.; Liu, D.G.; Wang, M.N. Study on Risk Assessment of Highway Tunnel Operational Safety. Mod. Tunn. Technol. 2016, 53, 25–30. [Google Scholar]
- Pan, Z.Z.; Wu, H.B.; Liao, J.H.; Wang, R.G. Study of Risk Management Techniques for Expressway Tunnels at Operation Phase. High Way 2017, 62, 141–146. [Google Scholar]
- Wang, Z.J.; Wang, R.L.; Shu, Y.X.; Wei, R.; Wang, Z.J.; Tan, J. Study on operation safety risk assessment of the extra-long expressway tunnel and tunnel group. Mod. Tunn. Technol. 2019, 56 (Suppl. S2), 36–43. [Google Scholar]
- Xu, C.; Liu, X.L.; Wang, E.Z.; Wang, S.J. Prediction and classification of strain mode rockburst based on five-factor criterion and combined weight-ideal point method. Chin. J. Geotech. Eng. 2017, 39, 2245–2252. [Google Scholar]
- Luo, Y.P.; Gao, G.F.; Wu, H.L. Study on Fuzzy evaluating system of traffic safety in higyway tunnel. J. Shi Jia Zhang Tiedao Univ. 2006, 19, 75–79. [Google Scholar]
- Gong, H.J. Reseath of Operation Safety Comprehensive Evaluation on the Tunnel of Freeway. Ph.D. Thesis, Chang’an University, Xi’an, China, 2009. [Google Scholar]
- Cheng, Y.; Liu, Z.B.; Liu, S.Y.; Cai, G.J.; Tong, L.Y. Risk recognition of construction of large-span and shallow buried-highway tunnels based on analytic hierarchy process. Chin. J. Geotech. Eng. 2011, 33 (Suppl. S1), 198–202. [Google Scholar]
- Khademi Hamidi, J.; Shahriar, K.; Rezai, B.; Rostami, J.; Bejari, H. Risk assessment based selection of rock TBM for adverse geological conditions using Fuzzy-AHP. Bull. Eng. Geol. Environ. 2010, 69, 523–532. [Google Scholar] [CrossRef]
- Aliahmadi, A.; Sadjadi, S.J.; Jafari-Eskandari, M. Design a new intelligence expert decision making using game theory and fuzzy AHP to risk management in design, construction, and operation of tunnel projects (case studies: Resalat Tunnel). Int. J. Adv. Manuf. Technol. 2011, 53, 789–798. [Google Scholar] [CrossRef]
- Liu, H.; Sun, S.M.; Zhang, X.M. Study and application of safety fuzzy assessment model for highway tunnel construction. Mod. Tunneling Technol. 2008, 45, 5–9. [Google Scholar]
- Liu, W. Risk Assessment and Its Application in Mountain Highway Tunnel Construction. Master’s Thesis, Changan University, Xi’an, China, 2011. [Google Scholar]
- Ma, A.Z. Research on Safety Risk Assessment and Its Application in Long and Large Tunnel Construction. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2016. [Google Scholar]
- Tian, Y.; Ma, R.J.; Chen, A.R. Safety risk assessment for interactive influences between adjacent and parallel high-speed railway bridges and highway. J. Vib. Shock. 2016, 35, 69–75. [Google Scholar]
- Hyun, K.C.; Min, S.; Choi, H. Risk analysis using fault-tree analysis (FTA) and analytic hierarchy process (AHP) applicable to shield TBM tunnels. Tunn. Undergr. Space Technol. 2015, 49, 121–129. [Google Scholar] [CrossRef]
- Wang, Z.C.; Lu, B.Q.; Li, S.C. Risk assessment for an underground crude oil storage facility with water-curtaining system during construction phase. Chin. J. Geotech. Eng. 2015, 37, 1057–1067. [Google Scholar]
- Špačková, O.; Novotná, E.; Šejnoha, M. Probabilistic models for tunnel construction risk assessment. Adv. Eng. Softw. 2013, 62, 72–84. [Google Scholar] [CrossRef]
- Jiang, S.H.; Yang, J.H.; Yao, C. Quantitative risk assessment of slop failure considering spatial variability of soil properties. Eng. Mech. 2018, 35, 136–147. [Google Scholar]
- Kampmann, J.; Eskesen, S.; Summers, J. Risk assessment helps select the contractor for the Copenhagen Metro System. Proc. World Tunn. Congr. 1998, 98, 123–128. [Google Scholar]
- Xiang, W.; Zhou, W. Bayesian network model for predicting probability of third-party damage to underground pipelines and learning model parameters from incomplete datasets. Reliab. Eng. Syst. Saf. 2021, 20, 107–262. [Google Scholar] [CrossRef]
- Lu, X.Y.; Xu, C.S.; Hou, B.W. Risk assessment of metro construction based on dynamic Bayesian network. Chin. J. Geotech. Eng. 2022, 44, 492–501. [Google Scholar]
- Xu, X.L.; Ma, W.B.; Cai, D.G. Research on the whole life cycle detection and monitoring system of railway tunnel. Mod. Tunn. Technol. 2021, 58, 31–40. [Google Scholar]
- Huang, Z.; Fu, H.L.; Huang, H.C.W. A method for evaluating the structural health status of shield tunnel in operating subway. J. Undergr. Space Eng. 2018, 14, 1410–1418. [Google Scholar]
- Zagorecki, A.; Druzdzel, M.J. An empirical study of probability elicitation under Noisy-or assumption. In Proceedings of the American Association for Artificial Intelligence Flairs Conference, Miami Beach, FL, USA, 17–19 May 2004. [Google Scholar]
- Rui, M.; Yadi, W. Knowledge engineering for Bayesian networks: How common are Noisy-max distributions in practice. IEEE Trans. Syst. Man Cybern. Syst. 2013, 43, 186–195. [Google Scholar]
- Gao, X.L.; Chen, H.Y. Discrete Dynamic Bayesian Network Inference and Its Application; National Defense Industry Press: Beijing, China, 2016. [Google Scholar]
- Weber, P.; Medina-Oliva, G.; Simon, C.; Lung, B. Overview on Bayesian networks applications for dependability, risk analysis and maintenance areas. Eng. Appl. Artif. Intell. 2012, 25, 671–682. [Google Scholar] [CrossRef]
- GB 50652-2011; Code for Risk Management of Underground Works in Urban Rail Transit. China Standards Press: Beijing, China, 2011.
- Zhang, L.W.; Guo, H.H. Introduction to Bayesian Networks; Science Press: Beijing, China, 2006. [Google Scholar]
- GB 39559.3-2020; Specifications for Operational Monitoring of Urban Rail Transit Facilities—Part 3: Tunnel. China Standards Press: Beijing, China, 2020.







| Level | Tunnel Structure Status | Disposal Measures |
|---|---|---|
| Level 1 | Excellent | Normal operation, regular monitoring |
| Level 2 | Good | Normal operation, enhanced monitoring |
| Level 3 | Fair | Normal operation, requiring maintenance |
| Level 4 | Poor | Conducting a safety assessment to determine whether to restrict the use |
| Level 5 | Very poor | Conducting a safety assessment to determine whether to stop the use |
| State | Tunnel Headroom Convergence | Tunnel Vertical Displacement |
|---|---|---|
| N | <6‰ | <1 mm/a |
| M | ≥6‰, <9‰ | ≥1 mm/a, <3 mm/a |
| L | ≥9‰, <12‰ | ≥3 mm/a, <10 mm/a |
| Y | ≥12‰ | ≥10 mm/a |
| X11 | X12 | X1 = Y | X1 = N |
|---|---|---|---|
| Y | Y | 0.564 | 0.436 |
| Y | N | 0.205 | 0.795 |
| N | Y | 0.452 | 0.548 |
| N | N | 0.000 | 1.000 |
| Stress State X1 | Material Performance X2 | Integrity State X3 | Environmental Conditions X4 | Deformation State X5 | Likelihood Level of Health Risk | ||||
|---|---|---|---|---|---|---|---|---|---|
| Impossible (r = 1) | Rare (r = 2) | Occasional (r = 3) | Possible (r = 4) | Frequent (r = 5) | |||||
| Y | Y | Y | Y | Y | 0.000 | 0.000 | 0.004 | 0.071 | 0.925 |
| Y | Y | Y | Y | N | 0.000 | 0.000 | 0.006 | 0.072 | 0.922 |
| Y | Y | Y | N | Y | 0.000 | 0.002 | 0.023 | 0.220 | 0.754 |
| Y | Y | Y | N | N | 0.000 | 0.004 | 0.030 | 0.212 | 0.754 |
| Y | Y | N | Y | Y | 0.000 | 0.001 | 0.009 | 0.097 | 0.893 |
| Y | Y | N | Y | N | 0.000 | 0.001 | 0.012 | 0.098 | 0.889 |
| Y | Y | N | N | Y | 0.000 | 0.008 | 0.048 | 0.277 | 0.666 |
| Y | Y | N | N | N | 0.002 | 0.016 | 0.058 | 0.273 | 0.651 |
| Y | N | Y | Y | Y | 0.000 | 0.001 | 0.019 | 0.107 | 0.873 |
| Y | N | Y | Y | N | 0.000 | 0.003 | 0.024 | 0.106 | 0.867 |
| Y | N | Y | N | Y | 0.000 | 0.016 | 0.098 | 0.284 | 0.601 |
| Y | N | Y | N | N | 0.002 | 0.031 | 0.120 | 0.264 | 0.584 |
| Y | N | N | Y | Y | 0.000 | 0.005 | 0.039 | 0.136 | 0.819 |
| Y | N | N | Y | N | 0.002 | 0.009 | 0.048 | 0.130 | 0.812 |
| Y | N | N | N | Y | 0.009 | 0.058 | 0.188 | 0.311 | 0.435 |
| Y | N | N | N | N | 0.042 | 0.090 | 0.205 | 0.253 | 0.410 |
| Categories of risk factors | X1 | X2 | X3 | X4 | ||||||
| Risk factor indicators | X11 | X12 | X21 | X22 | X31 | X32 | X33 | X34 | X41 | X42 |
| Risk factor status | Y | Y | Y | Y | Y | Y | Y | Y | Y | Y |
| Prior probability | 28 | 32 | 33 | 25 | 22 | 21 | 35 | 35 | 32 | 33 |
| Categories of risk factors | X5 | |||||||||
| Risk factor indicators | X51 | X52 | X53 | |||||||
| Risk factor status | Y | N | M | L | Y | N | M | L | Y | |
| Prior probability | 42 | 13 | 20 | 32 | 35 | 10 | 21 | 34 | 35 | |
| Number | Monitoring Content | Monitoring Index | Sensor Type |
|---|---|---|---|
| 1 | Structural mechanical condition | Internal force in steel bars | Instrumented rebar |
| 2 | Strain of concrete | Concrete strain meter | |
| 3 | Structural load | Surrounding rock pressure | Total pressure cell |
| 4 | Surrounding rock pore water pressure | Vibrating wire piezometer | |
| 5 | Durability of structure | Steel corrosion | Anode ladder |
| 6 | Structural vibration | Acceleration | Accelerometer |
| 7 | Structure leaking | Leakage | Distributed optical fiber |
| 8 | Structural distortion | Segment misalignment, Tunnel vertical displacement | Distributed optical fiber |
| Categories of risk factors | X1 | X2 | X3 | X4 | ||||||
| Risk factor indicators | X11 | X12 | X21 | X22 | X31 | X32 | X33 | X34 | X41 | X42 |
| Risk factor status | Y | Y | Y | Y | Y | Y | Y | Y | Y | Y |
| Measured probability | 0 | 0.001 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Categories of risk factors | X5 | |||||||||
| Risk factor indicators | X51 | X52 | X53 | |||||||
| Risk factor status | Y | N | M | L | Y | N | M | L | Y | |
| Measured probability | 0 | 1 | 0 | 0 | 0 | 0.9999 | 0.0001 | 0 | 0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ni, H.; Li, X.; Huang, J.; Zhou, S. Health Risk Prediction of Operational Subsea Tunnel Structure Based on Bayesian Network. Buildings 2024, 14, 1475. https://doi.org/10.3390/buildings14051475
Ni H, Li X, Huang J, Zhou S. Health Risk Prediction of Operational Subsea Tunnel Structure Based on Bayesian Network. Buildings. 2024; 14(5):1475. https://doi.org/10.3390/buildings14051475
Chicago/Turabian StyleNi, Hongmei, Xia Li, Jingqi Huang, and Shuming Zhou. 2024. "Health Risk Prediction of Operational Subsea Tunnel Structure Based on Bayesian Network" Buildings 14, no. 5: 1475. https://doi.org/10.3390/buildings14051475
APA StyleNi, H., Li, X., Huang, J., & Zhou, S. (2024). Health Risk Prediction of Operational Subsea Tunnel Structure Based on Bayesian Network. Buildings, 14(5), 1475. https://doi.org/10.3390/buildings14051475






