Study and Experiment on Screen Surface Homogenization Technology of Dislodged Material Based on Longitudinal Flow Threshing
Abstract
:1. Introduction
2. Structure and Working Principle of Longitudinal Axial Flow Stripper Reflux Homogenizing Device
3. Determination of the Main Parameters of the Reflux Load Homogenizing Device
3.1. Determination of Reflux Plate Inclination Angle
3.2. Determination of Step Plate Spacing
3.3. Determination of Step Plate Height
3.4. Determination of Reflux Plate Length
3.5. Determination of Return Plate Motor Speed
4. EDEM-Based Simulation of Optimised Tests
4.1. Model and Material Properties
4.2. Reflux Plate Simulation Model
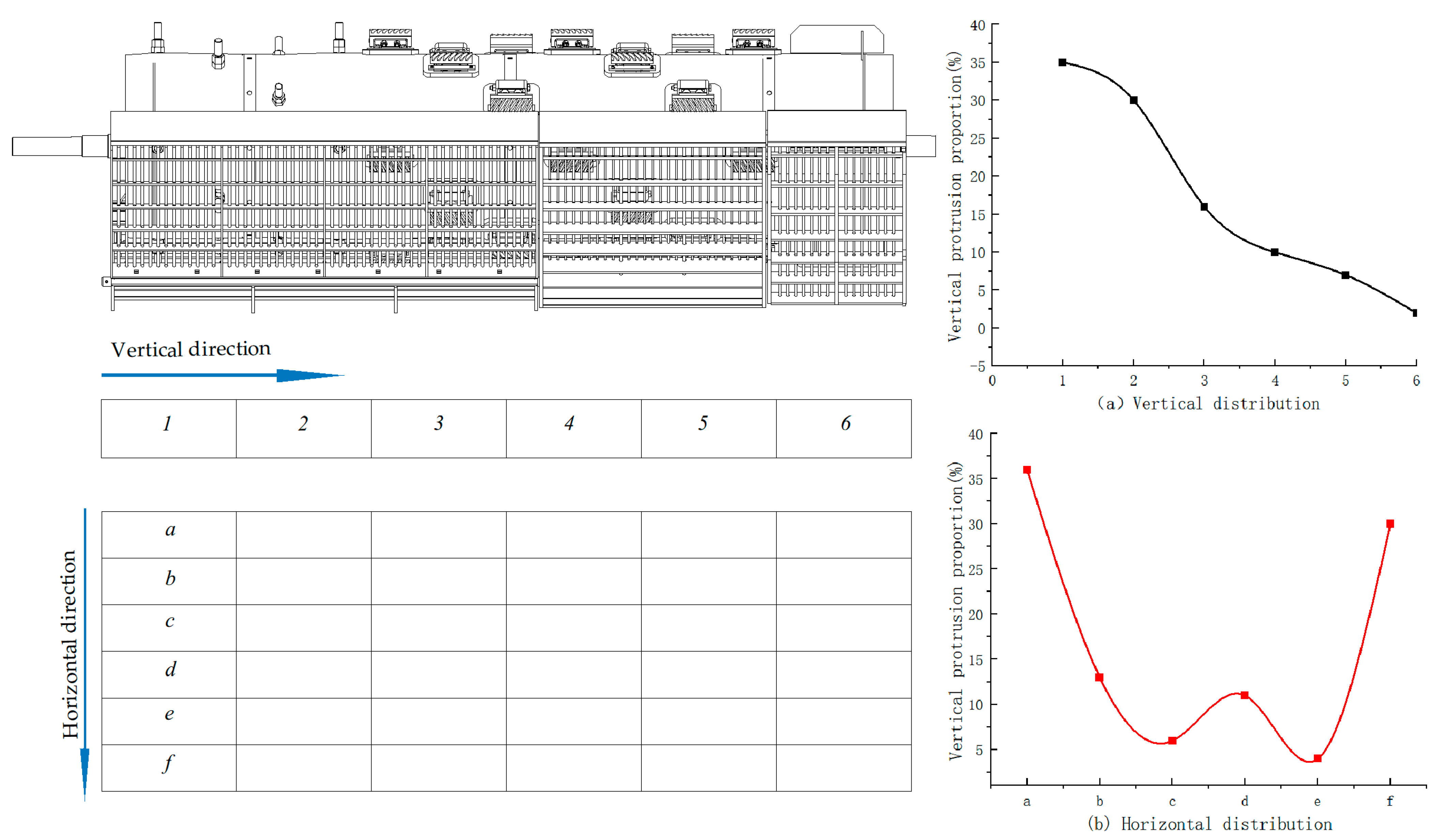
4.3. Effect of Stepped Plate Angle on the Distribution of Exudates
4.4. Optimisation of Stepped Plate Angle Parameters
5. Bench Test
5.1. Test Conditions
5.2. Test Factors and Indicators
5.3. Test Methods
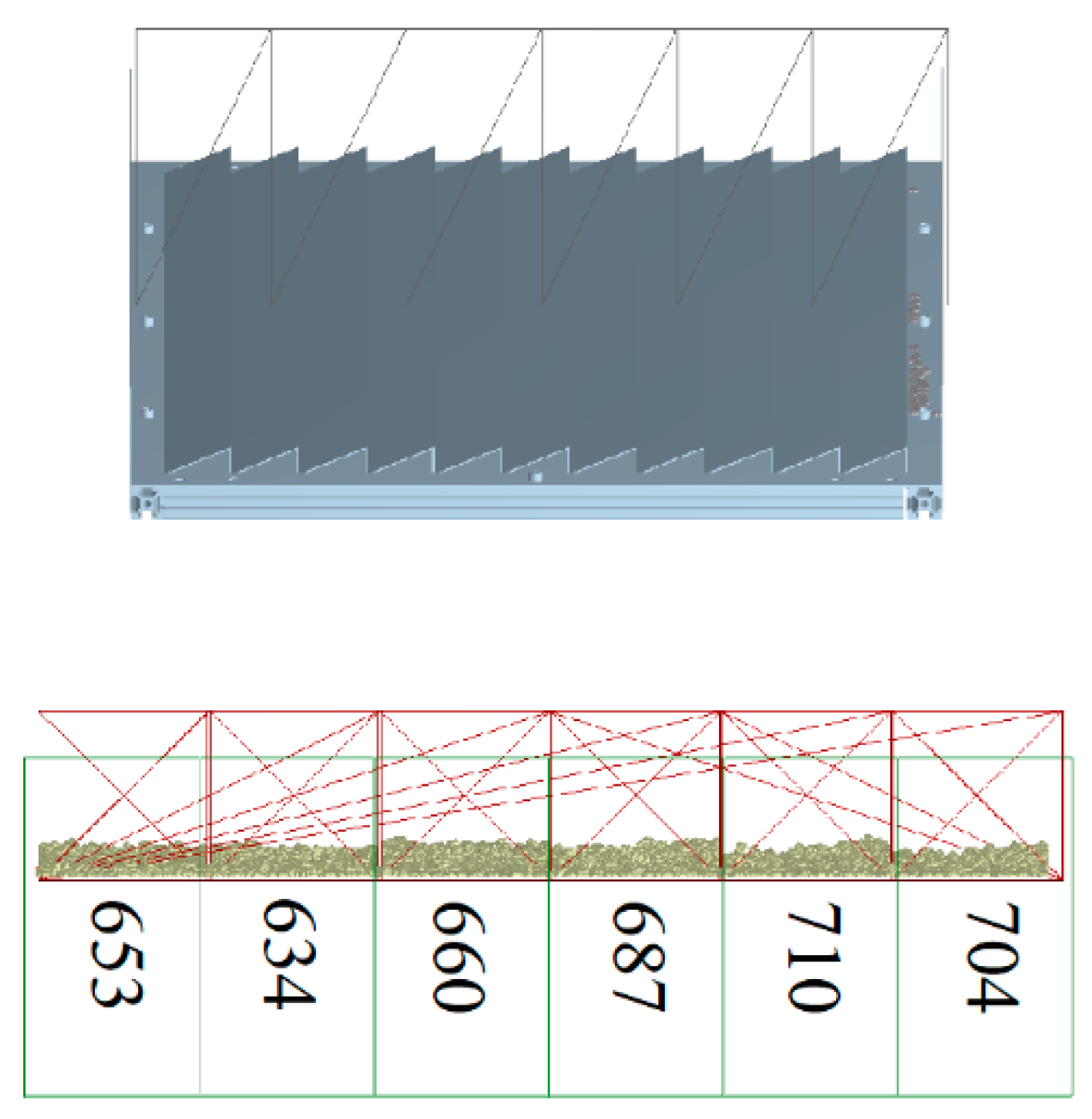
5.4. Analysis of Test Results
5.5. Optimization of Parameters
6. Field Trial Validation
7. Conclusions
- Aiming at the problems of uneven distribution of dislodged material on the screen surface of longitudinal flow grain combine harvester, a large difference in material clearing time, and large clearing loss, a dislodged material homogenizing device that can realize reflux and homogenization of dislodged material at the rear of longitudinal flow has been developed. The structure and motion parameters of the reflux plate were determined, and simulation tests were carried out to verify the optimal parameters of the angle of the stepped plate.
- The relevant test bench was set up, and the Box-Behnken test method was adopted to determine the influence law of each factor on the operating effect and the optimal parameter combination, and the results showed that the tilting angle of the reflux plate, the motor speed and the amplitude had a significant influence on the distribution uniformity of the material on the screen surface; the optimal parameter combination was determined to be the angle of the reflux plate configuration at 28.7°, the motor speed at 247 r/min, and the seed inclusion rate of 0.48% at an amplitude of 18.3 mm. The optimum combination of parameters was determined to be 28.7°, 247 r/min, 18.3 mm, and 0.48% of impurity rate.
- Under this condition, field tests were carried out to verify the results, which were basically consistent with the results of the previous tests, and the error between the optimized test results and the verification results was less than 5%, which proved that it could effectively improve the performance of scavenging and reduce the rate of impurity content.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Li, X.P.; Zhang, W.T.; Xu, S.D. Low-Damage Corn Threshing Technology and Corn Threshing Devices: A Review of Recent Developments. Agriculture 2023, 13, 1006. [Google Scholar] [CrossRef]
- Fu, J.W.; Xie, G.; Ji, C. Study on the Distribution Pattern of Threshed Mixture by Drum-Shape Bar-Tooth Longitudinal Axial Flow Threshing and Separating Device. Agriculture 2021, 11, 756. [Google Scholar] [CrossRef]
- Yue, D.; Wang, Q.H.; He, Q.H. A Study of the Distribution of the Threshed Mixture by a Double Longitudinal Axial Flow Corn Threshing Device. Agriculture 2024, 14, 166. [Google Scholar] [CrossRef]
- Hao, J.F.; Han, Z.D.; Liu, G.M. Research Status and Development Trend of Cleaning Device of Corn Thresher. J. Anhui Agric. 2016, 44, 322–324+330. [Google Scholar] [CrossRef]
- Hao, F.P.; Chen, Z. Actuality of Domestic and Foreign Corn Harvester. Agric. Mech. Res. 2007, 10, 206–208. [Google Scholar]
- Cui, T.; Fan, C.L.; Zhang, D.X. Research Progress of Maize Mechanized Harvesting Technology. J. Agric. Mach. 2019, 50, 1–13. [Google Scholar]
- Chen, Z.; Hao, F.P.; Wang, F.D. Development of Technology and Equipment of Corn Harvester in China. J. Agric. Mach. 2012, 43, 44–50. [Google Scholar]
- Wang, W.Z.; Liu, W.W.; Yuan, L.H. Calibration of discrete element parameters of wheat plantsat harvest period based on EDEM. J. Henan Agric. Univ. 2021, 55, 64–72. [Google Scholar] [CrossRef]
- Zhou, Y. Design and Test of Automatic Equidistribution Device for Tangential and Longitudinal Flow Grain-MOG Mixture. Bachelor’s Thesis, Jiangsu University, Jiangsu, China, 2019. [Google Scholar]
- Zhang, M.; Jin, C.; Liang, S.; Tang, Q.; Wu, C. Parameter optimization and experiment on air-screen cleaning device of rapeseed combine harvester. Trans. Chin. Soc. Agric. Eng. 2015, 31, 8–15. [Google Scholar]
- Li, M.M. Unusual Unseen Harvesting Shows Its Promise—Krasse LEXION 770 Combine Harvester Helps 2012 Autumn Harvest in 852 Farms. Agric. Mach. 2012, 86–89. [Google Scholar] [CrossRef]
- CaseIH. Case AF4000 Series Axial Drum Combine Harvester, Multi-Purpose. Agric. Mach. 2020, 20. [Google Scholar] [CrossRef]
- Claas. All-round Harvesting King—CLAAS LEXION 700 Series Combine Harvester. Agric. Mach. 2015, 51. [Google Scholar]
- Wang, Y.H. High-performance Kubota PRO488 combine harvester. Agric. Mach. 2002, 42. [Google Scholar]
- Li, B.H.; Yi, S.J.; Jiang, N. Axial flow threshing and separating device discharged material along the drum tangential distribution law. Mod. Agric. 2005, 10, 31–32. [Google Scholar]
- Guo, Y.; Li, Y.M.; Li, H.C. The Radial Distribution Regularities of Emerging Object with Longitudinal Axial Flow Threshing and Separating Device. Res. Agric. Mech. 2011, 33, 110–112. [Google Scholar] [CrossRef]
- Geng, D.Y.; He, K.; Wang, Q. Design and Experiment on Transverse Axial Flow Flexible Threshing Device for Corn. J. Agric. Mach. 2019, 50, 101–108. [Google Scholar]
- Fu, W.; Yang, L.D.; He, R. Analysis and Improvement of Oscillating Plate of Grain Combine Harvester Journal of Shihezi University. Natureal Sci. 2012, 30, 249–251. [Google Scholar] [CrossRef]
- Fan, C.L.; Cui, T.; Zhang, D.X. Design and Experiment of Double-layered Reverse Cleaning Device for Axial Flow Combine Harvester. J. Agric. Mach. 2018, 49, 239–248. [Google Scholar]
- Cheng, C.; Fu, J.; Chen, Z. Optimization Experiment on Cleaning Device Parameters of Corn Kernel Harvester. J. Agric. Mach. 2019, 50, 151–158. [Google Scholar]
- Ma, Z.; Li, Y.M.; Xu, L.Z. Discrete-element method simulation of agricultural particles’ motion in variable-amplitude screen box. Comput. Electron. Agric. 2015, 118, 92–99. [Google Scholar] [CrossRef]
- Wang, D.J.; Choe, J.S. Development Status and Trend of Large Feed Grain Axial Threshing Equipmen. Agric. Technol. Equip. 2017, 330, 81–84. [Google Scholar]
- Zhao, H.S.; Bao, Y.X.; Chen, S.Y.; Yang, X.X. Current situation and development tendency of high-frequency vibration screen technology and equipments at home and abroad. Min. Mach. 2011, 39, 83–88. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Lai, Y.J.; Zhang, K.; Sun, J.J. Research on The Axial Direction Distribution Regularities of Emerging Object with Axial Flow Threshing Installation. J. Heilongjiang Bayi Agric. Reclam. Univ. 2006, 18, 34–36. [Google Scholar]
- Zhang, J. Numerical Simulation and Experiment of Cranklink Organization Vibration Screener Based on Discrete Element Method. Bachelor’s Thesis, Northwest A & F University, Yangling, China, 2018. [Google Scholar]
- Xia, X.H.; Jin, W.M.; Zhang, Z.L. Simulation research, application status and development trend ofvibrating screen. J. Cent. South Univ. Sci. Technol. 2020, 51, 2689–2706. [Google Scholar]
- Wang, Z.H.; Wang, G.Y.; Liu, W.W. Present status and developing tendency of vibration screen. J. Shenyang Arch. Civ. Eng. Inst. 1999, 15, 78–82. [Google Scholar]
- Wang, L.J.; Li, R.; Yu, Y.T. Design and Test of Double-layer Non-parallel Vibrating Screens. J. Agric. Mach. 2019, 50, 130–139. [Google Scholar]
- Wang, L.J.; Duan, L.K.; Zheng, Z.H. Optimization and Experiment on Driving Mechanism of Vibrating Screen with Three Translations and Two Rotations. J. Agric. Mach. 2018, 49, 138–145. [Google Scholar]
- Xu, J.; Xiong, L.B.; Chen, P.L. The Design of a New Type Grain Lateral Vibration Plane Screen. Res. Agric. Mech. 2006, 110–111+114. [Google Scholar]
- Shen, D.C.; Hao, X.L.; Hu, D.S. The Considerable Problem When Design Oscillating Grain Pan. J. Jiamusi Inst. Technol. 1993, 11, 213–216. [Google Scholar]
- Yi, S.J.; Tao, G.X.; Mao, X. Comparative experiment on the distribution regularities of threshed mixtures for two types of axial flow threshing and separating installation. Trans. CSAE 2008, 24, 154–156. [Google Scholar]
- Geng, D.Y.; Zhang, D.L.; Wang, X.Y. New Agricultural Mechanics; Defense Industry Press: Beijing, China, 2011. [Google Scholar]
- Xu, X.H.; He, M.Z. Experimental Design with Design-Expert, SPSS Applications; Science Press: Beijing, China, 2010. [Google Scholar]
- Wang, Y.F.; Wang, C.G. The Application of Response Surface Methodology. J. CUN Nat. Sci. Ed. 2005, 14, 5. [Google Scholar]
- GB/T 21962-2020; Corn Combine Harvester. State Administration for Market Supervision and Administration, China National Standardization Administration: Beijing, China, 2020.

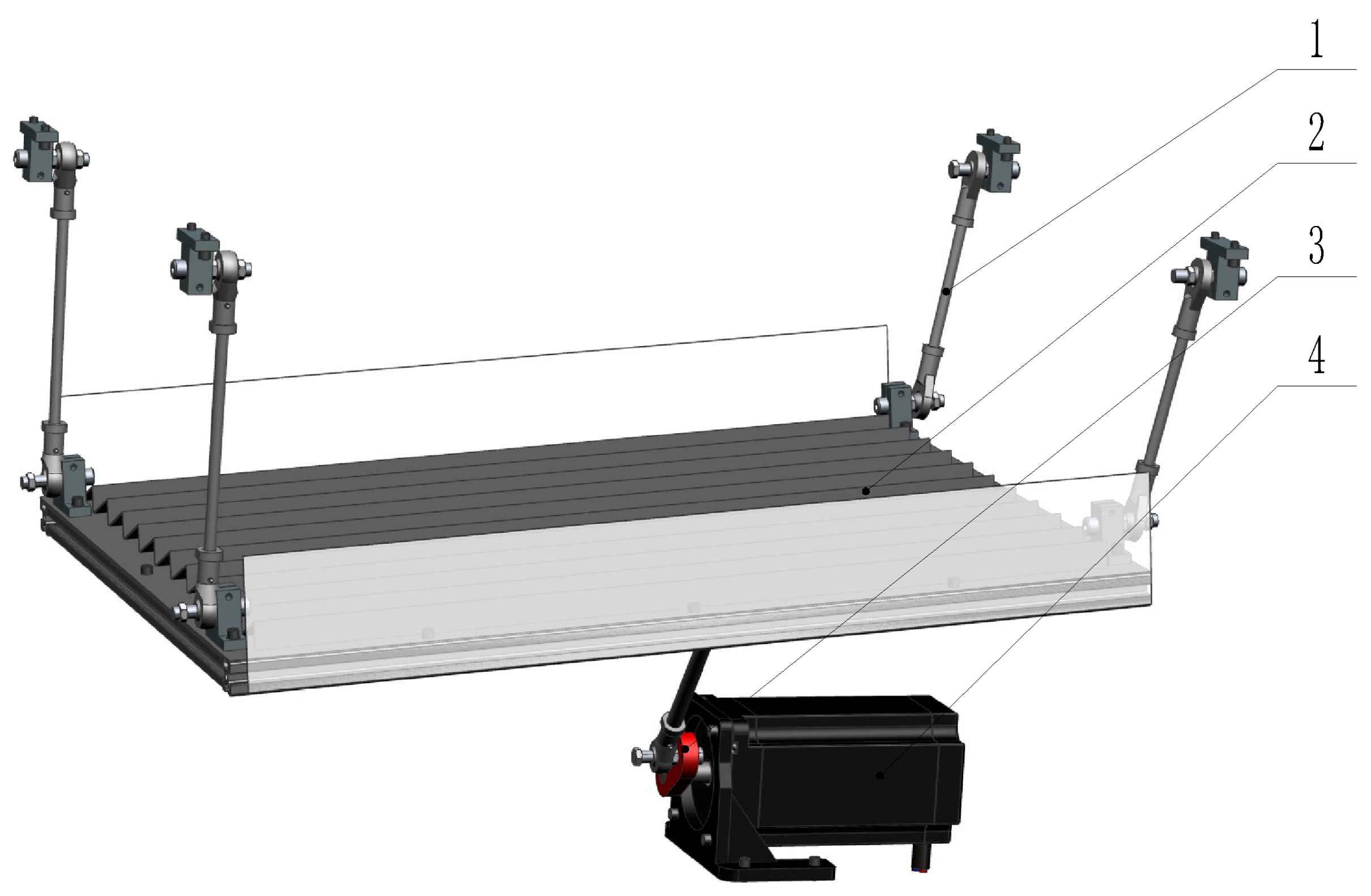


















| Contact Parameter | Coefficient of Restitution | Coefficient of Static Friction | Coefficient of Rolling Friction |
|---|---|---|---|
| Corn kernels/ corn kernels | 0.3 | 0.5 | 0.01 |
| Corn kernels/ step plates | 0.3 | 0.38 | 0.01 |
| Corn kernels/ step plates | 0.29 | 0.38 | 0.01 |
| Maize kernel/ cob | 0.2 | 0.6 | 0.01 |
| Corn kernels/ corn kernels | 0.3 | 0.7 | 0.01 |
| Materials | Sorghum | Step Plates |
|---|---|---|
| Poisson’s ratio | 0.3 | 0.24 |
| Shear modulus/Pa | 1.0 × 107 | 7.9 × 107 |
| Densities/kg·m−3 | 900 | 7850 |
| Column 1 | Column 2 | Column 3 | Column 4 | Column 5 | Column 6 | |
|---|---|---|---|---|---|---|
| Seed quality (g) | 506.8 | 352.4 | 204 | 167.2 | 183.2 | 203.2 |
| Rate of seed production (g/s) | 101.36 | 70.48 | 40.24 | 33.44 | 36.64 | 40.64 |
| Column 1 | Column 2 | Column 3 | Column 4 | Column 5 | Column 6 | |
|---|---|---|---|---|---|---|
| Trash mass (g) | 54.8 | 65.6 | 55.6 | 52.8 | 21.6 | 35.2 |
| Rate of generation of impurities (g/s) | 10.66 | 13.12 | 13.04 | 10.56 | 4.32 | 6.74 |
| Sports Event | Work Unit (One’s Workplace) | Parameters |
|---|---|---|
| L × W × H | mm | 1540 × 640 × 1000 |
| Motor power of cleaning sieve | KW | 2.2 |
| Motor power of reflux plate | KW | 3 |
| Cleaning sieve size | mm | 540 × 1200 |
| Reflux plate size | mm | 480 × 560 |
| Fan speed | r/min | 900~1500 |
| Dimensions of collection unit (L × W) | mm | 600 × 400 |
| Encodings | Factors | ||
|---|---|---|---|
| /° | /r/min | /mm | |
| −1 | 26 | 225 | 15 |
| 0 | 29 | 250 | 18 |
| 1 | 32 | 275 | 21 |
| Serial Number | Tilt Angle X1 | Motor Speed X2 | Amplification X3 | Seed Impurity Rate Y/% |
|---|---|---|---|---|
| 1 | −1 | −1 | 0 | 2.41 |
| 2 | 1 | −1 | 0 | 3.27 |
| 3 | −1 | 1 | 0 | 3.01 |
| 4 | 1 | 1 | 0 | 4.21 |
| 5 | −1 | 0 | −1 | 2.63 |
| 6 | 1 | 0 | −1 | 3.05 |
| 7 | −1 | 0 | 1 | 2.44 |
| 8 | 1 | 0 | 1 | 4.03 |
| 9 | 0 | −1 | −1 | 3.58 |
| 10 | 0 | 1 | −1 | 2.54 |
| 11 | 0 | −1 | 1 | 2.78 |
| 12 | 0 | 1 | 1 | 4.07 |
| 13 | 0 | 0 | 0 | 1.56 |
| 14 | 0 | 0 | 0 | 1.55 |
| 15 | 0 | 0 | 0 | 1.57 |
| 16 | 0 | 0 | 0 | 1.58 |
| 17 | 0 | 0 | 0 | 1.62 |
| Source of Variation | The Sum of the Squared Deviations from the Mean | (Number of) Degrees of Freedom | Mean Square | F | p |
|---|---|---|---|---|---|
| model | 13.63 | 9 | 1.51 | 49.3 | <0.0001 ** |
| 2.07 | 1 | 2.07 | 67.4 | <0.0001 ** | |
| 0.4 | 1 | 0.4 | 13.04 | 0.0086 ** | |
| 0.29 | 1 | 0.29 | 9.4 | 0.0182 * | |
| 3 × 10−2 | 1 | 3 × 10−2 | 0.94 | 0.3644 | |
| 0.34 | 1 | 0.34 | 11.14 | 0.0125 * | |
| 1 × 10−3 | 1 | 1.36 | 44.18 | 0.0003 ** | |
| 2.22 | 1 | 2.22 | 72.24 | <0.0001 ** | |
| 3.65 | 1 | 3.65 | 18.79 | <0.0001 ** | |
| 2.33 | 1 | 2.33 | 75.76 | <0.0001 ** | |
| residual | 0.22 | 7 | 3 × 10−2 | ||
| lost proposal | 0.21 | 3 | 0.07 | 44.33 | 0.0016 |
| pure error | 6 × 10−3 | 4 | 1.5 × 10−3 | ||
| inaccuracies | 13.85 | 16 |
| Serial Number | Seed Impurity (%) |
|---|---|
| 1 | 0.48 |
| 2 | 0.51 |
| 3 | 0.49 |
| 4 | 0.52 |
| 5 | 0.47 |
| 6 | 0.48 |
| Test Number | Original Program Impurity Rate (%) | Optimization Plan Impurity Rate (%) |
|---|---|---|
| 1 | 1.58 | 0.48 |
| 2 | 1.57 | 0.45 |
| 3 | 1.62 | 0.52 |
| average value | 1.59 | 0.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ming, J.; He, Q.; Yue, D.; Ma, J.; Wang, Y.; Yin, J.; Cui, Y.; Geng, D. Study and Experiment on Screen Surface Homogenization Technology of Dislodged Material Based on Longitudinal Flow Threshing. Agriculture 2024, 14, 731. https://doi.org/10.3390/agriculture14050731
Ming J, He Q, Yue D, Ma J, Wang Y, Yin J, Cui Y, Geng D. Study and Experiment on Screen Surface Homogenization Technology of Dislodged Material Based on Longitudinal Flow Threshing. Agriculture. 2024; 14(5):731. https://doi.org/10.3390/agriculture14050731
Chicago/Turabian StyleMing, Jiarui, Qinghao He, Dong Yue, Jie Ma, Yanan Wang, Jianning Yin, Yipeng Cui, and Duanyang Geng. 2024. "Study and Experiment on Screen Surface Homogenization Technology of Dislodged Material Based on Longitudinal Flow Threshing" Agriculture 14, no. 5: 731. https://doi.org/10.3390/agriculture14050731





