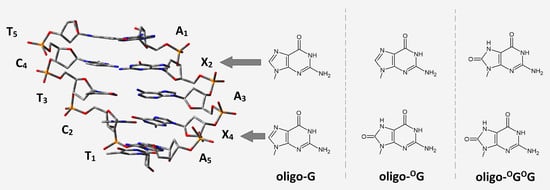
How Clustered DNA Damage Can Change the Electronic Properties of ds-DNA—Differences between GAG, GAOXOG, and OXOGAOXOG
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. The Structure Changes in the DNA Double Helix after Electron Loss or Extra Electron Adoption
3.2. The Oligo-G, Oligo-OG, and Oligo-OGOG Electronic Properties
3.3. Ds-DNA Changes in Charge, Spin, and HOMO–LUMO Distribution
3.4. A Comparison of the Electronic Properties of Individual Base Pairs within Oligo-G, Oligo-OG, and Oligo-OGOG
3.5. The Differences between Oligo-G, Oligo-OG, and Oligo-OGOG during Charge Migration through ds-DNA
3.6. The Rate Constant of Electron Hole and Excess Electron Transfer through Canonical and Lesioned ds-DNA
3.6.1. The Driving Force
3.6.2. Reorganization Energy
3.6.3. Activation Energy
3.6.4. The Charge Transfer Rate Constant
4. Discussion
- In the native oligo-G, the radical cation was located on the 5′-End guanine of the sequence d[A1G2A3G4A5]*d[T5C4T3C2T1], which is in good agreement with previous data. Moreover, in the initial vertical cation state (non-equilibrated solvent (NE) mode), the charge and spin were dispersed over both guanines with subsequent rearmament (equilibrated solvent—(EQ) mode) towards the 5′-end one. As expected, the G2C4 base pair becomes the final point of adiabatic radical formation. Contrary to that, the G4C2 was exclusively, in all cases, the point of excess electron accumulation. Moreover, the kHT of charge transfer through oligo-G showed that electron-hole migration is privileged towards G2C4, while the extra electron is in a G4C2 direction. Similar results were obtained from an analysis of energetic barriers.
- OXOG appearing in the double helix structure (oligo-OG) confirms previous theoretical and experimental observations. OXOG becomes the sink of the radical cation after one-electron ds-DNA oxidation. Moreover, irrespective of the radical cation’s state, i.e., vertical or adiabatic, and the solvent state—NE or EQ—the positive charge and spin were exclusively located on the OXOG. Additionally, analysis of the energetic barriers and charge rate constant disclosed the preference of electron-hole migration towards the OXOG position in ds-oligo.
- The analysis of clustered DNA damage containing two OXOGs separated by adenine showed opposite results to those found for the corresponding native oligo-G. The adiabatic ionization potential of this short oligo was found at the same level as that assigned for oligo-OG. Firstly, for the initial vertical cation state in the NE and EQ modes, the spin and positive charge were dispersed over three base pairs 5′-OXOGAOXOG-3′. The system relaxation (adiabatic state) led to spin and charge shift exclusively to the 3′-End OXOG, which is opposite to the results obtained for native oligo, in which spin and charge were located on the 5′-End guanine. Secondly, careful analysis of the adiabatic ionization potential of the base pairs present in oligo-OGOG showed that 5′-End OXOG2 possesses a higher AIP than G4 in oligo-G. This indicates that even the discussed oligo containing the symmetric sequence OXOGs are not equal in terms of electronic properties (OXOG2 ≠ OXOG4).
- A comparative analysis of the positive charge (hole) transfer rate constant (kHT) revealed a strong relationship to the spatial geometry changes of all the discussed ds-oligos (Table 4). The highest rate constants in (s−1) were notably found for A1T1→G2C2 and G2C2←A3T3 of oligo-G: 2.2 × 1012 and 1.5 × 1012, respectively. The presence of OXOdG in the oligo structure slows down the kHT as follows: A3T3→OXOG4C4 (1.0 × 109, 1.26 × 109), OXOG4C4←A5T5 (2.3 × 108, 5.15 × 107) of oligo-OG and oligo-OGOG, respectively. The obtained results indicate that OXOG can play a significant role in hole migration through the double helix, in light of its minimal influence on the spatial ds-DNA geometry.
- On the other hand, electron migration through stacked base pairs was found to be different for oligo-G, oligo-OG, and oligo-OGOG (Table 4). The kHT was found at a level of 1013–1015 (s−1) for base pair dimers of oligo-G. In the case of oligo-OG, a slowing down of up to 5.70 × 109 (s−1) of the A1T1→G2C2 electron transfer rate was determined for oligo-OG. The appearance of the second OXOG in the ds-oligo (oligo-OGOG) led to further kHT (s−1) decreases of the A1T1→OXOG2C2 (1.37 × 101) and OXOG2C2←A3T3 (5.32 × 104) steps, which indicates that even OXOG2 and OXOG4 are not equal in terms of electron transfer.
- At this point, it is important to mention that even a low dose of radiation at the level of 1 Gy can induce clustered lesions [1,52,53]; hence, it can be expected that tandem lesions such as cdPus can be induced too. CdPus are produced in anaerobic conditions and a hypoxia milieu, which is common for cancer cells, and favors the reaction of carbon-centred or peroxyl nucleotide radicals with the adjacent DNA part [54]. In medical treatment, the most frequent radiodiagnostic techniques use X-rays and gamma radiation, which are classified as Low-LET (Linear Energy Transfer) factors. For example, 131I (a gamma and beta emitter) is commonly used for thyroid therapy and diagnosis [55]. On the other hand, medical centers based on High-LET treatment are becoming of high interest in nuclear medicine–radiotherapy. Following Asaithamby, it can be concluded that High-LET has induced numerous incidents of chromosomal rearrangement [56]. As of 2020, almost 100 such centers exist in 30 countries, with 200,000 patients treated in the USA alone [57]. Therefore, it is important to know how the repair proteins of primary and pathologic/cancer cells recognise the local multiple-damaged sites (LMDS) composed of different kinds of DNA lesions and how LMDS attract repair proteins. For example, a DNA double-strand break (DSB) or an inter- or intrastrand cross-link are repaired by homologous recombination (HR) and nonhomologous end-joining (NHEJ) [58]. The above-mentioned repair mechanisms are already well recognised in the case of isolated lesions, while the recognition and repair process of clustered lesions still requires further advanced studies [59].
Supplementary Materials
Funding
Conflicts of Interest
References
- Evans, M.D.; Dizdaroglu, M.; Cooke, M.S. Oxidative DNA Damage and Disease: Induction, Repair and Significance. Mutat. Res. 2004, 567, 1–61. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsova, A.A.; Knorre, D.G.; Fedorova, O.S. Oxidation of DNA and its components with reactive oxygen species. Russ. Chem. Rev. 2009, 78, 659–678. [Google Scholar] [CrossRef]
- Shukla, L.I.; Adhikary, A.; Pazdro, R.; Becker, D.; Sevilla, M.D. Formation of 8-oxo-7,8-dihydroguanine-radicals in γ-irradiated DNA by multiple one-electron oxidations. Nucleic Acids Res. 2004, 32, 6565–6574. [Google Scholar] [CrossRef] [PubMed]
- Kanvah, S.; Schuster, G.B. Long-range oxidative damage to DNA: Protection of guanines by a nonspecifically bound disulfide. J. Am. Chem. Soc. 2002, 124, 11286–11287. [Google Scholar] [CrossRef] [PubMed]
- Sugiyama, H.; Saito, I. Theoretical studies of GG-specific photocleavage of DNA via electron transfer: Significant lowering of ionization potential and 5′-localization of HOMO of stacked GG bases in B-form DNA. J. Am. Chem. Soc. 1996, 118, 7063–7068. [Google Scholar] [CrossRef]
- Voityuk, A.A.; Jortner, J.; Bixon, M.; Rösch, N. Energetics of hole transfer in DNA. Chem. Phys. Lett. 2000, 324, 430–434. [Google Scholar] [CrossRef]
- Senthilkumar, K.; Grozema, F.C.; Guerra, C.F.; Bickelhaupt, F.M.; Siebbeles, L.D.A. Mapping the Sites for Selective Oxidation of Guanines in DNA. J. Am. Chem. Soc. 2003, 125, 13658–13659. [Google Scholar] [CrossRef]
- Taggart, D.J.; Fredrickson, S.W.; Gadkari, V.V.; Suo, Z. Mutagenic potential of 8-oxo-7,8-dihydro-2′-deoxyguanosine bypass catalyzed by human Y-family DNA polymerases. Chem. Res. Toxicol. 2014, 27, 931–940. [Google Scholar] [CrossRef] [PubMed]
- Kairupan, C.; Scott, R.J. Base excision repair and the role of MUTYH. Hered. Cancer Clin. Pract. 2007, 5, 199–209. [Google Scholar] [CrossRef] [Green Version]
- Boal, A.K.; Genereux, J.C.; Sontz, P.A.; Gralnick, J.A.; Newman, D.K.; Barton, J.K. Redox signaling between DNA repair proteins for efficient lesion detection. Proc. Natl. Acad. Sci. USA 2009, 106, 15237–15242. [Google Scholar] [CrossRef] [Green Version]
- Bignon, E.; Gattuso, H.; Morell, C.; Dehez, F.; Georgakilas, A.G.; Monari, A.; Dumont, E. Correlation of bistranded clustered abasic DNA lesion processing with structural and dynamic DNA helix distortion. Nucleic Acids Res. 2016, 44, 8588–8599. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karwowski, B.; Guga, P.; Kobylańska, A.; Stec, W.J. Nucleoside 3′-O-(2-oxo-′spiro′-4.4-pentamethylene-1.3.2-oxathiaphospholane)s: Monomers for stereocontrolled synthesis of oligo(nucleoside phosphorothioate/phosphate)s. Nucleosides Nucleotides 1998, 17, 1747–1759. [Google Scholar] [CrossRef]
- Plumley, J.A.; Dannenberg, J.J. A comparison of the behavior of functional/basis set combinations for hydrogen-bonding in the water dimer with emphasis on basis set superposition error. J. Comput. Chem. 2011, 32, 1519–1527. [Google Scholar] [CrossRef]
- Zhao, Y.; Pu, J.; Lynch, B.J.; Truhlar, D.G. Tests of second-generation and third-generation density functionals for thermochemical kinetics. Electronic supplementary information (ESI) available: Mean errors for pure and hybrid DFT methods. See http://www.rsc.org/suppdata/cp/b3/b316260e/. Phys. Chem. Chem. Phys. 2004, 6, 673. [Google Scholar] [CrossRef]
- Dapprich, S.; Komáromi, I.; Byun, K.S.; Morokuma, K.; Frisch, M.J. A new ONIOM implementation in Gaussian98. Part I. The calculation of energies, gradients, vibrational frequencies and electric field derivatives. J. Mol. Struct. THEOCHEM 1999, 461–462, 1–21. [Google Scholar] [CrossRef]
- Cammi, R.; Corni, S.; Mennucci, B.; Tomasi, J. Electronic excitation energies of molecules in solution: State specific and linear response methods for nonequilibrium continuum solvation models. J. Chem. Phys. 2005, 122, 104513. [Google Scholar] [CrossRef]
- Gu, J.; Wang, J.; Leszczynski, J. Electron attachment-induced DNA single-strand breaks at the pyrimidine sites. Nucleic Acids Res. 2010, 38, 5280–5290. [Google Scholar] [CrossRef] [Green Version]
- Hirshfeld, F.L. Bonded-atom fragments for describing molecular charge densities. Theor. Chim. Acta 1977, 44, 129–138. [Google Scholar] [CrossRef]
- Karwowski, B.T. Ionisation potential and electron affinity of free 5′,8-cyclopurine-2′-deoxynucleosides. DFT study in gaseous and aqueous phase. Cent. Eur. J. Chem. 2010, 8, 70–76. [Google Scholar] [CrossRef]
- Li, T.C.; Tong, P.Q. Time-dependent density-functional theory for multicomponent systems. Phys. Rev. A 1986, 34, 529–532. [Google Scholar] [CrossRef]
- Cave, R.J.; Newton, M.D. Generalization of the Mulliken-Hush treatment for the calculation of electron transfer matrix elements. Chem. Phys. Lett. 1996, 249, 15–19. [Google Scholar] [CrossRef]
- Miertusš, S.; Tomasi, J. Approximate evaluations of the electrostatic free energy and internal energy changes in solution processes. Chem. Phys. 1982, 65, 239–245. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 16, Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2019; Volume 2019, p. 2019. [Google Scholar]
- Manlove, A.H.; McKibbin, P.L.; Doyle, E.L.; Majumdar, C.; Hamm, M.L.; David, S.S. Structure-Activity Relationships Reveal Key Features of 8-Oxoguanine: A Mismatch Detection by the MutY Glycosylase. ACS Chem. Biol. 2017, 12, 2335–2344. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boal, A.K.; Yavin, E.; Lukianova, O.A.; O’Shea, V.L.; David, S.S.; Barton, J.K. DNA-bound redox activity of DNA repair glycosylases containing [4Fe-4S] clusters. Biochemistry 2005, 44, 8397–8407. [Google Scholar] [CrossRef] [PubMed]
- Núñez, M.E.; Hall, D.B.; Barton, J.K. Long-range oxidative damage to DNA: Effects of distance and sequence. Chem. Biol. 1999, 6, 85–97. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Adhikary, A.; Kumar, A.; Munafo, S.A.; Khanduri, D.; Sevilla, M.D. Prototropic equilibria in DNA containing one-electron oxidized GC: Intra-duplex vs. duplex to solvent deprotonation. Phys. Chem. Chem. Phys. 2010, 12, 5353–5368. [Google Scholar] [CrossRef] [Green Version]
- Giese, B. LONG-DISTANCEE LECTRON TRANSFER THROUGH DNA. Annu. Rev. Biochem. 2002, 71, 51–70. [Google Scholar] [CrossRef]
- Genereux, J.C.; Barton, J.K. Mechanism for DNA charge transfer. Chem Rev. 2010, 110, 1642–1662. [Google Scholar] [CrossRef] [Green Version]
- Breslin, D.T.; Schuster, G.B. Anthraquinone photonucleases: Mechanisms for GG-selective and nonselective cleavage of double-stranded DNA. J. Am. Chem. Soc. 1996, 118, 554–558. [Google Scholar] [CrossRef]
- Kumar, A.; Adhikary, A.; Sevilla, M.D.; Close, D.M. One-electron oxidation of ds(5′-GGG-3′) and ds(5′-G(8OG)G-3′) and the nature of hole distribution: A density functional theory (DFT) study. Phys. Chem. Chem. Phys. 2020, 22, 5078–5089. [Google Scholar] [CrossRef]
- Jalbout, A.F.; Adamowicz, L. Electron Attachment to DNA Base Complexes. Adv. Quantum Chem. 2007, 52, 231–251. [Google Scholar] [CrossRef]
- Steenken, S.; Jovanovic, S.V.; Bietti, M.; Bernhard, K. The trap depth (in DNA) of 8-oxo-7,8-dihydro-2′deoxyguanosine as derived from electron-transfer equilibria in aqueous solution [2]. J. Am. Chem. Soc. 2000, 122, 2373–2374. [Google Scholar] [CrossRef]
- Amati, M.; Stoia, S.; Baerends, E.J. The Electron Affinity as the Highest Occupied Anion Orbital Energy with a Sufficiently Accurate Approximation of the Exact Kohn-Sham Potential. J. Chem. Theory Comput. 2020, 16, 443–452. [Google Scholar] [CrossRef] [Green Version]
- Kumar, A.; Sevilla, M.D. Theoretical Modeling of Radiation-Induced DNA Damage. In Radical and Radical Ion Reactivity in Nucleic Acid Chemistry; John Wiley & Sons: Hoboken, NJ, USA, 2009; pp. 1–40. [Google Scholar] [CrossRef] [Green Version]
- Diamantis, P.; Tavernelli, I.; Rothlisberger, U. Redox Properties of Native and Damaged DNA from Mixed Quantum Mechanical/Molecular Mechanics Molecular Dynamics Simulations. J. Chem. Theory Comput. 2020, 16, 6690–6701. [Google Scholar] [CrossRef]
- Diamantis, P.; Tavernelli, I.; Rothlisberger, U. Vertical Ionization Energies and Electron Affinities of Native and Damaged DNA Bases, Nucleotides, and Pairs from Density Functional Theory Calculations: Model Assessment and Implications for DNA Damage Recognition and Repair. J. Chem. Theory Comput. 2019, 15, 2042–2052. [Google Scholar] [CrossRef] [PubMed]
- Albiser, G.; Lamiri, A.; Premilat, S. The A-B transition: Temperature and base composition effects on hydration of DNA. Int. J. Biol. Macromol. 2001, 28, 199–203. [Google Scholar] [CrossRef] [PubMed]
- Kanvah, S.; Schuster, G.B. Oxidative damage to DNA: Inhibition of guanine damage. Pure Appl. Chem. 2006, 78, 2297–2304. [Google Scholar] [CrossRef] [Green Version]
- Adhikary, A.; Khanduri, D.; Sevilla, M.D. Direct observation of the hole protonation state and hole localization site in DNA-oligomers. J. Am. Chem. Soc. 2009, 131, 8614–8619. [Google Scholar] [CrossRef] [Green Version]
- Coolidge, A.S.; James, H.M.; Present, R.D. A study of the franck-condon principle. J. Chem. Phys. 1936, 4, 193–211. [Google Scholar] [CrossRef]
- Elias, B.; Shao, F.; Barton, J.K. Charge migration along the DNA duplex: Hole versus electron transport. J. Am. Chem. Soc. 2008, 130, 1152–1153. [Google Scholar] [CrossRef]
- Rawtani, D.; Kuntmal, B.; Agrawal, Y. Charge transfer in DNA and its diverse modelling approaches. Front. Life Sci. 2016, 9, 214–225. [Google Scholar] [CrossRef] [Green Version]
- Steenken, S.; Jovanovic, S.V. How easily oxidizable is DNA? One-electron reduction potentials of adenosine and guanosine radicals in aqueous solution. J. Am. Chem. Soc. 1997, 119, 617–618. [Google Scholar] [CrossRef]
- Takada, T.; Kawai, K.; Fujitsuka, M.; Majima, T. Direct observation of hole transfer through double-helical DNA over 100 Å. Proc. Natl. Acad. Sci. USA 2004, 101, 14002–14006. [Google Scholar] [CrossRef] [Green Version]
- Kumpulainen, T.; Lang, B.; Rosspeintner, A.; Vauthey, E. Ultrafast Elementary Photochemical Processes of Organic Molecules in Liquid Solution. Chem. Rev. 2017, 117, 10826–10939. [Google Scholar] [CrossRef] [PubMed]
- Fujitsuka, M.; Majima, T. Charge transfer in DNA *. Pure Appl. Chem. 2013, 85, 1367–1377. [Google Scholar] [CrossRef] [Green Version]
- Bolton, J.R.; Archer, M.D. Basic Electron-Transfer Theory. Electron. Transf. Inorg. Org. Biol. Syst. 1991, 228, 7–23. [Google Scholar]
- Cadet, J.; Richard Wagner, J. DNA base damage by reactive oxygen species, oxidizing agents, and UV radiation. Cold Spring Harb. Perspect. Biol. 2013, 5, a012559. [Google Scholar] [CrossRef]
- Lakhno, V.D. On the possibility of nonexponential dependence of electron transfer in DNA. Dokl. Akad. Nauk 2000, 371, 255–257. [Google Scholar]
- Karwowski, B.T. The AT Interstrand Cross-Link: Structure, Electronic Properties, and Influence on Charge Transfer in dsDNA. Mol. Ther. Nucleic Acids 2018, 13, 665–685. [Google Scholar] [CrossRef] [Green Version]
- Arnold, A.R.; Grodick, M.A.; Barton, J.K. Review DNA Charge Transport: From Chemical Principles to the Cell. Cell Chem. Biol. 2016, 23, 183–197. [Google Scholar] [CrossRef] [Green Version]
- Goodhead, D.T. Initial events in the cellular effects of ionizing radiations: Clustered damage in DNA. Int. J. Radiat. Biol. 1994, 65, 7–17. [Google Scholar] [CrossRef] [PubMed]
- Greenberg, M.M. Tandem and clustered lesions from radicals in nucleic acids from a single initial chemical event. In DNA Damage, DNA Repair and Disease; Dizdaroglu, M., Lloyd, R., Eds.; The Royal Society of Chemistry: Cambridge, UK, 2021; Volume 1, pp. 27–61. [Google Scholar]
- Adamczewski, Z.; Stasio, M.; Dedecjus, M. The Effect of Diagnostic Absorbed Doses from 131 I on Human Thyrocytes In Vitro. Int. J. Mol. Sci. 2015, 16, 14608–14622. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Asaithamby, A.; Hu, B.; Chen, D.J. Unrepaired clustered DNA lesions induce chromosome breakage in human cells. Proc. Natl. Acad. Sci. USA 2011, 108, 8293–8298. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global Cancer Statistics 2020: GLOBOCAN Estimates of Incidence and Mortality Worldwide for 36 Cancers in 185 Countries. CA A Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef]
- Chiruvella, K.K.; Liang, Z.; Wilson, T.E. Repair of double-strand breaks by end joining. Cold Spring Harb. Perspect. Biol. 2013, 5, a012757. [Google Scholar] [CrossRef] [PubMed]
- Lomax, M.E.; Folkes, L.K.; O’Neill, P. Biological consequences of radiation-induced DNA damage: Relevance to radiotherapy. Clin. Oncol. 2013, 25, 578–585. [Google Scholar] [CrossRef] [Green Version]
- Rösch, N.; Voityuk, A.A. Quantum Chemical Calculation of Donor–Acceptor Coupling for Charge Transfer in DNA. Long-Range Charg. Transf. DNA II 2012, 237, 37–72. [Google Scholar] [CrossRef]
- Takada, T.; Kawai, K.; Fujitsuka, M.; Majima, T. Contributions of the distance-dependent reorganization energy and proton-transfer to the hole-transfer process in DNA. Chem.—A Eur. J. 2005, 11, 3835–3842. [Google Scholar] [CrossRef]
- Grodick, M.A.; Muren, N.B.; Barton, J.K. DNA Charge Transport within the Cell. Biochemistry 2015, 54, 962–973. [Google Scholar] [CrossRef] [Green Version]
- Dršata, T.; Kara, M.; Zacharias, M.; Lankaš, F. Effect of 8-oxoguanine on DNA structure and deformability. J. Phys. Chem. B 2013, 117, 11617–11622. [Google Scholar] [CrossRef]
- Schuster, G.B. Long-range charge transfer in DNA: Transient structural distortions control the distance dependence. Acc. Chem. Res. 2000, 33, 253–260. [Google Scholar] [CrossRef] [PubMed]
- Sontz, P.A.; Muren, N.B.; Barton, J.K. DNA charge transport for sensing and signaling. Acc. Chem. Res. 2012, 45, 1792–1800. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rajski, S.R.; Jackson, B.A.; Barton, J.K. DNA repair: Models for damage and mismatch recognition. Mutat. Res. Fundam. Mol. Mech. Mutagen. 2000, 447, 49–72. [Google Scholar] [CrossRef] [PubMed]
- Tse, E.C.M.; Zwang, T.J.; Bedoya, S.; Barton, J.K. Effective Distance for DNA-Mediated Charge Transport between Repair Proteins. ACS Cent. Sci. 2019, 5, 65–72. [Google Scholar] [CrossRef] [Green Version]





| System Overlap | RMSD [Å2] | |||
|---|---|---|---|---|
| ds-Oligonucleotides | ||||
| Oligo-G | Oligo-OG | Oligo-OGOG | ||
| Anion vs. Neutral | ds-DNA | 0.17 | 0.13 | 0.11 |
| Base Pairs | 0.16 | 0.12 | 0.11 | |
| SP-backbone | 0.17 | 0.15 | 0.12 | |
| Cation vs. Neutral | ds-DNA | 0.36 | 0.31 | 0.34 |
| Base Pairs | 0.31 | 0.23 | 0.29 | |
| SP-backbone | 0.42 | 0.38 | 0.37 | |
| Parameter | ds-Oligonucleotides | |||||
|---|---|---|---|---|---|---|
| Oligo-G | Oligo-OG | Oligo-OGOG | ||||
| ds-DNA | BP-System | ds-DNA | BP-System | ds-DNA | BP-System | |
| VIPNE | 6.72 | 6.48 | 6.49 | 6.27 | 6.54 | 6.34 |
| VIPEQ | 6.08 | 5.98 | 5.86 | 5.79 | 6.02 | 5.99 |
| AIP | 5.65 | 5.58 | 5.39 | 5.38 | 5.39 | 5.40 |
| VEAENE | 4.61 | 4.85 | 4.40 | 4.91 | −4.40 | −4.71 |
| VEAEEQ | 5.26 | 5.19 | 5.04 | 4.98 | −5.04 | −4.99 |
| VEANE | −0.84 | −0.60 | −0.85 | −0.60 | −0.86 | −0.62 |
| VEAEQ | −1.58 | −1.34 | −1.43 | −1.35 | −1.59 | −1.39 |
| AEA | −2.09 | −1.90 | −2.04 | −1.90 | −2.09 | −1.90 |
| VEDENE | 3.36 | 2.56 | 3.36 | 2.62 | 3.37 | 2.65 |
| VEDEEQ | 2.66 | 2.48 | 2.67 | 2.48 | 2.68 | 2.49 |
| Oligo-G | Oligo-OG | Oligo-OGOG | |||||||
|---|---|---|---|---|---|---|---|---|---|
| X2,4:G | X2:G; X4:OXOG | X2,4:OXOG | |||||||
| VIP | AIP | VEAE | VIP | AIP | VEAE | VIP | AIP | VEAE | |
| A1T5 | 6.65 | 6.60 | −6.60 | 6.63 | 6.62 | −6.62 | 6.65 | 6.63 | −6.63 |
| X2C4 | 6.13 | 5.83 | −5.51 | 6.17 | 6.16 | −6.16 | 5.93 | 5.93 | −5.93 |
| A3T3 | 6.65 | 6.60 | −6.60 | 6.66 | 6.65 | −6.65 | 6.65 | 6.65 | −6.65 |
| X4C2 | 6.13 | 6.11 | −6.11 | 5.91 | 5.56 | −5.21 | 5.91 | 5.56 | −5.20 |
| A5T1 | 6.74 | 6.72 | −6.73 | 6.73 | 6.68 | −6.68 | 6.73 | 6.68 | −6.68 |
| VEA | AEA | VEDE | VEA | AEA | VEDE | VEA | AEA | VEDE | |
| A1T5 | −1.41 | −1.42 | 1.42 | −1.43 | −1.43 | 1.43 | −1.42 | −1.42 | 1.43 |
| X2C4 | −1.49 | −1.47 | 1.50 | −1.49 | −1.50 | 1.50 | −1.51 | −1.51 | 1.52 |
| A3T3 | −1.40 | −1.40 | 1.40 | −1.39 | −1.39 | 1.39 | −1.39 | −1.39 | 1.39 |
| X4C2 | −1.52 | −1.95 | 2.47 | −1.53 | −1.97 | 2.50 | −1.53 | −1.97 | 2.50 |
| A5T1 | −1.42 | −1.39 | 1.42 | −1.43 | −1.40 | 1.42 | −1.43 | −1.40 | 1.43 |
| Electron Transfer | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Oligo-G | Oligo-OG | ||||||||||
| System | λ | ΔG | Ea | V12 | kHT | System | λ | ΔG | Ea | V12 | kHT |
| A1T1→G2C2 | −0.02 | −0.05 | −0.06 | 0.02 | 0.00 | A1T1→G2C2 | 0.01 | −0.07 | 0.21 | 0.01 | 5.70 × 109 |
| G2C2←A3T3 | −0.02 | −0.07 | −0.11 | 0.04 | 0.00 | G2C2←A3T3 | 0.00 | −0.10 | −8.25 | 0.05 | 0.00 |
| A3T3→G4C4 | 0.43 | −0.54 | 0.01 | 0.07 | 8.75 × 1013 | A3T3→OG4C4 | 0.43 | −0.57 | 0.01 | 0.06 | 6.40 × 1013 |
| G4C4←A5T5 | 0.46 | −0.55 | 0.01 | 0.04 | 4.04 × 1013 | OG4C4←A5T5 | 0.45 | −0.56 | 0.01 | 0.04 | 3.05 × 1013 |
| A1T1←A3T3 | 0.01 | −0.02 | 0.004 | 0.09 | 1.2 × 1015 | A1T1←A3T3 | 3 × 10−3 | −0.03 | 0.09 | 0.09 | 6.9 × 1013 |
| G2C2→G4C4 | 0.46 | −0.47 | 0.00 | 0.05 | 4.9 × 1013 | G2C2→OG4C4 | 0.43 | −0.47 | 0.001 | 0.05 | 6.2 × 1013 |
| A3T5←A5T5 | −0.02 | −0.01 | −0.01 | 0.08 | 0.00 | A3T5→A5T5 | −0.03 | −0.01 | −0.01 | 0.08 | 0.00 |
| oligo−OGOG | 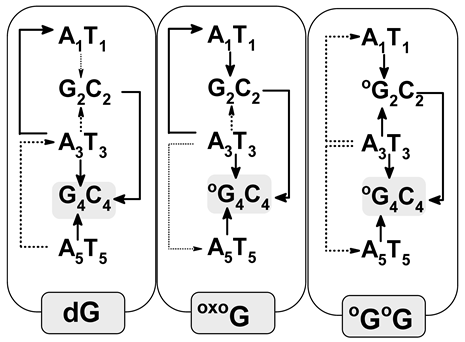 | ||||||||||
| A1T1→OG2C2 | 2.2 × 10−3 | −0.08 | 0.75 | 0.01 | 1.37 × 101 | ||||||
| OG2C2←A3T3 | 0.01 | −0.12 | 0.60 | 0.06 | 5.32 × 104 | ||||||
| A3T3→OG4C4 | 0.44 | −0.58 | 0.01 | 0.07 | 7.41 × 1013 | ||||||
| OG4C4←A5T5 | 0.45 | −0.56 | 0.01 | 0.05 | 4.28 × 1013 | ||||||
| A1T1←A3T3 | −2.5 × 10−3 | −0.04 | −0.17 | 0.02 | 0.00 | ||||||
| G2C2→OG4C4 | 0.44 | −0.46 | 2.0 × 10−4 | 0.05 | 6.87 × 1013 | ||||||
| A3T5→A5T5 | −0.02 | −0.02 | −0.02 | 0.07 | 0.00 | ||||||
| Hole Transfer | |||||||||||
| oligo-G | oligo-OG | ||||||||||
| System | λ | ΔG | Ea | V12 | kHT | System | λ | ΔG | Ea | V12 | kHT |
| A1T1→G2C2 | 0.30 | −0.77 | 0.18 | 0.30 | 2.2 × 1012 | A1T1→G2C2 | 0.00 | −0.46 | 11.08 | 0.29 | 0.00 |
| G2C2←A3T3 | 0.30 | −0.77 | 0.18 | 0.24 | 1.5 × 1012 | G2C2←A3T3 | 0.01 | −0.49 | 8.29 | 0.23 | 0.00 |
| A3T3→G4C4 | 0.03 | −0.49 | 2.05 | 0.28 | 0.00 | A3T3→OG4C4 | 0.35 | −1.09 | 0.40 | 0.41 | 1.0 × 109 |
| G4C4←A5T5 | 0.01 | −0.61 | 7.69 | 0.29 | 0.00 | OG4C4←A5T5 | 0.34 | −1.12 | 0.44 | 0.35 | 2.3 × 108 |
| A1T1←A3T3 | 0.05 | −0.00 | 0.01 | 0.02 | 2.1 × 1011 | A1T1←A3T3 | 0.01 | −0.03 | 0.01 | 0.01 | 1.4 × 1013 |
| G2C2←G4C4 | 0.29 | −0.28 | 2.0 × 10−4 | 0.01 | 3.6 × 1010 | G2C2→OG4C4 | 0.35 | −0.60 | 0.05 | 0.12 | 7.5 × 1013 |
| A3T3←A5T5 | 0.05 | −0.12 | 0.02 | 0.04 | 6.2 × 1013 | A3T3←A5T5 | 0.01 | −0.02 | 0.003 | 0.04 | 1.9 × 1014 |
| oligo-OGOG |  | ||||||||||
| A1T1→OG2C2 | −5.0 × 10−5 | −0.69 | −2.2 × 103 | 0.39 | 0.00 | ||||||
| OG2C2←A3T3 | 1.7 × 10−4 | −0.72 | 76.06 | 0.35 | 0.00 | ||||||
| A3T3→OG 4C4 | 0.35 | −1.09 | 0.39 | 0.41 | 1.26 × 109 | ||||||
| OG4C4←A5T5 | 0.35 | −1.12 | 0.42 | 0.16 | 5.15 × 107 | ||||||
| A1T1←A3T3 | 0.02 | −0.03 | 2.0 × 10−4 | 0.30 | 1.03 × 1016 | ||||||
| OG2C→OG 4C4 | 0.35 | −0.38 | 3.6 × 10−4 | 0.01 | 4.07 × 1012 | ||||||
| A3T5→A5T5 | −0.02 | −0.017 | −0.02 | 0.07 | 0.00 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karwowski, B. How Clustered DNA Damage Can Change the Electronic Properties of ds-DNA—Differences between GAG, GAOXOG, and OXOGAOXOG. Biomolecules 2023, 13, 517. https://doi.org/10.3390/biom13030517
Karwowski B. How Clustered DNA Damage Can Change the Electronic Properties of ds-DNA—Differences between GAG, GAOXOG, and OXOGAOXOG. Biomolecules. 2023; 13(3):517. https://doi.org/10.3390/biom13030517
Chicago/Turabian StyleKarwowski, Boleslaw. 2023. "How Clustered DNA Damage Can Change the Electronic Properties of ds-DNA—Differences between GAG, GAOXOG, and OXOGAOXOG" Biomolecules 13, no. 3: 517. https://doi.org/10.3390/biom13030517