Lean-and-Green Strength Performance Optimization of a Tube-to-Tubesheet Joint for a Shell-and-Tube Heat Exchanger Using Taguchi Methods and Random Forests
Abstract
:1. Introduction
2. Materials and Methods
2.1. Designing the Experiments
2.2. Test Tubesheet and Tube Specimens
2.3. CNC Machining of the Test Tubesheet Specimens
- 1.
- DIJET Drill Bit Inserts (No. TEZ1900, Osaka, Japan): a carbide tool material with PVD coating (JC8050). Two indexable drill-bit inserts, with nominal diameter of 19 mm (Figure 5a), were utilized.They were attached to a drill-body tool-holder (DIJET Drill Body, No. TEZD1900S25-MS). Each drill-bit insert was paired to complete each replicate set of nine workpieces as a preventive measure to curtail interloping variability due to local cutting process flaws.
- 2.
- Sandvik Coromant Boring Inserts (ANSI code: TCGX 1.8 (1.5) 1L-WK 5015, Sandvik Coromant, Sandviken, Sweden): an uncoated carbide tool material. Two indexable boring inserts were utilized with corner radius and thickness dimensions of 0.3969 mm and 2.3812 mm, respectively. They were attached to a boring tool-holder (Sandvik Coromant Boring Bar, ANSI code: CXS-10-17 050TC09) and were mounted to a fine boring head adapter with a nominal accuracy of 0.002 mm (Figure 5b). Each boring insert was paired to process each replicate set of nine workpieces, again as a simple preventive measure in minimizing variability due to cutting process flaws.
- 3.
- UOP T-slot Milling Cutters: solid High-Speed Steel (HSS) tool material (Roncadelle, Brescia, Italy). Two solid HSS T-slot milling cutters (Figure 5c), with cutting diameter and depth dimensions of 16.5 mm and 3 mm, respectively, were also outfitted with eight flutes. They were utilized to etch internal annular grooves on the tubesheet hole surfaces. Each T-slot milling cutter was paired to each separate set of nine workpieces. Upon completion of the machining process, the tubesheet specimens were crafted as shown in Figure 5d.
2.4. The Tube Expansion Process
2.4.1. Tube Expanding Machine and Tube Expander Tool
- A Matex tsx digital controller.
- A F/308-2 telescopic shaft which transmitted the rotational motion between the electric motor and the tube expander.
- An electric rolling motor (Matex R V4) which was composed of a brushless electric motor, and it was coupled to a mechanical gearbox with four speed options, i.e., 200, 300, 540, and 800 rpm.
- A PE900 foot switch control.
| Experiment No. | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| Tubesheet Hole ID (mm) | Tube OD (mm) | Clearance (A Minus B) (mm) | Tube ID (mm) | Tube ID at Metal-To-Metal contact (D Plus C) (mm) | Tube Wall Thickness Reduction (%) | Expanded Tube ID [F% of (B-D) Plus E] (mm) | |
| 1.1 | 19.10 | 18.99 | 0.11 | 14.97 | 15.08 | 4 | 15.24 |
| 1.2 | 19.10 | 19.00 | 0.10 | 14.96 | 15.06 | 4 | 15.22 |
| 2.1 | 19.08 | 19.01 | 0.07 | 14.98 | 15.05 | 8 | 15.37 |
| 2.2 | 19.10 | 19.02 | 0.08 | 14.96 | 15.04 | 8 | 15.36 |
| 3.1 | 19.10 | 18.99 | 0.11 | 14.97 | 15.08 | 12 | 15.56 |
| 3.2 | 19.09 | 19.03 | 0.06 | 14.97 | 15.03 | 12 | 15.52 |
| 4.1 | 19.24 | 19.01 | 0.23 | 14.97 | 15.20 | 12 | 15.68 |
| 4.2 | 19.24 | 19.00 | 0.24 | 14.98 | 15.22 | 12 | 15.70 |
| 5.1 | 19.24 | 19.02 | 0.22 | 14.96 | 15.18 | 4 | 15.34 |
| 5.2 | 19.25 | 19.01 | 0.24 | 14.97 | 15.21 | 4 | 15.37 |
| 6.1 | 19.24 | 19.02 | 0.22 | 14.98 | 15.20 | 8 | 15.52 |
| 6.2 | 19.25 | 19.00 | 0.25 | 14.96 | 15.21 | 8 | 15.53 |
| 7.1 | 19.39 | 19.00 | 0.39 | 14.96 | 15.35 | 8 | 15.67 |
| 7.2 | 19.40 | 19.01 | 0.39 | 14.97 | 15.36 | 8 | 15.68 |
| 8.1 | 19.41 | 19.02 | 0.39 | 14.96 | 15.35 | 12 | 15.84 |
| 8.2 | 19.40 | 19.00 | 0.40 | 14.97 | 15.37 | 12 | 15.85 |
| 9.1 | 19.40 | 18.99 | 0.41 | 14.97 | 15.38 | 4 | 15.54 |
| 9.2 | 19.40 | 19.00 | 0.40 | 14.96 | 15.36 | 4 | 15.52 |
2.4.2. Determination of the Proper Expanded Tube Inner Diameter
2.5. Joint Strength Measurements
2.6. Theoretical Aspects and Computational Aids
3. Results
3.1. Joint Strength Statistical Analysis Using Response Graphs and Tables
3.2. Proposed Optimal Solution for the Screening/Optimization of the Joint Strength
- Tube wall thickness reduction at level 3 (12%).
- Number of grooves at level 3 (Three).
- Groove depth at level 2 (0.40 ± 0.02 mm).
- Clearance at level 1 (0.10 ± 0.02 mm).
3.3. Confirmation Run for the Optimal Parameter Settings
4. Discussion
5. Conclusions
- Tube wall thickness reduction at level 3 (12%).
- Number of grooves at level 3 (Three).
- Groove depth at level 2 (0.40 mm).
- Clearance at level 1 (0.10 mm).
- Further testing would be informative in investigating the joint leakage by exposing the joint in either pneumatic or hydraulic pressure tests; joint leak tightness cannot be measured directly by push-out testing.
- Further testing is needed to be conducted to study the influence of surface finish of the tubesheet holes on joint strength and joint leak tightness.
- The effect of a five-roller tube expander and a tube expander which incorporates three expansion rollers with three flare rollers on joint strength and joint leak tightness would be beneficial.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nemati, H.; Ardekani, M.M.; Mahootchi, J.; Meyer, J.P. Fundamentals of Industrial Heat Exchangers: Selection, Design, Construction, and Operation; Elsevier: Amsterdam, The Netherlands, 2023. [Google Scholar]
- Nitsche, M.; Gbadamosi, R.O. Heat Exchanger Design Guide: A Practical Guide for Planning, Selecting and Designing of Shell and Tube Exchangers; Butterworth-Heinemann: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Kakaç, S.; Liu, H.; Pramuanjaroenkij, A. Heat Exchangers: Selection, Rating, and Thermal Design, 4th ed.; CRC Press: Boca Raton, FL, USA, 2020; pp. 4–6. [Google Scholar]
- Gulyani, B.B. Estimating Number of Shells in Shell and Tube Heat Exchangers: A New Approach Based on Temperature Cross. ASME. J. Heat Trans. 2000, 122, 566–571. [Google Scholar] [CrossRef]
- Bell, K.J. Heat Exchanger Design for the Process Industries. J. Heat Transfer. 2004, 126, 877–885. [Google Scholar] [CrossRef]
- Master, B.I.; Chunangad, K.S.; Boxma, A.J.; Kral, D.; Stehlík, P. Most Frequently Used Heat Exchangers from Pioneering Research to Worldwide Applications. Heat Trans. Eng. 2006, 27, 4–11. [Google Scholar] [CrossRef]
- Standards of the Tubular Exchanger Manufacturers Association, 10th ed.; Tubular Exchanger Manufacturers Association, Inc.: New York, NY, USA, 2019; pp. 5.7-11–5.7-12, 10–31.
- Yokell, S. Heat exchanger tube-tubesheet connection. Chem. Eng. 1982, 75, 78–94. [Google Scholar]
- Jawad, M.H.; Clark, E.J.; Schuessler, R.E. Evaluation of tube-to-tubesheet junctions. Trans. ASME J. Press. Vessel Technol. 1987, 109, 19–26. [Google Scholar] [CrossRef]
- Yokell, S. Heat Exchanger Tube-to Tubesheet Connections. The Chemical Engineering Guide to Heat Tranfer: Plant Principles, 1st ed.; McNaughton, K.J., Ed.; Hemisphere: New York, NY, USA, 1986; pp. 76–92. Volume 1. [Google Scholar]
- Yokell, S. Expanded, and Welded-and-Expanded Tube-to-Tubesheet Joints. J. Press. Vessel. Technol. 1992, 114, 157–165. [Google Scholar] [CrossRef] [Green Version]
- Yokell, S. Heat Exchangers: Tube-to-Tubesheet Joint Tightness. Chem. Eng. Heat Trans. 2007, 114, 46–51. [Google Scholar]
- Ali, M.; Ul-Hamid, A.; Alhems, L.M.; Saeed, A. Review of common failures in heat exchangers. Part I: Mechanical and elevated temperature failures. Eng. Fail. Anal. 2020, 109, 104396. [Google Scholar] [CrossRef]
- Xu, S.; Wang, C.; Wang, W. Failure analysis of stress corrosion cracking in heat exchanger tubes during start-up operation. Eng. Fail. Anal. 2015, 51, 1–8. [Google Scholar] [CrossRef]
- Thekkuden, D.T.; Mourad, A.-H.I.; Bouzid, A.-H. Failures and leak inspection techniques of tube-to-tubesheet joints: A review. Eng. Fail. Anal. 2021, 130, 105798. [Google Scholar] [CrossRef]
- Wang, H.; Sang, Z.; Widera, G.E.O. Connection strength and tightness of hydraulically expanded tube-to-tubesheet joints. J. Mater. Process. Technol. 2007, 194, 93–99. [Google Scholar] [CrossRef]
- Sang, Z.F.; Zhu, Y.Z.; Widera, G.E.O. Reliability factors and tightness of tube-to-tubesheet joints. Trans. ASME J. Pressure Vessel Technol. 1996, 118, 137–141. [Google Scholar] [CrossRef]
- Scott, D.A.; Wolgemuth, G.A.; Aikin, J.A. Hydraulically expanded tube-to-tubesheet joints. Trans. ASME J. Pressure Vessel Technol. 1984, 106, 104–109. [Google Scholar] [CrossRef]
- Weinstock, S.; Reinis, K.; Soler, A. Tube-to-tube joint interfacing pressure: Analysis and experiments. Trans. ASME J. Pressure Vessel Technol. 1987, 109, 193–199. [Google Scholar] [CrossRef]
- Goodier, J.N.; Schoessow, G.J. The holding power and hydraulic tightness of expanded tube joints: Analysis of the stress and deformation. Trans. ASME J. Pressure Vessel Technol. 1943, 65, 489–496. [Google Scholar] [CrossRef]
- Allam, M.; Chaaban, A.; Bazergui, A. Estimation of residual stresses in hydraulically expanded tube-to-tubesheet joints. Trans. ASME J. Pressure Vessel Technol. 1998, 120, 129–137. [Google Scholar] [CrossRef]
- Kohlpaintner, W.R. Calculation of hydraulically expanded tube-to-tubesheet joints. Trans. ASME J. Pressure Vessel Technol. 1995, 117, 24–30. [Google Scholar] [CrossRef]
- Ma, H.; Yu, H.J.; Qian, C.F.; Liu, Z.S.; Zhou, J.X. Experimental Study of Hydraulically Expanded Tube-to-Tubesheet Joints for Shell-and-Tube Heat Exchangers. Procedia Eng. 2015, 130, 263–274. [Google Scholar] [CrossRef] [Green Version]
- Shuaib, A.N. Setting initial clearance limits for sound roller expanded tube-tubesheet joints in shell and tube heat exchanger maintenance. J. Qual. Maint. Eng. 2006, 12, 89–99. [Google Scholar] [CrossRef]
- Shuaib, A.N.; Merah, N.; Khraisheh, M.K.; Allam, I.M.; Al-Anizi, S.S. Experimental investigation of heat exchanger tubesheet hole enlargement. ASME J. Pressure Vessel Technol. 2003, 125, 19–25. [Google Scholar] [CrossRef]
- Alam, M.; Bazergui, A. Axial strength of tube-to-tubesheet joints: Finite element and experimental evaluations. ASME J. Pressure Vessel Technol. 2002, 124, 22–31. [Google Scholar] [CrossRef]
- Thekkuden, D.T.; Mourad, A.-H.I.; Bouzid, A.-H.; Sherif, M.M. Investigation of expansion percentages and groove inclusions on the performance of welded, expanded, welded-expanded tube-to-tubesheet joints. J. Mater. Res. Technol. 2023, 22, 2078–2092. [Google Scholar] [CrossRef]
- Wang, H.F.; Sang, Z.F. Effect of geometry of grooves on connection strength of hydraulically expanded tube-to-tubesheet joints. ASME J. Pressure Vessel Technol. 2005, 127, 430–435. [Google Scholar] [CrossRef]
- Wang, H.F.; Sang, Z.F.; Widera, G.E.O. Contact stress in the expanded zone of expanded-welded tube-to-tubesheet joints. ASME J. Pressure Vessel Technol. 2011, 133, 061209. [Google Scholar] [CrossRef]
- Thekkuden, D.T.; Mourad, A.-H.I.; Ramachandran, T.; Bouzid, A.-H.; Kumar, R.; Alzamly, A. Combined effect of tungsten inert gas welding and roller expansion processes on mechanical and metallurgical characteristics of heat exchanger tube-to-tubesheet joints. J. Mater. Res. Technol. 2022, 21, 4724–4744. [Google Scholar] [CrossRef]
- Womack, J.P.; Jones, D.T. Lean Thinking: Banish Waste and Create Wealth in Your Corporation, 2nd ed.; Revised and updated; Free Press: New York, NY, USA, 2003. [Google Scholar]
- Dhingra, R.; Kress, R.; Upreti, G. Does lean mean green? J. Clean. Prod. 2014, 85, 1–7. [Google Scholar] [CrossRef]
- Johansson, G.; Sundin, E. Lean and green product development: Two sides of the same coin? J. Clean. Prod. 2014, 85, 104–121. [Google Scholar] [CrossRef] [Green Version]
- Garza-Reyes, J.A. Lean and green—A systematic review of the state of the art literature. J. Clean. Prod. 2015, 102, 18–29. [Google Scholar] [CrossRef] [Green Version]
- Fercoq, A.; Lamouri, S.; Carbone, V. Lean/Green integration focused on waste reduction techniques. J. Clean. Prod. 2016, 137, 567–578. [Google Scholar] [CrossRef]
- Ward, A.C.; Sobek II, D.K. Lean Product and Process Development, 2nd ed.; Lean Enterprise Institute Inc.: Boston, MA, USA, 2014. [Google Scholar]
- George, M.; Works, J.; Watson-Hemphill, K. Fast Innovation: Achieving Superior Differentiation, Speed to Market, and Increased Profitability; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Pyzdek, T.; Keller, P. The Six Sigma Handbook; McGraw-Hill: New York, NY, USA, 2018. [Google Scholar]
- George, M.; Rowlands, D.; Price, M.; Maxey, J. The Lean Six Sigma Pocket Toolbook; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- George, M.; Blackwell, D.; Rajan, D. Lean Six Sigma in the Age of Artificial Intelligence: Harnessing the Power of the Fourth Industrial Revolution; McGraw-Hill: New York, NY, USA, 2019. [Google Scholar]
- Tanco, M.; Viles, E.; Ilzarbe, L.; Alvarez, M.J. Implementation of Design of Experiments projects in industry. Qual. Reliab. Eng. Int. 2009, 25, 478–505. [Google Scholar] [CrossRef]
- Ilzarbe, L.; Alvarez, M.J.; Viles, E.; Tanco, M. Practical applications of design of experiments in the field of engineering: A bibliographical review. Qual. Reliab. Eng. Int. 2008, 24, 417–428. [Google Scholar] [CrossRef]
- Taguchi, G.; Chowdhury, S.; Wu, Y. Taguchi’s Quality Engineering Handbook, 1st ed.; Wiley-Interscience: Hoboken, NJ, USA, 2004. [Google Scholar]
- Taguchi, G.; Chowdhury, S.; Taguchi, S. Robust Engineering: Learn. How to Boost Quality While Reducing Costs and Time to Market; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Breiman, L. Statistical modeling: The two cultures. Stat. Sci. 2001, 16, 199–231. [Google Scholar] [CrossRef]
- Fisher, R.A. The Design of Experiments; Macmillan: New York, NY, USA, 1971. [Google Scholar]
- Fisher, R.A. Statistical Methods, Experimental Design, and Scientific Inference; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Box, G.E.P. Signal-to-noise ratios, performance criteria and transformation. Technometrics 1998, 30, 1–17. [Google Scholar] [CrossRef]
- Maghsoodloo, S.; Ozdemir, G.; Jordan, V.; Huang, C.-H. Strengths and limitations of Taguchi’s contributions to quality, manufacturing, and process engineering. J. Manuf. Syst. 2004, 23, 73–126. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Thomas, C.; Wilson, L.L.C. Basic Guidelines of Tube Expanding. Available online: https://www.tcwilson.com/t/tube-rolling-basic-guidelines (accessed on 15 January 2021).
- Elliott Tool Technologies. TM-6 02-10-2004. Basic Principles of Tube Expanding. Available online: https://www.elliott-tool.com/media/tools/Basic-Principles-of-Tube-Expanding.pdf (accessed on 15 January 2021).
- R Core Team. R: A Language and Environment for Statistical Computing; ver. 4.2.2.; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 31 October 2022).
- Boulougouras, P. Optimization of a Tube-to-Tubesheet Expanded Joint in a Shell-and-Tube Heat Exchanger Using Taguchi Methods. Master’s Thesis, Kingston University, London, UK, 2021. [Google Scholar]










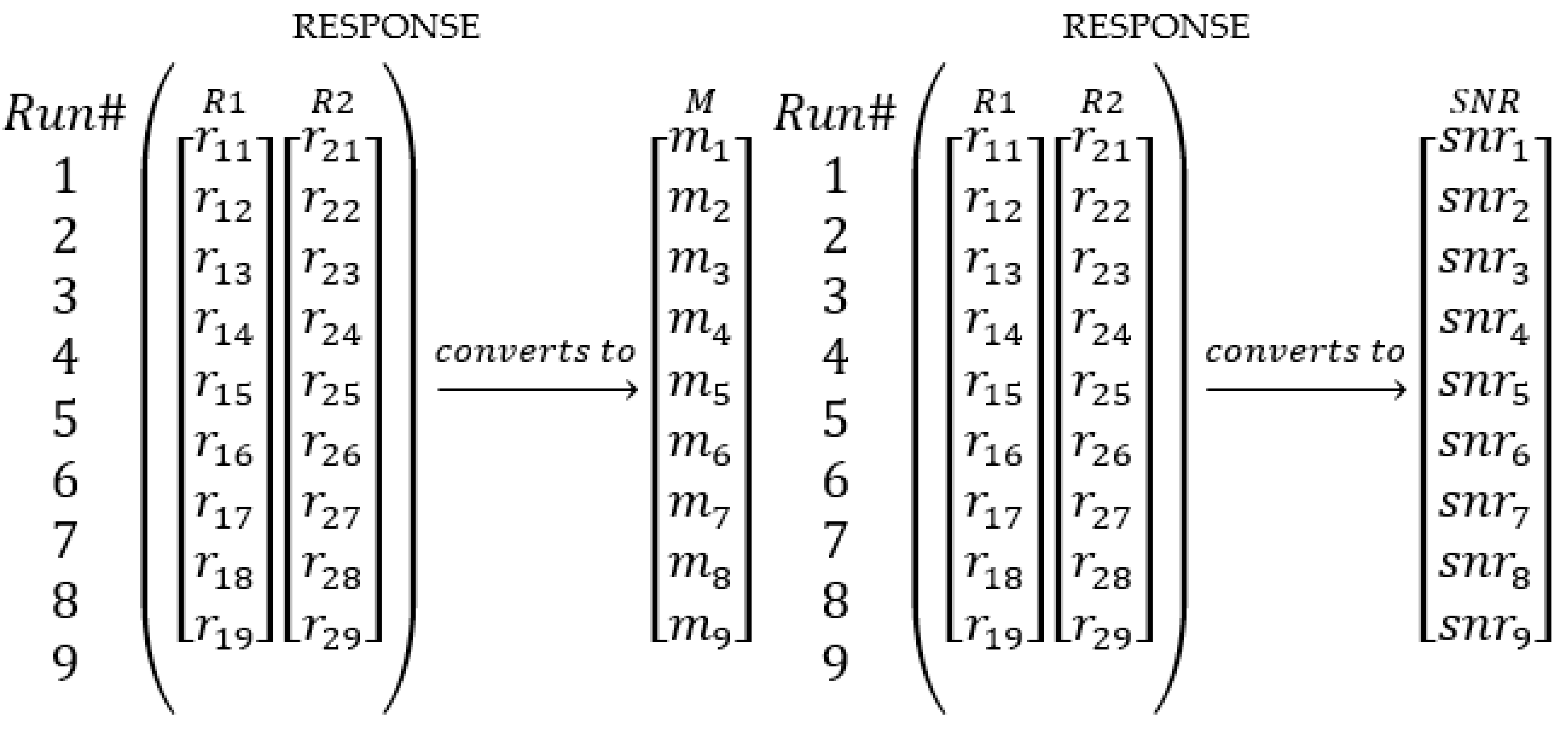







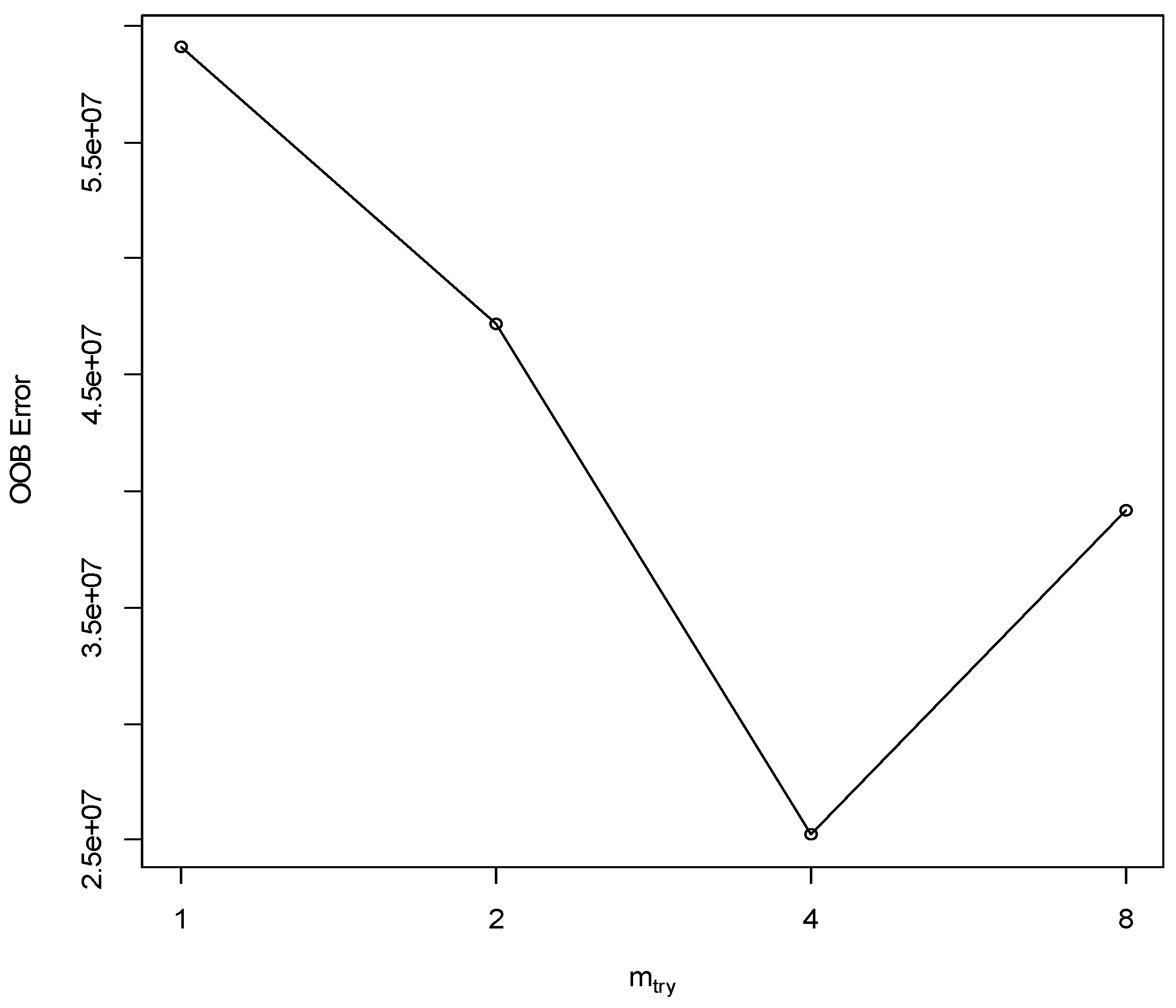
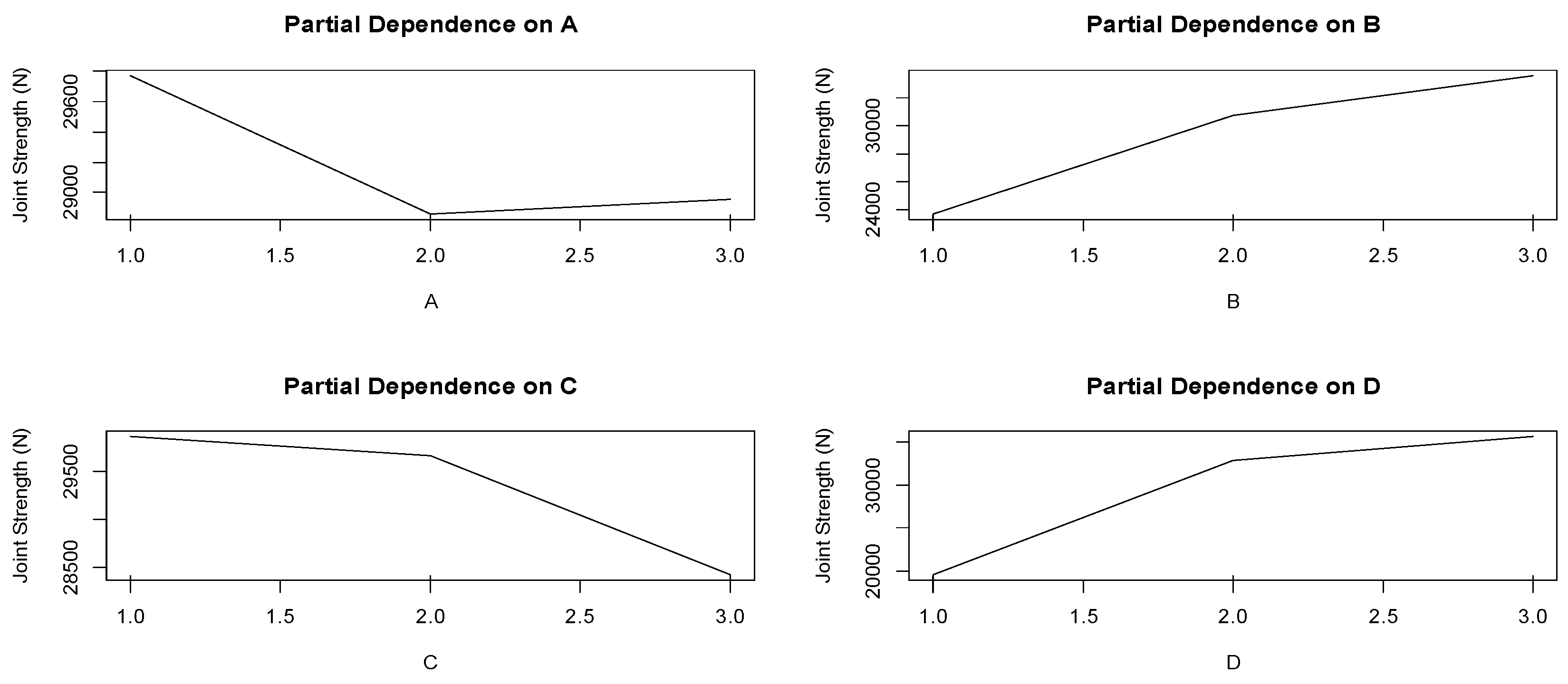
| Controlling Factor (Units) | Level 1 | Level 2 | Level 3 | |
|---|---|---|---|---|
| 1 | Clearance (mm) | 0.10 | 0.25 | 0.40 |
| 2 | Number of Grooves | One | Two | Three |
| 3 | Groove Depth (mm) | 0.20 | 0.40 | 0.60 |
| 4 | Tube Wall Thickness Reduction (%) | 4 | 8 | 12 |
| Run | Clearance | Number of Grooves | Groove Depth | Tube Wall Thickness Reduction |
|---|---|---|---|---|
| 1 | 0.10 ± 0.02 | One | 0.20 ± 0.02 | 4 |
| 2 | 0.10 ± 0.02 | Two | 0.40 ± 0.02 | 8 |
| 3 | 0.10 ± 0.02 | Three | 0.60 ± 0.02 | 12 |
| 4 | 0.25 ± 0.02 | One | 0.40 ± 0.02 | 12 |
| 5 | 0.25 ± 0.02 | Two | 0.60 ± 0.02 | 4 |
| 6 | 0.25 ± 0.02 | Three | 0.20 ± 0.02 | 8 |
| 7 | 0.40 ± 0.02 | One | 0.60 ± 0.02 | 8 |
| 8 | 0.40 ± 0.02 | Two | 0.20 ± 0.02 | 12 |
| 9 | 0.40 ± 0.02 | Three | 0.40 ± 0.02 | 4 |
| Type P265GH (1.0425)/EN 10028-2 | ||||||
| Chemical Composition % | ||||||
| C | Mn | Si | P | S | Cu | Ni |
| Max 0.2 | 0.8–1.4 | Max 0.4 | Max 0.025 | Max 0.01 | Max 0.3 | Max 0.3 |
| Cr | Mo | Al | V | Nb | Ti | N |
| Max 0.3 | Max 0.08 | Min 0.02 | Max 0.02 | Max 0.03 | Max 0.03 | Max 0.012 |
| Mechanical Properties | ||||||
| Yield strength (ReH) [MPa] | Min 255 | |||||
| Tensile strength (Rm) [MPa] | 410–530 | |||||
| Elongation (A%) | Min 22 | |||||
| Type P215NL (1.0451)/EN 10216-4 | ||||||
| Chemical Composition % | ||||||
| C | Mn | Si | P | S | Cu | Ni |
| 0.09 | 0.48 | 0.18 | 0.011 | 0.002 | 0.01 | 0.02 |
| Cr | Mo | Al | V | Nb | Ti | |
| 0.03 | 0.01 | 0.028 | 0.001 | 0.001 | 0.003 | |
| Mechanical Properties | ||||||
| Yield strength (ReH) [MPa] | Min 225 | |||||
| Tensile strength (Rm) [MPa] | Min 360 | |||||
| Elongation (A%) | Min 25 | |||||
| Tube Wall Thickness Reduction (%) | Torque (Nm) |
|---|---|
| 4 | 8 |
| 8 | 12 |
| 12 | 15 |
| Run# | Joint Strength (N) Trial #1 | Joint Strength (N) Trial #2 | Joint Strength Mean (N) | SNR-Joint Strength (dB) |
|---|---|---|---|---|
| 1 | 17,880.00 | 16,597.50 | 17,238.75 | 84.71 |
| 2 | 37,552.50 | 38,400.00 | 37,976.25 | 91.60 |
| 3 | 45,371.25 | 44,913.75 | 45,142.50 | 93.09 |
| 4 | 31,263.75 | 29,811.25 | 30,537.50 | 89.70 |
| 5 | 11,935.00 | 13,500.00 | 12,717.50 | 82.04 |
| 6 | 39,768.75 | 39,330.00 | 39,549.38 | 91.94 |
| 7 | 17,523.75 | 18,288.75 | 17,906.25 | 85.05 |
| 8 | 38,662.50 | 37,706.25 | 38,184.38 | 91.64 |
| 9 | 24,318.75 | 26,525.00 | 25,421.88 | 88.08 |
| Level | Clearance | Number of Grooves | Groove Depth | Tube Wall Thickness Reduction |
|---|---|---|---|---|
| 1 | 33,452.50 | 21,894.17 | 31,657.50 | 18,459.37 |
| 2 | 27,601.46 | 29,626.04 | 31,311.87 | 31,810.62 |
| 3 | 27,170.83 | 36,704.58 | 25,255.42 | 37,954.79 |
| Difference | 6281.67 | 14,810.42 | 6402.08 | 19,495.42 |
| Rank | 4 | 2 | 3 | 1 |
| Level | Clearance | Number of Grooves | Groove Depth | Tube Wall Thickness Reduction |
|---|---|---|---|---|
| 1 | 89.80 | 86.49 | 89.43 | 84.94 |
| 2 | 87.89 | 88.42 | 89.79 | 89.53 |
| 3 | 88.26 | 91.04 | 86.73 | 91.47 |
| Delta | 1.91 | 4.55 | 3.06 | 6.53 |
| Rank | 4 | 2 | 3 | 1 |
| Factor | DF | adj SS | adj MS | F-Value | p-Value | Contribution (%) | Rank |
|---|---|---|---|---|---|---|---|
| Clearance | 2 | 73,879,463 | 36,939,731 | * | * | 6.86 | 4 |
| Number of Grooves | 2 | 329,236,085 | 164,618,042 | * | * | 30.57 | 2 |
| Groove Depth | 2 | 77,786,815 | 38,893,408 | * | * | 7.22 | 3 |
| Tube Wall Thk. Reduction | 2 | 596,077,932 | 298,038,966 | * | * | 55.35 | 1 |
| Error | 0 | * | * | * | |||
| Total | 8 | 1,076,980,294 | 100.00 | ||||
| Model Summary | |||||||
| S R-sq R-sq (adj) R-sq (pred) | |||||||
| * 100.00% * * | |||||||
| Factor | DF | adj SS | adj MS | F-Value | p-Value | Contribution (%) | Rank |
|---|---|---|---|---|---|---|---|
| Clearance | 2 | 6.146 | 3.073 | * | * | 5.05 | 4 |
| Number of Grooves | 2 | 31.321 | 15.661 | * | * | 25.74 | 2 |
| Groove Depth | 2 | 16.777 | 8.389 | * | * | 13.79 | 3 |
| Tube Wall Thk. Reduction | 2 | 67.423 | 33.712 | * | * | 55.42 | 1 |
| Error | 0 | * | * | * | |||
| Total | 8 | 121.668 | 100.00 | ||||
| Model Summary | |||||||
| S R-sq R-sq (adj) R-sq (pred) | |||||||
| * 100.00% * * | |||||||
| Source | DF | adj SS | adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Regression | 7 | 2,153,533,744 | 307,647,678 | 423.04 | 0.000 |
| A | 1 | 118,378,008 | 118,378,008 | 162.78 | 0.000 |
| B | 1 | 658,045,326 | 658,045,326 | 904.86 | 0.000 |
| C | 1 | 122,960,013 | 122,960,013 | 169.08 | 0.000 |
| D | 1 | 1,140,213,813 | 1,140,213,813 | 1567.87 | 0.000 |
| A∗A | 1 | 29,380,917 | 29,380,917 | 40.40 | 0.000 |
| C∗C | 1 | 32,613,617 | 32,613,617 | 44.85 | 0.000 |
| D∗D | 1 | 51,942,050 | 51,942,050 | 71.42 | 0.000 |
| Error | 10 | 7,272,359 | 727,236 | ||
| Lack-of-Fit | 1 | 426,844 | 426,844 | 0.56 | 0.473 |
| Pure Error | 9 | 6,845,515 | 760,613 | ||
| Total | 17 | 2,160,806,104 | |||
| Model | Summary | ||||
| S | R2 | R2 (adj) | R2 (pred) | ||
| 852.78 | 99.66% | 99.43% | 98.89% |
| Term | COEF | SE COEF | T-Value | p-Value | VIF |
|---|---|---|---|---|---|
| Constant | 31,907 | 532 | 60.00 | 0.000 | |
| A | −3141 | 246 | −12.76 | 0.000 | 1.00 |
| B | 7405 | 246 | 30.08 | 0.000 | 1.00 |
| C | −3201 | 246 | −13.00 | 0.000 | 1.00 |
| D | 9748 | 246 | 39.60 | 0.000 | 1.00 |
| A∗A | 2710 | 426 | 6.36 | 0.000 | 1.00 |
| C∗C | −2855 | 426 | −6.70 | 0.000 | 1.00 |
| D∗D | −3604 | 426 | −8.45 | 0.000 | 1.00 |
| Regression | Equation: | ||||
| Joint Strength | = | 31907 − 3141 A + 7405 B − 3201 C + 9748 D + 2710 A2 − 2855 C2 − 3604 D2 | |||
| Total Variables | R2 | R2 (adj) | PRESS | R2 (Pred) | Mallows’s CP | S | A | C |
|---|---|---|---|---|---|---|---|---|
| 3 | 88.9 | 86.5 | 323,492,722.0 | 85.0 | 15.7 | 4136.8 | X | |
| 3 | 88.7 | 86.3 | 374,906,004.8 | 82.6 | 16.2 | 4176.2 | X | |
| 4 | 94.4 | 92.7 | 199,192,722.4 | 90.8 | 5.0 | 3053.5 | X | X |
| Prediction Method | Predicted Maximum Joint Strength |
|---|---|
| Taguchi Method | Mean = 51,199.00 N (s = 729 N) SNR = 96.1 dB |
| Stepwise Regression | 51,307 N |
| Run# | Max. Joint Strength (N) | Max. Joint Strength Mean (N) |
|---|---|---|
| 1 | 44,013.75 | = 43,861.75 ( = 424.45) 95% C.I. (43,334.73, 44,388.77) Coefficient of Variation = 0.0098 |
| 2 | 43,218.75 | |
| 3 | 44,392.50 | |
| 4 | 43,813.75 | |
| 5 | 43,870.00 |
| N | Mean | Std. Deviation | Std. Error Mean | 95% Confidence Interval | ||
|---|---|---|---|---|---|---|
| Lower | Upper | |||||
| MSR | 10 | 17,843,680 | 1,115,982 | 352,904 | 17,045,354 | 18,642,006 |
| VE | 10 | 85.13 | 0.93 | 0.29 | 84.47 | 85.80 |
| MSE A | 10 | 8.03 | 0.75 | 0.24 | 7.50 | 8.57 |
| MSE B | 10 | 25.06 | 0.61 | 0.19 | 24.62 | 25.50 |
| MSE C | 10 | 3.74 | 0.99 | 0.31 | 3.03 | 4.45 |
| MSE D | 10 | 33.21 | 0.95 | 0.30 | 32.53 | 33.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boulougouras, P.; Besseris, G. Lean-and-Green Strength Performance Optimization of a Tube-to-Tubesheet Joint for a Shell-and-Tube Heat Exchanger Using Taguchi Methods and Random Forests. Processes 2023, 11, 1211. https://doi.org/10.3390/pr11041211
Boulougouras P, Besseris G. Lean-and-Green Strength Performance Optimization of a Tube-to-Tubesheet Joint for a Shell-and-Tube Heat Exchanger Using Taguchi Methods and Random Forests. Processes. 2023; 11(4):1211. https://doi.org/10.3390/pr11041211
Chicago/Turabian StyleBoulougouras, Panagiotis, and George Besseris. 2023. "Lean-and-Green Strength Performance Optimization of a Tube-to-Tubesheet Joint for a Shell-and-Tube Heat Exchanger Using Taguchi Methods and Random Forests" Processes 11, no. 4: 1211. https://doi.org/10.3390/pr11041211





