The Optimal Branch Width Convergence Ratio to Maximize the Transport Efficiency of the Combined Electroosmotic and Pressure-Driven Flow within a Fractal Tree-like Convergent Microchannel
Abstract
:1. Introduction
2. Description of the FTCMC
3. Numerical Method
3.1. Numerical Setup
- (1)
- The combined EOF and PDF is a three-dimensional incompressible steady and Newtonian fluid flow.
- (2)
- The channel widths and height of the microchannel are supposed to be much larger than the Debye length to avoid the overlap of EDL.
- (3)
- Zeta potential at the microchannel wall is uniform and low enough to enable Debye–Hückel linearization.
- (4)
- No slip condition is applied on the solid–liquid interfaces.
- (1)
- Inlet: The voltage VE is set at the channel inlet, as shown in Equation (9); the pressure Pin is maintained at the inlet, as shown in Equation (10); and the inlet ionic concentration is set to 1 mM, as shown in Equation (11),
- (2)
- Outlet: The outlet potential is set to be zero, as shown in Equation (12); and the outlet pressure is 0 Pa, as shown in Equation (13),
- (3)
- Solid–liquid wall: The Helmholtz–Smoluchowski slip velocity was employed at the solid–liquid wall, and there was no electric potential change given in Equation (14) and no mass flux across the wall given in Equation (15):
3.2. Mesh Independence Test and Data Validation
4. Results and Discussions
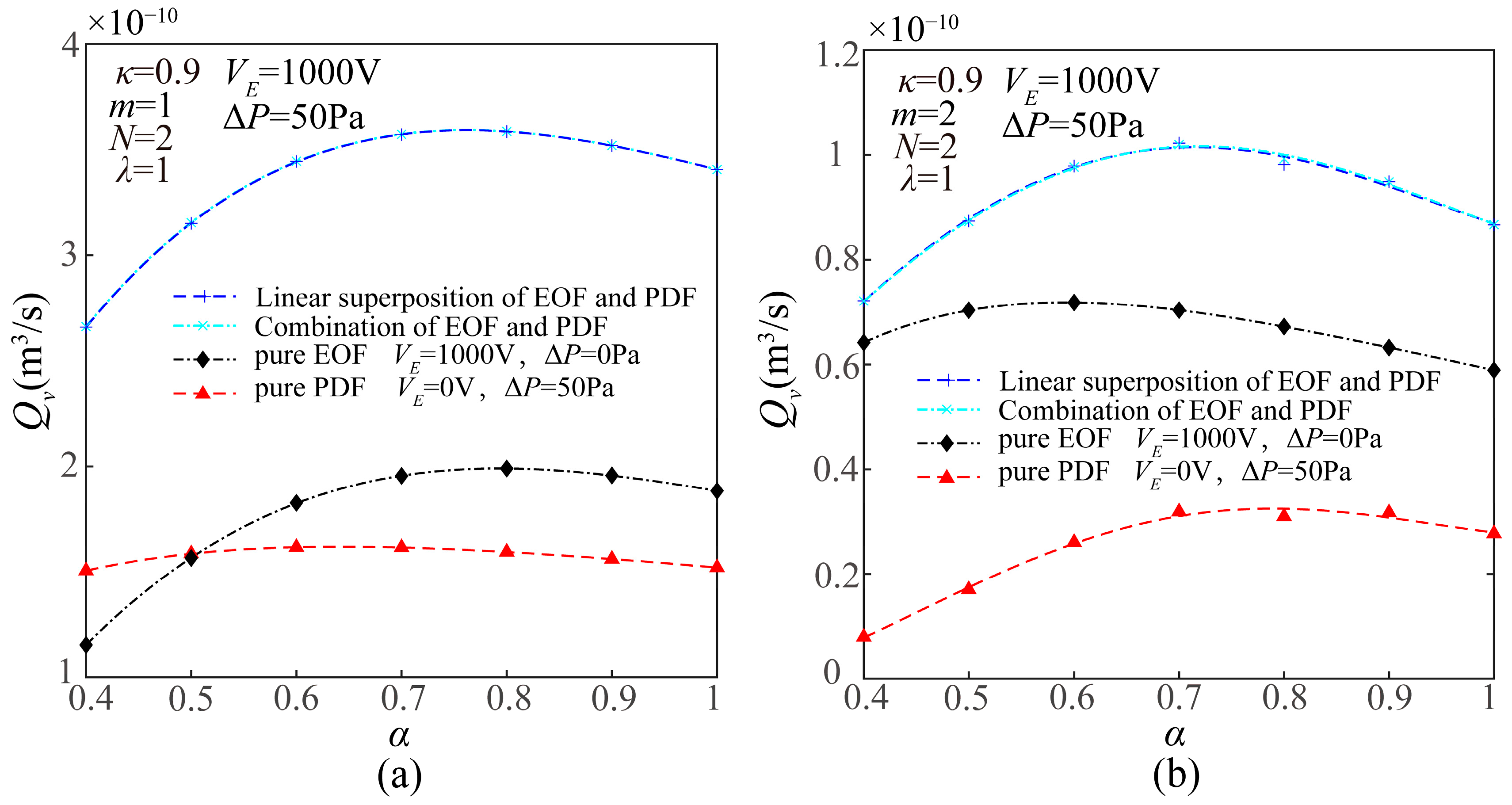
4.1. Impact of Branch Convergence Ratio on the Flow rate within FTCMC
4.2. Impact of Ratio of Voltage Difference and Pressure Difference on αopt
4.3. Impacts of Length Ratio, Branching Number, and Branching Level on αopt
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| c | ions concentration |
| cinlet | inlet concentration |
| Dc | diffusion coefficient |
| e | elementary charge |
| E | applied electric field strength |
| H | channel height |
| kb | Boltzmann constant |
| li | each channel length |
| m | branching level |
| n0 | liquid bulk ionic concentration |
| N | branching number |
| p | fluid pressure |
| pinlet | inlet pressure |
| poutlet | outlet pressure |
| Qv | flow rate |
| Re | Reynolds number |
| Si | each channel bottom area |
| T | absolute temperature |
| v | velocity vector |
| Vi | each channel volume |
| V | total channel volume |
| VE | voltage |
| wi | each channel width |
| z | chemical valence of ions |
| Greek letters | |
| α | branch convergence |
| αopt | optimal branch convergence |
| β | branch angle |
| Δp | pressure drop |
| ε0 | vacuum permittivity |
| εr | relative permittivity of liquid |
| ζ | zeta potential |
| κ | level convergence |
| λ | length ratio |
| μ | fluid dynamic viscosity |
| ρ | fluid density |
| ρe | net charge density |
| φ | applied electric potential |
| φinlet | inlet potential |
| φoutlet | outlet potential |
| Φ | electrical potential |
| ψ | EDL electric potential |
| Abbreviations | |
| EDL | electrical double layer |
| EOF | electroosmotic flow |
| pressure driven flow | |
| FTCMC | fractal tree-like convergent microchannel |
References
- Li, D.Q. Encyclopedia of Microfluidics and Nanofluidics; Springer: New York, NY, USA, 2008. [Google Scholar]
- Lin, B. Microfluidics: Technologies and Applications; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Kandlikar, S.G.; Garimella, S.; Li, D.Q.; Colin, S.; King, M.R. Heat Transfer and Fluid Flow in Minichannels and Microchannels; Elsevier: Oxford, UK, 2006. [Google Scholar]
- Beebe, D.J.; Mensing, G.A.; Walker, G.M. Physics and applications of microfluidics in biology. Annu. Rev. Biomed. Eng. 2002, 4, 261–286. [Google Scholar] [CrossRef] [PubMed]
- Bojang, A.A.; Wu, H.S. Design, fundamental principles of fabrication and applications of microreactors. Processes 2020, 8, 891. [Google Scholar] [CrossRef]
- Yao, X.; Zhang, Y.; Du, L.; Liu, J.; Yao, J. Review of the applications of microreactors. Renew. Sustain. Energy Rev. 2015, 47, 519–539. [Google Scholar] [CrossRef]
- Shourabi, A.Y.; Kashaninejad, N.; Saidi, M.S. An integrated microfluidic concentration gradient generator for mechanical stimulation and drug delivery. J. Sci. Adv. Mater. Devices 2021, 6, 280–290. [Google Scholar] [CrossRef]
- Bejan, A.; Zane, J.P. Design in Nature. Mechical Eng. 2012, 134, 42–47. [Google Scholar] [CrossRef]
- Xu, P.; Sasmito, A.P.; Yu, B.; Mujumdar, A.S. Transport phenomena and properties in tree-like networks. Appl. Mech. Rev. 2016, 68, 040802. [Google Scholar] [CrossRef]
- Samal, S.K.; Qadeer, M.; Saha, S.K. thermo-hydraulic performance evaluation of radial tree-branching microchannel heat sinks for electronic cooling applications. Int. J. Therm. Sci. 2024, 197, 108800. [Google Scholar] [CrossRef]
- Chen, Y.; Cheng, P. Heat transfer and pressure drop in fractal tree-like microchannel nets. Int. J. Heat Mass. Transf. 2002, 45, 2643–2648. [Google Scholar] [CrossRef]
- Ji, X.; Yang, X.; Zhang, Y.; Zhang, Y.; Wei, J. Experimental study of ultralow flow resistance fractal microchannel heat sinks for electronics cooling. Int. J. Therm. Sci. 2022, 179, 107723. [Google Scholar] [CrossRef]
- Ma, C.; Sun, Y.; Wu, Y.; Zhang, Q.; Wang, Y.; Ding, G. A bio-inspired fractal microchannel heat sink with secondary modified structure and sub-total-sub fluid transmission mode for high heat flux and energy-saving heat dissipation. Int. J. Heat Mass Transf. 2023, 202, 123717. [Google Scholar] [CrossRef]
- Lovchik, R.D.; Tonna, N.; Bianco, F.; Matteoli, M.; Delamarche, E. A microfluidic device for depositing and addressing two cell populations with intercellular population communication capability. Biomed. Microdevices 2010, 12, 275–282. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Koo, L.Y.; Wang, W.M.; Lauffenburger, D.A.; Griffifith, L.G.; Jensen, K.F. Microfluidic shear devices for quantitative analysis of cell adhesion. Anal. Chem. 2004, 76, 5257–5264. [Google Scholar] [CrossRef] [PubMed]
- Senn, S.M.; Poulikakos, D. Laminar mixing, heat transfer and pressure drop in tree-like microchannel nets and their application for thermal management in polymer electrolyte fuel cells. J. Power Sources 2004, 130, 178–191. [Google Scholar] [CrossRef]
- Kjelstrup, S.; Coppens, M.O.; Pharoah, J.G.; Pfeifer, P. Nature-inspired energy-and material-efficient design of a polymer electrolyte membrane fuel cell. Energy Fuels 2010, 24, 5097–5108. [Google Scholar] [CrossRef]
- Chakraborty, S. Microfluidics and Microfabrication; Springer: Boston, MA, USA, 2010. [Google Scholar]
- Karniadakis, G.E.; Beskok, A.; Gad-el-Hak, M. Micro flows: Fundamentals and Simulation. Appl. Mechenics Rev. 2002, 55, B76. [Google Scholar] [CrossRef]
- Jing, D.; Bhushan, B. The coupling of surface charge and boundary slip at the solid–liquid interface and their combined effect on fluid drag: A review. J. Colloid Interface Sci. 2015, 454, 152–179. [Google Scholar] [CrossRef] [PubMed]
- Li, D. Electrokinetics in Microflfluidics; Academic Press: Oxford, UK, 2004. [Google Scholar]
- Chen, Q.; Shyu, S.; Li, W. An overlapped electrical double layer model for aqueous electrolyte lubrication with asymmetric surface electric potentials. Tribol. Int. 2020, 147, 106283. [Google Scholar] [CrossRef]
- Sasaki, N.; Kitamori, T.; Kim, H.B. AC electroosmotic micromixer for chemical processing in a microchannel. Lab A Chip 2006, 6, 550–554. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Cheng, C.; Wang, S.; Liu, S. Electroosmotic pumps and their applications in microfluidic systems. Microfluid. Nanofluidics 2009, 6, 145–162. [Google Scholar] [CrossRef]
- Dutta, P.; Horiuchi, K.; Yin, H.-M. Thermal Characteristics of Mixed Electroosmotic and Pressure-Driven Microflows. Comput. Math. Appl. 2006, 52, 651–670. [Google Scholar] [CrossRef]
- Babaie, A.; Sadeghi, A.; Saidi, M.H. Combined electroosmotically and pressure driven flow of power-law fluids in a slit microchannel. J. Non-Newton. Fluid Mech. 2011, 166, 792–798. [Google Scholar]
- Ebrahimi, S.; Hasanzadeh-Barforoushi, A.; Nejat, A.; Kowsary, F. Numerical study of mixing and heat transfer in mixed electroosmotic/pressure driven flow through T-shaped microchannels. Int. J. Heat Mass Transf. 2014, 75, 565–580. [Google Scholar] [CrossRef]
- Mondal, M.; Misra, R.P.; De, S. Combined electroosmotic and pressure driven flow in a microchannel at high zeta potential and overlapping electrical double layer. Int. J. Therm. Sci. 2014, 86, 48–59. [Google Scholar] [CrossRef]
- Deng, S.; Xiao, T.; Liang, C. Analytical study of unsteady two-layer combined electroosmotic and pressure-driven flow through a cylindrical microchannel with slip-dependent zeta potential. Chem. Eng. Sci. 2024, 283, 119327. [Google Scholar] [CrossRef]
- Hegde, A.S.; Harikrishnan, A.R. Slip hydrodynamics of combined electroosmotic and pressure driven flows of power law fluids through narrow confinements. Eur. J. Mech. B/Fluids 2021, 89, 525–550. [Google Scholar]
- Feng, Q.; Chen, X.; Wang, X.; Yu, X.; Zeng, X.; Ma, Y.; Wang, Q. Numerical simulation of a three dimensional electroosmotic micromixer with a flexible and controllable Rubik’s cube module. Int. Commun. Heat Mass Transf. 2021, 127, 105482. [Google Scholar] [CrossRef]
- An, S.; Tian, K.; Ding, Z.; Jian, Y. Electroosmotic and pressure-driven slip flow of fractional viscoelastic fluids in microchannels. Appl. Math. Comput. 2022, 425, 127073. [Google Scholar] [CrossRef]
- Alshammari, F.S.; Akyildiz, F.T. Pseudo spectral solution of extended Graetz problem for combined pressure-driven and electroosmotic flow in a triangular micro-duct. Comput. Math. Appl. 2020, 80, 990–1008. [Google Scholar] [CrossRef]
- Barrot, C.; Colin, S.P. Electroosmotic flow in tree-shaped microchannel networks. In Proceedings of the 6th International Conference on Nanochannels, Microchannels, and Minichannels, Darmstadt, Germany, 23–25 June 2008; Volume 48345, pp. 419–426. [Google Scholar]
- Barrot, C.; Colin, S.P. Design of tree-shaped microchannel networks submitted to simultaneous pressure driven and electro-osmotic flows. In Proceedings of the 10th International Conference on Nanochannels, Microchannels, and Minichannels, Rio Grande, PR, USA, 8–12 July 2012; Volume 44793, pp. 113–121. [Google Scholar]
- Jing, D.; Yi, S. Electroosmotic flow in tree-like branching microchannel network. Fractals 2019, 27, 1950095. [Google Scholar] [CrossRef]
- Liu, F.; Jing, D. Combined electroosmotic and pressure driven flow in tree-like microchannel network. Fractals 2021, 29, 2150110. [Google Scholar] [CrossRef]
- Zhang, J.; Shu, S.; Guan, X.; Yang, N. Lattice Boltzmann simulation of drop splitting in a fractal tree-like microchannel. Chem. Eng. Sci. 2022, 252, 117277. [Google Scholar] [CrossRef]
- Khan, M.A.; Suhaib, M.; Ansari, M.A. Investigations on fluid flow and mixing in fractal tree like biomimetic microchannel based on Murray’s law. Chem. Eng. Process. Process Intensif. 2023, 194, 109564. [Google Scholar] [CrossRef]
- Zhu, R.; Jing, D. Numerical study on the discharging performance of a latent heat thermal energy storage system with fractal tree-shaped convergent fins. Renew. Energy 2024, 221, 119726. [Google Scholar] [CrossRef]
- Zhu, R.; Jing, D. Numerical study on thermal and melting performances of a horizontal latent heat storage unit with branched tree-like convergent fins. J. Energy Storage 2023, 62, 106889. [Google Scholar] [CrossRef]
- Qi, P.; Jing, D. Experimental and numerical study on the hydrothermal performances of a mirror Y-shaped convergent mini-channel heat sink. Case Stud. Therm. Eng. 2024, 53, 103966. [Google Scholar] [CrossRef]
- Liu, F.; Zhu, R.; Jing, D. Hydraulic and thermal performances of tree-like convergent microchannel heat sinks. Fractals 2022, 30, 2250096. [Google Scholar] [CrossRef]
- Chakraborty, S.; Mondal, N.; Bakli, C. Passive building cooling using tree-shaped converging microchannel nets. In AIP Conference Proceedings, Proceedings of the 2nd International Conference on Recent Advances in Fluid and Thermal Sciences 2020 (iCRAFT2020), Dubai, United Arab Emirates, 19–21 March 2021; AIP Publishing: Melville, NY, USA, 2023; Volume 2584, p. 050001. [Google Scholar]
- Murray, C.D. The physiological principle of minimum work: I. The vascular system and the cost of blood volume. Proc. Natl. Acad. Sci. USA 1926, 12, 207–214. [Google Scholar] [CrossRef]
- Miguel, A.F. Fluid flow in a porous tree-shaped network: Optimal design and extension of Hess–Murray’s law. Phys. A Stat. Mech. Its Appl. 2015, 423, 61–71. [Google Scholar]
- Patankar, N.A.; Hu, H.H. Numerical simulation of electroosmotic flow. Anal. Chem. 1998, 70, 1870–1881. [Google Scholar] [CrossRef] [PubMed]
- Kang, Y.; Yang, C.; Huang, X. Electroosmotic flow in a capillary annulus with high zeta potentials. J. Colloid Interface Sci. 2002, 253, 285–294. [Google Scholar] [CrossRef] [PubMed]
- Yuan, S.; Zhou, M.; Liu, X.; Jiang, B. Effect of pressure-driven flow on electroosmotic flow and electrokinetic mass transport in microchannels. Int. J. Heat Mass Transf. 2023, 206, 123925. [Google Scholar] [CrossRef]
- Ng, C.O.; Qi, C. Electroosmotic flow of a power-law fluid in a non-uniform microchannel. J. Non-Newton. Fluid Mech. 2014, 208, 118–125. [Google Scholar]
- Dutta, P.; Beskok, A. Analytical solution of combined electroosmotic/pressure driven flows in two-dimensional straight channels: Finite Debye layer effects. Anal. Chem. 2001, 73, 1979–1986. [Google Scholar] [CrossRef] [PubMed]
- Miguel, A.F.; Rocha, L.A. Tree-Shaped Fluid Flow and Heat Transfer; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar]
- Yu, H.; Zhang, J.; Zhang, S.; Han, Z. Bionic Struct. Mater. Inspired By Plant Leaves: A comprehensive review for innovative problem-solving. Prog. Mater. Sci. 2023, 139, 101181. [Google Scholar] [CrossRef]







| Parameters | Symbol | Value |
|---|---|---|
| Branch convergence | α | 0.4–1 |
| Level convergence | κ | 0.7–1 |
| Length ratio | λ | 0.5–1 |
| Branching number | N | 2, 3, 4 |
| Branching level | m | 0, 1, 2, 3 |
| Channel height | H (μm) | 150 |
| Branch angle | β (°) | 60 |
| Total channel volume | V (μm3) | 3 108 |
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Zeta potential | ζ | −50 | mV |
| Fluid density | ρ | 996 | kg/m3 |
| Dynamic viscosity | μ | 1 10−3 | Pa·s |
| Relative permittivity | εr | 80 | / |
| Electric conductivity | σ | 5.5 10−6 | S/m |
| Diffusion coefficient | Dc | ||
| Bulk ionic concentration | c0 | 1 | mol/m3 |
| No. i | Grid Number | )] | Computing Time | |||
|---|---|---|---|---|---|---|
| 0 | 51,183 | 7.3401 | / | 7.9226 | / | 3 min 39 s |
| 1 | 351,336 | 7.2484 | 1.249% | 7.7683 | 1.948% | 9 min 25 s |
| 2 | 401,948 | 7.1848 | 0.877% | 7.6458 | 1.577% | 12 min 41 s |
| 3 | 1,350,140 | 7.1614 | 0.326% | 7.6277 | 0.237% | 40 min 35 s |
| 4 | 1,697,420 | 7.1643 | 0.040% | 7.6358 | 0.106% | 1 h 26 min 52 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, D.; Qi, P. The Optimal Branch Width Convergence Ratio to Maximize the Transport Efficiency of the Combined Electroosmotic and Pressure-Driven Flow within a Fractal Tree-like Convergent Microchannel. Fractal Fract. 2024, 8, 279. https://doi.org/10.3390/fractalfract8050279
Jing D, Qi P. The Optimal Branch Width Convergence Ratio to Maximize the Transport Efficiency of the Combined Electroosmotic and Pressure-Driven Flow within a Fractal Tree-like Convergent Microchannel. Fractal and Fractional. 2024; 8(5):279. https://doi.org/10.3390/fractalfract8050279
Chicago/Turabian StyleJing, Dalei, and Peng Qi. 2024. "The Optimal Branch Width Convergence Ratio to Maximize the Transport Efficiency of the Combined Electroosmotic and Pressure-Driven Flow within a Fractal Tree-like Convergent Microchannel" Fractal and Fractional 8, no. 5: 279. https://doi.org/10.3390/fractalfract8050279





