On Perturbative Methods for Analyzing Third-Order Forced Van-der Pol Oscillators
Abstract
:1. Introduction
- With respect to the first objective, we seek to find some approximate solutions to Equation (2) using two perturbative methods, known as, the Krylov–Bogoliúbov-Mitropólsky (KBM) method (KBMM) and the multiple scales method (MSM).
- With respect to the second objective, we apply a linear suitable transformation to obtain an approximate solution to the forced jerk oscillatory Equation (3).
- Furthermore, the proposed problem is analyzed numerically via the fourth-order Runge–Kutta (RK4) method. Then, a comparison between the accuracy of all the obtained approximations is considered.
2. Methodology of Solution
2.1. KBMM for Anatomy Jerk Van-der Pol Oscillatory Equation
2.2. MSM for Anatomy Jerk Van-der Pol Oscillatory Equation
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Coefficients of Equation (19)
References
- Gottlieb, H.P.W. Question #38. What is the simplest jerk function that gives chaos? Am. J. Phys. 1996, 64, 525. [Google Scholar]
- Rauch, L.L. Oscillation of a third-order nonlinear autonomous system. In Contributions to the Theory of Nonlinear Oscillations; Lefschetz, S., Ed.; Princeton University Press: Princeton, NJ, USA, 1950; Volume 20, p. 39. [Google Scholar]
- Stirangarajan, H.R.; Dasarathy, B.V. Study of third-order nonlinear systems-variation of parameters approach. J. Sound Vib. 1975, 40, 173. [Google Scholar] [CrossRef]
- Gottlieb, H.P.W. Harmonic balance approach to periodic solutions of non-linear Jerk equations. J. Sound Vib. 2004, 271, 671. [Google Scholar] [CrossRef] [Green Version]
- Kenmogne, F.; Noubissie, S.; Ndombou, G.B.; Tebue, E.T.; Sonna, A.V.; Yemélé, D. Dynamics of two models of driven extended jerk oscillators: Chaotic pulse generations and application in engineering. Chaos Solitons Fractals 2021, 152, 111291. [Google Scholar] [CrossRef]
- El-Dib, Y.O. The simplest approach to solving the cubic nonlinear jerk oscillator with the non-perturbative method. Math. Methods Appl. Sci. 2022, 45, 5165. [Google Scholar] [CrossRef]
- El-Dib, Y.O. An Efficient Approach to solving fractional Van der Pol–Duffing jerk oscillator. Commun. Theor. Phys. 2022, 74, 105006. [Google Scholar] [CrossRef]
- Gottlieb, H.P.W. Harmonic balance approach to limit cycles for nonlinear Jerk equations. J. Sound Vib. 2006, 297, 243. [Google Scholar] [CrossRef] [Green Version]
- Alam, M.S.; Haque, M.E.; Hossain, M.B. A new analytical technique to find periodic solutions of non-linear systems. Int. J. Non-Linear Mech. 2007, 42, 1035. [Google Scholar] [CrossRef]
- Karahan, M.M.F. Approximate Solutions for the Nonlinear Third-Order Ordinary Differential Equations. Z. Naturforsch. 2017, 72, 547. [Google Scholar] [CrossRef]
- Ramos, J.I. Approximate methods based on order reduction for the periodic solutions of nonlinear third-order ordinary differential equations. Appl. Math. Comput. 2010, 215, 4304. [Google Scholar] [CrossRef]
- Feng, S.-D.; Chen, L.-Q. Homotopy Analysis Approach to Periodic Solutions of a Nonlinear Jerk Equation. Chin. Phys. Lett. 2009, 26, 124501. [Google Scholar]
- Liu, C.-S.; Chang, J.-R. The periods and periodic solutions of nonlinear jerk equations solved by an iterative algorithm based on a shape function method. Appl. Math. Lett. 2020, 102, 10615. [Google Scholar] [CrossRef]
- Ma, X.; Wei, L.; Guo, Z. He’s homotopy perturbation method to periodic solutions of nonlinear jerk equations. J. Sound Vib. 2008, 314, 217. [Google Scholar] [CrossRef]
- Salas, A.H.; Abu Hammad, M.; Alotaibi, B.M.; El-Sherif, L.S.; El-Tantawy, S.A. Analytical and Numerical Approximations to Some Coupled Forced Damped Duffing Oscillators. Symmetry 2022, 14, 2286. [Google Scholar] [CrossRef]
- Alhejaili, W.; Salas, A.H.; El-Tantawy, S.A. Approximate solution to a generalized Van der Pol equation arising in plasma oscillations. AIP Adv. 2022, 12, 105104. [Google Scholar] [CrossRef]
- Alyousef, H.A.; Alharthi, M.R.; Salas, A.H.; El-Tantawy, S.A. Optimal analytical and numerical approximations to the (un)forced (un)damped parametric pendulum oscillator. Commun. Theor. Phys. 2022, 74, 105002. [Google Scholar] [CrossRef]
- Alam, M.S.; Akbar, M.A.; Islam, M.Z. A general form of Krylov–Bogoliubov–Mitropolskii methodfor solving nonlinear partial differential equations. J. Sound Vib. 2005, 285, 173–185. [Google Scholar] [CrossRef]
- Ramnath, R.V.; Sandri, G. A generalized multiple scales approach to a class of linear differential equations. J. Math. Anal. Appl. 1969, 28, 339. [Google Scholar] [CrossRef] [Green Version]
- Kumar, M.; Varshney, P. Numerical Simulation of Van der Pol Equation Using Multiple Scales Modified Lindstedt–Poincare Method. Proc. Natl. Acad. Sci. India Sect. A Phys. 2021, 91, 55–65. [Google Scholar] [CrossRef]
- Razzak, M.A.; Alam, M.Z.; Sharif, M.N. Modified multiple time scale method for solving strongly nonlinear damped forced vibration systems. Results Phys. 2018, 8, 231. [Google Scholar] [CrossRef]
- Rajagopal, K.; Kingni, S.T.; Kuiate, G.F.; Tamba, V.K.; Pham, V.-T. Autonomous Jerk Oscillator with Cosine Hyperbolic Nonlinearity: Analysis, FPGA Implementation, and Synchronization. Adv. Math. 2018, 2018, 7273531. [Google Scholar] [CrossRef]
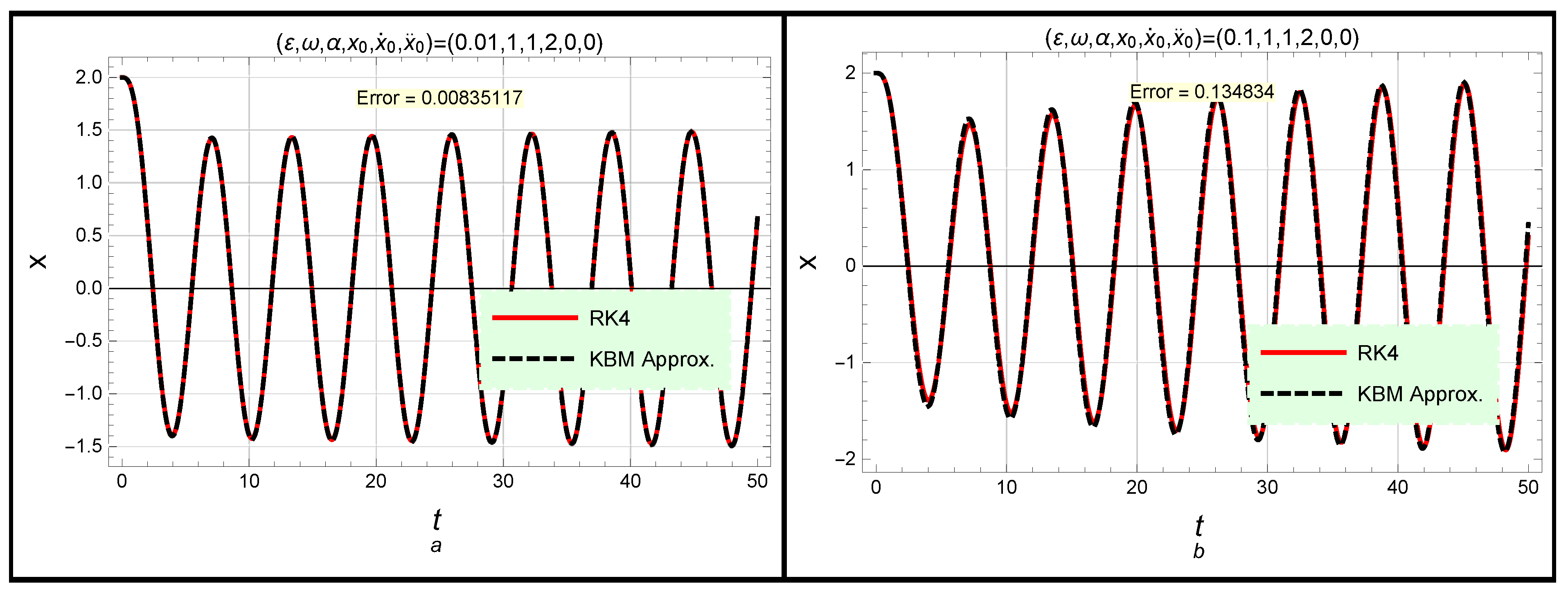



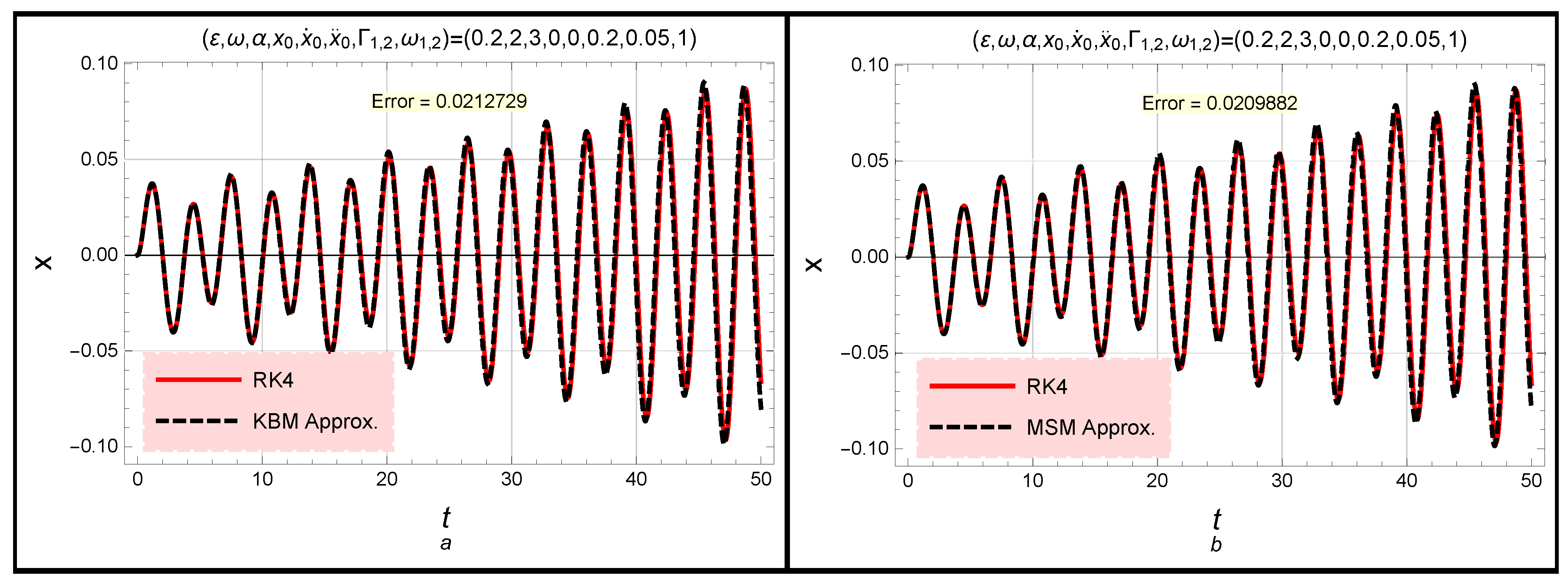
| The Parameter | |
|---|---|
| 0.134834 | |
| 0.00835117 | |
| 0.0368 | |
| 0.0441987 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhejaili, W.; Salas, A.H.; Tag-Eldin, E.; El-Tantawy, S.A. On Perturbative Methods for Analyzing Third-Order Forced Van-der Pol Oscillators. Symmetry 2023, 15, 89. https://doi.org/10.3390/sym15010089
Alhejaili W, Salas AH, Tag-Eldin E, El-Tantawy SA. On Perturbative Methods for Analyzing Third-Order Forced Van-der Pol Oscillators. Symmetry. 2023; 15(1):89. https://doi.org/10.3390/sym15010089
Chicago/Turabian StyleAlhejaili, Weaam, Alvaro H. Salas, Elsayed Tag-Eldin, and Samir A. El-Tantawy. 2023. "On Perturbative Methods for Analyzing Third-Order Forced Van-der Pol Oscillators" Symmetry 15, no. 1: 89. https://doi.org/10.3390/sym15010089







