A Numerical Study of the Performance of Point Absorber Wave Energy Converters
Abstract
:1. Introduction
2. Numerical Model
2.1. Computational Domain and Mesh
2.2. Flow Settings
2.3. Mesh Independence Study and Validation
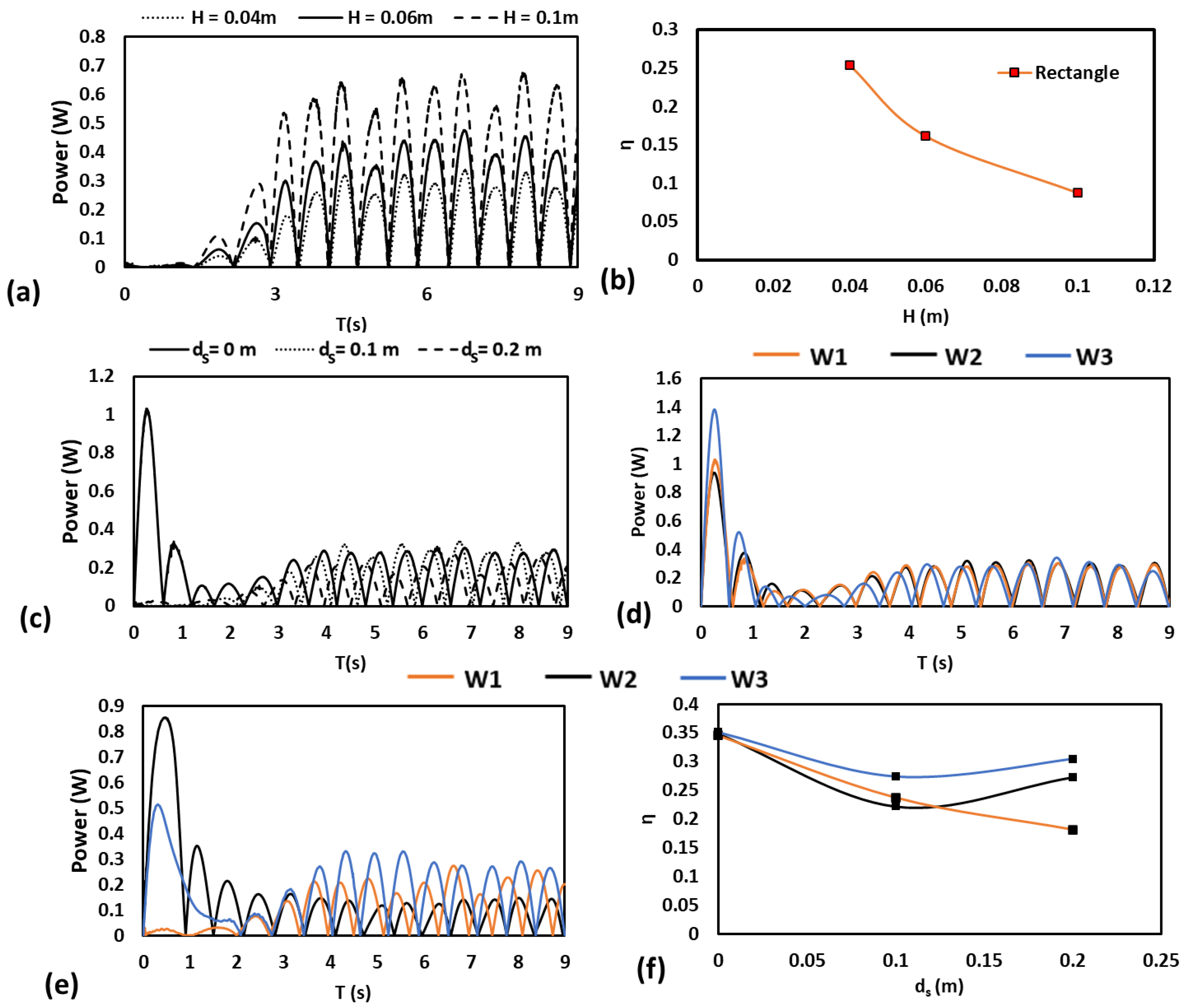
3. Results and Discussion
3.1. Effect of Submergence Depth
3.2. Effect of WEC Shape
3.3. Effect of Wave Height
3.4. Effect of Spring Constant
4. Conclusions
- The spring constant reduces the efficiency of the WEC but develops a stable floating movement of the submerged WEC.
- Submergence increases with increased power absorption but reduces the conversion efficiency.
- A trapezoidal fin provides higher efficiency than either a rectangular box or a circular cylinder.
- With an increase in wave height, the power absorption increases, but the efficiency decreases.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- López, I.; Andreu, J.; Ceballos, S.; De Alegría, I.M.; Kortabarria, I. Review of wave energy technologies and the necessary power-equipment. Renew. Sustain. Energy Rev. 2013, 27, 413–434. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, H.; Hu, M.; Meng, G.; Wen, C. A Review of Offshore Wave Energy Extraction System. Adv. Mech. Eng. 2013, 5, 623020. [Google Scholar] [CrossRef]
- He, G.; Luan, Z.; Zhang, W.; He, R.; Liu, C.; Yang, K.; Yang, C.; Jing, P.; Zhang, Z. Review on research approaches for multi-point absorber wave energy converters. Renew. Energy 2023, 218, 119237. [Google Scholar] [CrossRef]
- Ahamed, R.; Mckee, K.; Howard, I. Advancements of wave energy converters based on power take off (PTO) systems: A review. Ocean. Eng. 2020, 204, 107248. [Google Scholar] [CrossRef]
- Bracco, G.; Cagninei, A.; Giorcelli, E.; Mattiazzo, G.; Poggi, D.; Raffero, M. Experimental validation of the ISWEC wave to PTO model. Ocean Eng. 2016, 120, 40–51. [Google Scholar] [CrossRef]
- Sergiienko, N.Y.; Cazzolato, B.S.; Ding, B.; Hardy, P.; Arjomandi, M. Performance comparison of the floating and fully submerged quasi-point absorber wave energy converters. Renew. Energy 2017, 108, 425–437. [Google Scholar] [CrossRef]
- Mciver, P.; Evans, D.V. The occurrence of negative added mass in free-surface problems involving submerged oscillating bodies. J. Eng. Math. 1984, 18, 7–22. [Google Scholar] [CrossRef]
- Davis, J.P. Wave energy absorption by the Bristol Cylinder. Linear and non-linear effects. Proc. Inst. Civ. Eng. Part 2 Res. Theory 1990, 89, 317–340. [Google Scholar] [CrossRef]
- Heikkinen, H.; Lampinen, M.J.; Böling, J. Analytical study of the interaction between waves and cylindrical wave energy converters oscillating in two modes. Renew. Energy 2013, 50, 150–160. [Google Scholar] [CrossRef]
- Tran, N.; Sergiienko, N.Y.; Cazzolato, B.S.; Ghayesh, M.H.; Arjomandi, M. Design considerations for a three-tethered point absorber wave energy converter with nonlinear coupling between hydrodynamic modes. Ocean Eng. 2022, 254, 111351. [Google Scholar] [CrossRef]
- Ren, B.; He, M.; Dong, P.; Wen, H. Nonlinear simulations of wave-induced motions of a freely floating body using WCSPH method. Appl. Ocean. Res. 2015, 50, 1–12. [Google Scholar] [CrossRef]
- Ropero-Giralda, P.; Crespo, A.J.C.; Coe, R.G.; Tagliafierro, B.; Domínguez, J.M.; Bacelli, G.; Gómez-Gesteira, M. Modelling a heaving point-absorber with a closed-loop control system using the dualsphysics code. Energies 2021, 14, 760. [Google Scholar] [CrossRef]
- He, M.; Gao, X.; Xu, W.; Ren, B.; Wang, H. Potential application of submerged horizontal plate as a wave energy breakwater: A 2D study using the WCSPH method. Ocean Eng. 2019, 185, 27–46. [Google Scholar] [CrossRef]
- Zheng, X.; Chen, G.; Cao, W.; Xu, H.; Zhao, R.; Xu, Q.; Kramer, M.; Le Touzé, D.; Borthwick, A.G.L.; Li, Y. On the energy conversion characteristics of a top-mounted pitching absorber by using smoothed particle hydrodynamics. Energy Convers. Manag. 2021, 250, 114893. [Google Scholar] [CrossRef]
- Palm, J.; Eskilsson, C. Mooring systems with submerged buoys: Influence of buoy geometry and modelling fidelity. Appl. Ocean Res. 2020, 102, 102302. [Google Scholar] [CrossRef]
- Anbarsooz, M.; Passandideh-Fard, M.; Moghiman, M. Numerical simulation of a submerged cylindrical wave energy converter. Renew. Energy 2014, 64, 132–143. [Google Scholar] [CrossRef]
- Prakash, R.; Rathaur, R.; Gupta, S.; Ghosh, S.; Kumar, D.; Agarwal, R.; Vatsa, S.K.; Khandige, M. A numerical study on float design for wave energy converter. Ocean Eng. 2022, 264, 112410. [Google Scholar] [CrossRef]
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; World Scientific Publishing Co. Pte. Ltd.: Singapore, 1984. [Google Scholar] [CrossRef]
- Higuera, P.; Lara, J.L.; Losada, I.J. Realistic wave generation and active wave absorption for Navier-Stokes models. Application to OpenFOAM®. Coast. Eng. 2013, 71, 102–118. [Google Scholar] [CrossRef]
- Gourma, M.; Verdin, P. Two-phase slug flows in helical pipes: Slug frequency alterations and helicity fluctuations. Int. J. Multiph. Flow. 2016, 86, 10–20. [Google Scholar] [CrossRef]
- Gourma, M.; Verdin, P. Nature and magnitude of operating forces in a horizontal bend conveying gas-liquid slug flows. J. Pet. Sci. Eng. 2020, 190, 107062. [Google Scholar] [CrossRef]
- Ibnu Syihab, A.B.M.; Verdin, P.G.; Wright, R.M.; Piper, A.T.; Rivas Casado, M. Computational fluid dynamics simulations of water flow on a studded upstream eel pass. River Res. Appl. 2021, 37, 1279–1293. [Google Scholar] [CrossRef]
- Devolder, B.; Troch, P.; Rauwoens, P. Accelerated numerical simulations of a heaving floating body by coupling a motion solver with a two-phase fluid solver. Comput. Math. Appl. 2019, 77, 1605–1625. [Google Scholar] [CrossRef]
- Kissling, K.; Springer, J.; Jasak, H.; Schutz, S.; Urban, K.; Piesche, M. A Coupled Pressure Based Solution Algorithm Based on the Volume-of-Fluid Approach for Two or More Immiscible Fluids. In Proceedings of the V European Conference on Computational Fluid Dynamics ECCOMAS CFD 2010, Lisbon, Portugal, 14–17 June 2010. [Google Scholar]
- Saghafian, M.; Stansby, P.K.; Saidi, M.S.; Apsley, D.D. Simulation of turbulent flows around a circular cylinder using nonlinear eddy-viscosity modelling: Steady and oscillatory ambient flows. J. Fluids Struct. 2003, 17, 1213–1236. [Google Scholar] [CrossRef]
- Jamalabadi, M.Y.A.; Ho-Huu, V.; Nguyen, T.K. Optimal design of circular baffles on sloshing in a rectangular tank horizontally coupled by structure. Water 2018, 10, 1504. [Google Scholar] [CrossRef]
- Sheng, W.; Alcorn, R.; Lewis, T. Physical modelling of wave energy converters. Ocean. Eng. 2014, 84, 29–36. [Google Scholar] [CrossRef]
- Jin, S.; Patton, R.J.; Guo, B. Enhancement of wave energy absorption efficiency via geometry and power take-off damping tuning. Energy 2019, 169, 819–832. [Google Scholar] [CrossRef]












| Shape | Density (kg/m3) | Wave Height (m) | Spring Stiffness (k) | Submergence Depth (ds) | Time Period (s) |
|---|---|---|---|---|---|
| Rectangular | 1000 | 0.04, 0.06, 0.1 | 0, 50, 100 | 0, 0.1, 0.2 | 1.2 |
| Circular cylindrical | 1000 | 0.04 | 50 | 0, 0.1, 0.2 | 1.2 |
| Trapezoidal fin | 1000 | 0.04 | 50 | 0, 0.1, 0.2 | 1.2 |
| Case | Coarse | Medium | Fine | Extra-Fine |
|---|---|---|---|---|
| Number of cells | 107,686 | 115,660 | 126,676 | 140,320 |
| Min. cell size (mm) | 0.015 | 0.010 | 0.005 | 0.002 |
| Max. disp. z/d | 0.071 | 0.071 | 0.060 | 0.060 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rathaur, R.; Verdin, P.G.; Ghosh, S. A Numerical Study of the Performance of Point Absorber Wave Energy Converters. Appl. Sci. 2024, 14, 4039. https://doi.org/10.3390/app14104039
Rathaur R, Verdin PG, Ghosh S. A Numerical Study of the Performance of Point Absorber Wave Energy Converters. Applied Sciences. 2024; 14(10):4039. https://doi.org/10.3390/app14104039
Chicago/Turabian StyleRathaur, Ranjana, Patrick G. Verdin, and Sumana Ghosh. 2024. "A Numerical Study of the Performance of Point Absorber Wave Energy Converters" Applied Sciences 14, no. 10: 4039. https://doi.org/10.3390/app14104039






