Modeling and Mitigating Output-Dependent Modulation in Current-Steering DAC Based on Differential-Quad Switching Scheme
Abstract
:1. Introduction
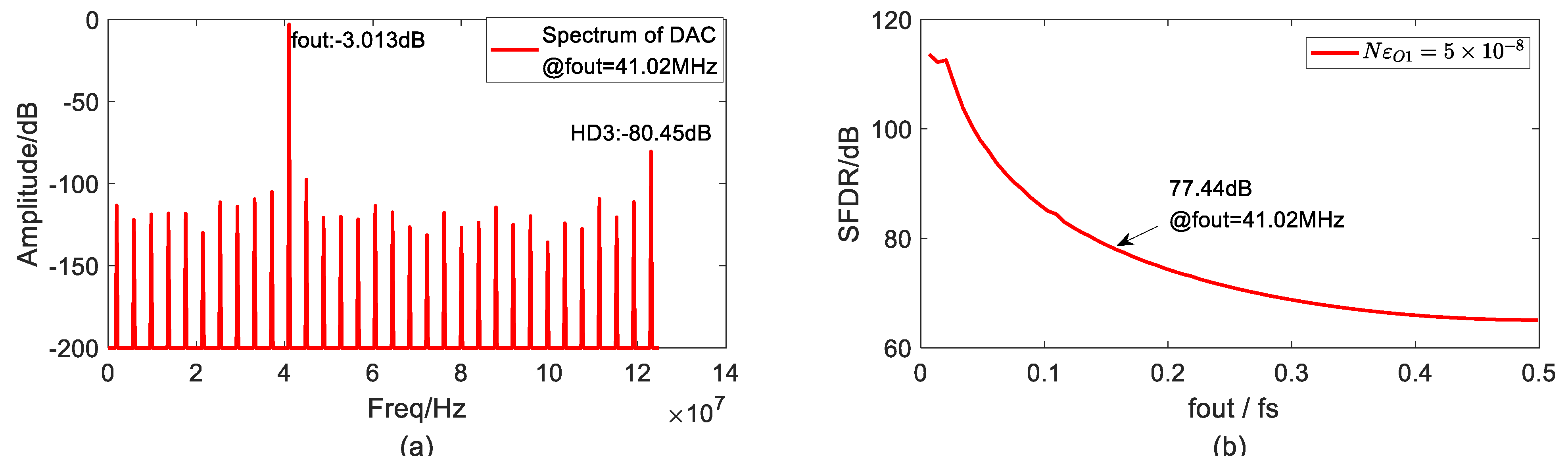
2. Output-Dependent Modulation Based on DQS Structure
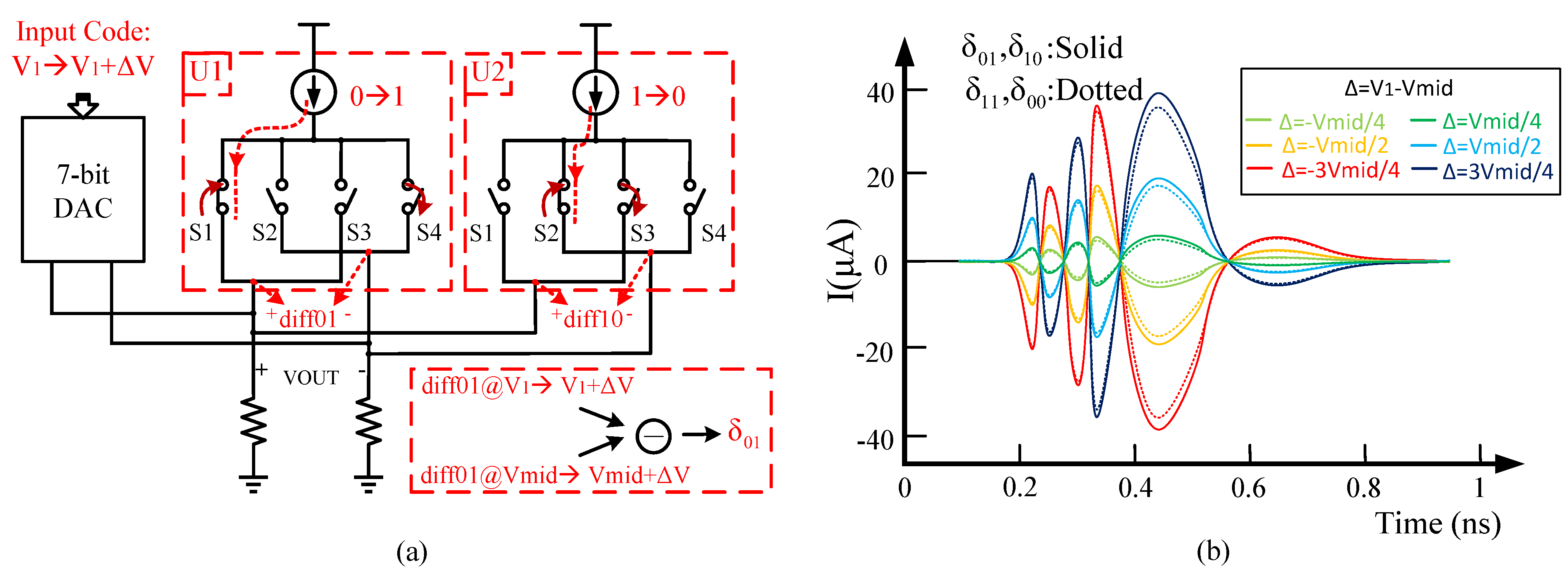
2.1. Opposite-Side Switching Errors (OSEs)
- (1)
- Assume that 11 (00) and 01 (10) have the same output dependency.
- (2)
- Ignore the influence of initial and final output voltages on errors; the OSEs are solely related to output transition.
2.2. Same-Side Switching Errors (SSEs)
2.3. Boundary Effect Errors (BEEs)
3. DAC Architecture and Implementation of Circuits
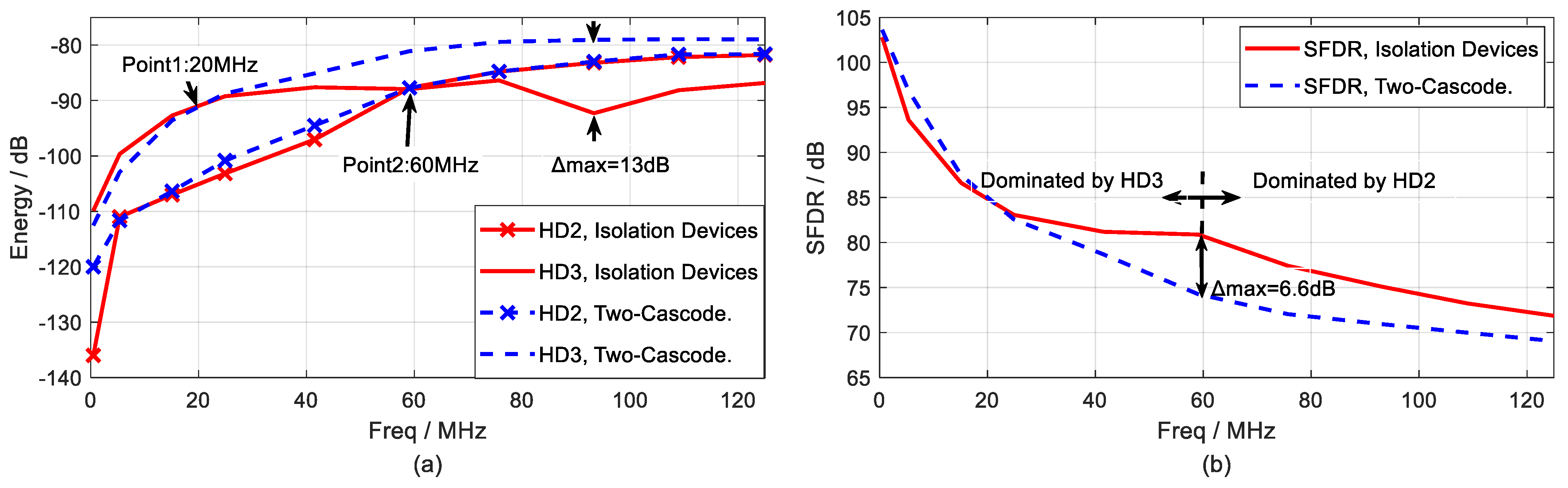
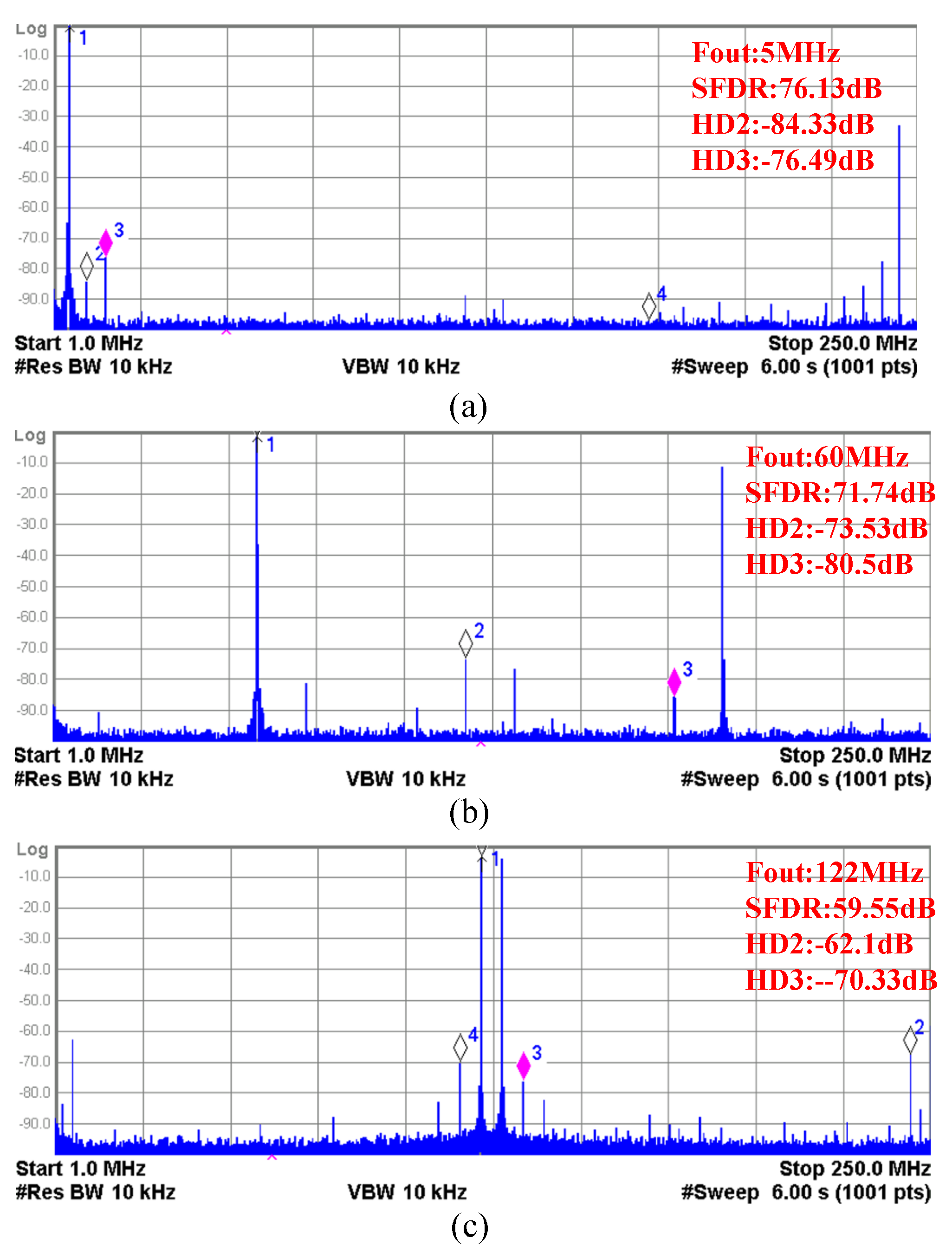
4. Measurement Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- van den Bosch, A.; Steyaert, M.; Sansen, W. SFDR-bandwidth limitations for high speed high resolution current steering CMOS D/A converters. In Proceedings of the ICECS’99—Proceedings of ICECS ’99. 6th IEEE International Conference on Electronics, Circuits and Systems (Cat. No.99EX357), Paphos, Cyprus, 5–8 September 1999; Volume 3, pp. 1193–1196. [Google Scholar] [CrossRef]
- Luschas, S.; Lee, H.S. Output impedance requirements for DACs. In Proceedings of the 2003 International Symposium on Circuits and Systems, Bangkok, Thailand, 25–28 May 2003; Volume 1. [Google Scholar] [CrossRef]
- Chen, T.; Gielen, G. Modelling of the impact of the current source output impedance on the SFDR of current-steering CMOS D/A converters. In Proceedings of the 2004 IEEE International Symposium on Circuits and Systems (ISCAS), Vancouver, BC, Canada, 23–26 May 2004; Volume 1. [Google Scholar] [CrossRef]
- Galton, I. Why Dynamic-Element-Matching DACs Work. IEee Trans. Circuits Syst. II Express Briefs 2010, 57, 69–74. [Google Scholar] [CrossRef]
- Lee, D.H.; Kuo, T.H.; Wen, K.L. Low-Cost 14-Bit Current-Steering DAC With a Randomized Thermometer-Coding Method. IEEE Trans. Circuits Syst. II Express Briefs 2009, 56, 137–141. [Google Scholar] [CrossRef]
- Tong, X.; Liu, D. High SFDR Current-Steering DAC with Splitting-and-Binary Segmented Architecture and Dynamic-Element-Matching Technique. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 4233–4237. [Google Scholar] [CrossRef]
- Park, S.; Kim, G.; Park, S.C.; Kim, W. A digital-to-analog converter based on differential-quad switching. IEEE J. Solid-State Circuits 2002, 37, 1335–1338. [Google Scholar] [CrossRef]
- Schafferer, B.; Adams, R. A 3 V CMOS 400 mW 14b 1.4GS/s DAC for multi-carrier applications. In Proceedings of the 2004 IEEE International Solid-State Circuits Conference (IEEE Cat. No.04CH37519), San Francisco, CA, USA, 15–19 February 2004; Volume 1, pp. 360–532. [Google Scholar] [CrossRef]
- Engel, G.; Kuo, S.; Rose, S. A 14b 3/6GHz current-steering RF DAC in 0.18 μm CMOS with 66 dB ACLR at 2.9 GHz. In Proceedings of the 2012 IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 19–23 February 2012; pp. 458–460. [Google Scholar] [CrossRef]
- Liu, M.; Zhu, Z.; Yang, Y. A High-SFDR 14-bit 500 MS/s Current-Steering D/A Converter in 0.18 μm CMOS. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2015, 23, 3148–3152. [Google Scholar] [CrossRef]
- Wang, F.; Wang, Z.; Liu, J.; Yu, F. A 14-Bit 3-GS/s DAC Achieving SFDR >63dB Up to 1.4 GHz With Random Differential-Quad Switching Technique. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 879–883. [Google Scholar] [CrossRef]
- Lai, L.; Li, X.; Fu, Y.; Liu, Y.; Yang, H. Demystifying and Mitigating Code-Dependent Switching Distortions in Current-Steering DACs. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 68–81. [Google Scholar] [CrossRef]
- Tseng, W.H.; Lin, W.; Hsu, C.W.; Huang, C.Y.; Lin, Y.S.; Huang, H.Y.; Chen, H.; Liao, S.H.; Chen, K.D.; Strange, J.; et al. 17.3 A 14b 16 GS/s Time-Interleaving Oirect-RF Synthesis OAe with T-OEM Achieving −70dBc IM3 up to 7.8 GHz in 7 nm. In Proceedings of the 2023 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 19–23 February 2023; pp. 268–270. [Google Scholar] [CrossRef]
- Kong, D.; Rivas-Rivera, K.; Galton, I. A 600-MS/s DAC with over 87-dB SFDR and 77-dB Peak SNDR Enabled by Adaptive Cancellation of Static and Dynamic Mismatch Error. IEEE J. Solid-State Circuits 2019, 54, 2219–2229. [Google Scholar] [CrossRef]
- Huang, H.Y.; Chen, X.Y.; Kuo, T.H. A 10-GS/s NRZ/Mixing DAC With Switching-Glitch Compensation Achieving SFDR >64/50 dBc over the First/Second Nyquist Zone. IEEE J. Solid-State Circuits 2021, 56, 3145–3156. [Google Scholar] [CrossRef]
- Huang, H.Y.; Chen, X.Y.; Kuo, T.H. A 177 mW 10GS/s NRZ DAC with Switching-Glitch Compensation Achieving > 64 dBc SFDR and <−77 dBc IM3. In Proceedings of the 2020 IEEE Symposium on VLSI Circuits, Honolulu, HI, USA, 16–19 June 2020; pp. 1–2. [Google Scholar] [CrossRef]
- Huang, H.Y.; Kuo, T.H. A 0.07-mm2 162-mW DAC Achieving >65 dBc SFDR and < −70 dBc IM3 at 10 GS/s with Output Impedance Compensation and Concentric Parallelogram Routing. IEEE J. Solid-State Circuits 2020, 55, 2478–2488. [Google Scholar] [CrossRef]
- Lin, C.H.; van der Goes, F.; Westra, J.; Mulder, J.; Lin, Y.; Arslan, E.; Ayranci, E.; Liu, X.; Bult, K. A 12b 2.9GS/s DAC with IM3 ≪-60dBc beyond 1GHz in 65nm CMOS. In Proceedings of the 2009 IEEE International Solid-State Circuits Conference—Digest of Technical Papers, San Francisco, CA, USA, 8–12 February 2009; pp. 74–75, 75a. [Google Scholar] [CrossRef]
- Lin, C.H.; Wong, K.L.J.; Kim, T.Y.; Xie, G.R.; Major, D.; Unruh, G.; Dommaraju, S.R.; Eberhart, H.; Venes, A. A 16b 6GS/S nyquist DAC with IMD <−90 dBc up to 1.9 GHz in 16nm CMOS. In Proceedings of the 2018 IEEE International Solid-State Circuits Conference—(ISSCC), San Francisco, CA, USA, 11–15 February 2018; pp. 360–362. [Google Scholar] [CrossRef]
- Van de Vel, H.; Briaire, J.; Bastiaansen, C.; van Beek, P.; Geelen, G.; Gunnink, H.; Jin, Y.; Kaba, M.; Luo, K.; Paulus, E.; et al. 11.7 A 240 mW 16b 3.2 GS/s DAC in 65 nm CMOS with <−80 dBc IM3 up to 600 MHz. In Proceedings of the 2014 IEEE International Solid-State Circuits Conference Digest of Technical Papers (ISSCC), San Francisco, CA, USA, 9–13 February 2014; pp. 206–207. [Google Scholar] [CrossRef]
- Mercer, D.A. Low-Power Approaches to High-Speed Current-Steering Digital-to-Analog Converters in 0.18-μm CMOS. IEEE J. Solid-State Circuits 2007, 42, 1688–1698. [Google Scholar] [CrossRef]
- Dongmei, Z.; Dongbing, F.; Jiangang, S.; Kaicheng, L. Digital static calibration technology used for 400MSPS, 16-bit DAC. In Proceedings of the 2009 IEEE International Conference of Electron Devices and Solid-State Circuits (EDSSC), Xi’an, China, 25–27 December 2009; pp. 91–94. [Google Scholar] [CrossRef]
- Andersson, K.; Vesterbacka, M. Modeling of glitches due to rise/fall asymmetry in current-steering digital-to-analog converters. IEEE Trans. Circuits Syst. I Regul. Pap. 2005, 52, 2265–2275. [Google Scholar] [CrossRef]
- Su, S.; Chen, M.S.W. A 16b 12GS/S single/dual-rate DAC with successive bandpass delta-sigma modulator achieving <−67 dBc IM3 within DC-to-6 GHz tunable passbands. In Proceedings of the 2018 IEEE International Solid-State Circuits Conference—(ISSCC), San Francisco, CA, USA, 11–15 February 2018; pp. 362–364. [Google Scholar] [CrossRef]












| This Work | ISSCC [9] | ISSCC [20] | VLSI [10] | JSSC [15] | ISSCC [19] | ISSCC [24] | |
|---|---|---|---|---|---|---|---|
| Resolution (bit) | 16 | 14 | 16 | 14 | 14 | 16 | 16 |
| Process (nm) | 180 | 180 | 65 | 180 | 28 | 16 | 65 |
| Supply (V) | 1.8/3.3 | 1.8/3 | 1.2/3.3 | 3.3 | 1.1 | 1.0/3.3 | - |
| (MS/s) | 250 | 2900 | 3200 | 500 | 10,000 | 6000 | 12,000 |
| Area (mm2) | 6.55 | 4 | - | 0.55 | 0.1 | 0.52 | 5 |
| DNL/INL(LSB) | ±2/±4 | - | - | - | - | -/±0.25 | - |
| (dB) | 76.13 | 84 | 84 | 83.7 | 74.3 | 88 | 76 |
| (dB) | 59.55 | 52 | 58 | 68.9 | 64.5 | 67 | 59 |
| [6] (GHz/mW) | |||||||
| 95.4 | 136.5 | 873.8 | 121 | 925.6 | 1123 | 446.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Zhang, Z.; Shan, Y.; Lang, L.; Dong, Y. Modeling and Mitigating Output-Dependent Modulation in Current-Steering DAC Based on Differential-Quad Switching Scheme. Electronics 2024, 13, 1992. https://doi.org/10.3390/electronics13101992
Sun Y, Zhang Z, Shan Y, Lang L, Dong Y. Modeling and Mitigating Output-Dependent Modulation in Current-Steering DAC Based on Differential-Quad Switching Scheme. Electronics. 2024; 13(10):1992. https://doi.org/10.3390/electronics13101992
Chicago/Turabian StyleSun, Yingchao, Zhenwei Zhang, Yi Shan, Lili Lang, and Yemin Dong. 2024. "Modeling and Mitigating Output-Dependent Modulation in Current-Steering DAC Based on Differential-Quad Switching Scheme" Electronics 13, no. 10: 1992. https://doi.org/10.3390/electronics13101992






