An Ad Hoc Procedure for Testing Serial Correlation in Spatial Fixed-Effects Panels
Abstract
:1. Introduction
1.1. Literature Review and Background
2. The Model
Eliminating Fes by Transformation
3. Testing for Serial Correlation
4. Monte Carlo Experiments
5. Illustrations
5.1. Italian Insurance
5.2. Indonesian Rice Farming
5.3. Cigarettes
6. Discussion, Limitations and Directions for Future Research
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ML | maximum likelihood |
| GM | generalized moments |
| FE | fixed effects |
| RE | random effects |
| LM | Lagrange multiplier (test) |
| LR | likelihood ratio (test) |
| OLS | ordinary least squares |
| GLS | generalized least squares |
| OD | (forward) orthogonal deviations |
| SAR | spatially autoregressive (model) |
| SEM | spatial error model |
Appendix A. Robustness Checks
Appendix A.1. Serial-Spatial Alternative Specification
| 0 | 0.058 | 0.050 | 0.059 | 0.053 |
| 0.1 | 0.397 | 0.360 | 0.407 | 0.381 |
| 0.2 | 0.929 | 0.920 | 0.927 | 0.919 |
| 0.3 | 0.999 | 0.999 | 1.000 | 0.999 |
| 0.4 | 1.000 | 1.000 | 1.000 | 1.000 |
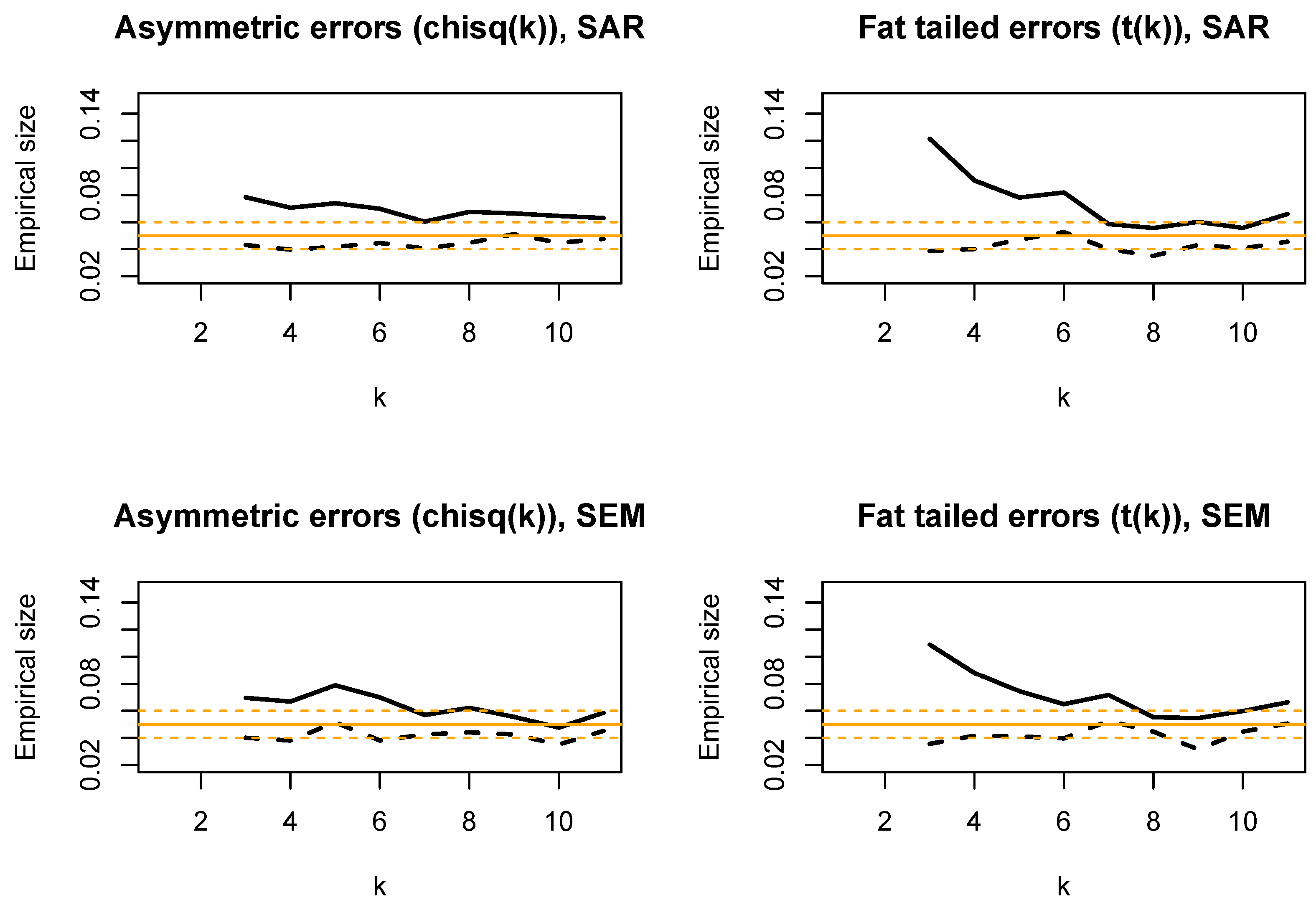
Appendix A.2. Non-Normality
Appendix B. Software Howto
References
- Baltagi, B.; Song, S.; Jung, B.; Koh, W. Testing for serial correlation, spatial autocorrelation and random effects using panel data. J. Econom. 2007, 140, 5–51. [Google Scholar] [CrossRef]
- Debarsy, N.; Ertur, C. Testing for spatial autocorrelation in a fixed effects panel data model. Reg. Sci. Urban Econ. 2010, 40, 453–470. [Google Scholar] [CrossRef]
- Baltagi, B.H.; Yang, Z. Standardized LM tests for spatial error dependence in linear or panel regressions. Econom. J. 2013, 16, 103–134. [Google Scholar] [CrossRef]
- Baltagi, B.H.; Yang, Z. Heteroskedasticity and non-normality robust LM tests for spatial dependence. Reg. Sci. Urban Econ. 2013, 43, 725–739. [Google Scholar] [CrossRef]
- Badi, H.B.; Long, L. Testing for spatial lag and spatial error dependence in a fixed effects panel data model using double length artificial regressions. In Essays in Honor of man Ullah; Emerald Group Publishing Limited: Leeds, UK, 2016; pp. 67–84. [Google Scholar]
- Baltagi, B.H.; Liu, L. Random effects, fixed effects and Hausman’s test for the generalized mixed regressive spatial autoregressive panel data model. Econom. Rev. 2016, 35, 638–658. [Google Scholar] [CrossRef]
- Baltagi, B.H.; Kao, C.; Peng, B. On testing for sphericity with non-normality in a fixed effects panel data model. Stat. Probab. Lett. 2015, 98, 123–130. [Google Scholar] [CrossRef]
- Millo, G. Maximum likelihood estimation of spatially and serially correlated panels with random effects. Comput. Stat. Data Anal. 2014, 71, 914–933. [Google Scholar] [CrossRef]
- Lee, L.; Yu, J. A spatial dynamic panel data model with both time and individual fixed effects. Econom. Theory 2010, 26, 564–597. [Google Scholar] [CrossRef]
- Elhorst, J.P. Spatial Econometrics: From Cross-Sectional Data to Spatial Panels; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Lee, L.f.; Yu, J. Identification of spatial Durbin panel models. J. Appl. Econom. 2016, 31, 133–162. [Google Scholar] [CrossRef]
- Yang, Z. Unified M-estimation of fixed-effects spatial dynamic models with short panels. J. Econom. 2018, 205, 423–447. [Google Scholar] [CrossRef]
- Lee, L.; Yu, J. Spatial panels: Random components versus fixed effects. Int. Econ. Rev. 2012, 53, 1369–1412. [Google Scholar] [CrossRef]
- Griffith, D.A. Some Remarks About the Future of Geographical Analysis: The Journal and the Sub-Discipline. Geogr. Anal. 2021, 53, 19–37. [Google Scholar] [CrossRef]
- Yang, Z. Joint tests for dynamic and spatial effects in short panels with fixed effects and heteroskedasticity. Empir. Econ. 2021, 60, 51–92. [Google Scholar] [CrossRef]
- Wooldridge, J. Econometric Analysis of Cross-Section and Panel Data; MIT Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Lee, L.; Yu, J. Estimation of spatial autoregressive panel data models with fixed effects. J. Econom. 2010, 154, 165–185. [Google Scholar] [CrossRef]
- Elhorst, J. Serial and Spatial error correlation. Econ. Lett. 2008, 100, 422–424. [Google Scholar] [CrossRef]
- Montes-Rojas, G.V. Testing for random effects and serial correlation in spatial autoregressive models. J. Stat. Plan. Inference 2010, 140, 1013–1020. [Google Scholar] [CrossRef]
- Bouayad-Agha, S.; Turpin, N.; Védrine, L. Fostering the Potential Endogenous Development of European Regions: A Spatial Dynamic Panel Data Analysis of the Cohesion Policy on Regional Convergence over the Period 1980–2005; Technical report; TEPP: Bangkok, Thailand, 2012. [Google Scholar]
- Millo, G.; Carmeci, G. Non-life insurance consumption in Italy: A sub-regional panel data analysis. J. Geogr. Syst. 2011, 13, 273–298. [Google Scholar] [CrossRef]
- Millo, G.; Carmeci, G. A Subregional Panel Data Analysis of Life Insurance Consumption in Italy. J. Risk Insur. 2015, 82, 317–340. [Google Scholar] [CrossRef]
- Aravindakshan, A.; Peters, K.; Naik, P.A. Spatiotemporal allocation of advertising budgets. J. Mark. Res. 2012, 49, 1–14. [Google Scholar] [CrossRef]
- Lottmann, F. Explaining Regional Unemployment Differences in Germany: A Spatial Panel Data Analysis; SFB 649 Discussion Paper, No. 2012-026; Humboldt University of Berlin, Collaborative Research Center 649—Economic Risk: Berlin, Germany, 2012. [Google Scholar]
- Kunimitsu, Y.; Kudo, R.; Iizumi, T.; Yokozawa, M. Technological spillover in Japanese rice productivity under long-term climate change: Evidence from the spatial econometric model. Paddy Water Environ. 2015, 14, 131–144. [Google Scholar] [CrossRef]
- Lim-Wavde, K.; Kauffman, R.J.; Kam, T.S.; Dawson, G.S. Do grant funding and pro-environmental spillovers influence household hazardous waste collection? Appl. Geogr. 2019, 109, 102032. [Google Scholar] [CrossRef]
- Olivier, D.; Del Lo, G. Renewable energy drivers in France: A spatial econometric perspective. Reg. Stud. 2022, 56, 1633–1654. [Google Scholar] [CrossRef]
- Sadewo, E.; Hudalah, D.; Antipova, A.; Cheng, L.; Syabri, I. The role of urban transformation on inter-suburban commuting: Evidence from Jakarta metropolitan area, Indonesia. Urban Geogr. 2023, 44, 1628–1653. [Google Scholar] [CrossRef]
- Croissant, Y.; Millo, G. Panel Data Econometrics with R; Wiley: Hoboken, NJ, USA, 2019. [Google Scholar]
- Mátyás, L.; Sevestre, P. The econometrics of Panel Data: Fundamentals and Recent Developments in Theory and Practice; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; Volume 46. [Google Scholar]
- Millo, G.; Piras, G. splm: Spatial panel data models in R. J. Stat. Softw. 2012, 47, 1–38. [Google Scholar] [CrossRef]
- Arellano, M.; Bover, O. Another look at the instrumental variable estimation of error-components models. J. Econom. 1995, 68, 29–51. [Google Scholar] [CrossRef]
- Elhorst, J. Specification and estimation of spatial panel data models. Int. Reg. Sci. Rev. 2003, 26, 244–268. [Google Scholar] [CrossRef]
- Anselin, L.; Le Gallo, J.; Jayet, H. Spatial Panel Econometrics. In Proceedings of the Econometrics of Panel Data, Fundamentals and Recent Developments in Theory and Practice, 3rd ed.; Matyas, L., Sevestre, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 624–660. [Google Scholar]
- Lee, L.; Yu, J. Some recent developments in spatial panel data models. Reg. Sci. Urban Econ. 2010, 40, 255–271. [Google Scholar] [CrossRef]
- Arellano, M. Panel Data Econometrics; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Drukker, D.M. Testing for serial correlation in linear panel-data models. Stata J. 2003, 3, 168–177. [Google Scholar] [CrossRef]
- Baltagi, B.H.; Li, Q. Testing AR (1) against MA (1) disturbances in an error component model. J. Econom. 1995, 68, 133–151. [Google Scholar] [CrossRef]
- Druska, V.; Horrace, W.C. Generalized moments estimation for spatial panel data: Indonesian rice farming. Am. J. Agric. Econ. 2004, 86, 185–198. [Google Scholar] [CrossRef]
- Baltagi, B. Econometric Analysis of Panel Data; John Wiley & Sons: Hoboken, NJ, USA, 2008; Volume 1. [Google Scholar]
- Croissant, Y. Ecdat: Data Sets for Econometrics; R Package Version 0.1-6; R Foundation for Statistical Computing: Vienna, Austria, 2010. [Google Scholar]
- Baltagi, B.H.; Levin, D. Cigarette taxation: Raising revenues and reducing consumption. Struct. Chang. Econ. Dyn. 1992, 3, 321–335. [Google Scholar] [CrossRef]
- Baltagi, B.H.; Griffin, J.M.; Xiong, W. To pool or not to pool: Homogeneous versus heterogeneous estimators applied to cigarette demand. Rev. Econ. Stat. 2000, 82, 117–126. [Google Scholar] [CrossRef]
- Baltagi, B.H.; Griffin, J.M. The econometrics of rational addiction: The case of cigarettes. J. Bus. Econ. Stat. 2001, 19, 449–454. [Google Scholar] [CrossRef]
- Baltagi, B.H.; Li, D. Prediction in the panel data model with spatial correlation. In Advances in Spatial Econometrics; Springer: Berlin/Heidelberg, Germany, 2004; pp. 283–295. [Google Scholar]
- Elhorst, J.P. Unconditional Maximum Likelihood Estimation of Linear and Log-Linear Dynamic Models for Spatial Panels. Geogr. Anal. 2005, 37, 85–106. [Google Scholar] [CrossRef]
- Elhorst, J.P. Matlab software for spatial panels. Int. Reg. Sci. Rev. 2012, 37, 389–405. [Google Scholar] [CrossRef]
- Kelejian, H.H.; Piras, G. An extension of Kelejian’s J-test for non-nested spatial models. Reg. Sci. Urban Econ. 2011, 41, 281–292. [Google Scholar] [CrossRef]
- Debarsy, N.; Ertur, C.; LeSage, J.P. Interpreting dynamic space–time panel data models. Stat. Methodol. 2012, 9, 158–171. [Google Scholar] [CrossRef]
- Kelejian, H.H.; Piras, G. Estimation of spatial models with endogenous weighting matrices, and an application to a demand model for cigarettes. Reg. Sci. Urban Econ. 2014, 46, 140–149. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2012; ISBN 3-900051-12-7. [Google Scholar]
- Shi, W.; Lee, L.f. Spatial dynamic panel data models with interactive fixed effects. J. Econom. 2017, 197, 323–347. [Google Scholar] [CrossRef]
- Long, J.S.; Ervin, L.H. Using heteroscedasticity consistent standard errors in the linear regression model. Am. Stat. 2000, 54, 217–224. [Google Scholar] [CrossRef]
- Croissant, Y.; Millo, G. Panel data econometrics in R: The plm package. J. Stat. Softw. 2008, 27, 1–43. [Google Scholar] [CrossRef]
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0.5 | 0.5 | 0 | 0 | 0.5 | 0.5 | |||
| 0 | 0.5 | 0 | 0.5 | 0 | 0.5 | 0 | 0.5 | |||
| 4 | 0 | 0.062 | 0.061 | 0.064 | 0.066 | 0.068 | 0.069 | 0.063 | 0.061 | |
| 4 | 0.3 | 0.459 | 0.453 | 0.429 | 0.490 | 0.442 | 0.471 | 0.472 | 0.460 | |
| 4 | 0.8 | 0.993 | 0.990 | 0.996 | 0.994 | 0.995 | 0.991 | 0.993 | 0.996 | |
| 10 | 0 | 0.057 | 0.052 | 0.045 | 0.056 | 0.052 | 0.051 | 0.050 | 0.060 | |
| 10 | 0.3 | 0.998 | 0.999 | 0.997 | 0.998 | 0.999 | 0.999 | 0.998 | 0.998 | |
| 10 | 0.8 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | |
| 15 | 0 | 0.067 | 0.052 | 0.041 | 0.054 | 0.044 | 0.055 | 0.054 | 0.051 | |
| 15 | 0.3 | 0.997 | 1.000 | 0.998 | 0.999 | 0.999 | 0.999 | 0.998 | 1.000 | |
| 15 | 0.8 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0.5 | 0.5 | 0 | 0 | 0.5 | 0.5 | |||
| 0 | 0.5 | 0 | 0.5 | 0 | 0.5 | 0 | 0.5 | |||
| 4 | 0 | 0.030 | 0.024 | 0.040 | 0.032 | 0.020 | 0.034 | 0.034 | 0.042 | |
| 4 | 0.3 | 0.276 | 0.274 | 0.253 | 0.272 | 0.257 | 0.262 | 0.271 | 0.261 | |
| 4 | 0.8 | 0.964 | 0.956 | 0.962 | 0.957 | 0.965 | 0.962 | 0.966 | 0.961 | |
| 10 | 0 | 0.049 | 0.057 | 0.037 | 0.044 | 0.039 | 0.049 | 0.049 | 0.038 | |
| 10 | 0.3 | 1.000 | 0.999 | 0.998 | 0.999 | 1.000 | 1.000 | 0.998 | 0.998 | |
| 10 | 0.8 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | |
| 15 | 0 | 0.045 | 0.045 | 0.038 | 0.048 | 0.037 | 0.042 | 0.046 | 0.051 | |
| 15 | 0.3 | 0.997 | 1.000 | 1.000 | 0.999 | 0.999 | 0.998 | 0.999 | 1.000 | |
| 15 | 0.8 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| SEM | |||||||
|---|---|---|---|---|---|---|---|
| Statistic | 703.1 | 22.251 | 35.07 | 5.618 | 0.52 | 9.356 | 4.212 |
| Distribution | z | - | z | z | |||
| p-value | 0 | 0 | 0 | 0 | - | 0 | 0 |
| Computing time | 0.05 | 4.84 | 14.76 | 10.20 | - | 0.68 | 0.42 |
| SAR + SEM | |||||||
| Statistic | - | - | 36.009 | 5.607 | 0.54 | 9.260 | 3.791 |
| Distribution | - | - | z | - | z | z | |
| p-value | - | - | 0 | 0 | - | 0 | 0.0002 |
| Computing time | - | - | 10.79 | 7.60 | - | 1.49 | 0.89 |
| SEM | |||||||
|---|---|---|---|---|---|---|---|
| Statistic | 1129.3 | 7.026 | 4.7306 | 2.129 | 0.087 | 2.005 | 3.085 |
| Distribution | z | - | z | z | |||
| p-value | 0 | 0.008 | 0.029 | 0.033 | - | 0.045 | 0.002 |
| Computing time | 0.15 | 5.41 | 15.40 | 9.95 | - | 1.72 | 2.46 |
| SAR + SEM | |||||||
| Statistic | - | - | 4.985 | 2.220 | 0.089 | 2.153 | 3.125 |
| Distribution | - | - | z | - | z | z | |
| p-value | - | - | 0.0256 | 0.0264 | - | 0.031 | 0.0017 |
| Computing time | - | - | 23.28 | 15.37 | - | 2.64 | 3.96 |
| SEM | |||||||
|---|---|---|---|---|---|---|---|
| Statistic | 12,588.9 | 885.2 | 2034.7 | 286.0 | 0.98 | 86.6 | 89.7 |
| Distribution | z | - | z | z | |||
| p-value | 0 | 0 | 0 | 0 | - | 0 | 0 |
| Computing time | 0.23 | 16.41 | 27.96 | 15.81 | - | 2.94 | 2.74 |
| SAR + SEM | |||||||
| Statistic | - | - | 2031.5 | 293.6 | 0.98 | 90.3 | 95.4 |
| Distribution | - | - | z | - | z | z | |
| p-value | - | - | 0 | 0 | - | 0 | 0 |
| Computing time | - | - | 34.62 | 17.98 | - | 4.33 | 5.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Millo, G. An Ad Hoc Procedure for Testing Serial Correlation in Spatial Fixed-Effects Panels. Mathematics 2024, 12, 1475. https://doi.org/10.3390/math12101475
Millo G. An Ad Hoc Procedure for Testing Serial Correlation in Spatial Fixed-Effects Panels. Mathematics. 2024; 12(10):1475. https://doi.org/10.3390/math12101475
Chicago/Turabian StyleMillo, Giovanni. 2024. "An Ad Hoc Procedure for Testing Serial Correlation in Spatial Fixed-Effects Panels" Mathematics 12, no. 10: 1475. https://doi.org/10.3390/math12101475





