Spacetime Foam: From Entropy and Holography to Infinite Statistics and Nonlocality
Abstract
:There is no excellent beauty that hath not some strangeness in the proportion.— Francis Bacon
1. Introduction
2. Quantum Fluctuations of Spacetime
2.1. Mapping the Geometry of Spacetime
2.2. Models of Spacetime Foam
2.3. Cumulative Effects of Spacetime Fluctuations

3. Probing Quantum Foam with Extragalactic Sources
4. From Quantum Foam to (Holographic Foam) Cosmology
| STF | distance | entropy | energy | matter/ | type of |
| model | fluctuations | bound | density | energy | statistics |
| random- | ordinary | bose / | |||
| walk | fermi | ||||
| holo- | dark | infinite | |||
| graphic | energy |
5. Infinite Statistics and Nonlocality
5.1. Infinite Statistics
5.2. Nonlocality
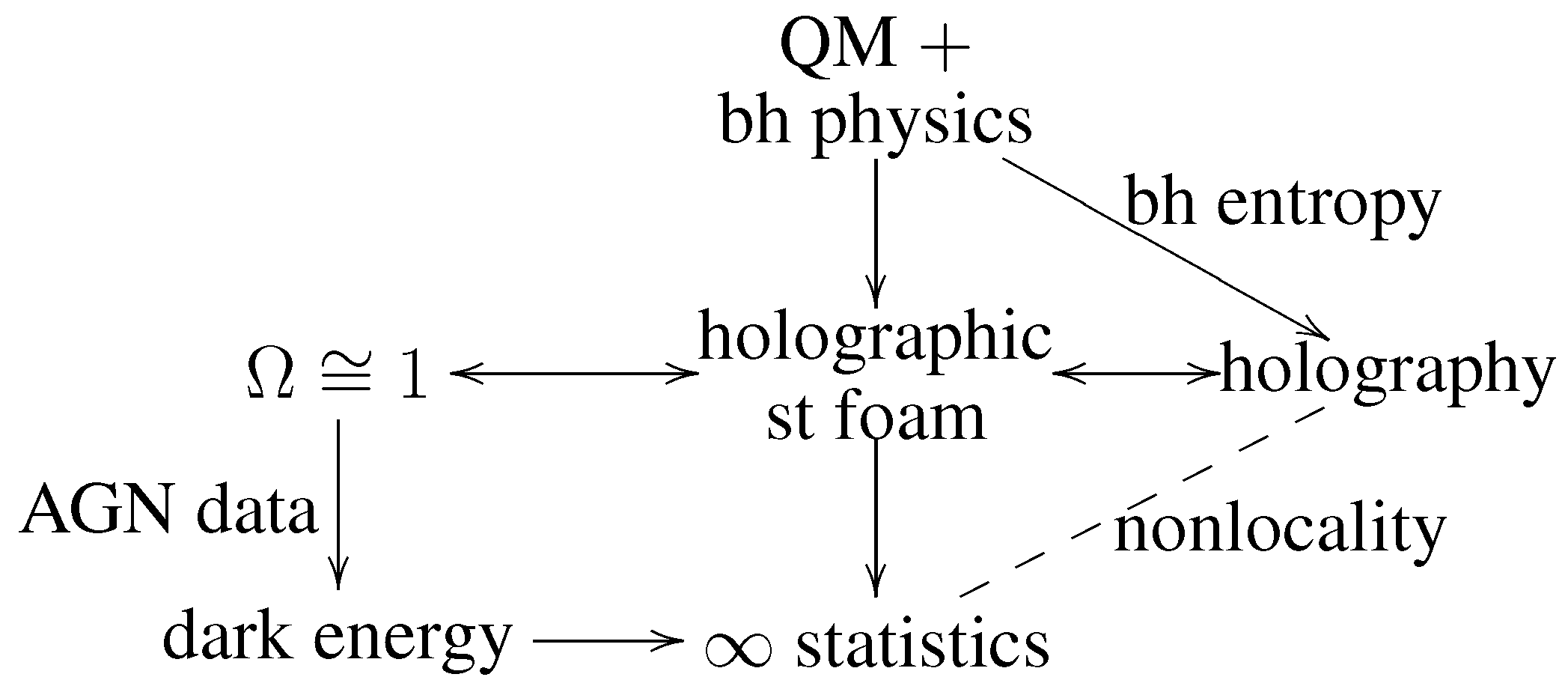
6. Summary, Discussion and Conclusion
7. Acknowledgments
8. Appendix A: Salecker & Wigner’s Gedanken Experiment
9. Appendix B: From Space-time Fluctuations to Black Holes
| distance | clocks | computers |
| measurements | ||
| t | ||
| T | ||
| () |
9.1. Clocks
9.2. Computers
9.3. Black Holes
10. Appendix C: Holographic Principle
11. Appendix D: the Margolus-Levitin Theorem
12. Appendix E: Energy-Momentum Fluctuations
12.1. Modified Dispersion Relations
12.2. Fluctuating Speed of Light
12.3. Unmodified Threshold Energies in Collisions
13. Appendix F: Gamma Ray & Cosmic Ray Phenomenologies
13.1. High Energy γ Rays from Distant GRB
13.2. Ultra-High Energy Cosmic Ray Events
References and Notes
- (a) Wheeler, J.A. Relativity, Groups and Topology; DeWitt, B.S., DeWitt, C.M., Eds.; Gordon & Breach: New York, 1963; p. 315. [Google Scholar] (b) Hawking, S.W.; Page, D.N.; Pope, C.N. Quantum Gravitational Bubbles. Nucl. Phys. 1980, 170, 283–306. [Google Scholar] (c) Ashtekar, A.; Rovelli, C.; Smolin, L. Weaving a Classical Geometry with Quantum Threads. Phys. Rev. Lett. 1992, 69, 237–240. [Google Scholar] (d) Ellis, L.; Mavromatos, N.; Nanopoulos, D.V. String Theory Modifies Quantum Mechanics. Phys. Lett. 1992, B 293, 37–48. [Google Scholar] (e) Garay, L.J. Quantum Gravity and Minimum Length. Int. J. Mod. Phys. 1995, A 10, 145–166. [Google Scholar] (f) Diosi, L.; Lukacs, B. On the Minimum Uncertainty of Space-Time Geodesics. Phys. Lett. 1989, A 142, 331–334. [Google Scholar] (g) Kempf, A.; Mangano, G.; Mann, R.B. Hilbert Space Representation of the Minimum Length Uncertainty Relation. Phys. Rev. 1995, D 52, 1108–1118. [Google Scholar] (h) Hossenfelder, S. The Miminal Length and Large Extra-Dimensions. Mod. Phys. Lett. 2004, A 19, 2727–2744. [Google Scholar]
- (a) Ng, Y.J.; van Dam, H. Limit to Spacetime Measurement. Mod. Phys. Lett. 1994, A 9, 335–340. [Google Scholar] (b) Ng, Y.J.; van Dam, H. Remarks on Gravitational Sources. Mod. Phys. Lett. 1995, A 10, 2801–2808. [Google Scholar]
- (a) Karolyhazy, F. Gravitation and Quantum Mechanics of Macroscopic Objects. Il Nuovo Cimento 1966, A 42, 390–402. [Google Scholar] [CrossRef] (b) Sasakura, N. An Uncertainty Relation of Space-Time. Prog. Theor. Phys. 1999, 102, 169–179. [Google Scholar]
- Ng, Y.J.; van Dam, H. Measuring the Foaminess of Spacetime with Gravity-Wave Interferometers. Found. Phys. 2000, 30, 795–805. [Google Scholar] [CrossRef]
- Ng, Y.J. From Computation to Black Holes and Space-time Foam. Phys. Rev. Lett. 2001, 86, 2946–2949, (erratum) 2002, 88, 139902. [Google Scholar] [CrossRef]
- Lloyd, S.; Ng, Y.J. Black Hole Computers. Sci. Am. 2005, 291, #5. 52–61. [Google Scholar] [CrossRef]
- (a) Christiansen, W.A.; Ng, Y.J.; van Dam, H. Probing Spacetime Foam with Extragalactic Sources. Phys. Rev. Lett. 2006, 96, 051301-1–051301-4, (erratum) 2007, 98, 259903. [Google Scholar] [CrossRef] (b) Christiansen, W.A.; Ng, Y.J.; van Dam, H. Reply to Diosi’s Comment on “Probing Spacetime Foam Sources”. Phys. Rev. Lett. 2007, 98, 259902. [Google Scholar]
- (a) Arzano, M.; Kephart, T.W.; Ng, Y.J. From Spacetime Foam to Holographic Foam Cosmology. Phys. Lett. 2007, B 649, 243–346. [Google Scholar] [CrossRef] (b) Maziashvili, M. Space-Time in Light of Karolyhazy Uncertainty Relation. Int. J. Mod. Phys. 2007, D 16, 1531–1539. [Google Scholar]
- Ng, Y.J. Holographic Foam, Dark Energy and Infinite Statistics. Phys. Lett. 2007, B 657, 10–14. [Google Scholar] [CrossRef]
- Requardt, M. About the Minimal Resolution of Space-Time Grains in Experimental Quantum Gravity. arXiv:0807.3619[gr-qc].
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum-Enhanced Measurements: Beating the Standard Quantum Limit. Science 2004, 306, 1330–1336. [Google Scholar] [CrossRef] [PubMed]
- Margolus, N.; Levitin, L.B. The Maximum Speed of Dynamical Evolution. Physica 1998, D 120, 188–195. [Google Scholar] [CrossRef]
- Note the qualification “average”. This result is not inconsistent with that found in Calmet, X.; Graesser, M.; Hsu, S.D. Minimum Length from Quantum Mechanics and Classical General Relativity. Phys. Rev. Lett. 2004, 93, 211101-1–211101-4. [Google Scholar] [CrossRef]
- (a) ’t Hooft, G. Salamfestschrift; Ali, A., et al., Eds.; World Scientific: Singapore, 1993; p. 284. [Google Scholar] (b) Susskind, L. The World as a Hologram. J. Math. Phys. (N.Y.). 1995, 36, 6377–6396. [Google Scholar] (c) Bekenstein, J.D. Black Holes and Entropy. Phys. Rev. 1973, D 7, 2333–2346. [Google Scholar] (d) Hawking, S. Particle Creation by Black Holes. Comm. Math. Phys. 1975, 43, 199–220. [Google Scholar] (e) Giddings, S.B. Black Holes and Massive Remnants. Phys. Rev. 1992, D 46, 1347–1352. [Google Scholar] (f) Bousso, R. The Holographic Principle. Rev. Mod. Phys. 2002, 74, 825–874. [Google Scholar]
- (a) Gambini, R.; Pullin, J. Holography in Spherically Symmetric Loop Quantum Gravity. arXiv:0708.0250[gr-qc]. (b) Husain, V. (unpublished).
- (a) Amelino-Camelia, G. Limits on the Measurability of Space-Time Distances in the Semi-Classical Approximation of Quantum Gravity. Mod. Phys. Lett. 1994, A 9, 3415–3422. [Google Scholar] (b) Amelino-Camlia, G. An Interferometric Gravitational Wave Detector as a Quantum-Gravity Apparatus. Nature 1999, 398, 216–218. [Google Scholar]
- For related effects of quantum fluctuations of spacetime geometry, see (a) Ford, L.H. Gravitons and Light Cone Fluctuations. Phys. Rev. 1995, D 51, 1692–1700. [Google Scholar] (b) Thompson, R.H.; Ford, L.H. Spectral line broadening and angular blurring due to spacetime geometry fluctuations. Phys. Rev. 2006, D 74, 024012-1–024012-12. [Google Scholar] (c) Hu, B.L.; Shiokawa, K. Wave propagation in stochastic spacetime: Localization, amplification, and particle creation. Phys. Rev. 1998, D 57, 3474–3483. [Google Scholar] (d) Hu, B.L.; Vergaguer, E. Stochastic Gravity: Theory and Applications. Living Rev. Rel. 2004, 7, 3. [Google Scholar]
- Ng, Y.J.; Christiansen, W.A.; van Dam, H. Probing Planck-scale Physics with Extragalacic Sources? Astrophys. J. 2003, 591, L87–L90. [Google Scholar] [CrossRef]
- Lieu, R.; Hillman, L.W. The Phase Coherenece of Light from Extragalactic Sources - Direct Evidence Against First Order Planck Scale Fluctuations in Time and Space. Astrophys. J. 2003, 585, L77–L80. [Google Scholar] [CrossRef]
- Perlman, E.S.; et al. The Apparent Host Galaxy of PKS 1413+135: HST, ASCA and VLBA Observations. Astro. J. 2002, 124, 2401–2412. [Google Scholar] [CrossRef]
- Lloyd, S. Computational Capacity of the Universe. Phys. Rev. Lett. 2002, 88, 237901-1–237901-4. [Google Scholar] [CrossRef]
- Krauss, L.M.; Turner, M.S. Geometry and Destiny. Gen. Rel. Grav. 1999, 31, 1453–1459. [Google Scholar] [CrossRef]
- (a) Perlmutter, S.; et al. Measurements of Omega and Lambda from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] (b) Riess, A.G.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] (c) Bennett, C.L.; et al. First Year Wilkenson Microwave Anisotropy Probe (WMAP) Observations: Preliminary Maps and Basic Results. Astrophys. J. Suppl. 2003, 148, 1. [Google Scholar] (d) Allen, S.W.; et al. Cosmological Constraints from the Local X-Ray Luminosity Function of the Most X-Ray Luminous Galaxy Clusters. Mon. Not. Roy. Astron. Soc. 2003, 342, 287–29. [Google Scholar]
- (a) Doplicher, S.; Haag, R.; Roberts, J. Local Observables and Particle Statistics I. Commun. Math. Phys. 1971, 23, 199–230. [Google Scholar] (b) Doplicher, S.; Haag, R.; Roberts, J. Local Observables and Particle Statistics II. Commun. Math. Phys. 1974, 35, 49–85. [Google Scholar]
- Govorkov, A.B. Parastatistics and Parafields. Theor. Math. Phys. 1983, 54, 234–241. [Google Scholar] [CrossRef]
- Greenberg, O.W. Example of Infinite Statistics. Phys. Rev. Lett. 1990, 64, 705–708. [Google Scholar] [CrossRef] [PubMed]
- Fredenhagen, K. On the Existence of Antiparticles. Commun. Math. Phys. 1981, 79, 141–151. [Google Scholar] [CrossRef]
- For work on nonlocality in theories using Hopf algebra or Moyal-plane, see (a) Arzano, M. Quantum Fields, Non-Locality and Quantum Group Symmetries. arXiv:0710.1083 [hep-th]. (b) Balachandran, A.P.; et al. S-Matrix on the Moyal Plane: Locality versus Lorentz Invariance. arXiv:0708.1379 [hep-th].
- (a) Jejjala, V.; Kavic, M.; Minic, D. Fine Structure of Dark Energy and New Physics. arXiv:0705.4581 [hep-th]. (b) Benatti, F.; Floreanini, R. Non-Standard Neutral Kaons Dynamics from D-Brane Statistics. Annals Phys. 1999, 273, 58–71. [Google Scholar] (c) Medved, A.J.M. A comment or two on holographic dark energy. arXiv:0802.1753 [hep-th].
- (a) Strominger, A. Black Hole Statistics. Phys. Rev. Lett. 1993, 71, 3397–3400. [Google Scholar] (b) Volovich, I.V. D-branes, Black Holes and SU (∞) Gauge Theory. arXiv:hep-th/9608137 and references therein.
- Giddings, S.B. Black Holes, Information, and Locality. arXiv:0705.2197 [hep-th].
- Horowitz, G.T. Black Holes, Entropies, and Information. arXiv:0708.3680 [astro-ph].
- Ahluwalia, D.V. Quantum Measurements, Gravitation, and Locality. Phys. Lett. 1994, B 339, 301–303. [Google Scholar] [CrossRef]
- (a) Chen, W.; Wu, Y.S. Implications of a Cosmological Constant Varying as R−2. Phys. Rev. 1990, D 41, 695–698. [Google Scholar] (b) Sorkin, R.D. Forks in the Road, on the Way to Quantum Gravity. Int. J. Theor. Phys 1997, 36, 2759–2781. [Google Scholar] (c) Ng, Y.J.; van Dam, H. A Small but Nonzero Cosmological Constant. Int. J. Mod. Phys. 2001, D 10, 49–55. [Google Scholar]
- van der Bij, J.J.; van Dam, H.; Ng, Y.J. The Exchange of Massless Spin-Two Particles. Physica 1982, A116, 307–320. [Google Scholar] [CrossRef]
- (a) Zimdahl, W.; Pavon, D. Interacting Holographic Dark Energy. arXiv:0606555 [astro-ph]. (b) Biswas, T.; et al. Current Acceleration from Dilaton and Stringy Cold Dark Matter. Phys. Rev. 2006, D 74, 063501-1–063501-13. [Google Scholar] (c) Zimdahl, W. Dark Energy: A Unifying View. arXiv:0705.2131 [gr-qc]. (d) Abdalla, E.; et al. Signature of the interaction between dark energy and dark matter in galaxy clusters. arXiv:0710.1198 [astro-ph]. (e) Pavon, D.; Wang, B. Le Chatelier-Braun principle in cosmological physics. arXiv:0712.0565 [gr-qc].
- For more discussions on holographic cosmology, see, e.g., (a) Fischler, W.; Susskind, L. Holography and Cosmology. arXiv:hep-th/9806039. (b) Easther, R.; Lowe, D. Holography, Cosmology, and the Second Law of Thermodynamics. Phys. Rev. Lett. 1999, 82, 4967–4970. [Google Scholar] (c) Veneziano, G. Prebangian Origin of our Entropy and Time Arrow. Phys. Lett. 1999, B 454, 22–26. [Google Scholar] (d) Kaloper, N.; Linde, A. Cosmology versus Holography. Phys. Rev. 1999, D 60, 103509-1–103509-7. [Google Scholar] (e) Cohen, A.G.; et al. Effective Field Theory, Black Holes, and the Cosmological Constant. Phys. Rev. Lett. 1999, 82, 4971–4974. [Google Scholar] (f) Horava, P.; Minic, D. Probable Values of the Cosmological Constant in a Holographic Theory. Phys. Rev. Lett. 2000, 85, 1610–1613. [Google Scholar] (g) Thomas, S. Holography Stabilizes the Vacuum Energy. Phys. Rev. Lett. 2002, 89, 081301-1–081301-4. [Google Scholar] (h) Hsu, S.D.H. Entropy Bounds and Dark Energy. Phys. Lett. 2004, B 594, 13–16. [Google Scholar] (i) Li, M. A Model of Dark Energy. Phys. Lett. 2004, B 603, 1–5. [Google Scholar] (j) Lee, J.-W.; Lee, J.; Kim, H.-C. Dark energy from vacuum entanglement. arXiv:hep-th/0701199. (k) Cai, R.-G. A dark energy model characterized by the age of the Universe. arXiv:0707.4049 [hep-th]. (l) Horvat, R. Holographic dark energy: quantum correlations against thermodynamical description. arXiv:0711.4013 [gr-qc]. (m) Padmanabhan, T. Emergent Gravity and Dark Energy. arXiv:0802.1798 [gr-qc]. (n) Ma, Y.Z.; Gong, Y.; Chen, X. Features of holographic dark energy under the combined cosmological constraints. arXiv:0711.1641 [astro-ph].
- For a related view on holography, information theory and inflationary universe, see (a) Zizzi, P.A. Quantum Foam and de Sitter-like Universe. Int. J. Theor. Phys. 1999, 38, 2333–2348. [Google Scholar] (b) Zizzi, P.A. Holography, Quantum Geometry, and Quantum Information Theory. Entropy 2000, 2, 39–69. [Google Scholar]
- Salecker, H.; Wigner, E.P. Quantum Limitations of the Measurement of Space-Time Distances. Phys. Rev. 1958, 109, 571–577. [Google Scholar] [CrossRef]
- Barrow, J.D. Wigner Inequalities for a Black Hole. Phys. Rev. 1996, D54, 6563–6564. [Google Scholar] [CrossRef]
- Gambini, R.; Porto, R.; Pullin, J. Fundamental Decoherence from Quantum Gravity: A Pedagogical Review. Gen. Rel. Grav. 2007, 39, 1143–1156. [Google Scholar] [CrossRef]
- Some of the viewpoints on this matter can be found in, e.g., (a) Susskind, L.; Lindesay, J. An Introduction to Black Holes, Information and the String Theory Revolution: The Holographic Universe; World Scientific Publishing: Singapore, 2005. [Google Scholar] (b) Ashtekar, A.; Baez, J.C.; Corichi, A.; Krasnov, K. Quantum geometry and black hole entropy. Phys. Rev. Lett. 1998, 80, 904–907. [Google Scholar] (c) Frampton, P.H.; Hsu, S.D.H.; Reeb, D.; Kephart, T.W. What is the entropy of the Universe? arXiv:0801.1847 [hep-th].
- Ng, Y.J. Proceedings of the Fortieth Karpacz Winter School on Theoretical Physics; Kowalski-Glikman, J., Amelino-Camelia, G., Eds.; Springer: Berlin, 2005; p. 321.
- (a) Amelino-Camelia, G.; Ellis, J.; Mavromatos, N.E.; Nanopoulos, D.V. Distance Measurement and Wave Dispersion in a Liouville String Approach to Quantum Gravity. Int. J. Mod. Phys. 1997, A12, 607–623. [Google Scholar] (b) Amelino-Camelia, G.; Ellis, J.; Mavromatos, N.E.; Nanopoulos, D.V.; Sarkar, S. Tests of Quantum Gravity from Observations of γ-Ray Bursts. Nature 1998, 393, 763–765. [Google Scholar]
- (a) Aloisio, R.; et al. A Fluctuating Energy-Momentum May Produce an Unstable World. Astropart. Phys. 2003, 20, 369–376. [Google Scholar] (b) Le Gallou, R. New Constraints on Space-Time Planck Scale Fluctuations from Established High Energy Astronomy Observations. Astropart. Phys. 2004, 20, 703–708. [Google Scholar]
- Albert, J.; et al. [MAGIC collaboration] Variable VHE Gamma-Ray Emission from Markarian 501. Astrophys. J. 2007, 669, 862–883. [Google Scholar] [CrossRef]
- Albert, J.; et al. Probing Quantum Gravity Using Photons from a Mkn 501 Flare Observed by MAGIC. arXiv:0708.2889 [astro-ph].
- The Pierre Auger collaboration. Correlation of the Highest-Energy Cosmic Rays with Nearby Extragalactic Objects. Science 2007, 318, 938–943. [Google Scholar] [Green Version]
© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ng, Y.J. Spacetime Foam: From Entropy and Holography to Infinite Statistics and Nonlocality. Entropy 2008, 10, 441-461. https://doi.org/10.3390/e10040441
Ng YJ. Spacetime Foam: From Entropy and Holography to Infinite Statistics and Nonlocality. Entropy. 2008; 10(4):441-461. https://doi.org/10.3390/e10040441
Chicago/Turabian StyleNg, Y. Jack. 2008. "Spacetime Foam: From Entropy and Holography to Infinite Statistics and Nonlocality" Entropy 10, no. 4: 441-461. https://doi.org/10.3390/e10040441





