Entropy, Closures and Subgrid Modeling
Abstract
:1. Introduction
2. Barotropic vorticity equation
3. Statistical Mechanical Equilibrium (SME) States
3.1. Standard beta-plane
4. Statistical closure equations for homogeneous turbulence
4.1. The homogeneous DIA closure equations

4.2. Homogeneous SCFT and LET closure theories
5. Vorticity equation and DIA closure on the sphere
6. EDQNM closure on the sphere
7. Adiabatic invariants, zonalization and vortex condensation.
8. Subgrid-scale parameterizations
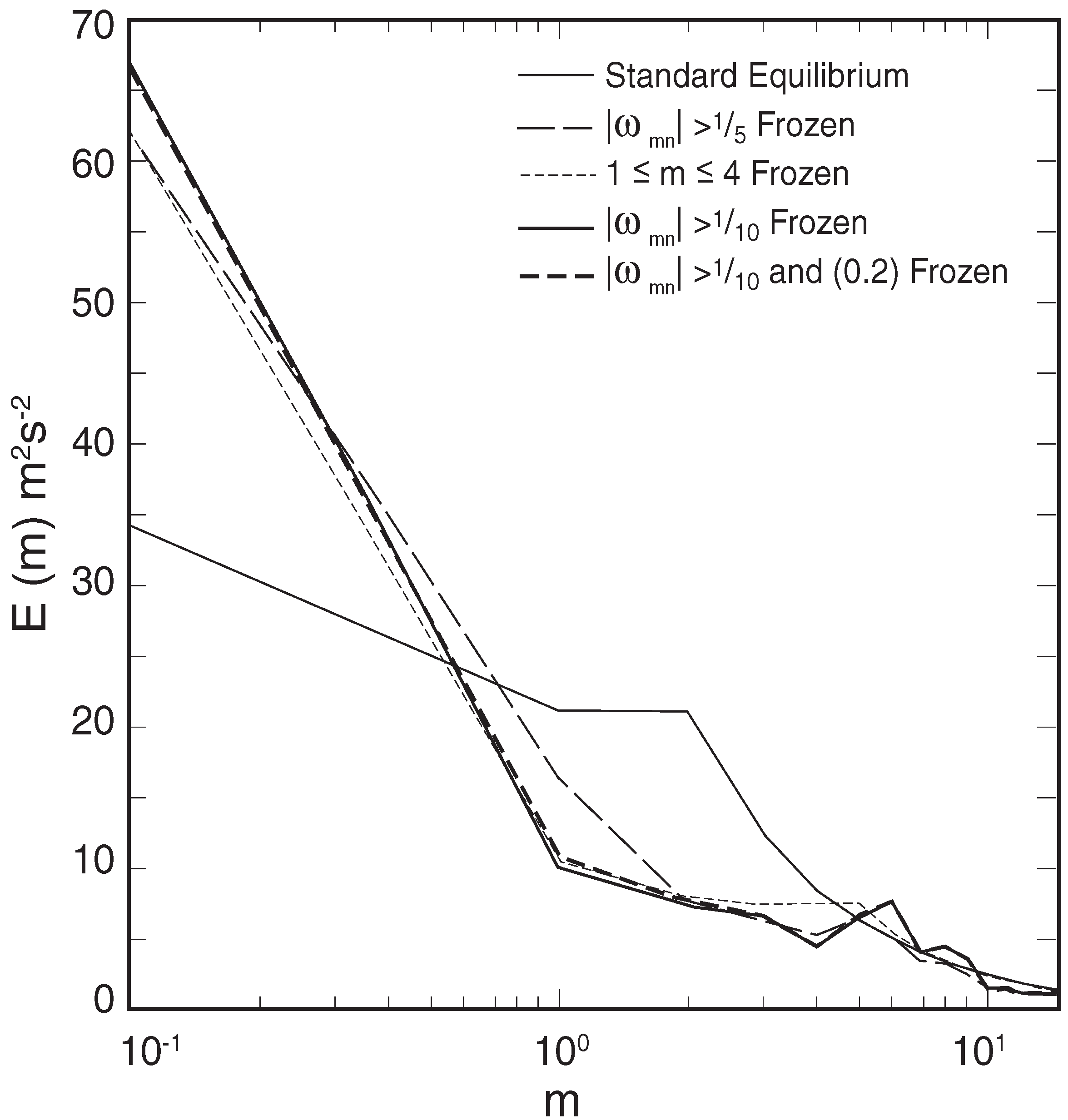
8.1. The EDQNM Closure
8.2. The DIA closure
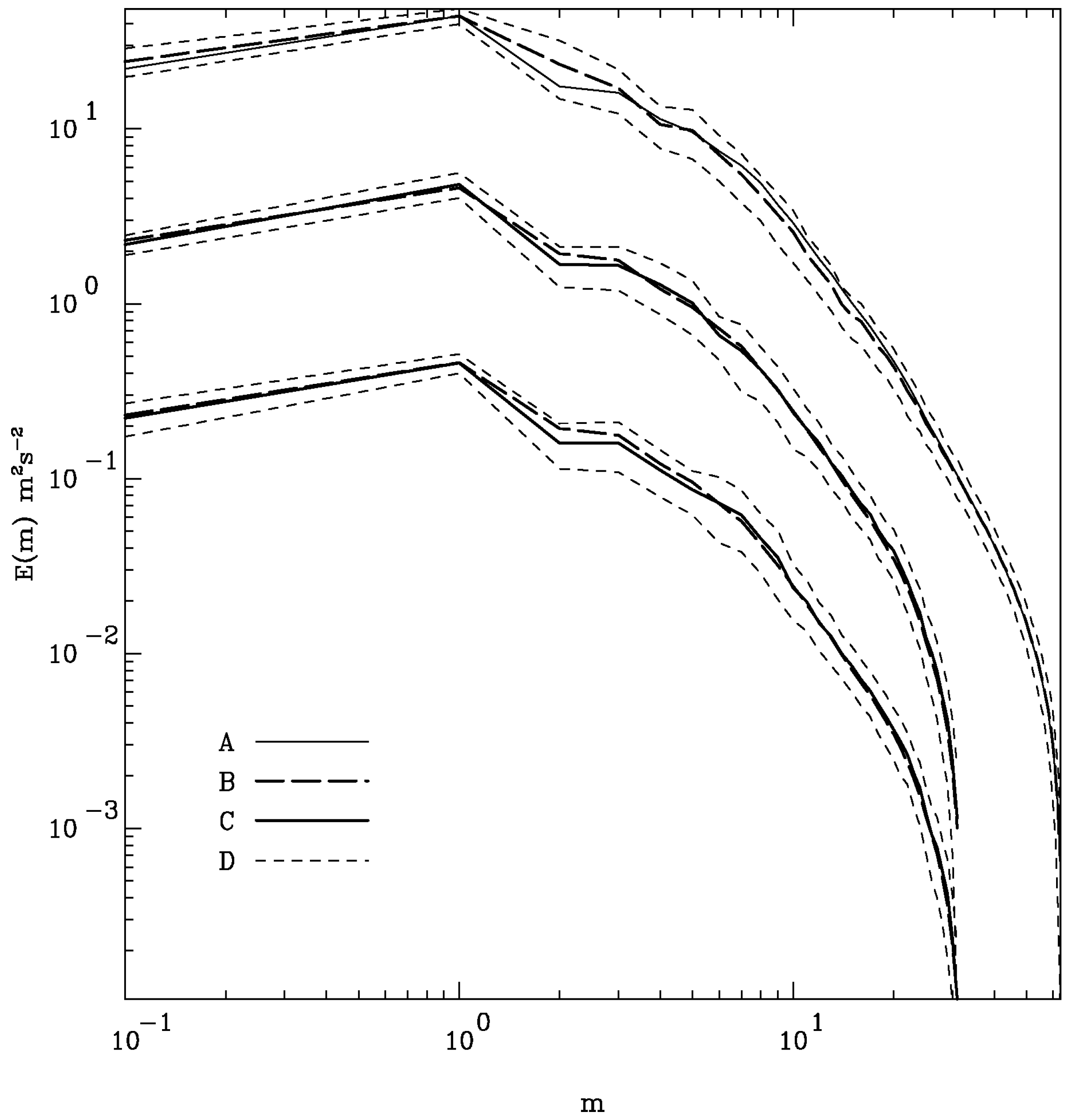
9. Comparisons of DNS and LES with subgrid-scale parameterizations
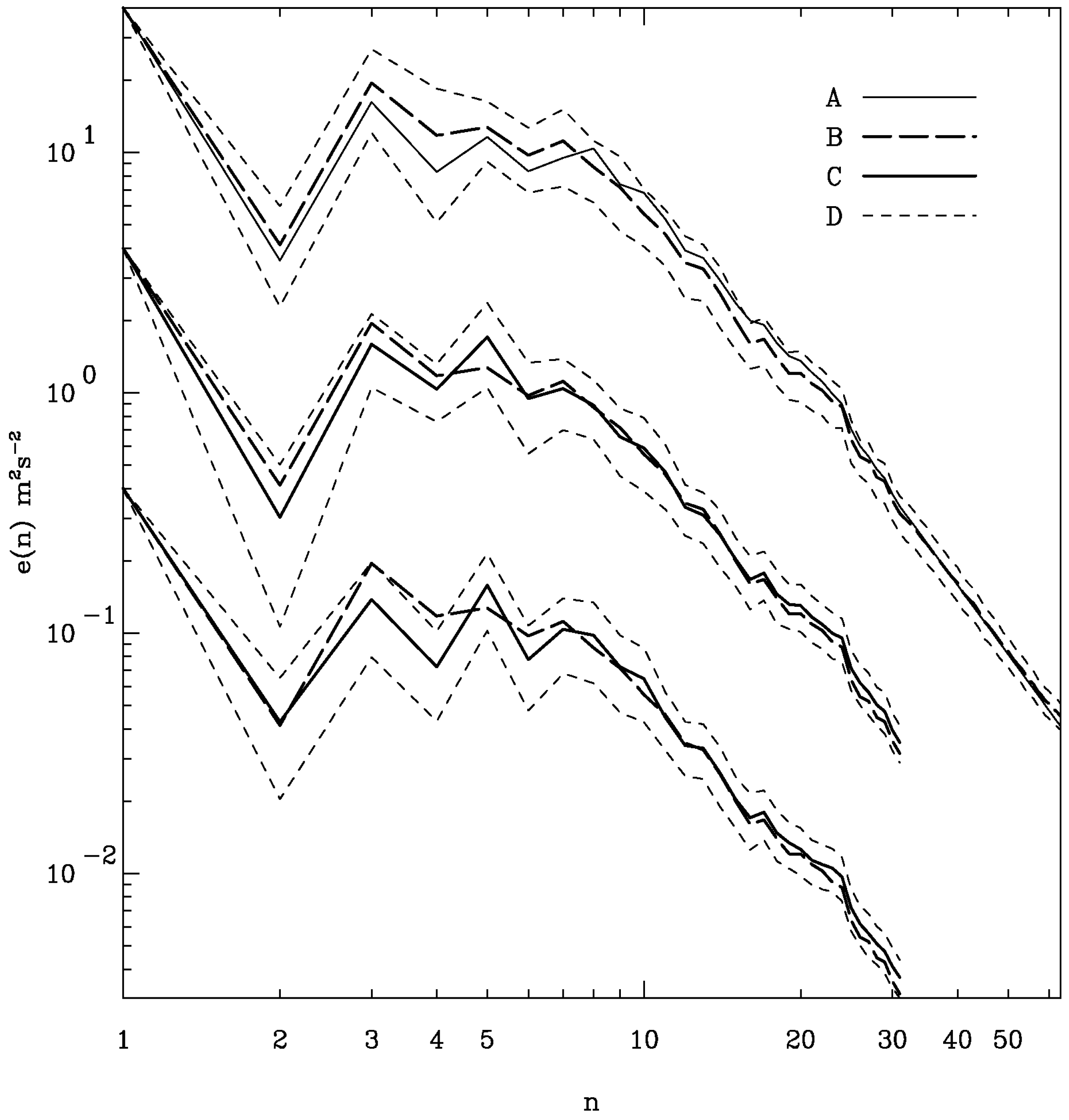
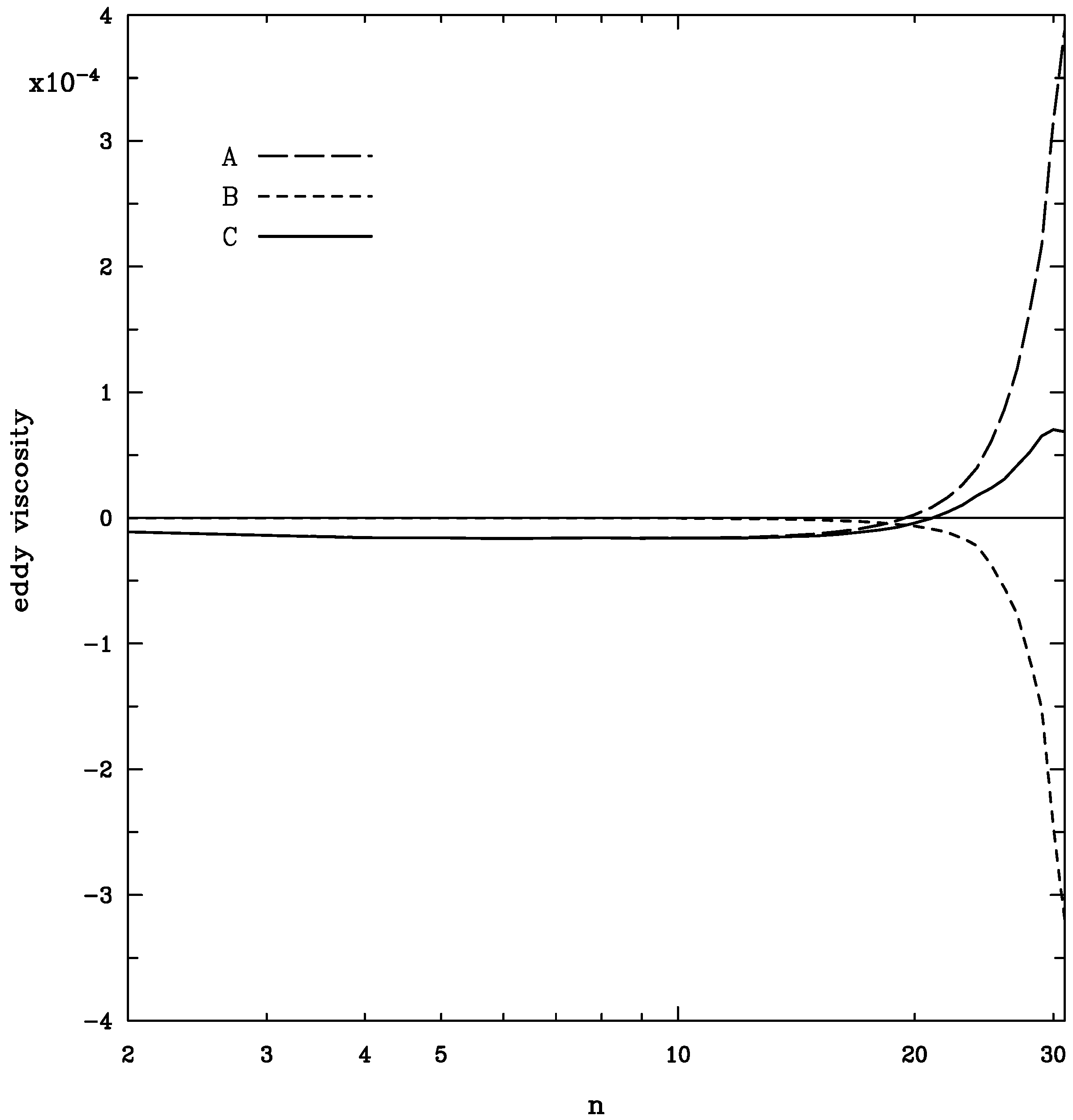
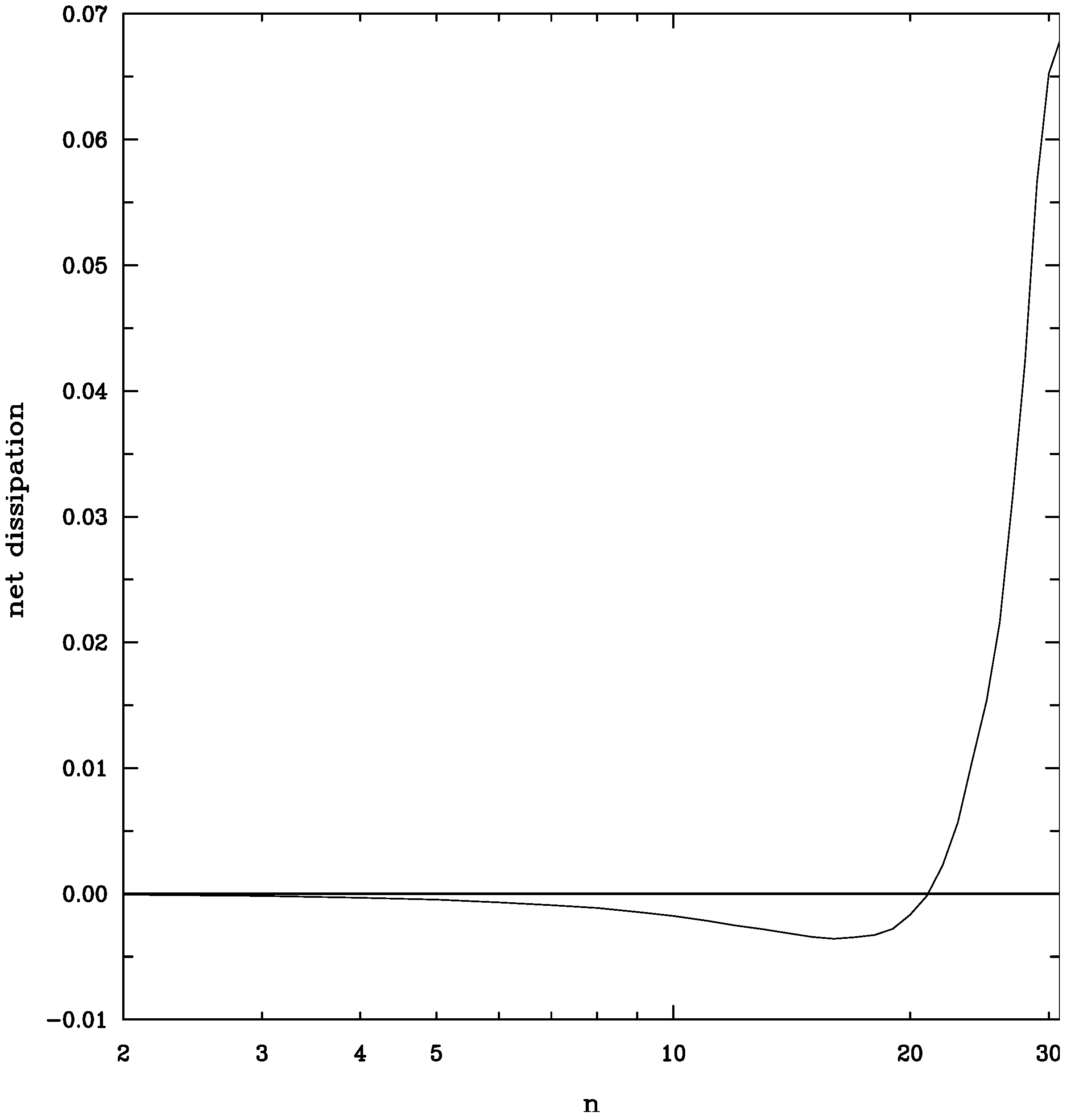
10. Closures and subgrid-scale terms for inhomogeneous geophysical flows
10.1. QDIA closure equations
10.2. Generalized Langevin Equation
10.3. Subgrid terms
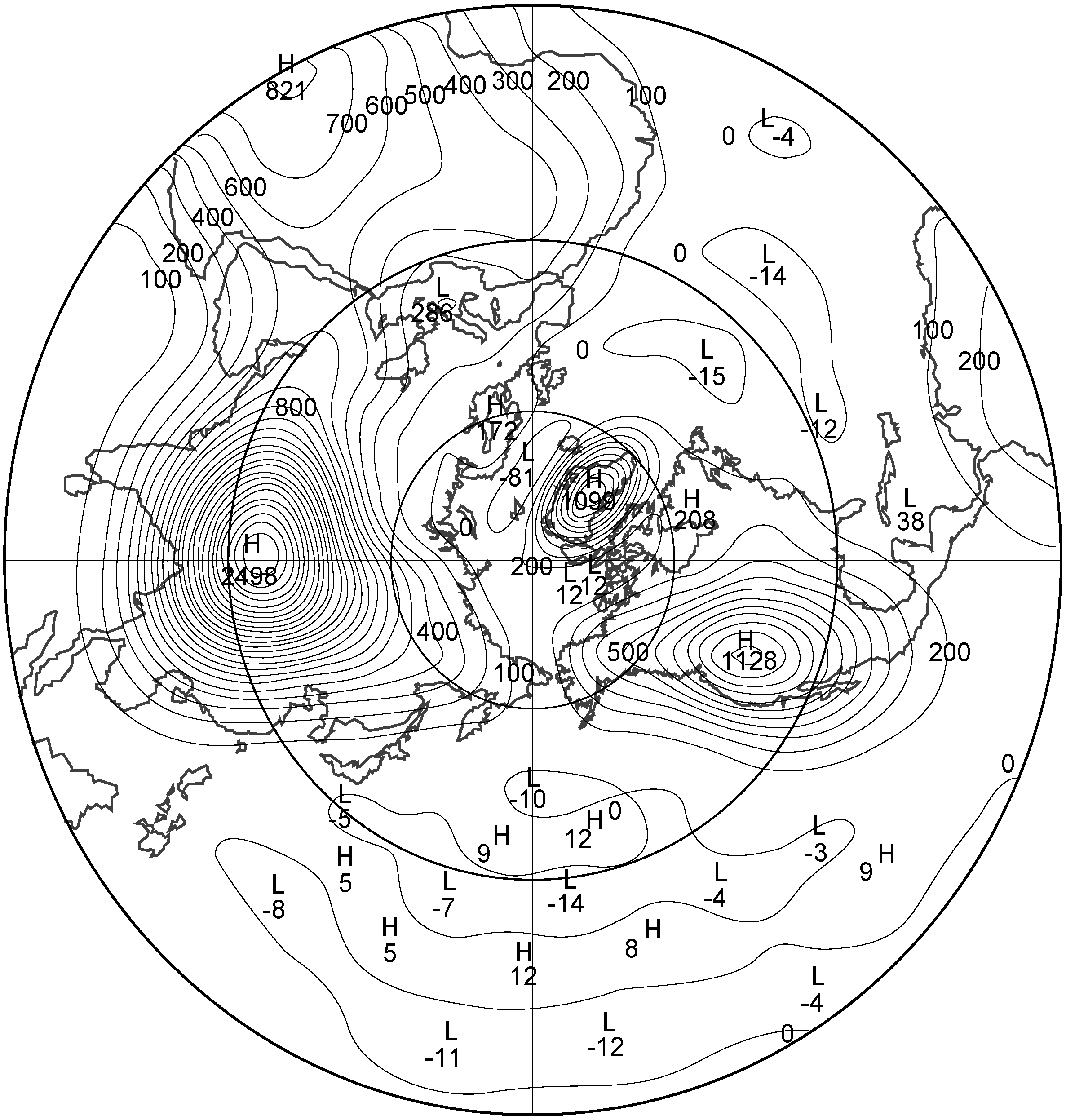
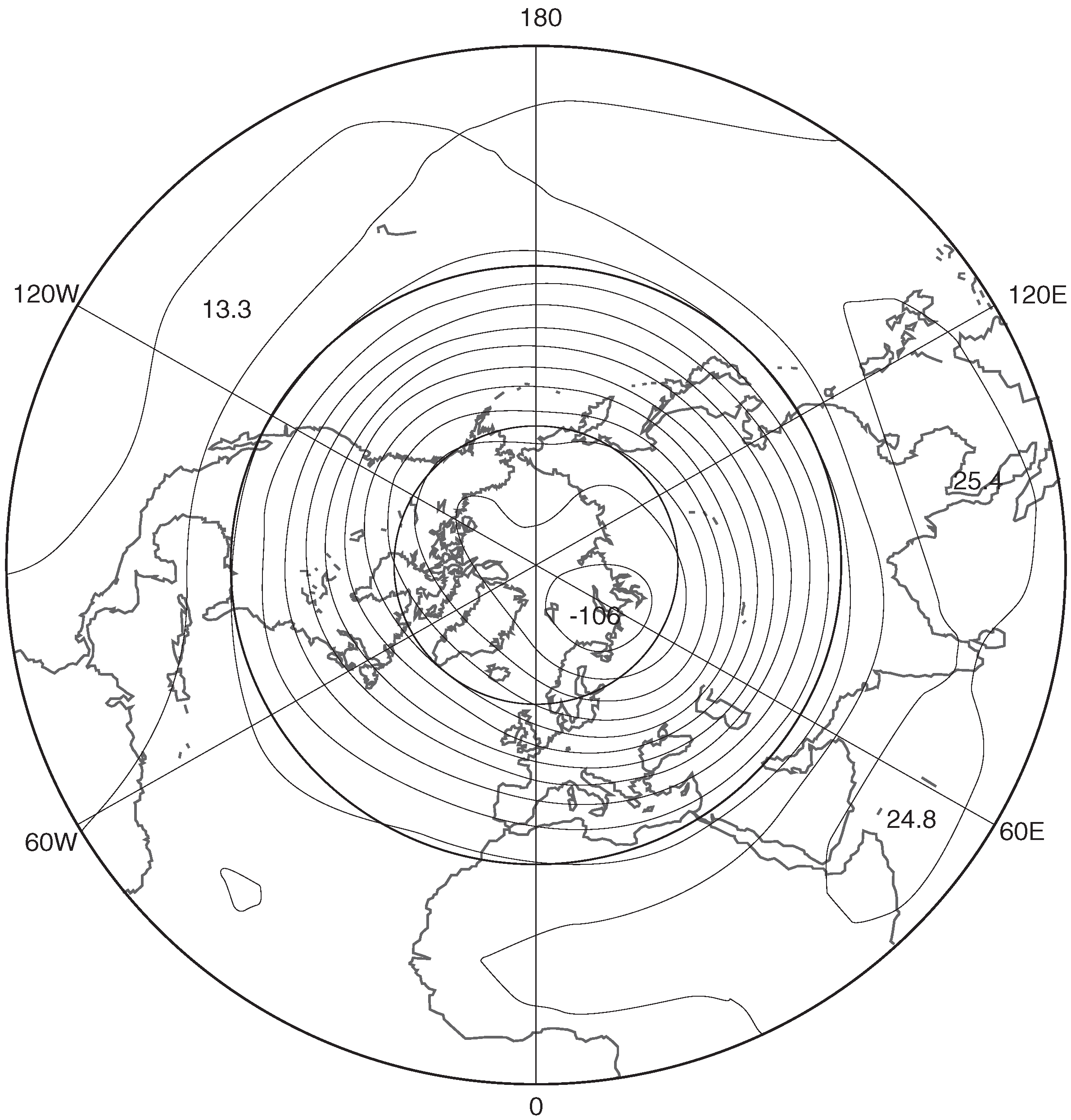
11. QDIA closure based SSP’s for global atmospheric flow
11.1. Canonical equilibrium

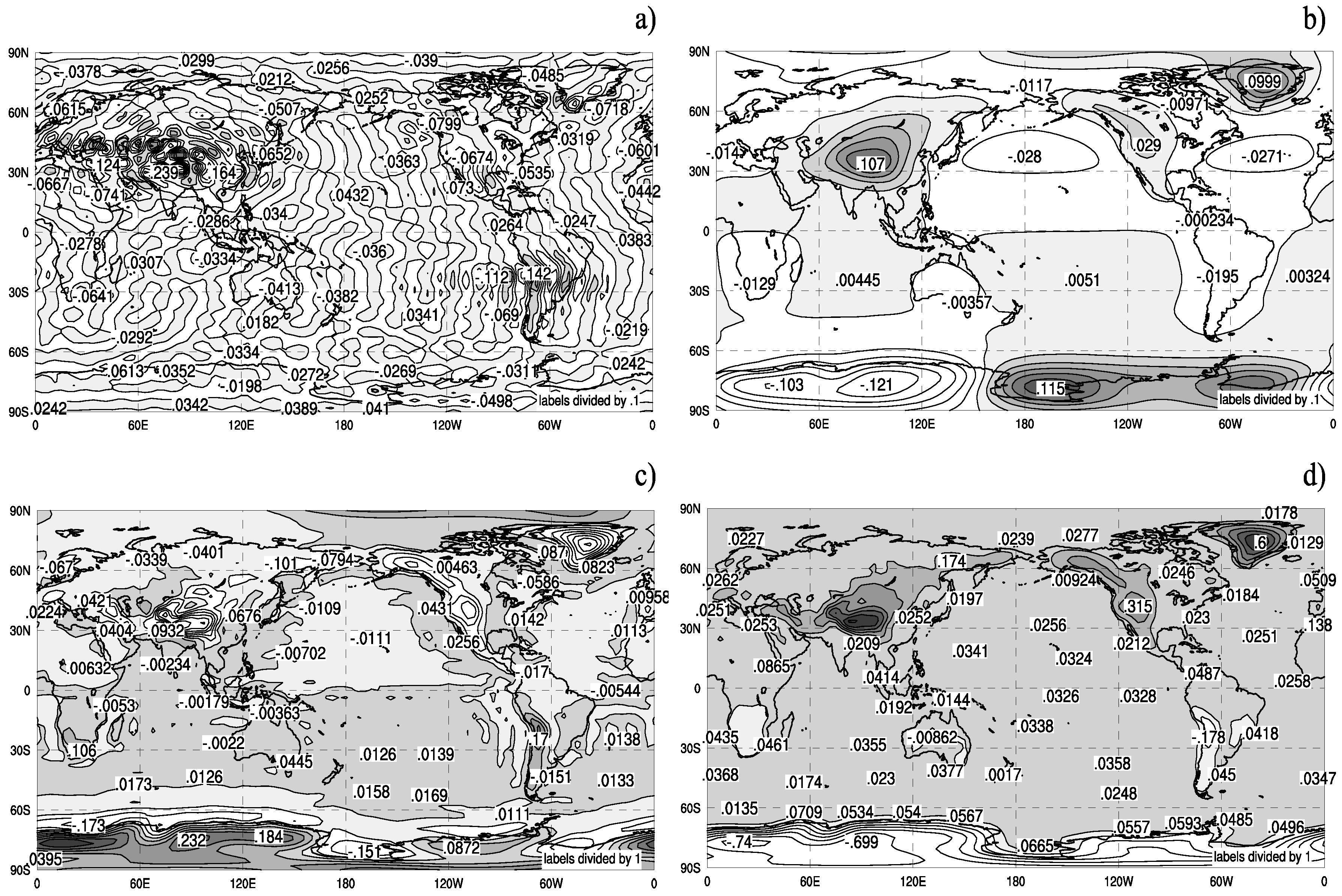
11.2. Nonequilibrium results

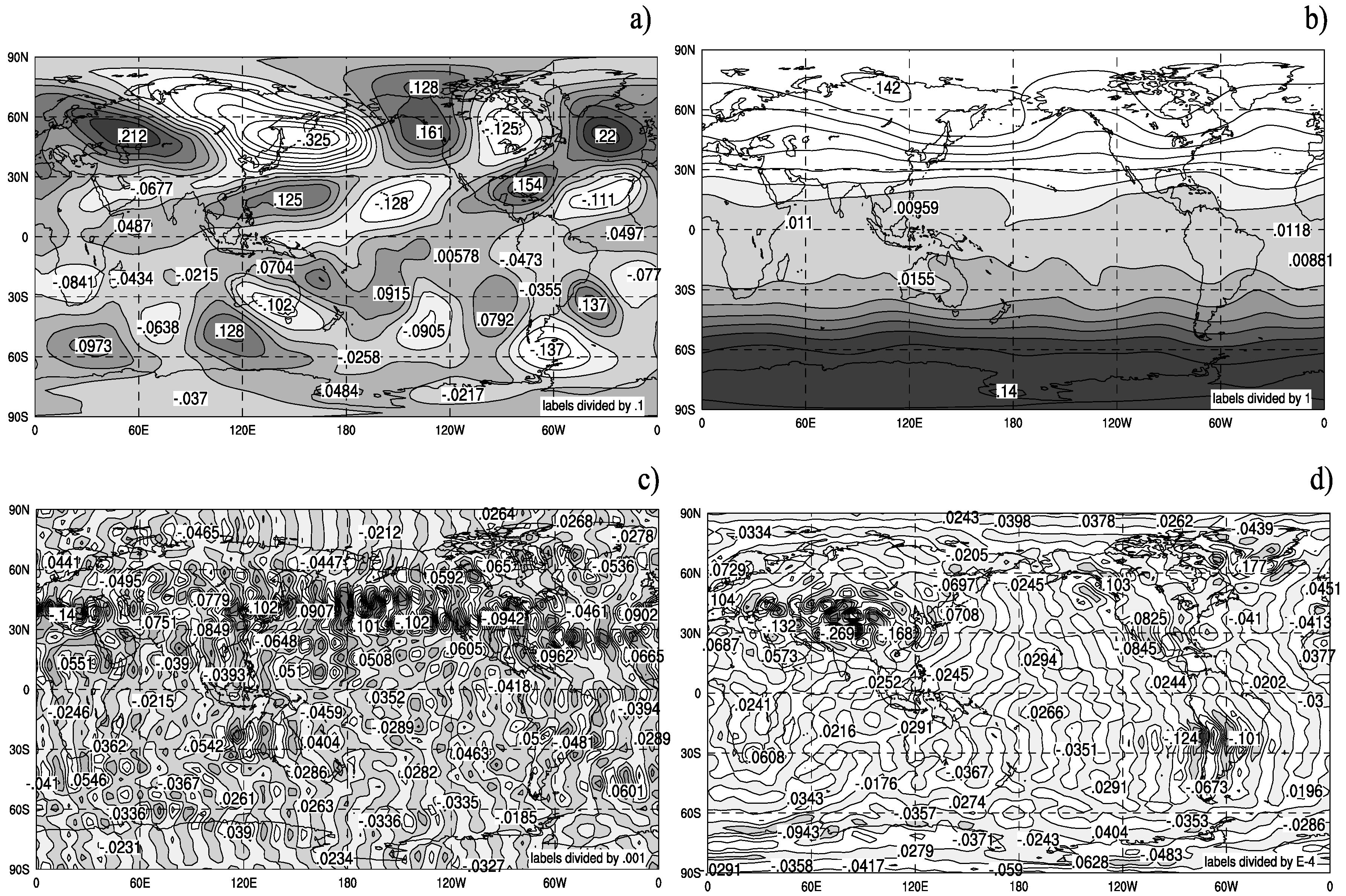
11.3. Comparison with subgrid terms obtained from entropy methods
12. Summary
References and Notes
- Kraichnan, R. H. Inertial ranges in two-dimensional turbulence. Phys. Fluids 1967, 10, 1417. [Google Scholar] [CrossRef]
- Kolmogorov, A. The local structure of turbulence in incompressible viscous fluid for very large Reynolds number. Dokl. Akad. Nauk SSSR 1941, 30, 301. [Google Scholar] [CrossRef]
- Nastrom, G.; Gage, K. A climatology of atmospheric wavenumber spectra of wind and temperature observed by commercial aircraft. J. Atmos. Sci. 1985, 42, 950. [Google Scholar] [CrossRef]
- Frederiksen, J. Instability theory and predictability of atmospheric disturbances., volume Frontiers in Turbulence and Coherent Structures of World Scientific Lecture Notes in Complex Systems. World Scientific Press, 2007. [Google Scholar]
- Onsager, L. Statistical hydrodynamics. Nouvo Cimento 1949, 6, 279. [Google Scholar] [CrossRef]
- Kraichnan, R.; Montgomery, D. Two-dimensional turbulence. Rep. Prog. Phys. 1980, 43, 547. [Google Scholar] [CrossRef]
- Kraichnan, R. Statistical dynamics of two-dimensional flow. J. Fluid Mech. 1975, 67, 155. [Google Scholar] [CrossRef]
- Frederiksen, J.; Sawford, B. Statistical dynamics of two-dimensional inviscid flow on a sphere. J. Atmos Sci. 1980, 37, 717. [Google Scholar] [CrossRef]
- Salmon, R.; Holloway, G.; Hendershott, M. The equilibrium statistical mechanics of simple quasi-geostrophic models. J. Fluid Mech. 1976, 75, 691. [Google Scholar] [CrossRef]
- Frederiksen, J.; Sawford, B. Topographic waves in nonlinear and linear spherical barotropic models. J. Atmos. Sci. 1981, 38, 69. [Google Scholar] [CrossRef]
- Sawford, B.; Frederiksen, J. Mountain torque and angular momentum in barotropic planetary flows: Equilibrium solutions. Q. J. R. Meteorol. Soc. 1983, 109, 309. [Google Scholar] [CrossRef]
- Bretherton, F.; Haidvogel, D. Two-dimensional turbulence above topography. J. Fluid Mech. 1976, 78, 129. [Google Scholar] [CrossRef]
- Arnold, V. On conditions for nonlinear stability of plane stationary curvilinear flows of an ideal fluid. Sov. Math. Dokl. 1965, 6, 773. [Google Scholar]
- Frederiksen, J. Eastward and westward flows over topography in nonlinear and linear barotropic models. J. Atmos. Sci. 1982, 39, 2477. [Google Scholar] [CrossRef]
- Frederiksen, J.; Carnevale, G. Stability properties of exact nonzonal solutions for flow over topography. Geophys. Astrophys. Fluid Dyn. 1986, 35, 173. [Google Scholar]
- Carnevale, G.; Frederiksen, J. Nonlinear stability and statistical mechanics of flow over topography. J. Fluid Mech. 1987, 175, 157. [Google Scholar] [CrossRef]
- Miller, J. Statistical mechanics of Euler equations in two dimensions. Phys. Fluids A 1990, 65, 2137. [Google Scholar] [CrossRef] [PubMed]
- Miller, J.; Weichman, P.; Cross, M. Statistical mechanical mechanics, Euler equation, and Jupiter’s red spot. Phys. Rev. A 1992, 45, 2328. [Google Scholar] [CrossRef] [PubMed]
- Robert, R. A maximum entropy principle for two-dimensional Euler equations. J. Stat. Phys. 1991, 65, 531. [Google Scholar] [CrossRef]
- Sommeria, J.; Nore, C.; Dumont, T.; Robert, R. Theorie statistique de la tache rouge de Jupiter. C. R. Acad. Sci. Paris 1991, 312, 999. [Google Scholar]
- Turkington, B.; Majda, A.; Haven, K.; DiBattista, M. Statistical equilibrium predictions of jets and spots on Jupiter. Proc. Natl. Acad. Sci. 2001, 98, 12346. [Google Scholar] [CrossRef] [PubMed]
- Isichenko, M.; Gruzinov, A. Coherent structures, and Gaussian turbulence in 2-dimensional (2d) magnetohydrodynamics (mhd). Phys. Plasmas 1994, 1, 1802. [Google Scholar] [CrossRef]
- Majda, A.; Holen, M. Dissipation, topography, and statistical theories for large-scale coherent structure. Comm. Pure Appl. Math. 1998, 50, 1183. [Google Scholar] [CrossRef]
- Ellis, R.; Haven, K.; Turkington, B. Nonequivalent statistical equilibrium ensembles and refined stability theorems for most probable flows. Nonlinearity 2002, 15, 239. [Google Scholar] [CrossRef]
- Abramov, R.; Majda, A. Statsitically relevant conserved quantities for truncated quasi-geostrophic flow. Proc. Natl. Acad. Sci. 2003, 100, 3841. [Google Scholar] [CrossRef] [PubMed]
- Frederiksen, J. Nonlinear stability of baroclinic flows over topography. Geophys. Astrophys. Fluid Mech. 1991, 57, 85. [Google Scholar] [CrossRef]
- Frederiksen, J. Nonlinear studies on the effect of topography on baroclinic zonal flows. Geophys. Astrophys. Fluid Dyn. 1991, 59, 57. [Google Scholar] [CrossRef]
- Frederiksen, J.; Dix, M.; Kepert, S. Systematic energy errors and the tendency toward canonical equilibrium in atmospheric general circulation models. J. Atmos. Sci. 1996, 53, 887. [Google Scholar] [CrossRef]
- Treguier, A. Topographically generated steady currents in barotropic turbulence. Geophys. Astrophys. Fluid Dyn. 1989, 47, 43. [Google Scholar] [CrossRef]
- Treguier, A.; McWilliams, J. Topographic influences on wind-driven, stratified flow in a beta-plane channel: An idealized model for the Antarctic circumpolar current. J. Phys. Oceanogr. 1990, 20, 321. [Google Scholar] [CrossRef]
- Griffa, A.; Salmon, R. Wind-driven ocean circulation and equilibrium statistical mechanics. J. Mar. Res. 1989, 47, 457. [Google Scholar] [CrossRef]
- Cummins, P. Inertial gyres in decaying and forced geostrophic turbulence. J. Mar. Res. 1992, 50, 545. [Google Scholar] [CrossRef]
- Wang, J.; Vallis, G. Emergence of Fofonoff states in inviscid and viscous ocean circulation models. J. Mar. Res. 1994, 52, 83. [Google Scholar] [CrossRef]
- Zou, J.; Holloway, G. Entropy maximization tendency in topographic turbulence. J. Fluid Mech. 1994, 263, 361. [Google Scholar] [CrossRef]
- Nost, O.; Nilsson, J.; Nycander, J. On the asymmetry between cyclonic and anticyclonic flow in basins with slipping boundaries. J. Phys. Oceanogr. 2008, 38, 771. [Google Scholar] [CrossRef]
- Holloway, G. Eddies, waves, circulation, and mixing: Statistical geofluid mechanics. Annal. Rev. Fluid Mech. 1986, 18, 91. [Google Scholar] [CrossRef]
- Majda, A.; Wang, X. Nonlinear dynamics and statistical theories for basic geophysical flows, Cambridge University Press: Cambridge, 2006.
- Dubinkina, S.; Frank, J. Statistical mechanics of Arakawa’s discretizations. J. Comp. Phys. 2007, 227, 1286. [Google Scholar] [CrossRef]
- Timofeyev, I. Systematic deviations from Gaussianity in models of quasigeostrophic turbulence. Phys.Fluids 2007, 19, 116603. [Google Scholar] [CrossRef]
- Kurgansky, M. The energy spectrum in a barotropic atmosphere. Adv. Geosci. 2008, 15, 17. [Google Scholar] [CrossRef]
- Kraichnan, R. Irreversible statistical mechanics of incompressible hydrodynamic turbulence. Phys. Rev. 1958, 109, 1407. [Google Scholar] [CrossRef]
- Kraichnan, R. H. The structure of isotropic turbulence at very high Reynolds number. J. Fluid. Mech. 1959, 5, 497. [Google Scholar] [CrossRef]
- Herring, J. Self-consistent-field approach to turbulence theory. Phys. Fluids 1965, 8, 2219. [Google Scholar] [CrossRef]
- Herring, J. Self-consistent-field approach to nonstationary turbulence. Phys. Fluids 1966, 9, 2106. [Google Scholar] [CrossRef]
- McComb, W. A local energy-transfer theory of isotropic turbulence. J. Phys. A 1974, 7, 632. [Google Scholar] [CrossRef]
- McComb, W.; Filipiak, M.; Shanmugasundaram, V. Rederivation and further assessment of the LET theory of isotropic turbulence, as applied to passive scalar convection. J. Fluid Mech. 1992, 245, 279. [Google Scholar] [CrossRef]
- McComb, W.; Quinn, A. Two-point two-time closures applied to forced isotropic turbulence. Physica A 2003, 317, 487. [Google Scholar] [CrossRef]
- Kraichnan, R. Classical fluctuation-relaxation theorem. Phys. Rev. 1959, 113, 1181. [Google Scholar] [CrossRef]
- Leith, C. Climate response and fluctuation dissipation. J. Atmos. Sci. 1975, 32, 2022. [Google Scholar] [CrossRef]
- Deker, U.; Haake, F. Fluctuation-dissipation theorems for classical processes. Phys. Rev. A 1975, 6, 2043–2056. [Google Scholar] [CrossRef]
- Carnevale, G.; Frederiksen, J. Viscosity renormalization based on direct-interaction closure. J. Fluid Mech. 1983, 131, 289. [Google Scholar] [CrossRef]
- Frederiksen, J.; Davies, A.; Bell, R. Closure theories with non-Gaussian restarts for truncated two-dimensional turbulence. Phys. Fluids 1994, 6, 3153. [Google Scholar] [CrossRef]
- Kiyani, K.; McComb, W. Time-ordered fluctuation-dissipation relation for incompressible isotropic turbulence. Phys. Rev. E 2004, 70, 066303. [Google Scholar] [CrossRef] [PubMed]
- Orszag, S. Analytical theories of turbulence. J. Fluid Mech. 1970, 41, 363. [Google Scholar] [CrossRef]
- Leith, C. Atmospheric predictability and two-dimensional turbulence. J. Atmos. Sci. 1971, 28, 145. [Google Scholar] [CrossRef]
- Bowman, J.; Krommes, J.; Ottaviani, M. The realizable Markovian closure I. General theory, with applications to 3-wave dynamics. Phys. Fluids 1993, 5, 3558. [Google Scholar] [CrossRef]
- Frederiksen, J.; Davies, A. Eddy viscosity and stochastic backscatter parameterizations on the sphere for atmospheric circulation models. J. Atmos. Sci. 1997, 54, 2475. [Google Scholar] [CrossRef]
- Kraichnan, R. An almost Markovian Galilean invariant turbulence model. J. Fluid Mech. 1971, 47, 513. [Google Scholar] [CrossRef]
- Kraichnan, R. Inertial-range transfer in two and three dimensional turbulence. J. Fluid Mech. 1971, 47, 525. [Google Scholar] [CrossRef]
- Leith, C.; Kraichnan, R. Predictability of turbulent flows. J. Atmos. Sci. 1972, 29, 1041. [Google Scholar] [CrossRef]
- Bowman, J.; Krommes, J. The realizable Markovian closure and realizable test-field model II: Application to anisotropic drift-wave dynamics. Phys. Plasmas 1997, 4, 3895. [Google Scholar] [CrossRef]
- Herring, J.; Orszag, S.; Kraichnan, R.; Fox, D. Decay of two-dimensional homogeneous turbulence. J. Fluid Mech. 1974, 66, 417. [Google Scholar] [CrossRef]
- Pouquet, A.; Lesieur, M.; André, J.; Basdevant, C. Evolution of high Reynolds number two-dimensional turbulence. J. Fluid Mech. 1975, 72, 305. [Google Scholar]
- Kraichnan, R.; Herring, J. A strain-based Lagrangian-History turbulence. J. Fluid Mech. 1978, 88, 355. [Google Scholar] [CrossRef]
- McComb, W. The Physics of Fluid Turbulence; Oxford engineering science series 25; Clarendon Press: Oxford, 1990. [Google Scholar]
- Frederiksen, J.; Davies, A. Dynamics and spectra of cumulant update closures for two-dimensional turbulence. Geophys. Astrophys. Fluid Dyn. 2000, 92, 197. [Google Scholar] [CrossRef]
- Frederiksen, J.; Davies, A. The regularized DIA closure for two-dimensional turbulence. Geophys. Astrophys. Fluid Dyn. 2004, 98, 203. [Google Scholar] [CrossRef]
- Kraichnan, R. Instability in fully developed turbulence. Phys. Fluids 1970, 13, 569. [Google Scholar] [CrossRef]
- Leith, C. Theoretical skill of Monte Carlo forecasts. Mon. Wea. Rev. 1974, 102, 409. [Google Scholar] [CrossRef]
- Métais, O.; Lesieur, M. Statistical predictability of decaying turbulence. J. Atmos. Sci. 1986, 43, 857. [Google Scholar] [CrossRef]
- O’Kane, T.; Frederiksen, J. A comparison of statistical dynamical and ensemble prediction methods during blocking. J. Atmos. Sci. 2008, 65, 426. [Google Scholar] [CrossRef]
- Frederiksen, J. Renormalized closure theory and subgrid-scale parameterizations for two-dimensional turbulence., volume Nonlinear Dynamics: From Lasers to Butterflies of World Scientific Lecture Notes in Complex Systems. World Scientific Press, 2003. [Google Scholar]
- Wyld, H. Formulation of the theory of turbulence in an incompressible fluid. Annal. Phys. 1961, 14, 143. [Google Scholar] [CrossRef]
- Lee, L. A formulation of the theory of isotropic hydromagnetic turbulence in an incompressible fluid. Annal. Phys. 1965, 32, 292–321. [Google Scholar] [CrossRef]
- Martin, P.; Siggia, E.; Rose, H. Statistical dynamics of classical systems. Phys. Rev. A 1973, 8, 423. [Google Scholar] [CrossRef]
- Phythian, R. The operator formalism of classical statistical dynamics. J. Phys. A 1975, 8, 1423. [Google Scholar] [CrossRef]
- Phythian, R. The functional formalism of classical statistical dynamics. J. Phys. A 1977, 10, 777. [Google Scholar] [CrossRef]
- Jouvet, B.; Phythian, R. Quantum aspects of classical and statistical fields. Phys. Rev. A 1979, 19, 1350. [Google Scholar] [CrossRef]
- Jensen, R. Functional integral approach to classical statistical dynamics. J. Stat. Phys. 1981, 25, 183–210. [Google Scholar] [CrossRef]
- Ogura, Y. A consequence of the zero fourth cumulant approximation in the decay of isotropic turbulence. J. Fluid Mech. 1963, 16, 33. [Google Scholar] [CrossRef]
- Orszag, S. Statistical theory of turbulence. Balian, R., Peube, J.-L., Eds.; In Fluid Dynamics 1973Les Houches Summer School of Theoretical Physics, page 237; Gordan and Breech: London, 3rd edition; 1977. [Google Scholar]
- Herring, J.; Kraichnan, R. Statistical Models of Turbulence; Springer, 1972. [Google Scholar]
- Kraichnan, R. Decay of isotropic turbulence in the direct-interaction approximation. Phys. Fluids 1964, 7, 1030. [Google Scholar] [CrossRef]
- Herring, J.; Kerr, R. Development of enstrophy and spectra in numerical turbulence. Phys. Fluids 1993, 5, 2792. [Google Scholar] [CrossRef]
- Rose, H. An efficient non-Markovian theory of non-equilibrium dynamics. Physica D 1985, 14, 216. [Google Scholar] [CrossRef]
- Lesieur, M. Turbulence in FluidsFluid mechanics and its applications; Kluwer academic publishers, 3rd edition edition; 1997. [Google Scholar]
- O’Kane, T. The statistical dynamics of geophysical flows: An investigation of two-dimensional turbulent flow over topography. PhD Thesis, Monash University, 2003. [Google Scholar]
- O’Kane, T.; Frederiksen, J. The QDIA and regularized QDIA closures for inhomogeneous turbulence over topography. J. Fluid Mech. 2004, 504, 133–165. [Google Scholar] [CrossRef]
- Krommes, J. Fundamental statistical descriptions of plasma turbulence in magnetic fields. Phys. Rep. 2002, 360, 1. [Google Scholar] [CrossRef]
- Kraichnan, R. Diagonalizing approximation for inhomogeneous turbulence. Phys. Fluids 1964, 7, 1169. [Google Scholar] [CrossRef]
- Kraichnan, R. Lagrangian History closure approximation for turbulence. Phys. Fluids 1965, 8, 575. [Google Scholar] [CrossRef]
- Kaneda, Y. Renormalized expansions in the theory of turbulence with the use of the Lagrangian position approximation. Phys. Fluids 1981, 107, 131. [Google Scholar]
- Kaneda, Y. Lagrangian renormalized approximation of turbulence. Fluid Dyn. Res. 2007, 39, 526. [Google Scholar] [CrossRef]
- Herring, J. On the statistical theory of two-dimensional topographic turbulence. J. Atmos. Sci. 1977, 34, 1731. [Google Scholar] [CrossRef]
- Holloway, G. A spectral theory of nonlinear barotropic motion above irregular topography. J. Phys. Oceanogr. 1978, 8, 414. [Google Scholar] [CrossRef]
- Holloway, G. Systematic forcing of large-scale geophysical flows by eddy-topographic interaction. J. Phys. Oceanogr. 1987, 184, 463. [Google Scholar]
- Kraichnan, R. Test-field model for inhomogeneous turbulence. J. Fluid Mech. 1972, 56, 287. [Google Scholar] [CrossRef]
- Frederiksen, J. Subgrid-scale parameterizations of eddy-topographic force, eddy viscosity, and stochastic backscatter for flow over topography. J. Atmos. Sci. 1999, 56, 1481. [Google Scholar] [CrossRef]
- Frederiksen, J.; O’Kane, T. Inhomogeneous closure and statistical mechanics for Rossby wave turbulence over topography. J. Fluid Mech. 2005, 539, 137–165. [Google Scholar] [CrossRef]
- O’Kane, T.; Frederiksen, J. Statistical dynamical subgrid-scale parameterizations for geophysical flows. Phys. Scr. 2008. accepted. [Google Scholar] [CrossRef]
- O’Kane, T.; Frederiksen, J. Comparison of statistical dynamical, square root and ensemble Kalman filters. Entropy 2008. page accepted. [Google Scholar] [CrossRef]
- Hasselmann, K. Feynman diagrams and interaction rules for wave-wave scattering processes. Rev. Geophys. 1966, 4, 1. [Google Scholar] [CrossRef]
- Carnevale, G.; Frisch, U.; Salmon, R. H theorems in statistical fluid dynamics. J. Phys. A: Math. Gen. 1981, 14, 1701. [Google Scholar] [CrossRef]
- Biven, L.; Connaughton, C.; Newell, A. Structure functions, cumulants and breakdown criteria for wave turbulence., volume Nonlinear Dynamics: From Lasers to Butterflies of World Scientific Lecture Notes in Complex Systems. World Scientific Press, 2003. [Google Scholar]
- Frederiksen, J.; Bell, R. Statistical dynamics of internal gravity wave turbulence. Geophys. Astrophys. Fluid Dynamics 1983, 26, 257. [Google Scholar] [CrossRef]
- Frederiksen, J.; Bell, R. Energy and entropy evolution of internal gravity waves and turbulence. Geophys. Astrophys. Fluid Dynamics 1984, 28, 171. [Google Scholar] [CrossRef]
- Kleeman, R. Measuring dynamical prediction utility using relative entropy. J. Atmos. Sci. 2002, 59, 2057. [Google Scholar] [CrossRef]
- Rhines, P. Waves and turbulence on a β-plane. J. Fluid Mech. 1975, 69, 417. [Google Scholar] [CrossRef]
- Holloway, G.; Hendershott, M. Stochastic closure for nonlinear Rossby waves. J. Fluid Mech. 1977, 82, 747. [Google Scholar] [CrossRef]
- Carnevale, G. Statistical features of the evolution of two-dimensional turbulence. J. Fluid Mech. 1982, 122, 143. [Google Scholar] [CrossRef]
- Vallis, G.; Maltrud, M. Generation of mean flows and jets on a beta-plane and over topography. J. Phys. Oceanogr. 1993, 23, 1346. [Google Scholar] [CrossRef]
- Maltrud, M.; Vallis, G. Energy and enstrophy transfer in numerical simulations of two-dimensional turbulence. Phys. Rev. Lett. 1990, 65, 2137. [Google Scholar] [CrossRef]
- Huang, H.; Robinson, W. Two-dimensional turbulence and persistent zonal jets in a global barotropic model. J. Atmos. Sci. 2004, 55, 611. [Google Scholar] [CrossRef]
- Galperin, B.; Sukoriansky, S.; Huang, H.-P. Universal n−5 spectrum of zonal flows on giant planets. Phys. Fluids. 2001, 13, 1545. [Google Scholar] [CrossRef]
- Sukoriansky, S.; Galperin, B.; Dikovskaya, N. Universial spectrum of two-dimensional turbulence on a rotating sphere and some basic features of atmospheric circulation on giant planets. Phys. Rev. Lett. 2002, 89, 124501-1. [Google Scholar] [CrossRef] [PubMed]
- Smagorinsky, J. General circulation experiments with the primitive equations. i. the basic experiment. Mon. Wea. Rev. 1963, 91, 99. [Google Scholar] [CrossRef]
- Manabe, S.; Hahn, D.; Jr., J. H. Climate simulation with gfdl spectral models of the atmosphere: Effect of spectral truncation. GARP Pub. Ser. 1979, 22, 41. [Google Scholar]
- Laursen, L.; Eliasen, E. On the effects of damping in an atmospheric general circulation model. Tellus 1989, 41A, 385. [Google Scholar] [CrossRef]
- Koshyk, J.; Boer, G. Parameterization of dynamical subgrid-scale processes in a spectral GCM. J. Atmos. Sci. 1995, 52, 965. [Google Scholar] [CrossRef]
- Kaas, E.; Guldberg, A.; May, W.; Deque, M. Using tendency errors to tune the parameterization of unresolved dynamical scale interactions in atmosperic general circulation models. Tellus A 1999, 51, 612. [Google Scholar] [CrossRef]
- Frederiksen, J.; Dix, M.; Davies, A. The effects of closure-based eddy diffusion on the climate and spectra of a GCM. Tellus 2003, 55A, 31. [Google Scholar] [CrossRef]
- Kraichnan, R. Eddy viscosity in two and three dimensions. J. Atmos. Sci. 1976, 33, 1521. [Google Scholar] [CrossRef]
- Rose, H. Eddy diffisuvity, eddy noise and subgrid-scale modelling. J. Fluid Mech. 1977, 81, 719. [Google Scholar] [CrossRef]
- Leslie, D.; Quarini, G. The application of turbulence theory to the formulation of subgrid modelling procedures. J. Fluid Mech. 1979, 91, 65. [Google Scholar] [CrossRef]
- Chollet, J.; Lesieur, M. Parameterization of small scales of three-dimensional isotropic turbulence utilizing spectral closures. J. Atmos. Sci. 1981, 38, 2747. [Google Scholar] [CrossRef]
- Leith, C. Stochastic backscatter in a subgrid model: Plane shear mixing layer. Phys. Fluids. A 1990, 2, 297. [Google Scholar] [CrossRef]
- Chasnov, J. Simulation of the Kolmogorov inertial subrange using an improved subgrid model. Phys. Fluids A 1991, 3, 188. [Google Scholar] [CrossRef]
- Domaradzki, J.; Liu, W.; Bracket, M. An analysis of subgrid-scale interactions in numerically simulated isotropic turbulence. Phys. Fluids A 1993, 5, 1747. [Google Scholar] [CrossRef]
- McComb, W.; Watt, A. Conditional averaging procedure for the elimination of the small-scale modes from incompressible fluid turbulence at high Reynolds numbers. Phys. Rev, Lett. 1990, 65, 3281. [Google Scholar] [CrossRef] [PubMed]
- McComb, W.; Johnson, C. Conditional mode elimination and scale-invariant dissipation in isotropic turbulence. Physica A 2001, 292, 346. [Google Scholar] [CrossRef]
- McComb, W.; Hunter, A.; Johnson, C. Conditional mode elimination and the subgrid-modelling problem for isotropic turbulence. Phys. Fluids 2001, 13, 2030. [Google Scholar] [CrossRef]
- Schilling, O.; Zhou, Y. Analysis of spectral eddy viscosity and backscatter in incompressible isotropic turbulence using statistical closure. Phys. Fluids 2002, 14, 1244. [Google Scholar] [CrossRef]
- Frederiksen, J.; Kepert, S. Dynamical subgrid-scale parameterizations from direct numerical simulations. J. Atmos. Sci. 2006, 63, 3006. [Google Scholar] [CrossRef]
- Palmer, T. A nonlinear dynamical perspective on model error: A proposal for nonlocal stochastic-dynamic parameterization in weather and climate prediction models. Quart. J. R. Met. Soc. 2001, 127, 279. [Google Scholar] [CrossRef]
- Shutts, G. A kinetic energy backscatter algorithm for use in ensemble prediction systems. Quart. J. R. Met. Soc. 2005, 131, 3079. [Google Scholar] [CrossRef]
- Seiffert, R.; Blender, R.; Fraedrich, K. Subscale forcing in a global atmospheric circulation model and stochastic parameterisation. Quart. J. R. Met. Soc. 2006, 132, 1. [Google Scholar] [CrossRef]
- Seiffert, R.; vonStorch, J.-S. Impact of atmospheric small-scale fluctuations on climate sensitivity. Geophys. Res. Lett. 2008, 35, L10704, 1–5. [Google Scholar] [CrossRef]
- Berner, J.; Doblas-Reyes, F.; Palmer, T.; Shutts, G.; Weisheimer, W. Impact of quasi-stochastic cellular automaton backscatter on the systematic error and seasonal prediction skill of a global climate model. Phil. Trans. R. Soc. A 2008, 366, 2561. [Google Scholar] [CrossRef] [PubMed]
- Majda, A.; Franzke, C.; Khouider, B. An applied mathematics perspective on stochastic modelling for climate. Phil. Trans. Roy. Soc. A 2008, 366, 2429. [Google Scholar] [CrossRef] [PubMed]
- Holloway, G. Representing topographic stress for large-scale ocean models. J. Phys. Oceanogr. 1992, 22, 1033. [Google Scholar] [CrossRef]
- Cummings, P.; Holloway, G. On eddy-topographic stress representation. J. Phys. Oceanogr. 1993, 24, 700. [Google Scholar] [CrossRef]
- Alvarez, A.; Tintore, G.; Holloway, G.; Eby, M.; Beckers, J. Effect of topographic stress on the circulation in the western Mediterranean. J. Geophys. Res. 1994, 99, 16 053. [Google Scholar] [CrossRef]
- Holloway, G.; Sou, T.; Eby, M. Dynamics of circulation of the Japan Sea. J. Mar. Res. 1995, 53, 539. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal relations in irreversible processes. i. Phys. Rev. 1951, 37, 405. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal relations in irreversible processes. ii. Phys. Rev. 1951, 38, 2265. [Google Scholar] [CrossRef]
- Prigogine, I. Le domaine de validite de la thermodynamique des phenomes irreversibles. Physica 1949, 15, 272. [Google Scholar] [CrossRef]
- Prigogine, I. Introduction to Thermodynamics of Irreversible Processes; Springfield, 1955. [Google Scholar]
- Kohler, M. Behandlung von nightgleichgewicht vorgangen mit hilfe eines extremalprinzips. Z. Physik 1948, 124, 772. [Google Scholar] [CrossRef]
- Ziegler, H. Introduction to Thermomechanics; North-Holland, Amsterdam, 1983. [Google Scholar]
- Paltridge, G. Global dynamics - a system of minimum entropy exchange. Quart. J. R. Met. Soc. 1975, 101, 475. [Google Scholar] [CrossRef]
- Jones, W. Variational principles for entropy production and predictive statistical mechanics. J. Phys. A: Math. Theor. 1983, 16, 3629. [Google Scholar] [CrossRef]
- Dewar, R. Information theory explanation of the fluctuation theorem, maximum entropy production and self-organized criticality in non-equilibrium stationary states. J. Phys. A: Math. Theor. 2003, 36, 631. [Google Scholar] [CrossRef]
- Dewar, R. Maximum entropy production and the fluctuation theorem. J. Phys. A: Math. Theor. 2005, 38, L371. [Google Scholar] [CrossRef]
- Jaynes, E. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620. [Google Scholar] [CrossRef]
- Kazantsev, E.; Sommeria, J.; Verron, J. Subgrid-scale eddy parameterization by statistical mechanics in a barotropic ocean model. J. Phys. Oceanogr. 1998, 28, 1017. [Google Scholar] [CrossRef]
- Polyakov, I. An eddy parameterization based on maximum entropy production with application to modeling of the Arctic ocean circulation. J. Phys. Oceanogr. 2001, 31, 2255. [Google Scholar] [CrossRef]
- Holloway, G. From classical to statistical ocean dynamics. Surv. Geophys. 2004, 25, 203. [Google Scholar] [CrossRef]
- Barbera, E. On the principle of minimal entropy production for Navier-Stokes-Fourier fluids. Continuum Mech. Thermodyn. 1999, 11, 327. [Google Scholar] [CrossRef]
- Attard, P. Statistical mechanical theory for steady state systems. iv. variational principles. J. Chem. Phys. 2006, 125, 214502. [Google Scholar] [CrossRef] [PubMed]
- Bruers, S. A discussion on maximum entropy production and information theory. J. Phys. A: Math. Theor. 2007, 40, 7441. [Google Scholar] [CrossRef]
- Grinstein, G.; Linsker, R. Comments on a derivation and application of the ’maximum entropy production’ principle. J. Phys. A: Math. Theor. 2007, 40, 9717. [Google Scholar] [CrossRef]
- Martyushev, L.; Seleznev, V. Maximum entropy production principle in physics, chemistry and biology. Phys. Rep. 2006, 426, 1. [Google Scholar] [CrossRef]
- Dewar, R.; Hole, M.; McGann, M.; Mills, R.; Hudson, S. Relaxed plasma equilibria and entropy-related plasma self-organization principles. Entropy 2008. page accepted. [Google Scholar] [CrossRef]
- Prigogine, I.; Stengers, I. Order out of Chaos; Flamingo: London, 1985. [Google Scholar]
- Zidikheri, M.; Frederiksen, J.; O’Kane, T. Multiple equilibria and atmospheric blocking., volume Frontiers in Turbulence and Coherent Structures of World Scientific Lecture Notes in Complex Systems. World Scientific Press, 2007. [Google Scholar]
- Katz, A. Principles of Statistical Mechanics; Freeman, 1967. [Google Scholar]
- Hollingsworth, A.; Cubasch, U.; Tibaldi, S.; Brankovic, C.; Palmer, T.; Campbell, L. Mid-latitude atmospheric prediction on time scales of 10-30 days; Atmospheric and oceanic variability; Royal Meteorological Society, 1987. [Google Scholar]
- Piomelli, V.; Cabot, W.; Moin, P.; Lee, S. Subgrid-scale backscatter in turbulent and transitional flows. Phys. Fluids A 1991, 3, 1766. [Google Scholar] [CrossRef]
© 2008 by the authors. Licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Frederiksen, J.S.; O’Kane, T.J. Entropy, Closures and Subgrid Modeling. Entropy 2008, 10, 635-683. https://doi.org/10.3390/e10040635
Frederiksen JS, O’Kane TJ. Entropy, Closures and Subgrid Modeling. Entropy. 2008; 10(4):635-683. https://doi.org/10.3390/e10040635
Chicago/Turabian StyleFrederiksen, Jorgen S., and Terence J. O’Kane. 2008. "Entropy, Closures and Subgrid Modeling" Entropy 10, no. 4: 635-683. https://doi.org/10.3390/e10040635




