1. Introduction
Use of an external magnetic field is of considerable importance in many industrial applications, particularly as a control mechanism in material manufacturing. Homogeneity and quality of single crystals grown from doped semiconductor melts is of interest to manufacturers of electronic chips. One of the main purposes of electromagnetic control is to stabilize the flow and suppress oscillatory instabilities, which degrades the resulting crystal. Oreper and Szekely [
1] showed that the magnetic field suppresses the natural convection currents and the magnetic field strength is one of the most important factors for crystal formation. As a consequence there has been increased interest in the flows of electrically conducting fluid in cavities subjected to external magnetic field. For an electrically conducting fluid exposed to a magnetic field, Lorentz force is also active and interacts with the buoyancy force in governing the flow and temperature fields. Rudraiah
et al. [
2] investigated the effect of surface tension on buoyancy driven flow of an electrically conducting fluid in a square cavity in presence of a vertical transverse magnetic field to see how this force damps hydrodynamic movements, since, this is required to enhance crystal purity, increase compositional uniformity and reduce defect density. Al-Najem
et al. [
3] used the power control volume approach to determine the flow and temperature fields under a transverse magnetic field in a titled square enclosure with isothermal vertical walls and adiabatic horizontal walls at Prandtl number of 0.71. They showed that the suppression effect of the magnetic field on convection currents and heat transfer is more significant for low inclination angles and high Grashof numbers. Ishak
et al. [
4] numerically studied a steady two-dimensional flow of an electrically conducting fluid due to a stretching cylindrical tube. They showed that Nusselt number increases as Prandtl number increases (from
Pr = 0.7 to
Pr = 7). Moreover, the effect of the magnetic field is found to be more pronounced for fluids with smaller Prandtl number (
Pr = 0.7), since fluids with smaller Prandtl number have larger thermal diffusivity. Ece and Büyük [
5] investigated the influence of a magnetic field in an inclined rectangular enclosure heated from the left vertical wall and cooled from the top wall, while the other walls are kept adiabatic for the case of a laminar natural convection flow of a fluid characterized by
Pr = 1, which is an approximate value for most gases. They showed that the flow characteristics and therefore the convection heat transfer depend strongly upon the strength and direction of the magnetic field, the aspect ratio and the inclination of the enclosure. Circulation and convection become stronger with increasing Grashof number but they are significantly suppressed by the presence of a strong magnetic field. Magnetic field significantly reduces the local Nusselt number by suppressing the convection currents. Natural convection of low Prandtl number fluid in the presence of a magnetic field was numerically studied by Ozoe and Maruo [
6], they obtained correlations for the Nusselt number in terms of Rayleigh, Prandtl and Hartmann numbers. Rudraiah
et al. [
7] numerically investigated the effect of a transverse magnetic field on natural convection flow inside a rectangular enclosure with isothermal vertical walls and adiabatic horizontal walls and found out that a circulating flow is formed with a relatively weak magnetic field and that the convection is suppressed and the rate of convective heat transfer is decreased when the magnetic field strength increases. Alchaar
et al. [
8] numerically investigated the natural convection in a shallow cavity heated from below in the presence of an inclined magnetic field and showed that the convection modes inside the cavity strongly depend on both the strength and orientation of the magnetic field and that horizontally applied magnetic field is the most effective in suppressing the convection currents.
Ikezoe
et al. [
9] have presented many interesting phenomena occurred in the magnetic field such as the levitation of a water droplet by strong magnetic field, driving of air flow due to magnetic field,
etc. Wakayama [
10] and Wakayama
et al. [
11,
12] found very interesting phenomena such as jet stream of nitrogen gas into air (Wakayama jet) in a steeply decreasing magnetic field, enhancement of combustion flames and sustaining flame under microgravity. Filar
et al. [
13] numerically computed three-dimensional convection of air in a vertical cylinder isothermally heated and cooled from a side wall in both magnetic and gravity fields. A single electric coil was placed around the cylinder to generate a magnetic field. It was found that the flow mode and heat transfer rate can be controlled by magnetic field. Further, axi-symmetric stable convection or even near the conduction state was obtained when the coil is located near the top plate of the cylinder, whereas strong and oscillatory convection was resulted when the magnetic coil is located near the bottom plate of the cylinder. Teamah [
14] numerically studied steady heat and mass transfer by natural convection flow of a heat generating fluid in presence of a transverse magnetic field in a rectangular enclosure at fixed values of aspect ratio (
A = 2), Lewis number (
Le = 1) and Prandtl number (
Pr = 0.7). It was found that magnetic field tends to reduce heat transfer and fluid circulation within the enclosure. For Hartmann number
Ha > 20, average Nusselt and Sherwood numbers have constant values over a range of thermal Rayleigh number, this range increases with increasing Hartmann number. Tsai
et al. [
15] numerically studied the effects of variable viscosity and thermal conductivity on heat transfer for hydromagnetic flow over a continuous moving porous plate with ohmic heating. They showed that for
Pr = 0.7, the fluid velocity decreases, whereas the temperature profile increases with increasing in magnetic field. The study showed that temperature increases with an increasing in thermal conductivity parameter and decreasing Prandtl number at fixed values of magnetic parameter and Eckert number (studied Prandtl numbers are 0.7 and 6.7 which corresponds to air and water, respectively). The effect of the variable viscosity on velocity and temperature profiles for air (
Pr = 0.7) and water (
Pr = 6.7) at constant values of magnetic parameter (
M = 1), Eckert number (
Ec = 0.5) and thermal conductivity parameter (
S = 1), shows that velocity and temperature for air is more obviously than for liquid water. Bararnia
et al. [
16] employed a Homotopy analysis method (HAM) to investigate momentum, heat and mass transfer characteristics of MHD natural convection flow for the case of an electrically conducting and heat generation fluid over a porous surface immersed in a porous medium. They showed that at fixed imposed magnetic field, the increase in Prandtl number from liquid metal to liquid passing through gas (
Pr = 0.1, 0.5, 0.7, 1 and 10) tends to reduce thermal boundary layer along the plate. This yields a reduction in the fluid temperature. Thus, the higher Prandtl number means more viscous fluid which increases boundary layer thickness and then causes reduction in shear stress. Alam
et al. [
17] numerically studied Dufour and Soret effects on two-dimensional steady combined free-forced convective and mass transfer flow of a viscous, incompressible and electrically conducting fluid over an isothermal semi-infinite vertical flat plate under the influence of transversely applied magnetic field. It was shown that (the fluid mixture is characterized by a Prandtl number
Pr = 0.71 and a Schmidt number
Sc = 0.22) the increase of magnetic field leads to the decrease of velocity field indicating that magnetic field retards the flow motion. Inversely, the increase of magnetic field induces the augmentation of both temperature and concentration distributions.
Study of convective flow in rotating system is of considerable importance in many industrial, geophysical and engineering applications. In this context, Singh
et al. [
18] studied a hydromagnetic convective flow of an incompressible viscous liquid over an accelerated porous plate. The whole system is in a state of solid body rotation. Numerical values of Prandtl number are chosen to be
Pr = 0.71,
Pr = 7.0 and
Pr = 11.4, which corresponds to air, water at 20 °C and water at 4 °C, respectively. They found that an increase in magnetic field decreases the velocity field and that the increase in Prandtl number decreases the temperature field. Further, an increase in rotation parameter increases the velocity and the temperature fields. A combined free and forced convection flow of an electrically conducting fluid in a channel in presence of a transverse magnetic field is of special technical significance because of its frequent occurrence in many industrial applications such as geothermal reservoirs, cooling of nuclear reactors, thermal insulation and petroleum reservoirs. These types of problem also arise in electronic packages, microelectronic devices during their operations. For more details reader can see [
19,
20,
21,
22] as examples.
Efficient utilization of energy is the primary objective in the design of any thermodynamic system. This can be achieved by minimizing entropy generation in processes. The theoretical method of entropy generation has been used in the specialized literature to treat external and internal irreversibilities. The irreversibility phenomena, which are expressed by entropy generation in a given system, are related to heat transfer, mass transfer, viscous dissipation, magnetic field,
etc., Bejan [
23,
24,
25], Bejan
et al. [
26], Arpaci and Selamet [
27,
28], Arpaci [
29,
30], Arpaci and Esmaeeli [
31], Magherbi
et al. [
32,
33] and Abbassi
et al. [
34] have studied the influence of operating parameters on entropy generation in different flow configurations. They showed that the flow parameters might be chosen in order to minimize entropy generation inside the system. Salas
et al. [
35] analytically showed a way of applying entropy generation analysis for modelling and optimization of magnetohydrodynamic induction devices. Salas
et al. [
35] restricted their analysis to only Hartmann model flow in a channel. Mahmud and Fraser [
36] studied entropy generation in a fluid saturated porous cavity for laminar magnetohydrodynamic natural convection, where the magnetic force is assumed acting along the direction of the gravity force. It was found that increasing Hartmann number (
i.e., magnetic force), tends to retard the fluid motion, both average Nusselt and dimensionless entropy generation numbers decrease with increasing Hartmann number and approach a limiting value (asymptotic value). For other configurations and/or geometrical situation flows, a detailed analysis of the second law of thermodynamics for fundamental problems of heat transfer is given by Mahmud and Fraser [
37]. Mahmud
et al. [
38] performed a thermodynamic analysis of steady mixed convection flow of an electrically conducting and heat-generating/absorbing fluid through a vertical channel in presence of a magnetic field applied normal to the flow direction. Thermophysical properties of the fluid are considered constant with a Prandtl number
Pr = 0.7. It was found that the increase in Hartmann number (
Ha) tends to slow down the fluid velocity in the channel for symmetric temperature at walls with a symmetric tendency of velocity profiles about the centreline of the channel. For asymmetric temperature at the walls, velocity profiles are not symmetric about the centreline of the channel and asymmetricity increases more as Hartmann number increases. In the case of symmetric temperature at the boundary, as Hartmann number increases, entropy generation decreases towards a minimum value at the centreline of the channel, then increases again. They numerically determined a correlation giving the value of the aspect ratio
α0 of the channel which corresponds to minimum entropy generation, and it is given by:
where
Gr and
Re are Grashof and Reynolds numbers, respectively.
The main objective of this work is to examine the influence of an external oriented magnetic field on entropy generation as well as on heat transfer and fluid flow in natural convection of two different fluids which are air (with Pr = 0.71) and liquid gallium (with Pr = 0.02) enclosed in a square cavity. The numerical resolution is based on control volume finite element method for resolving the governing equations in 2D approximation. Local and total irreversibilities are studied by using five independent parameters, which are: the Prandtl number, the inclination angle of the magnetic field, the irreversibility coefficients and Grashof and Hartman numbers. The behaviour of entropy generation in transient state and then entropy generation analysis in stationary state are studied. This procedure may enhance the reversible work done by the fluid and minimize the degraded energy expressed by entropy generation.
2. Governing Equations
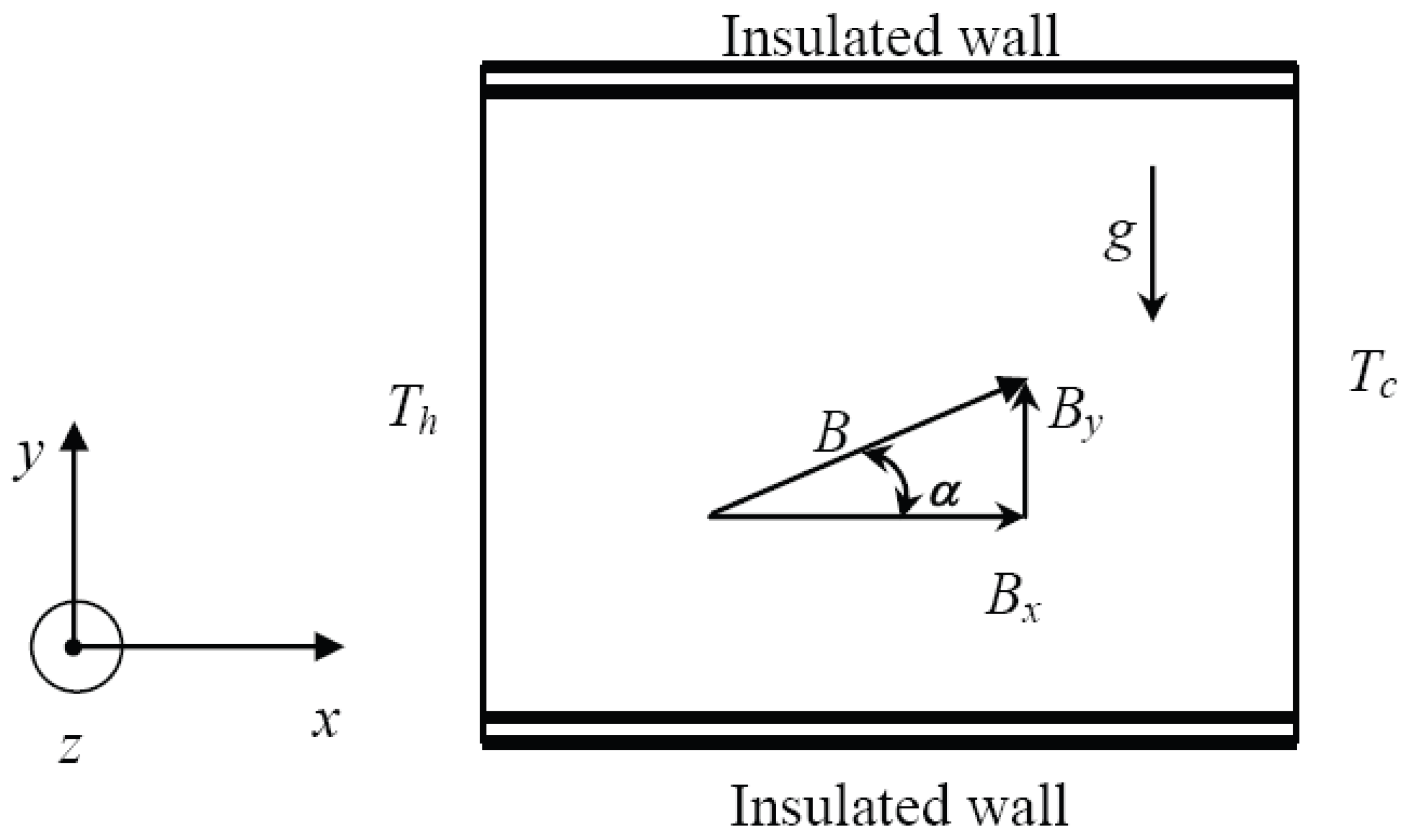
Laminar, incompressible boundary heat transfer by convective flow of a fluid such that its thermophysical properties remain constant is considered. x axis and y axis are in the plane and z axis is normal to it with velocity components (u, v, 0). A uniform magnetic field of strength B (Bx, By, 0) is applied and the magnetic Reynolds number (Rem = μeσeV0L0 << 1, where σe, μe, V0 and L0 are the magnetic permeability, the viscosity, the characteristic velocity and length, respectively) is assumed to be small so that the induced magnetic field is negligible in comparison to the applied magnetic field. Since there is no applied or polarization voltage imposed on the flow field, the electric field E = 0.
The right and the left walls are maintained at uniform temperatures
Tc and
Th, respectively, and are such that
Tc <
Th, horizontal walls are adiabatic as illustrated in
Figure 1. The cavity is permeated by the uniform oriented magnetic field
B =
Bxex +
Byey (where
Bx and
By are space independent) of constant magnitude
B0 =
and
ex and
ey are unit vectors in Cartesian coordinate system. The orientation of the magnetic field forms an angle
α with horizontal axis, such that tan
α =
By/Bx.
Figure 1.
Cavity configuration in presence of an oriented magnetic field.
Figure 1.
Cavity configuration in presence of an oriented magnetic field.
The electric current density and the electromagnetic force are defined as follows, respectively:
As mentioned above, the electric field is negligible, so that Equation (2) and Equation (3) are given by:
For an oriented magnetic field (which makes an inclination angle
α with respect to
x axis), and by taking into consideration the electromagnetic force components projected with respect to
x and
y directions, the continuity, change of linear momentum and energy equations in scalar form are written as follows:
CP is the isobaric specific heat of the fluid. Thus, the governing conservative equations of the mass, the momentum and the energy in their dimensionless variables take the following form:
momentum equation in
X direction:
momentum equation in
Y direction:
The governing equations are established on the basis of the following dimensionless variables:
Governing equations show that the flow is governed by the inclination angle of the electromagnetic force, the Prandtl number which characterizes the relative importance of viscous to thermal effects, the thermal Grashof number which approximates the ratio of the buoyancy force to the viscous force acting on the fluid, the magnetic field and the Hartmann number. Hartmann number indicates the relative importance of the electromagnetic force to the viscous force.
Boundary conditions of the problem are given by:
Initial conditions (
i.e., at
τ = 0) are:
It is reasonable to notice that there is no temperature gradient at initial state.
Once the numerical value of the temperature θ is calculated, the rate of heat flux in dimensionless form is given by Nusselt number that compares convection to conduction modes.
Equating the heat transfer by convection to the heat transfer by conduction at hot wall gives:
Introducing the dimensionless variables defined in Equation (14), into Equation (15), gives the local Nusselt number:
Consequently, the average Nusselt number is obtained by integrating the above local Nusselt number over the vertical hot wall:
5. Results and Discussions
Problems of natural convection flow are numerically, analytically and experimentally investigated by many authors. The main originality of the present paper is to study numerically the influence of an external oriented magnetic field on entropy generation in natural convection flow. As indicated above, the independent operating parameters of the considered problem are: the thermal Grashof number GrT, ranging between 103 and 105, the irreversibility coefficient related to fluid friction χ1, ranging between 10−4 and 10−2, the Hartmann number Ha, ranging between 0 and 100 and the inclination angle of the magnetic field α, ranging between 0° and 90°. Obviously, the irreversibility coefficient related to the magnetic field χ2, depends directly on χ1 and Ha. To be realistic, the numerical values of Prandtl number are chosen to be Pr = 0.71 and Pr = 0.02, which, correspond to air and liquid gallium, respectively. Liquid gallium is widely used in integrated circuits with optoelectronic devices, to dope semiconductors and produce solid-state devices like transistors, as a component in low-melting alloys and in some high temperature thermometers.
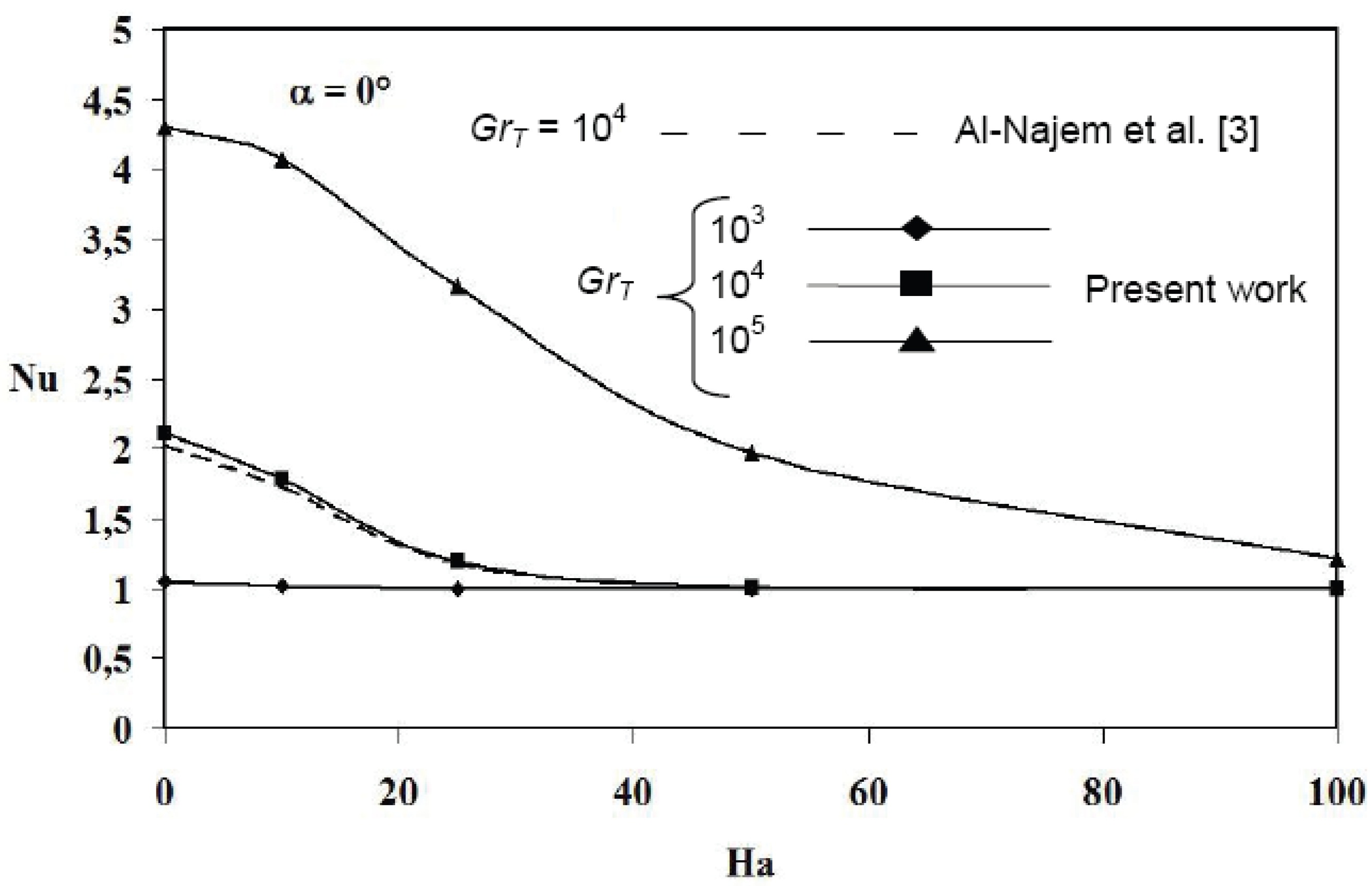
Figure 2 shows the variation of Nusselt number
versus Hartmann number for
α = 0° and
Pr = 0.71. Good agreement of our results and those found by Al-Najem
et al. [
3] is observed for
GrT = 10
4, heat transfer decreases as Hartmann number increases. It is important to notice that heat transfer is reduced to pure conduction mode as Hartmann number tends towards the value 100. Consequently, the magnetic field tends to suppress the convection and retards the fluid motion via the Lorentz force (magnetic force).
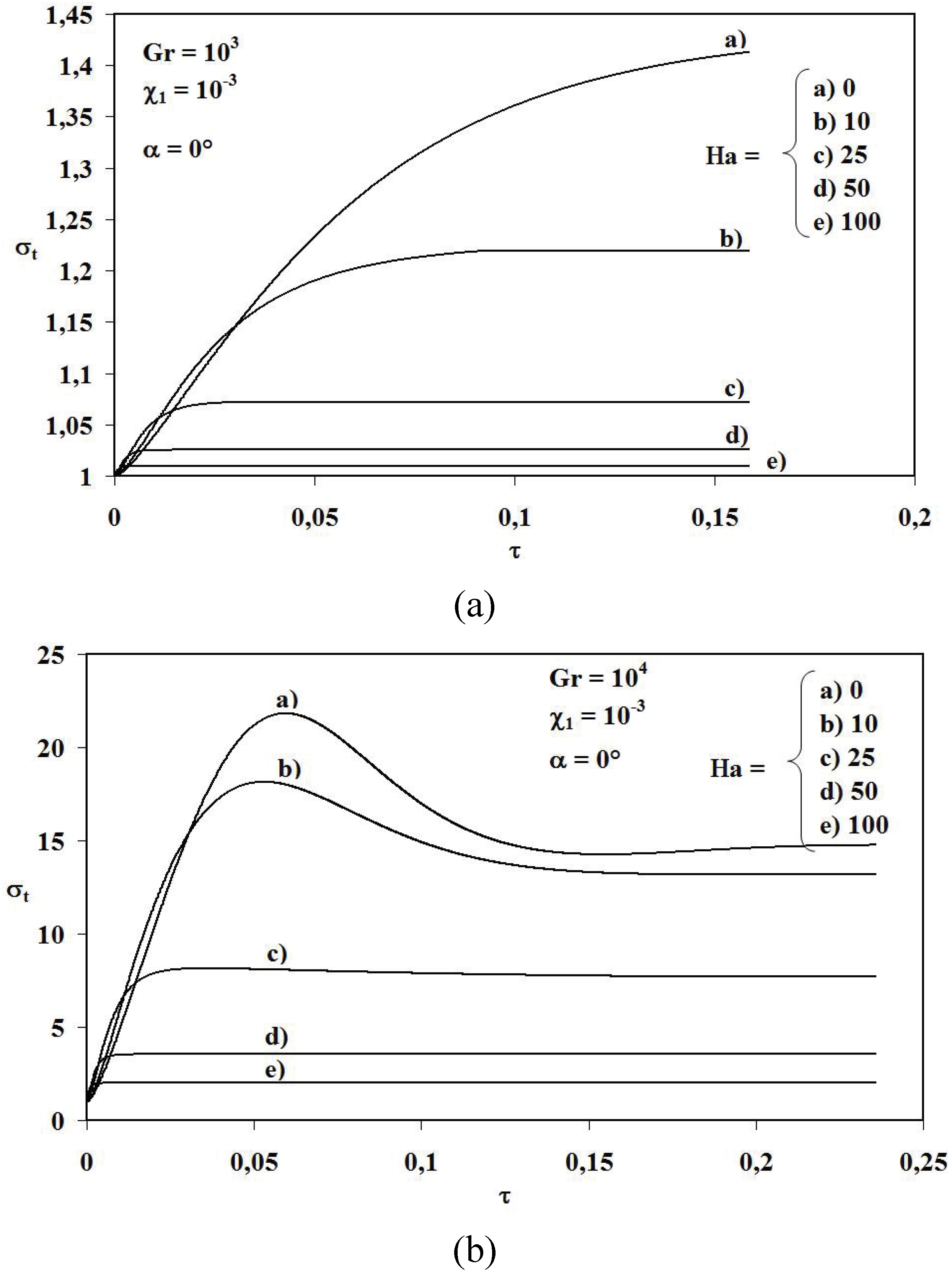
Transient entropy generation is then studied for fixed values of the Prandtl number, the inclination angle of the magnetic field (
α = 0°) and the irreversibility coefficient related to fluid friction (
χ1 = 10
−3) at different values of thermal Grashof and Hartmann numbers as illustrated in
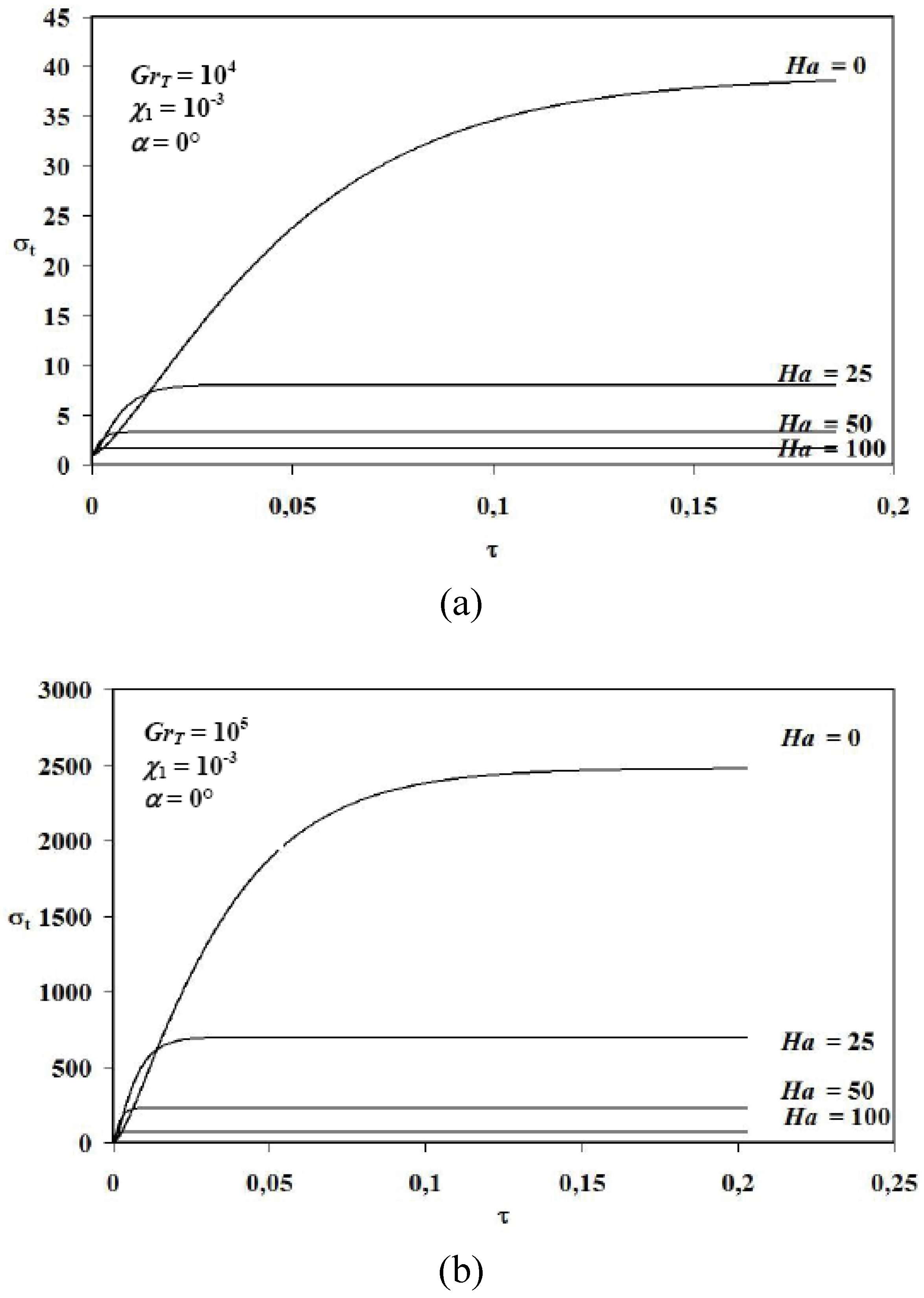
Figure 3 and
Figure 4. At
Pr = 0.71 and for
GrT ≤ 10
3,
Figure 3a shows that entropy generation magnitude increases from the value equal to unity at initial time towards an asymptotic value as time proceeds. Asymptotic value (which describes a stationary state) is rapidly achieved and considerably decreased in magnitude as Hartmann number increases. As a consequence, increasing Hartmann number induces the decrease of entropy generation. On increasing thermal Grashof number (
GrT = 10
4), same results are obtained as the previous case for higher values of Hartmann number (
i.e., 25 ≤
Ha ≤ 100) and inversely, an oscillatory behaviour of entropy generation is observed for lower values of Hartmann number (0 ≤
Ha ≤ 10) before achieving the stationary state (see
Figure 3b). For relatively considerable thermal Grashof number values (
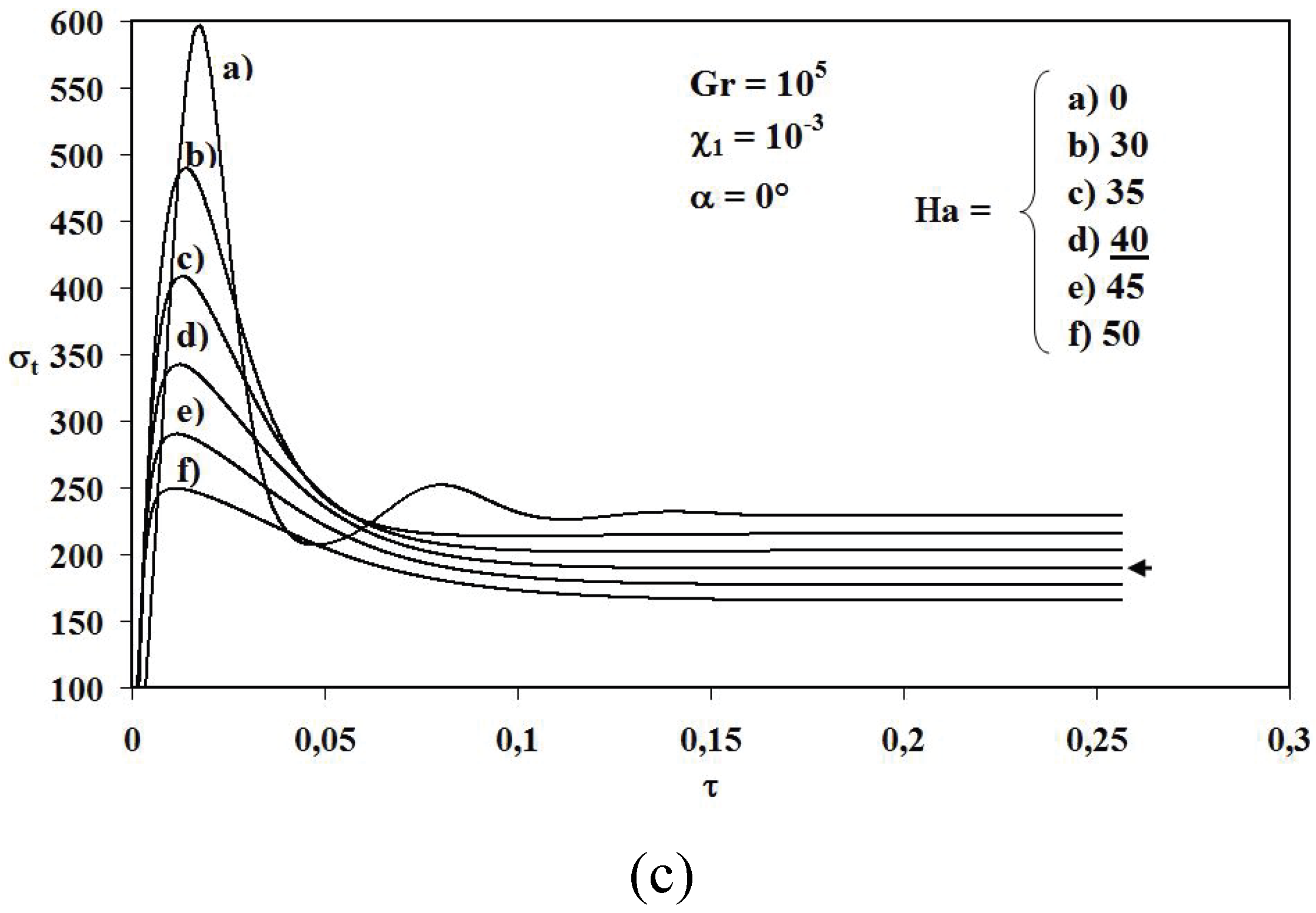
GrT ≥ 10
5),
Figure 3c shows an oscillatory behaviour of entropy generation at the very beginning of transient state for lower values of Hartmann number (0 ≤
Ha ≤ 35). A critical Hartmann number
Hac = 40 is obtained from which the oscillatory behaviour vanishes and entropy generation amplitude quickly reaches a maximum value before decreasing asymptotically towards the stationary state. As a consequence, amplitude and oscillation numbers of entropy generation are important as thermal Grashof number increases and Hartmann number decreases.
Figure 4 depicts transient entropy generation for
GrT = 10
4 and 10
5 at different Hartmann number values for
Pr = 0.02.
Figures 4a and 4b show that at fixed Hartmann number, entropy generation increases with time towards a constant value. As Hartmann number increases, asymptotic behaviour of entropy generation is quickly achieved with decreased amplitude of irreversibility. As a consequence, increasing Hartmann number induces the decrease of entropy generation. This is due to the fact that the magnetic field causes the fluid velocity deceleration and the decrease in heat transfer.
From
Figure 3 and
Figure 4, it is important to notice that at steady state, an increase in the value of Grashof number will increase the dominancy of the buoyancy force over the present magnetic field strength expressed by Hartmann number. As a consequence, for a fixed Hartmann number value, entropy generation magnitude increases as thermal Grashof number increases.
Figure 2.
Nusselt number versus Hartmann number for α = 0°.
Figure 2.
Nusselt number versus Hartmann number for α = 0°.
For
Pr = 0.71, fluctuations of total entropy generation
versus time for relatively higher thermal Grashof numbers show an oscillatory behaviour of fluid flow that depends on boundary conditions and the magnetic field amplitude. At the beginning of the transient state, heat transfer is mainly due to pure conduction, this is proved by the behaviour of isothermal lines which are parallel to active walls, as time proceeds, isothermal lines are gradually deformed due to convection mode which induces elongation of stream function lines. Consequently, a transition from a single cell towards double cells is obtained just before entropy generation reaches its maximum. This transition induces generation of internal waves in the velocity and temperature fields and than an oscillatory behaviour of entropy generation. Many previous works namely those of Ivey [
48], Schladow [
49] and Patterson and Armfield [
50] showed the existence of transient oscillations in enclosures consisting of two isothermal vertical walls and two adiabatic horizontal walls in absence of the magnetic field. In fact, Ivey [
48] showed that transition oscillations occurred because of an internal hydraulic jump with an increase of the horizontal intrusion layers. Transient oscillations consisting of two distinct boundary layer instabilities and whole cavity oscillations were observed by Schladow [
49]. The whole cavity oscillations were attributed to the horizontal pressure gradient established by changes in the intrusion temperature field. Similar observations are given by Patterson and Armfield [
50]. The two boundary layer oscillations were attributed to travelling wave instability on the boundary layer induced first by the leading edge effect of the vertical boundary layer and second by the impact of the horizontal intrusion from the opposing vertical wall with the boundary layer. The whole cavity oscillations are said to be caused by the splitting of the horizontal intrusion as it impacts the opposite wall. Liquid gallium (
Pr = 0.02) is characterized by higher thermal conductivity as compared to air, consequently heat transfer is practically dominated by conduction mode and then no oscillatory behaviour of fluid flow is observed at any of the studied Hartmann and thermal Grashof numbers. This is proved by the plot of transient heat transfer of both fluids at
GrT = 10
5 and
Ha = 0 as an illustrative example as shown in
Figure 5.
Figure 3.
Total dimensionless entropy generation (σt) versus dimensionless time for Pr = 0.71, α = 0° and χ1 = 10−3 at different Hartmann number values: (a) GrT = 103, (b) GrT = 104, (c) GrT = 105.
Figure 3.
Total dimensionless entropy generation (σt) versus dimensionless time for Pr = 0.71, α = 0° and χ1 = 10−3 at different Hartmann number values: (a) GrT = 103, (b) GrT = 104, (c) GrT = 105.
Figure 4.
Total dimensionless entropy generation (σt) versus dimensionless time for Pr = 0.02, α = 0°, and χ1 = 10−3 at different Hartmann number values: (a) GrT = 104, (b) GrT = 105.
Figure 4.
Total dimensionless entropy generation (σt) versus dimensionless time for Pr = 0.02, α = 0°, and χ1 = 10−3 at different Hartmann number values: (a) GrT = 104, (b) GrT = 105.
Figure 5.
Nusselt number versus time at GrT = 105, χ1 = 10−3 and Ha = 0 for Pr = 0.02 and 0.71.
Figure 5.
Nusselt number versus time at GrT = 105, χ1 = 10−3 and Ha = 0 for Pr = 0.02 and 0.71.
From thermodynamic viewpoint, the oscillatory behaviour of entropy generation at
Pr = 0.71 is observed when
GrT ≥ 10
4 for small Hartmann number values (
Figures 3b-3c). This result is consistent with the findings of Magherbi
et al. [
51] when
GrT ≥ 10
4 in absence of magnetic field. Magherbi
et al. [
51] showed that steady state is relatively far from equilibrium state, thus the system takes a spiral approach towards the stationary state corresponding to an oscillation of entropy generation over time. In this case the Prigogine’s theorem [
52] is not verified and the system evolves in the non-linear branch of thermodynamics for irreversible processes. The asymptotic behaviour of entropy generation observed for
GrT ≤ 10
3 (at any Hartmann number), for 10
3 <
GrT ≤ 10
4 (when
Ha ≥ 10) and for
GrT = 10
5 (when
Ha ≥ 40), shows that the system evolves in the linear branch of thermodynamics for irreversible processes, where the famous Onsager reciprocity relations are applicable. In these cases, the stationary state is sufficiently close to the equilibrium state, as a consequence, entropy generation, quickly reaches a maximum value, then tends towards a constant value. In order to have clear idea,
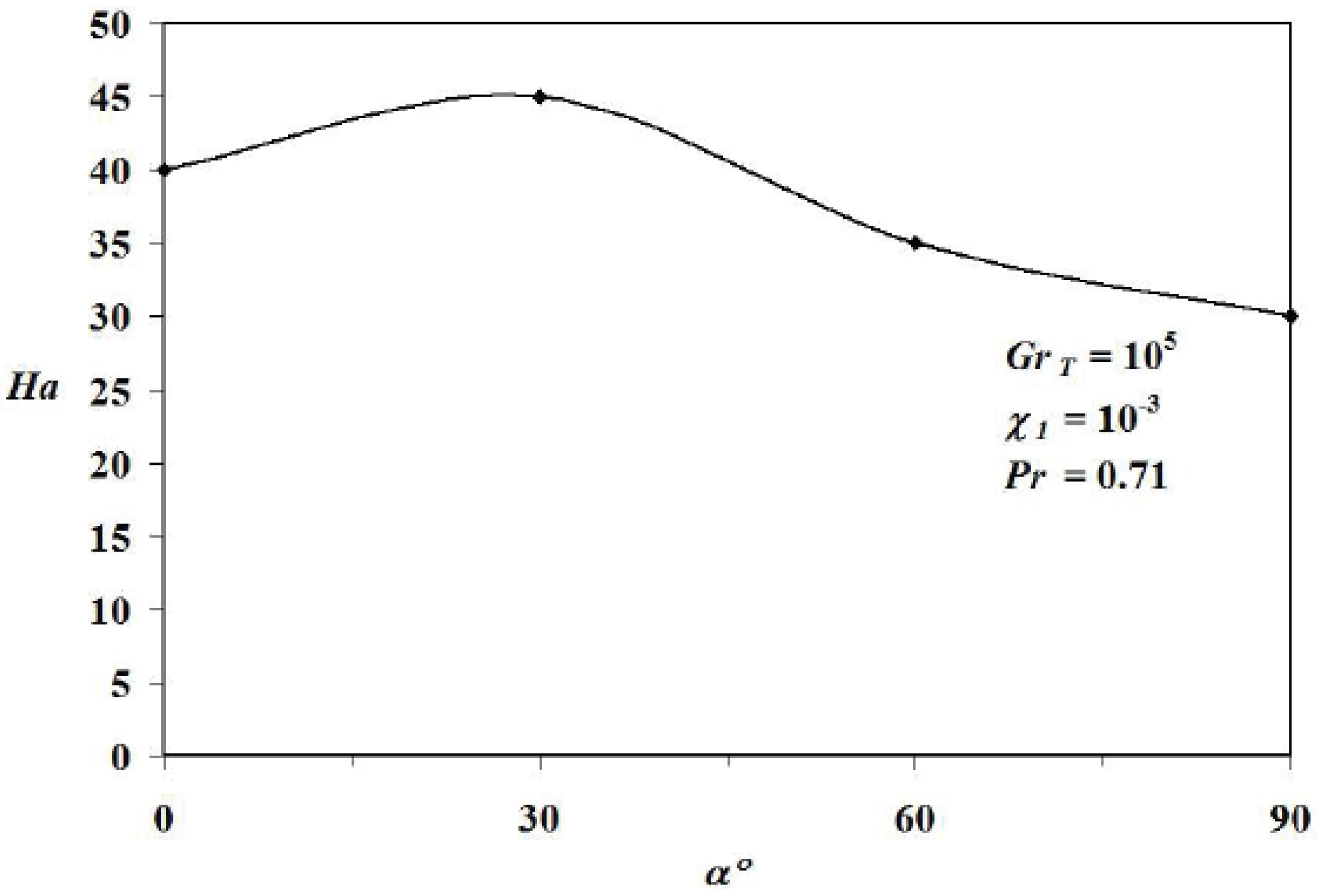
Figure 6 shows critical values of Hartmann number
versus the inclination angle of the magnetic field for a fixed thermal Grashof number (
GrT = 10
5). For
Ha >
Hac, the system evolves in the linear branch of thermodynamics of irreversible processes. Further, for 0° ≤
α ≤ 90°, it was found that maximum
Hac (= 45) is obtained at
α = 30° (see
Figure 6), this indicates that the stationary regime is far from the equilibrium state as compared to other inclination angle values of the magnetic field. In this case,
Hac = 30, 35 and 40 for
α = 90°, 60° and 0°, respectively. As an important conclusion, increasing the inclination angle of the magnetic field (30° ≤
α ≤ 90°) tends to decrease critical Hartmann number, and consequently to decrease transient oscillatory behaviour of entropy generation.
As mentioned above, no oscillatory behaviour is obtained for transient entropy generation at
Pr = 0.02 as compared to the situation when
Pr = 0.71 for the studied Grashof and Hartmann numbers. This is possible since low Prandtl number means higher thermal conductivity, consequently, fluid temperature increases as Prandtl number decreases (see Equation (13)). This is confirmed by Singh
et al. [
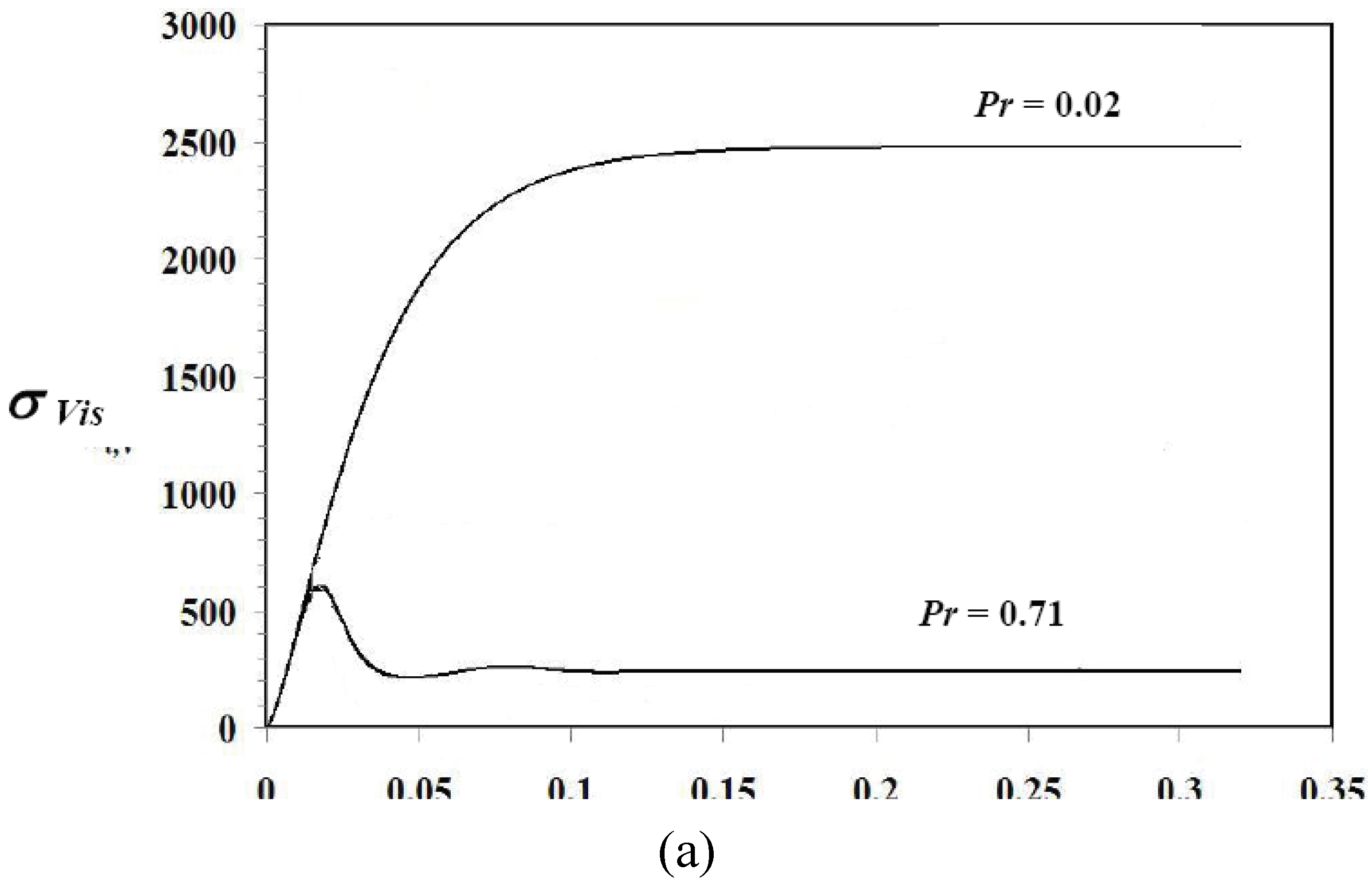
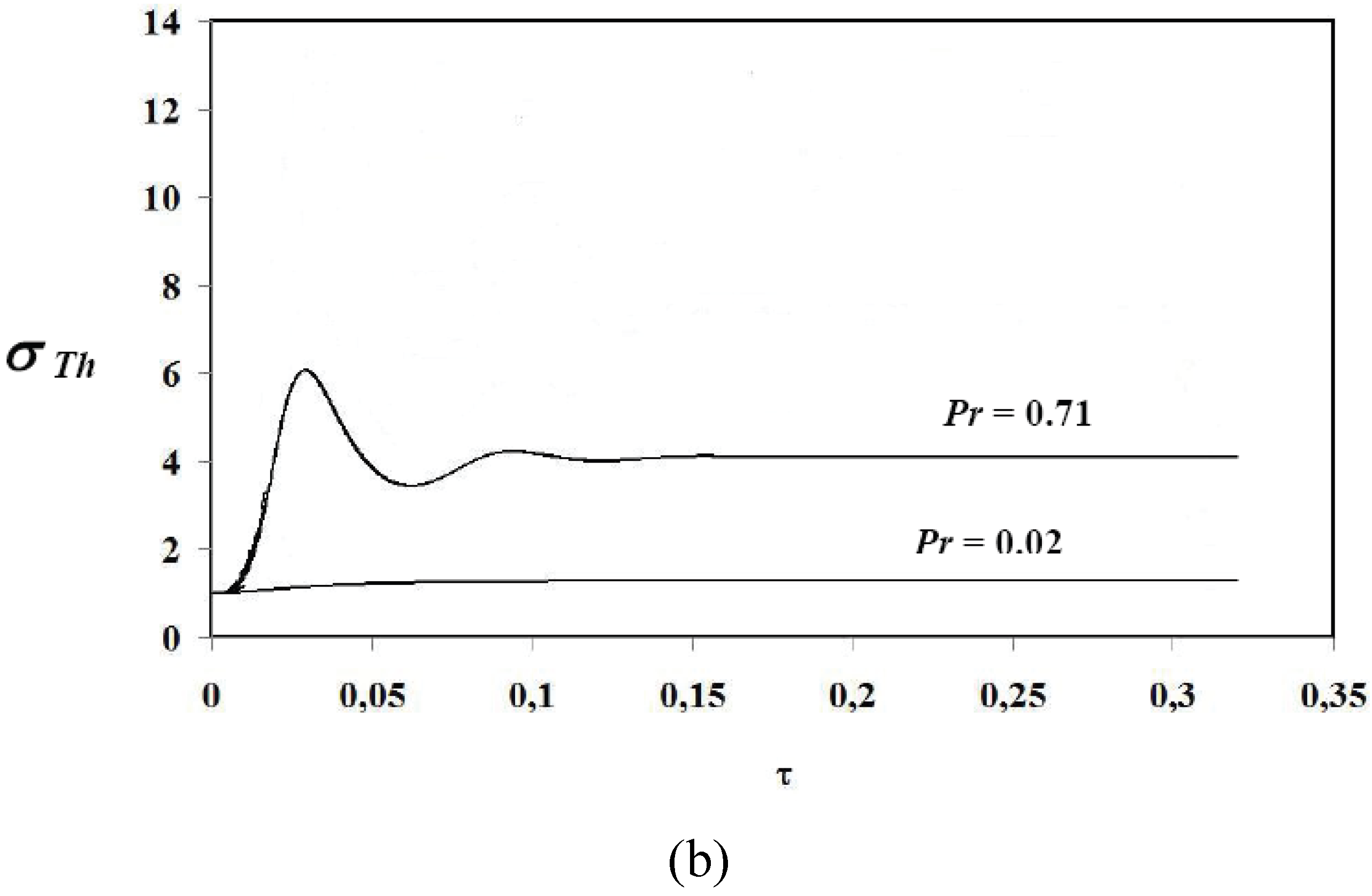
18], where they found that temperature decreases as Prandtl number increases. Further, source term of velocity depends on product of buoyancy and thermal effects as well as magnetic field (see Equation (12)), consequently, velocity gradients increase as thermal Grashof number and temperature increase. Hartmann number has the effect to suppress the fluid velocity and then to reduce the temperature profile. For these reasons, transient entropy generation increases via the increase of viscous irreversibility and is more pronounced for lower Prandtl number value as illustrated in
Figure 7 as an example. Thus, larger inertial effects are obtained for liquid gallium because of its low Prandtl number. Observed asymptotic behaviour of entropy generation at
Pr = 0.02 for both viscous and thermal irreversibilities (
Figure 7a,7b) show that the system evolves in the linear branch of thermodynamics for irreversible processes, the stationary state is sufficiently close to the equilibrium state, as a consequence, entropy generation, quickly reaches a maximum value, then tends towards a constant value. It could be noticed that the magnetic field effect plays the major role in terms of minimizing energy degradation expressed by entropy generation, practically, one should simply choose the appropriate value of the magnetic field (expressed by Hartmann number) to get less degraded energy.
Figure 6.
Hartmann number versus inclination angle of the magnetic field for Pr = 0.71, GrT = 105 and χ1 = 10−3.
Figure 6.
Hartmann number versus inclination angle of the magnetic field for Pr = 0.71, GrT = 105 and χ1 = 10−3.
Figure 7.
Transient entropy generation for GrT = 105, χ1 = 10−3 and Ha = 0: (a) viscous irreversibility, (b) thermal irreversibility.
Figure 7.
Transient entropy generation for GrT = 105, χ1 = 10−3 and Ha = 0: (a) viscous irreversibility, (b) thermal irreversibility.
Since entropy generation exhibits fluctuations for
Pr = 0.71 when
GrT ≥ 10
4, critical thermal Grashof number
versus Hartmann number was studied for fixed values of the inclination angle of the magnetic field and irreversibility coefficient
χ1 (
i.e.,
α = 0° and
χ1 = 10
−3). Curve plotted in
Figure 8 depicts critical values of thermal Grashof number obtained at each Hartmann number value (0 ≤
Ha ≤ 50), thus for
GrT > Gr
c, the stationary regime is far from the equilibrium state.
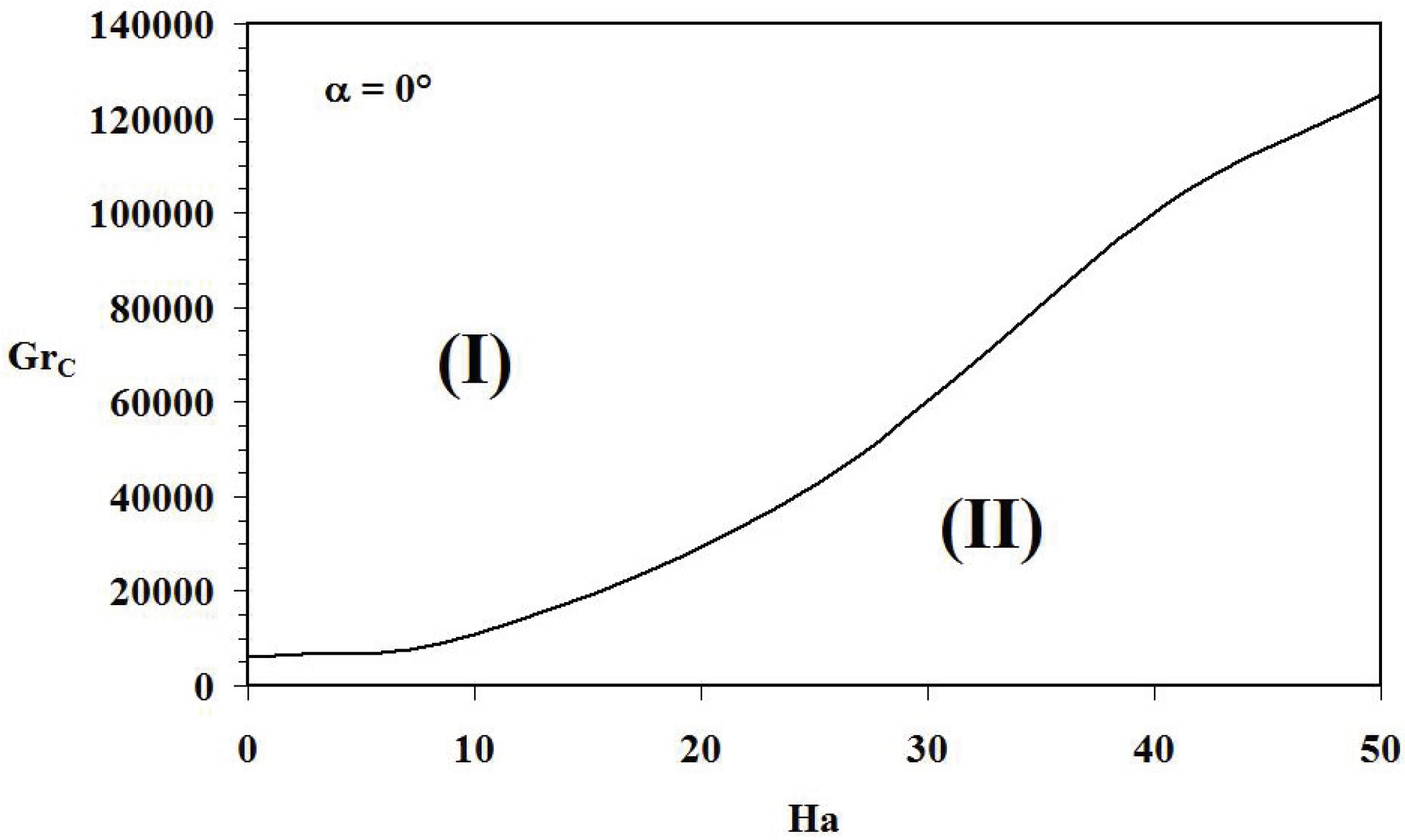
Figure 8 is divided into two regions: (I) represents the region corresponding to higher values of thermal Grashof number for which the system evolves in the non linear branch of thermodynamics of irreversible processes. In this case, entropy generation exhibits oscillatory behaviour corresponding to a non equilibrium state. (II) represents the region corresponding to thermal Grashof number values for which the stationary regime is close to the equilibrium state. In this case, the oscillatory behaviour of entropy generation vanishes and the system evolves in the linear branch of thermodynamics of irreversible processes. It’s important to notice that as Hartmann number value increases, the system tends towards stationary state because critical thermal Grashof number from which the system evolves in non equilibrium state is obtained at higher values. As an illustrative example,
Grc ≈ 10
4 at
Ha = 10 and
Grc ≈ 1.2 × 10
5 at
Ha = 50.
In steady state, magnitude of entropy generation is higher for lower Prandtl number value till
Ha < 25 for
GrT = 10
4 and
Ha > 50 for
GrT = 10
5 (see
Figure 3 and
Figure 4). As mentioned above, for
Pr = 0.02, heat transfer by conduction mode is more pronounced than that for
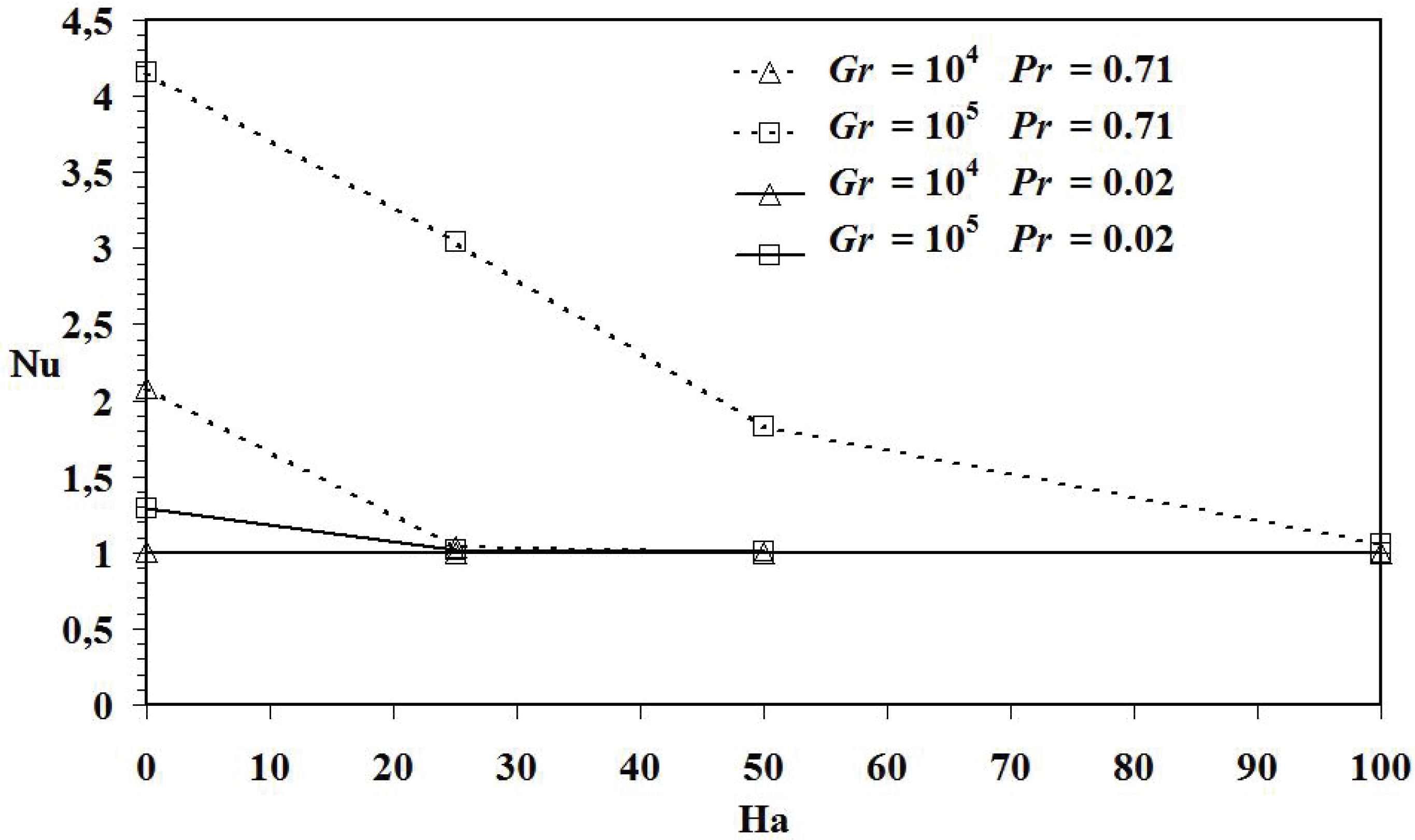
Pr = 0.71. This is proved by the plot of Nusselt number
versus Hartmann number for
GrT = 10
4 and 10
5 as illustrated in
Figure 9. As Hartmann number increases, Nusselt number tends towards unity and then isothermal lines become practically parallel to the active wall and the fluid velocity decreases.
Figure 8.
Critical thermal Grashof number versus Hartmann number for Pr = 0.71, α = 0° and χ1 = 10−3.
Figure 8.
Critical thermal Grashof number versus Hartmann number for Pr = 0.71, α = 0° and χ1 = 10−3.
Figure 9.
Nusselt number versus Hartmann at different thermal Grashof numbers for Pr = 0.71 and 0.02 at α = 0°.
Figure 9.
Nusselt number versus Hartmann at different thermal Grashof numbers for Pr = 0.71 and 0.02 at α = 0°.
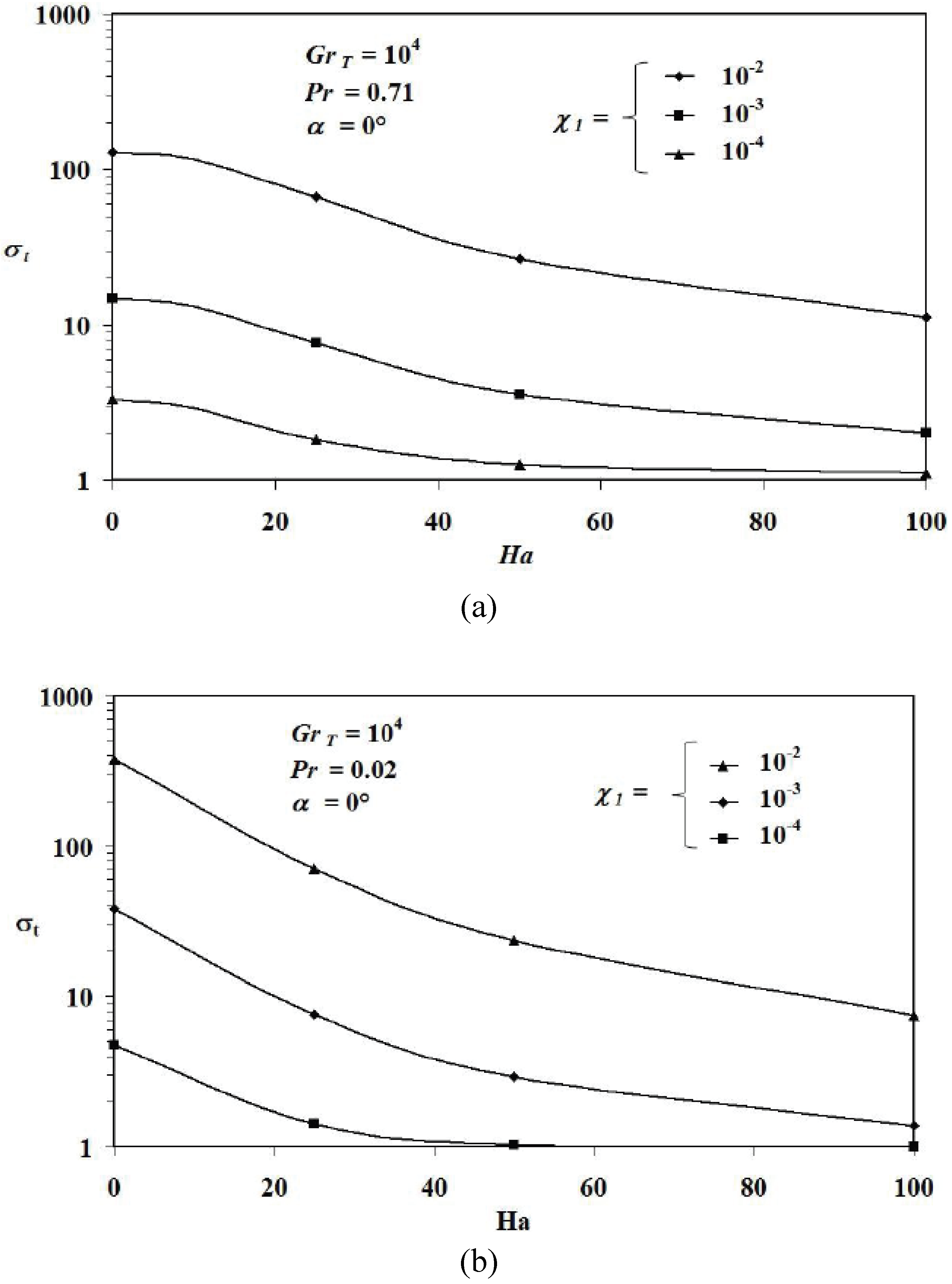
In order to study the influence of the irreversibility coefficient on entropy generation at fixed inclination angle of the magnetic field in steady state,
Figure 10 illustrates the dependence of entropy generation on Hartmann number for
Pr = 0.71 and 0.02 at
GrT = 10
4,
α = 0° and
χ1 = 10
−4, 10
−3 and 10
−2, respectively. As can be seen from
Figure 10, entropy generation decreases as Hartmann number increases, and inversely, it increases with the increase of irreversibility coefficient value. Thus, the presence of the magnetic field (described by Hartmann number), tends to reduce fluid flowing inside the cavity, as Hartmann number increases, the major part of the fluid becomes practically immobile and the flow is simply described by approximately conduction mode for higher values of Hartmann number.
Figure 10.
Total dimensionless entropy generation versus Hartmann number at α = 0°, GrT = 104 at χ1 = 10−2, 10−3, 10−4: (a) Pr = 0.71, (b) Pr = 0.02.
Figure 10.
Total dimensionless entropy generation versus Hartmann number at α = 0°, GrT = 104 at χ1 = 10−2, 10−3, 10−4: (a) Pr = 0.71, (b) Pr = 0.02.
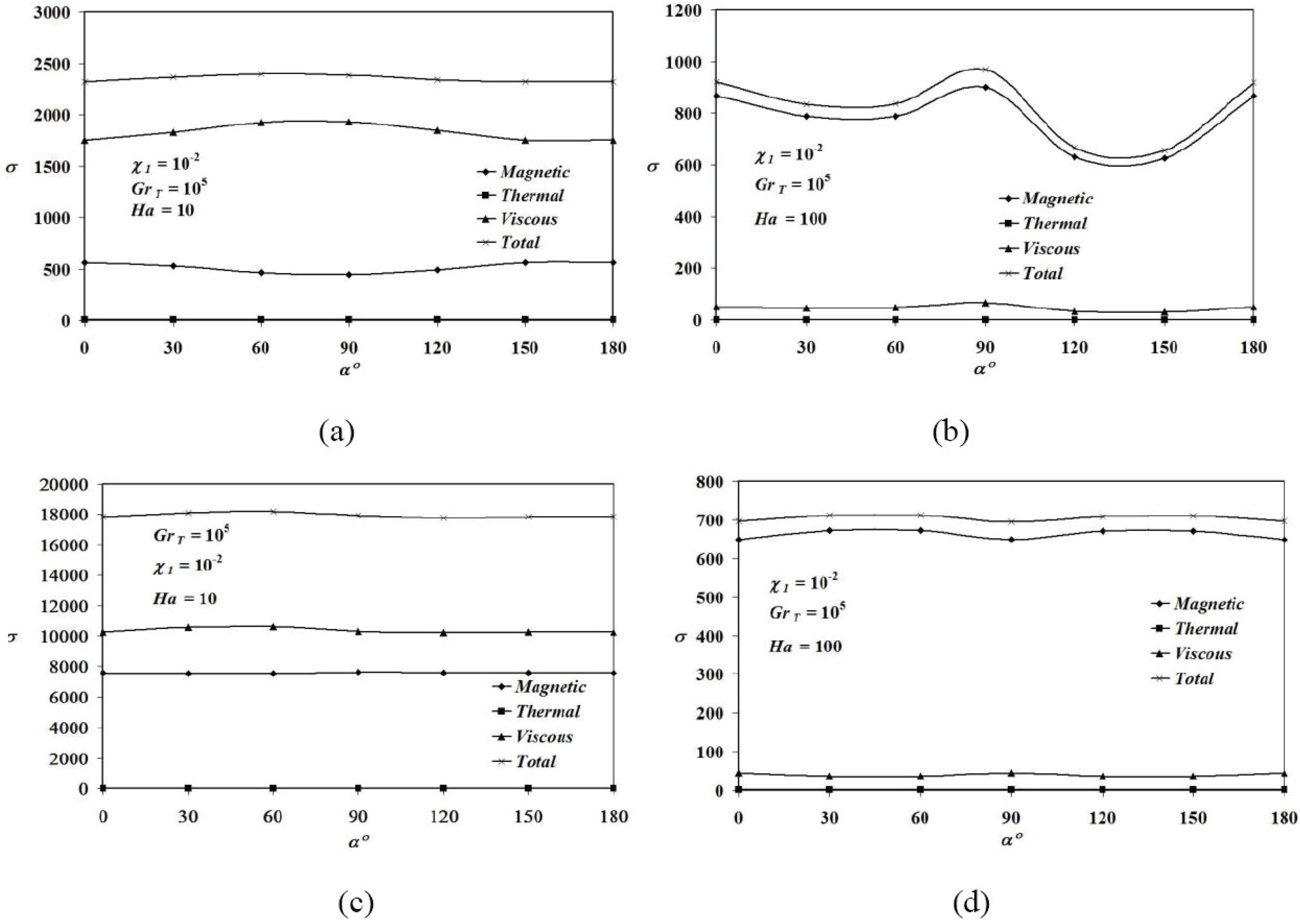
The influence of the inclination angle of the magnetic field on irreversibility due to thermal, viscous and magnetic effects as well as on total entropy generation in stationary state is illustrated in
Figure 11. In this case, values of irreversibility coefficient
χ1 and thermal Grashof number
GrT are fixed and set to be 10
−2 and 10
5, respectively. As can be seen from
Figure 11, the study of irreversibility
versus inclination angle of the magnetic field was performed for lower (respectively higher) Hartmann number. For lower Hartmann number (
Ha = 10),
Figures 11a, 11c show that irreversibility due to fluid friction is the major contribution of total entropy generation.
Figure 11.
Total and local irreversibilities versus α at GrT = 105 and χ1 = 10−2: (a) Pr = 0.71 and Ha = 10, (b) Pr = 0.71 and Ha = 100, (c) Pr = 0.02 and Ha = 10, (d) Pr = 0.02 and Ha = 100.
Figure 11.
Total and local irreversibilities versus α at GrT = 105 and χ1 = 10−2: (a) Pr = 0.71 and Ha = 10, (b) Pr = 0.71 and Ha = 100, (c) Pr = 0.02 and Ha = 10, (d) Pr = 0.02 and Ha = 100.
Entropy generation magnitude for Pr = 0.02 is higher than that for Pr = 0.71. It’s important to notice that maximum values of irreversibility due to viscous effects as well as total entropy generation are obtained at α ≈ 90° and 60° for Pr = 0.71 and 0.02, respectively. Inversely, irreversibility magnitude due to magnetic field is at its minimum value at the same angle for Pr = 0.71, while magnetic irreversibility magnitude slightly decreases as the inclination angle increases for Pr = 0.02. Viscous irreversibility magnitude increases when 0° ≤ α ≤ 90° and 0° ≤ α ≤ 60° for Pr = 0.71 and 0.02, respectively, this behaviour is reversed when 90° < α ≤ 180° and 60° < α ≤ 180° for Pr = 0.71 and 0.02, respectively.
For
Ha = 100 (considerable magnetic field),
Figures 11b, 11d show considerable decrease in magnitude of all irreversibilities as compared to the previous case. Further, entropy generation magnitude for
Pr = 0.02 is less than that for
Pr = 0.71. The effect of the magnetic field is then more pronounced for liquid gallium than for air in terms of fluid velocity deceleration and temperature field decrease. In this case, total entropy generation increases via the increase of irreversibility due to magnetic field. For considerable Hartmann number (
Ha = 100), irreversibility coefficient related to magnetic field is
χ2 =
χ1Ha2 = 10
−2 × 100
2 = 100, further, local irreversibility due to magnetic field is given by
σl,a,Mag =
χ2 (
Usin
a –
Vcos
a)
2, as a consequence total entropy generation is entirely dependent on magnetic irreversibility and convective currents are suppressed. For
Pr = 0.71, Maximum value of irreversibilities due to magnetic field and viscous effects as well as total entropy generation is obtained at
α = 90° (in this case
σl,a,Mag = 100(
U)
2), minimum values of total, magnetic and viscous irreversibilities are obtained at
α ≈ 135°. For
Pr = 0.02 (
Figure 11d), maximum value of total entropy generation as well as that related to magnetic irreversibility is found at
α = 60°. Minimum amplitude of magnetic as well as total irreversibilities is found at
α = 90°, maximum viscous irreversibility is found also at
α = 90°. From the previous figures, irreversibility due to thermal gradients is practically absent, this is due to the fact that the magnetic field induces a quasi equilibrium of isothermal lines through the cavity.
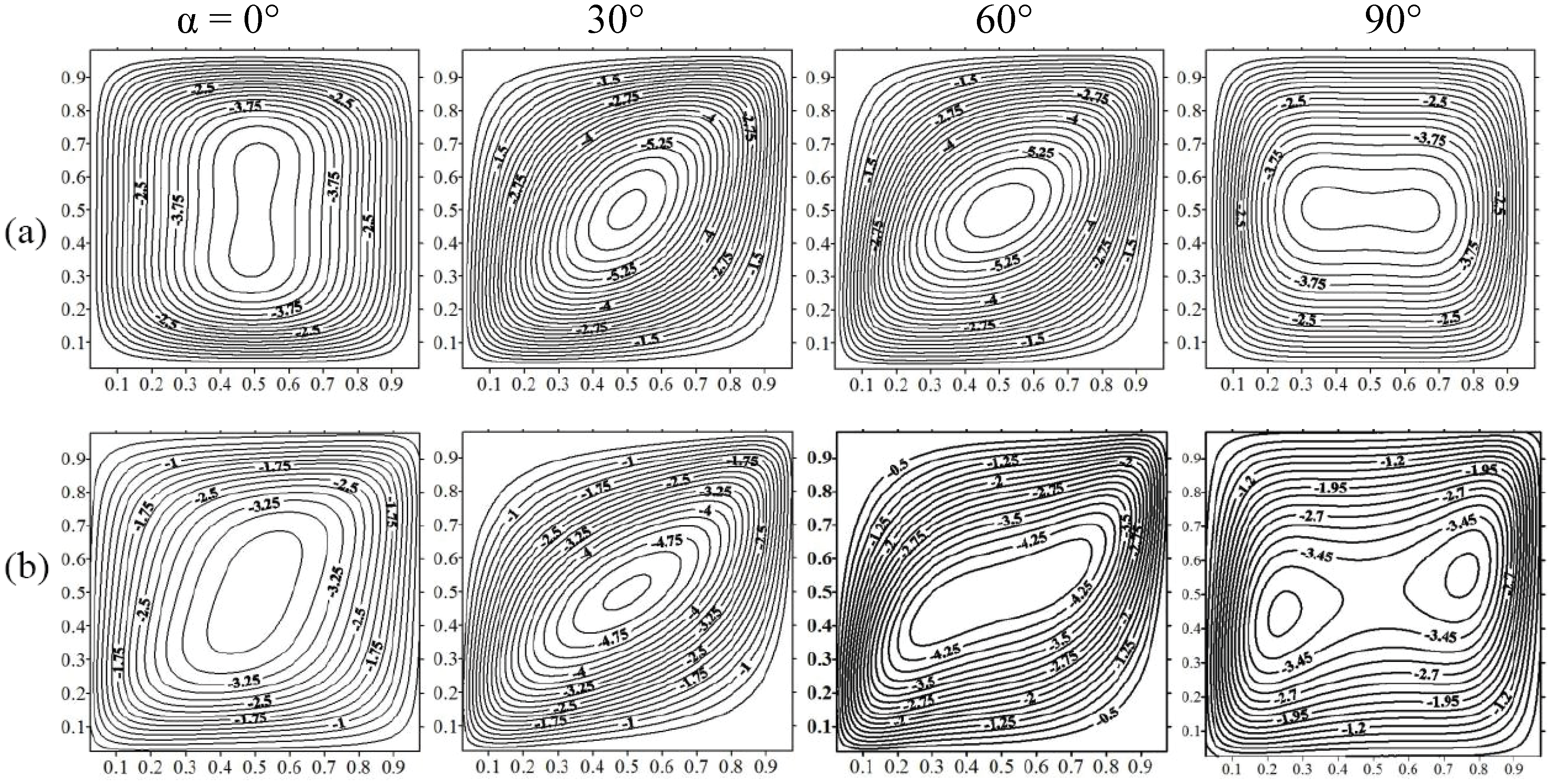
To understand these results, lets plot the streamlines and the isothermal lines for both studied fluids at
GrT = 10
5 in presence of a magnetic field (
Ha = 50) as illustrated in
Figure 12 and
Figure 13. It can be seen from
Figure 12 that, as the direction of the external magnetic field changes from horizontal (
α = 0°) to vertical (
α = 90°), the flow increases up to angle
α = 60° and 30° for
Pr = 0.02 and 0.71, respectively. A higher value of the buoyancy force (
GrT = 10
5) means that the effect of the magnetic field direction is so significant on the flow structure.
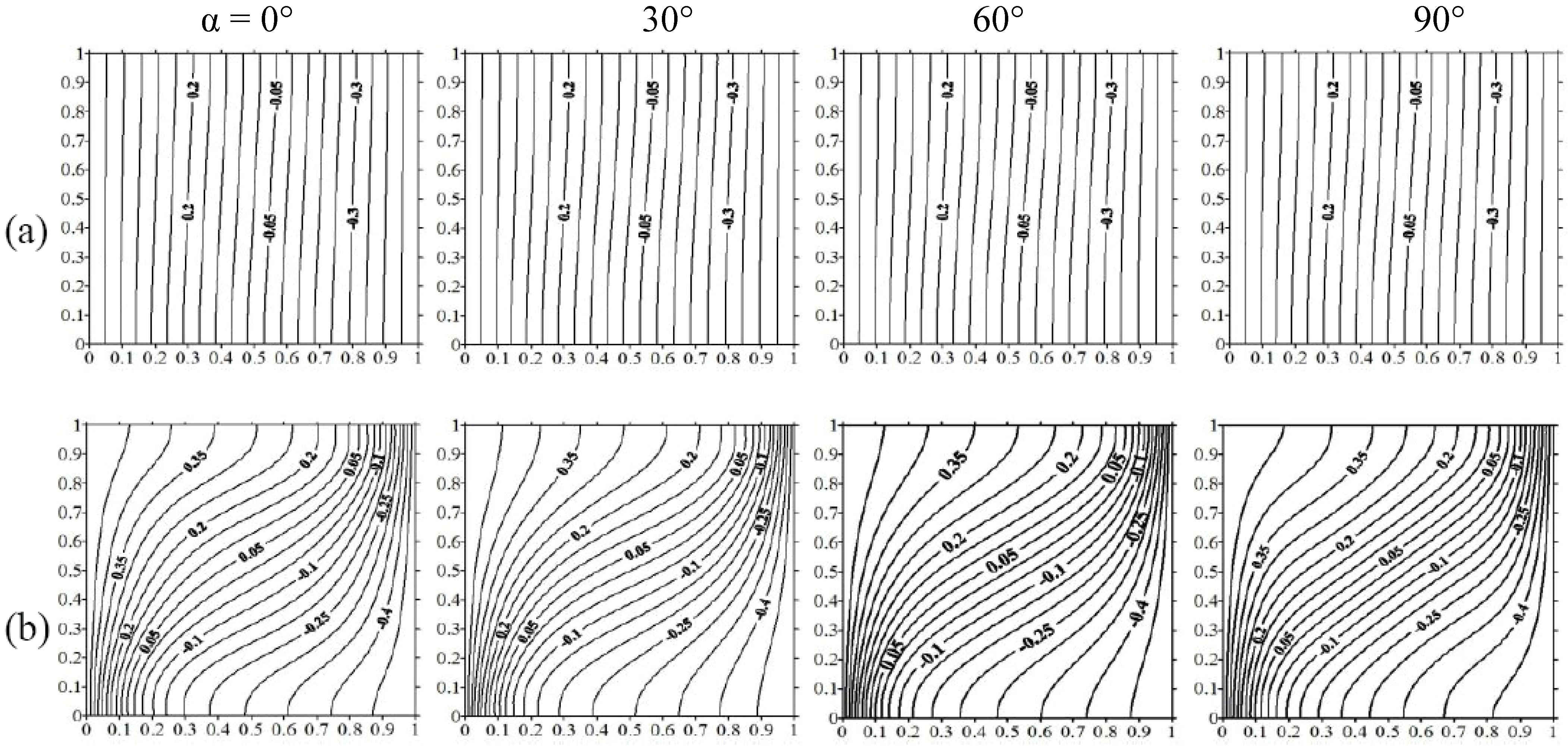
Figure 13 depicts the corresponding isothermal lines. For liquid Gallium (
Pr = 0.02), isothermal lines are practically parallel to the active walls, which means that heat transfer is conduced by conduction mode. For air, thermal boundary layer thickness decreases as the inclination angle increases inducing an increase in heat transfer from horizontal to vertical direction of the magnetic field.
At local level,
Figure 14 shows distribution of entropy generation lines inside the cavity in absence of the magnetic field (
Ha = 0) for 10
3 ≤
GrT ≤ 10
5 at
χ1 = 10
−3. For
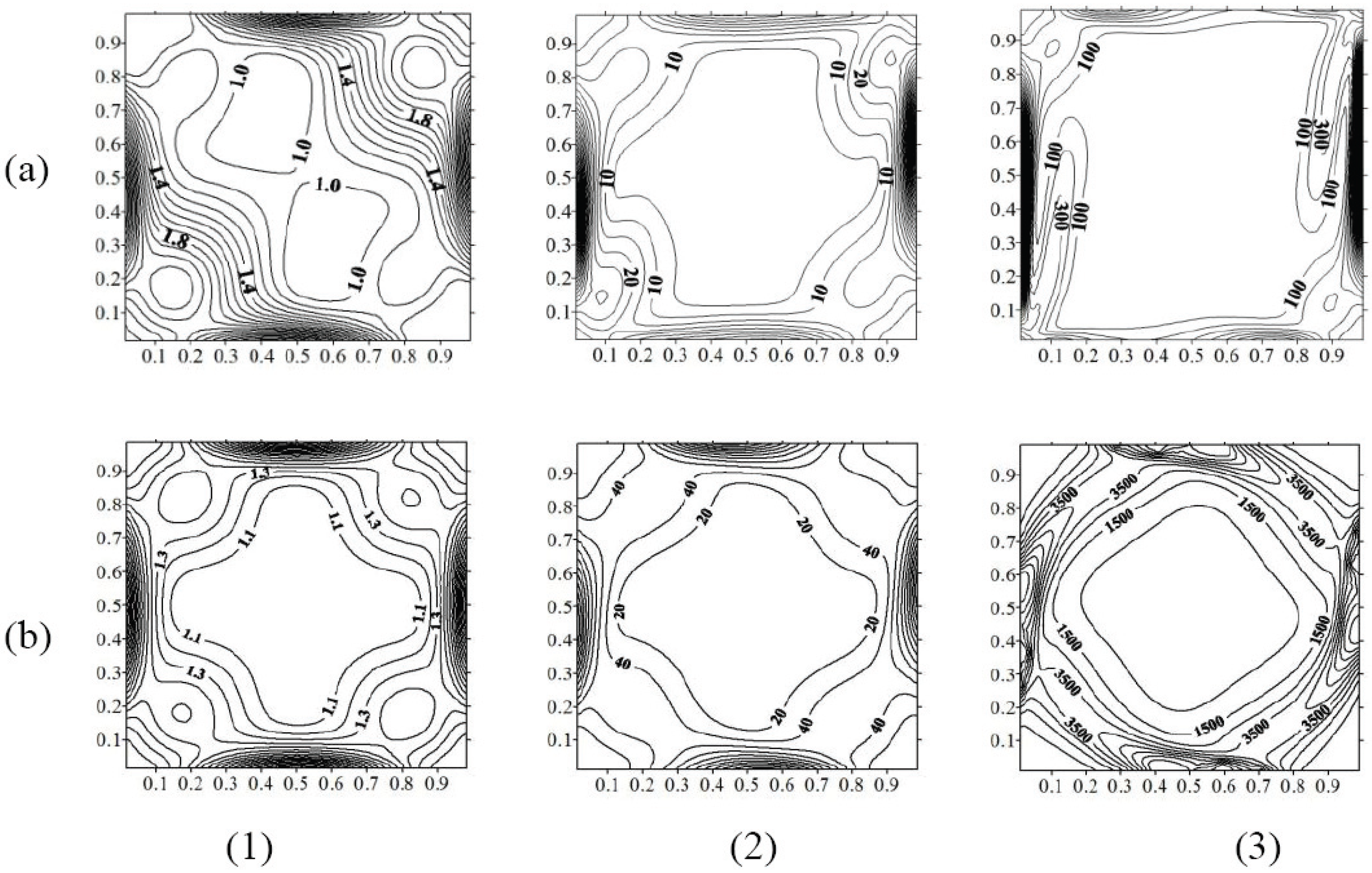
Pr = 0.71, entropy generation lines increase in magnitude with thermal Grashof number and are confined through the active walls (isothermal walls), namely on bottom of the warmed wall and on top of the cooled wall due to the presence of strong thermal and velocity gradients in these regions. For liquid gallium,
Figure 14b shows distribution of irreversibility through the whole cavity except its center. Magnitude of entropy generation lines increases with buoyancy effect. For small Prandtl number value, as thermal Grashof number increases, velocity gradients considerably increase causing the augmentation of local entropy generation. In presence of the magnetic field (
i.e., for
Ha = 50) and for
GrT = 10
5 and
χ1 = 10
−3,
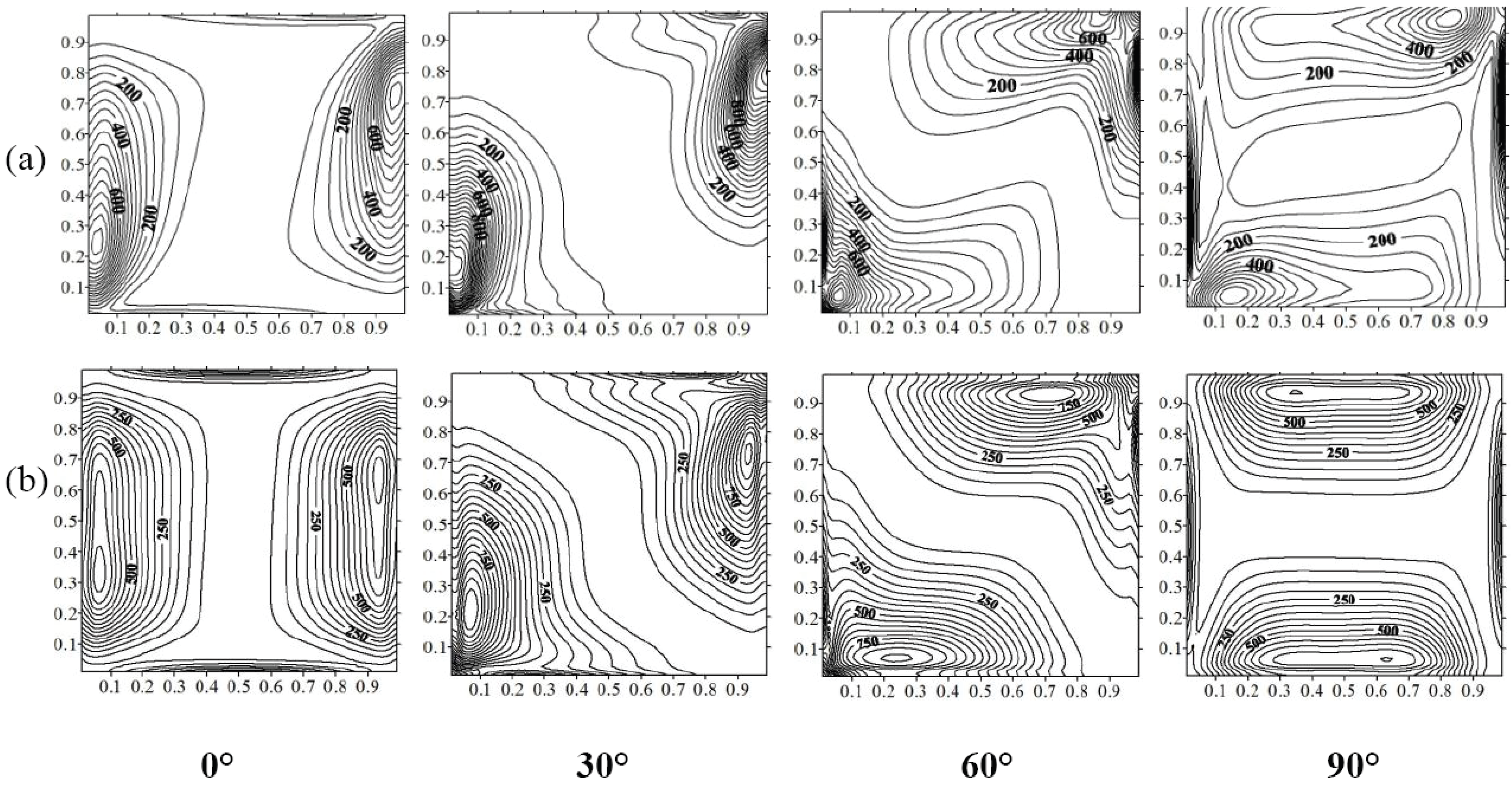
Figure 15 shows the influence of the inclination angle of the magnetic field on entropy generation lines. Entropy generation is lower in magnitude around the center of the cavity. Entropy generates at a higher magnitude near the cavity walls. At
α = 0°, both of the active walls act as strong concentrators of irreversibility due to higher value of magnetic irreversibility as shown above.
As compared to
Figure 14, the presence of a magnetic field reduces the entropy generation amplitude. A significant portion of the cavity extended along the direction of the magnetic field inside the cavity and represents an idle region for entropy production, where entropy generation is practically zero. It can be seen that as the inclination angle increases, entropy generation lines increase in magnitude for both fluids (
α = 30°), then gradually decrease and are distributed on top of cooled and bottom of heated walls as well as on right side of upper and left side of lower adiabatic walls (
α = 60°). Finally at
α = 90°, entropy generation lines are distributed through the entire cavity except its centre for
Pr = 0.71, while irreversibility lines are mainly distributed through the insulated walls for
Pr = 0.02.
Figure 12.
Stream lines at GrT = 105 , Ha = 50 for: (a) Pr = 0.02, (b) Pr = 0.71.
Figure 12.
Stream lines at GrT = 105 , Ha = 50 for: (a) Pr = 0.02, (b) Pr = 0.71.
Figure 13.
Isothermal lines at GrT = 105 , Ha = 50 for: (a) Pr = 0.02, (b) Pr = 0.71.
Figure 13.
Isothermal lines at GrT = 105 , Ha = 50 for: (a) Pr = 0.02, (b) Pr = 0.71.
Figure 14.
Entropy generation maps at Ha = 0 and χ1 = 10−3: (a) Pr = 0.71, (b) Pr = 0.02, (1) GrT = 103, (2) GrT = 104, (3) GrT = 105.
Figure 14.
Entropy generation maps at Ha = 0 and χ1 = 10−3: (a) Pr = 0.71, (b) Pr = 0.02, (1) GrT = 103, (2) GrT = 104, (3) GrT = 105.
Figure 15.
Entropy generation maps at GrT = 105, χ1 = 10−3, Ha = 50: (a) Pr = 0.71, (b) Pr = 0.02.
Figure 15.
Entropy generation maps at GrT = 105, χ1 = 10−3, Ha = 50: (a) Pr = 0.71, (b) Pr = 0.02.