Generalized Alpha-Beta Divergences and Their Application to Robust Nonnegative Matrix Factorization
Abstract
:1. Introduction
1.1. Introduction to NMF and Basic Multiplicative Algorithms for NMF
2. The Alpha-Beta Divergences
2.1. Special Cases of the AB-Divergence
2.2. Properties of AB-Divergence: Duality, Inversion and Scaling
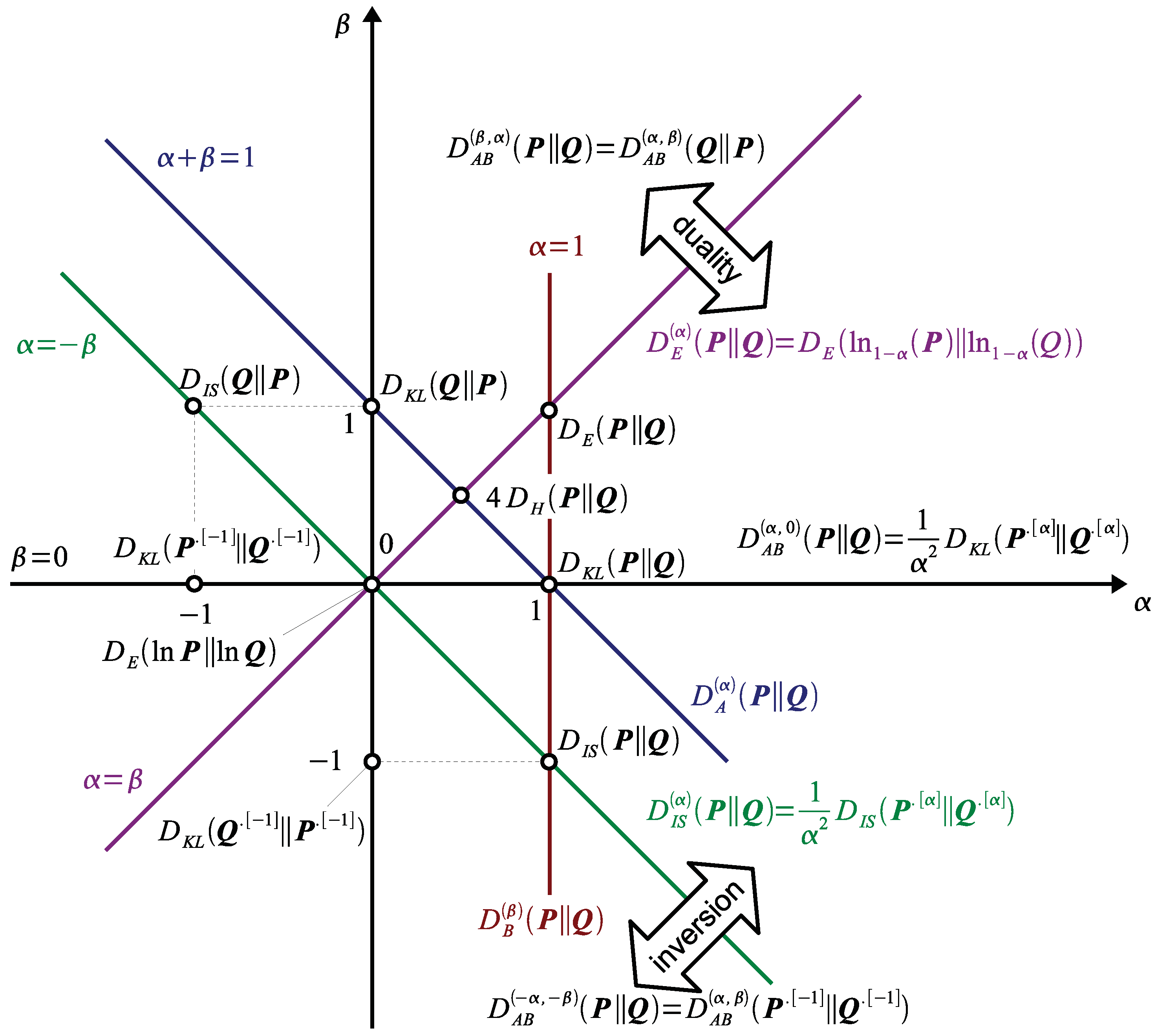
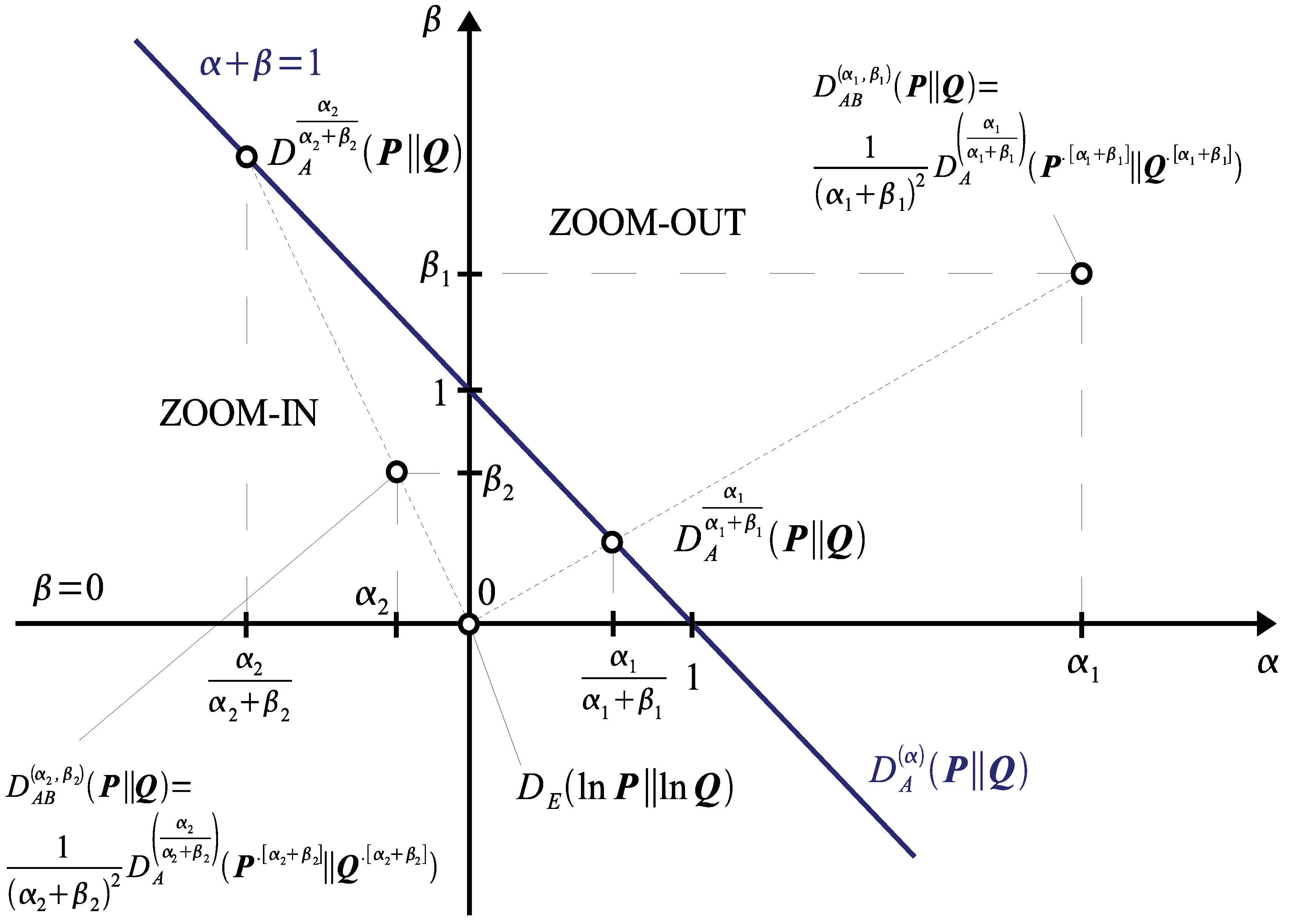
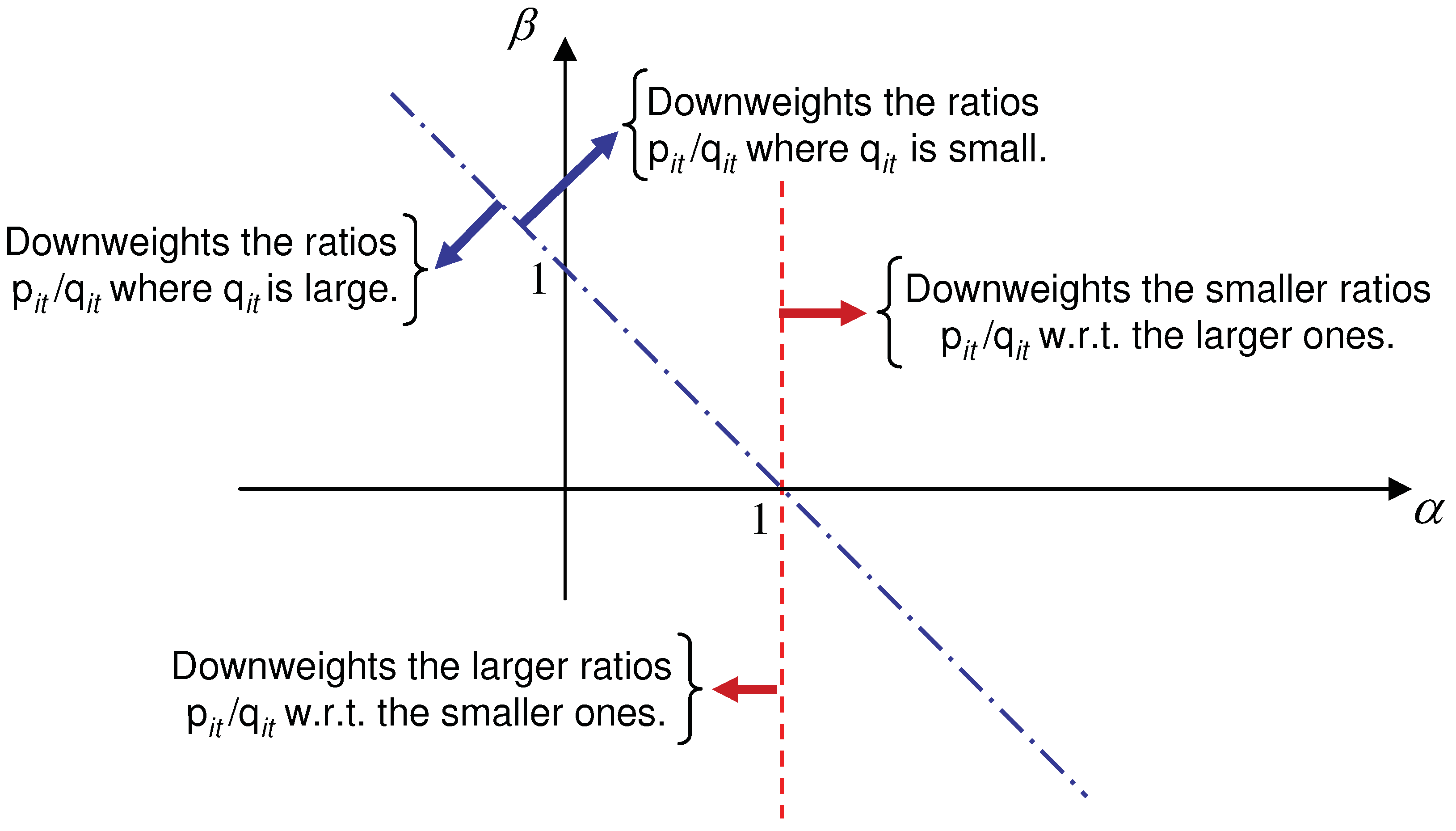
2.3. Why is AB-Divergence Potentially Robust?
3. Generalized Multiplicative Algorithms for NMF
3.1. Derivation of Multiplicative NMF Algorithms Based on the AB-Divergence
3.2. Conditions for a Monotonic Descent of AB-Divergence
3.3. A Conditional Auxiliary Function

3.4. Unconditional Auxiliary Function
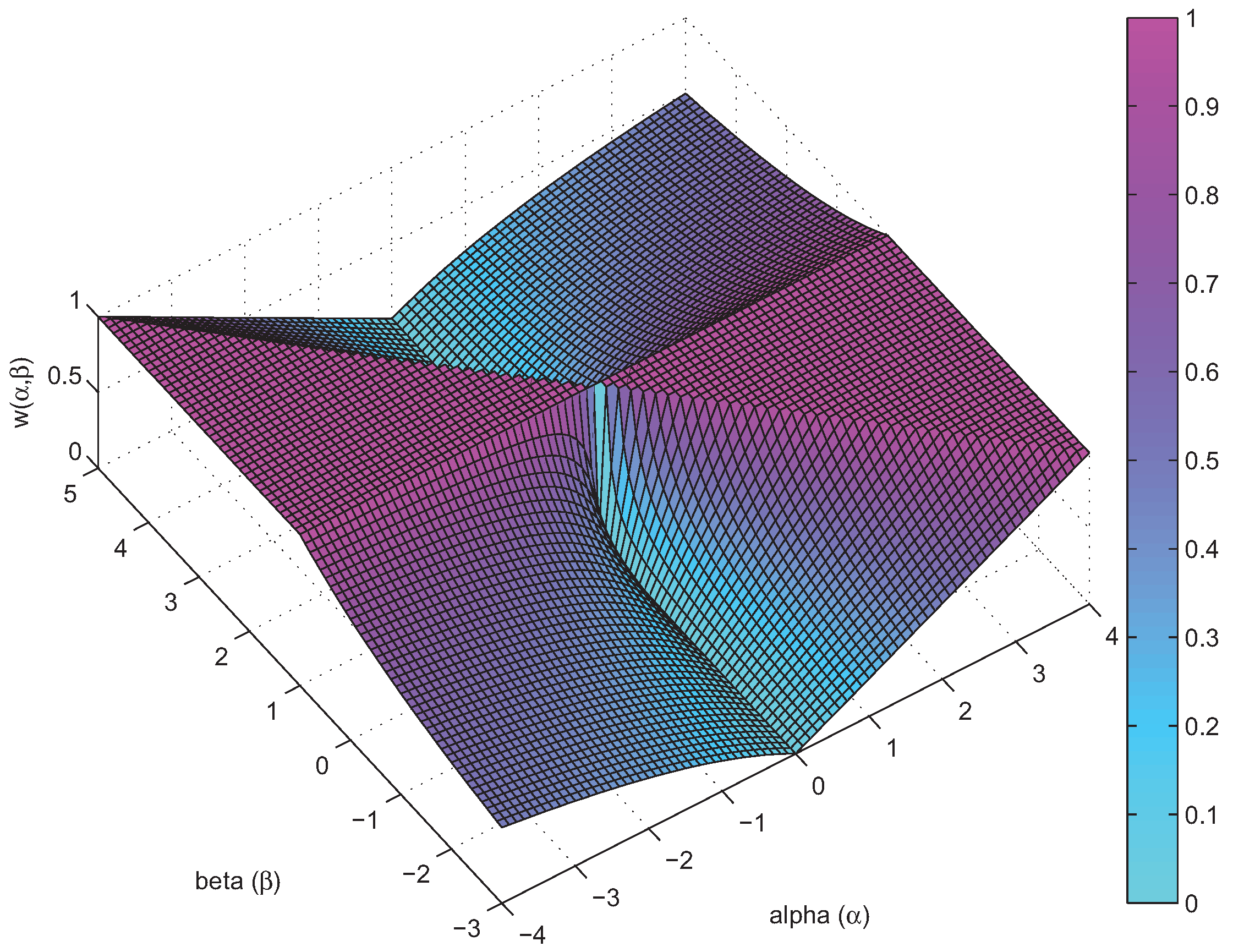
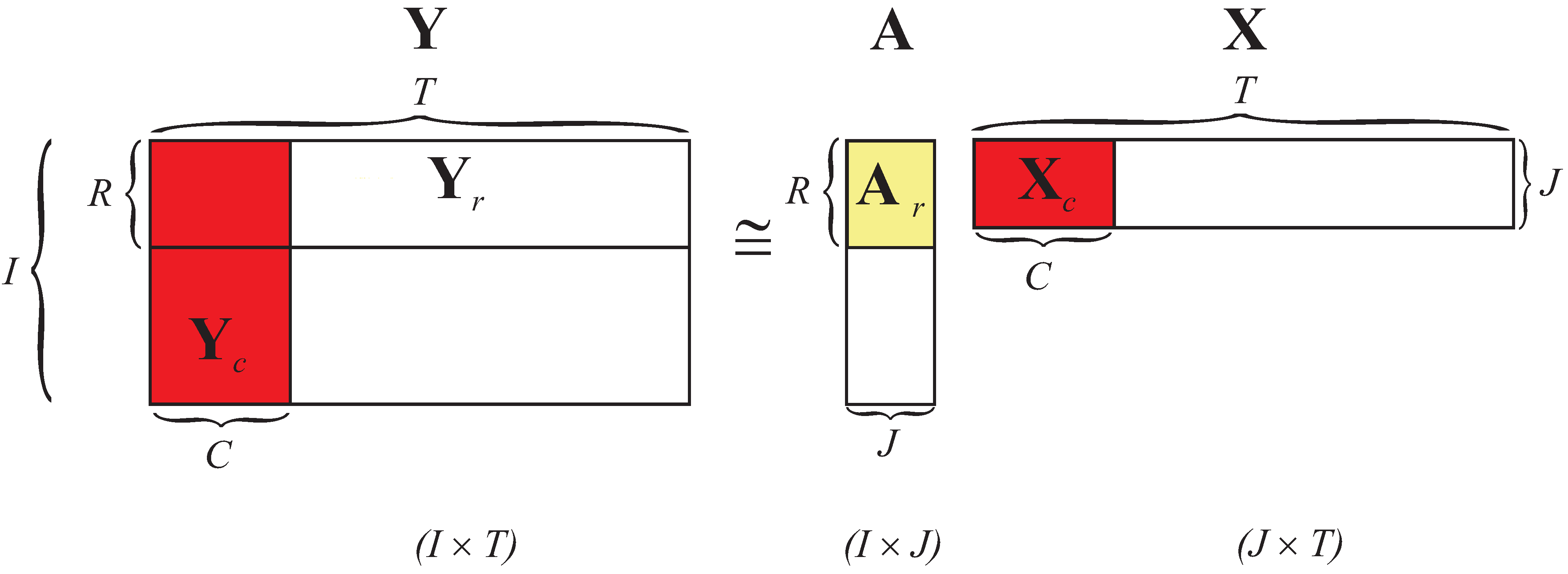
3.5. Multiplicative NMF Algorithms for Large-Scale Low-Rank Approximation
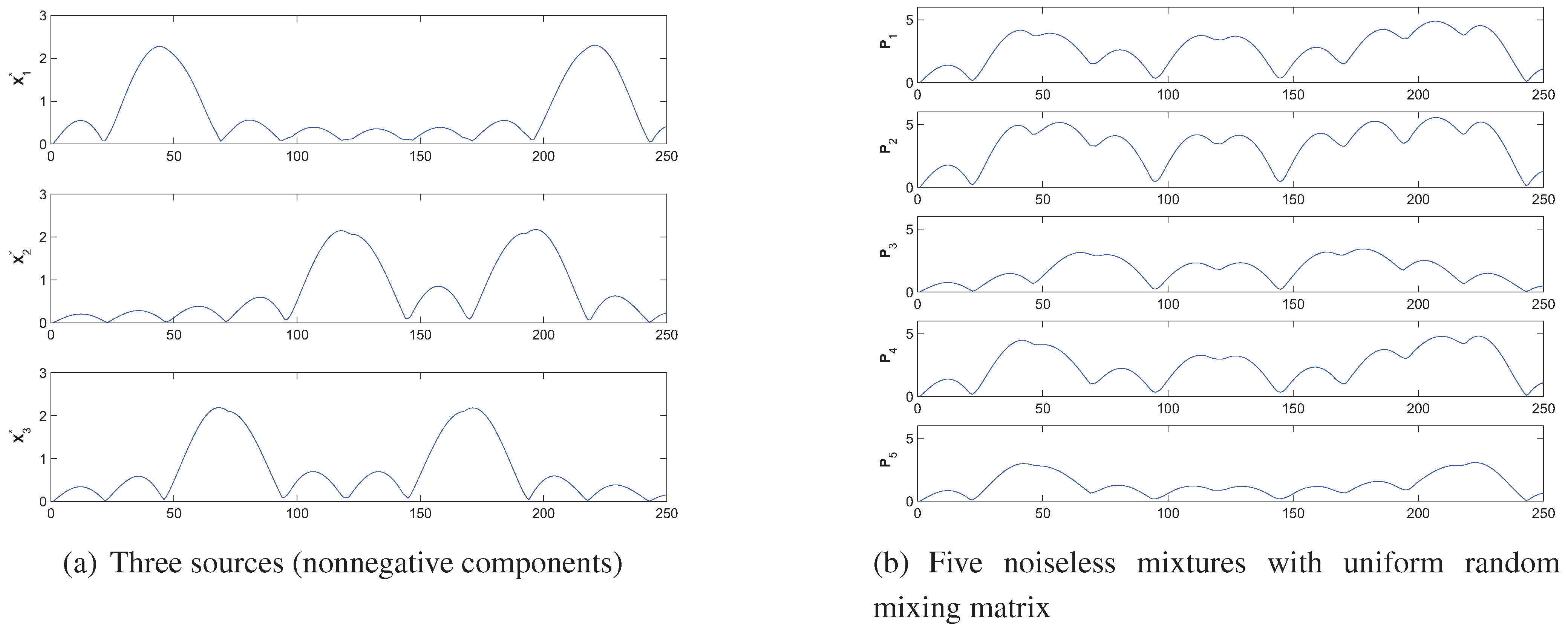
4. Simulations and Experimental Results
- What is approximately a range of parameters alpha and beta for which the AB-multiplicative NMF algorithm exhibits the balance between relatively fastest convergence and good performance.
- What is approximately the range of parameters of alpha and beta for which the AB-multiplicative NMF algorithm provides a stable solution independent of how many iterations are needed.
- How robust is the AB-multiplicative NMF algorithm to noisy mixtures under multiplicative Gaussian noise, additive Gaussian noise, spiky biased noise? In other words, find a reasonable range of parameters for which the AB-multiplicative NMF algorithm gives improved performance when the data are contaminated by the different types of noise.



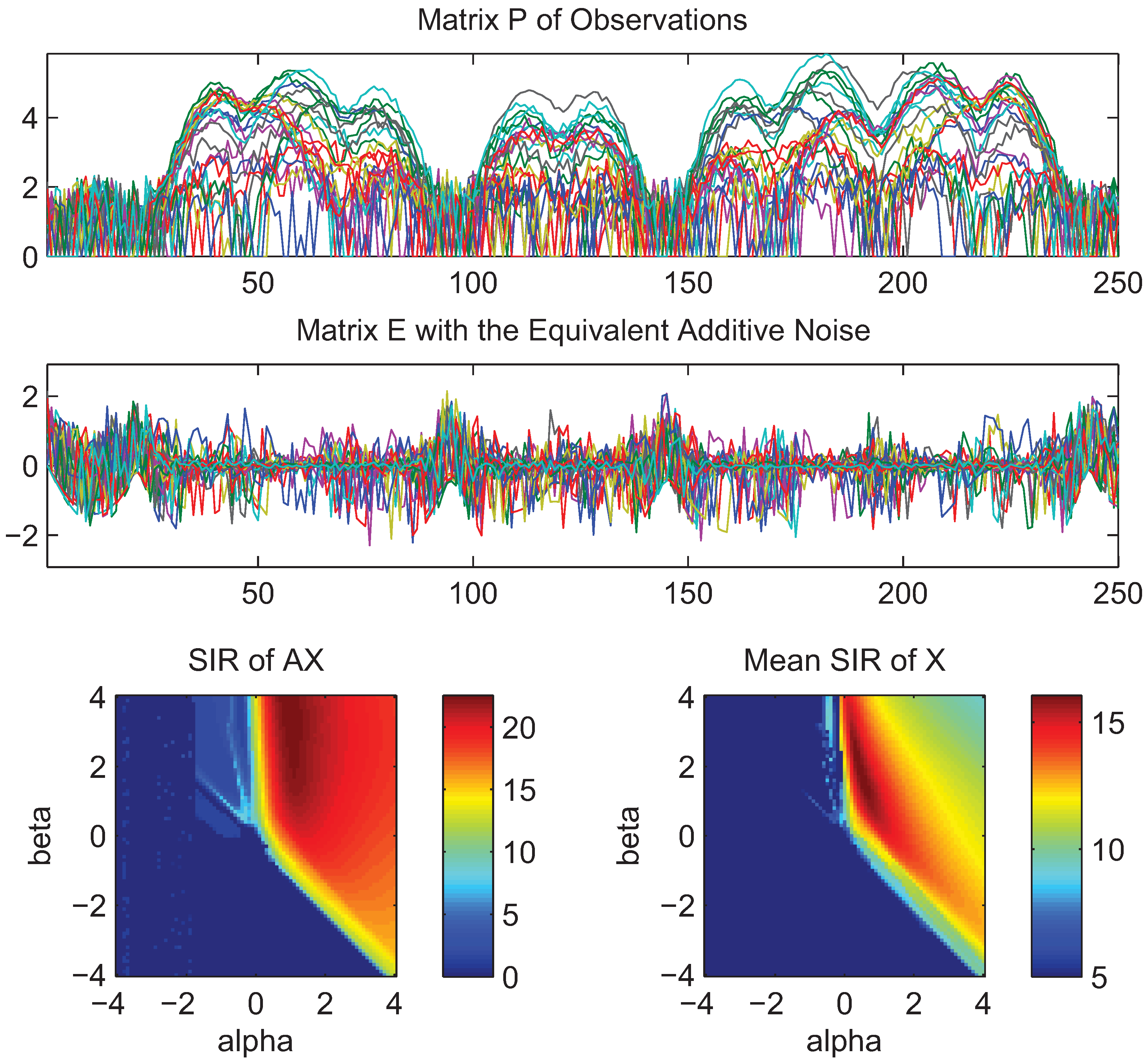
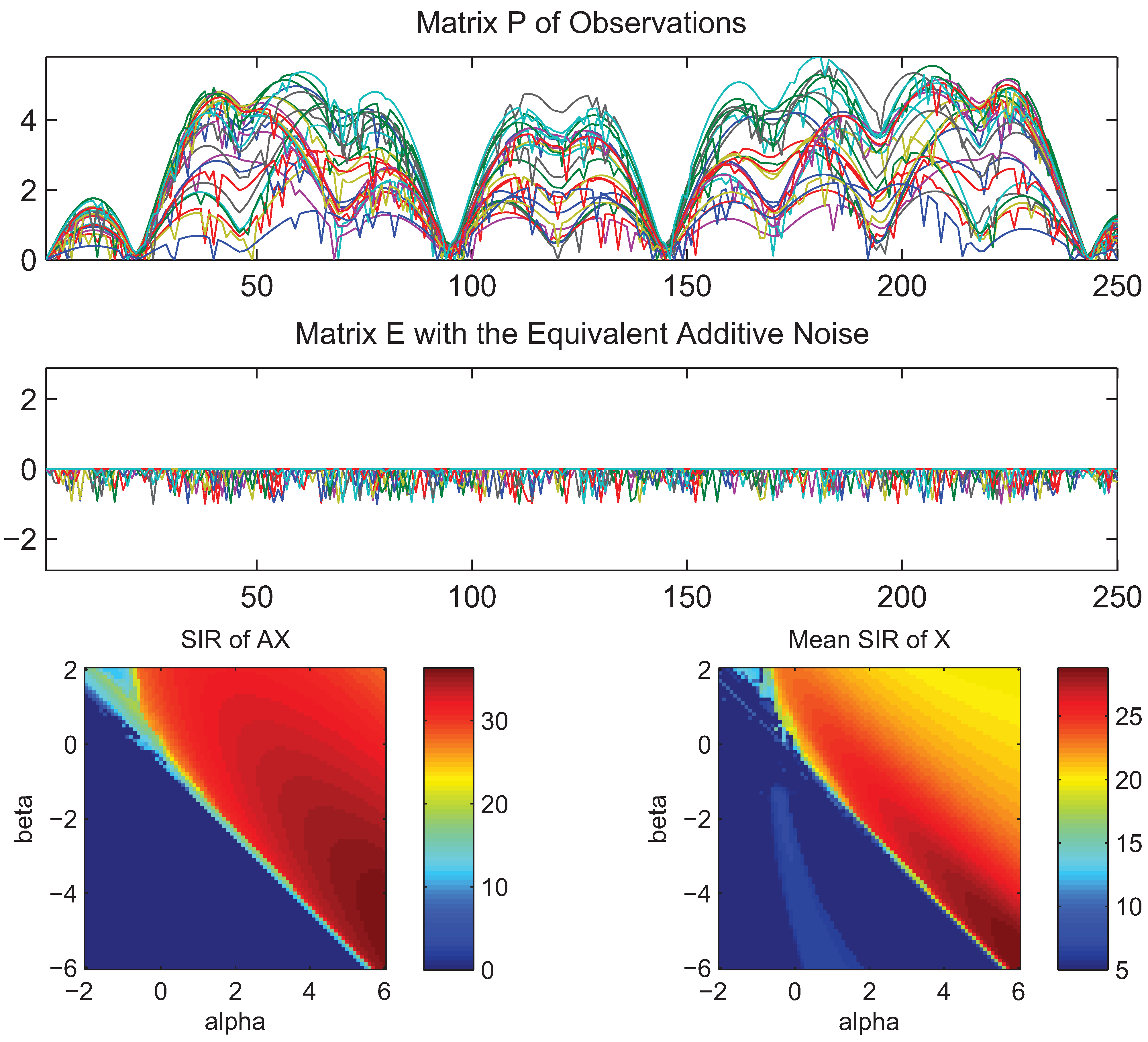
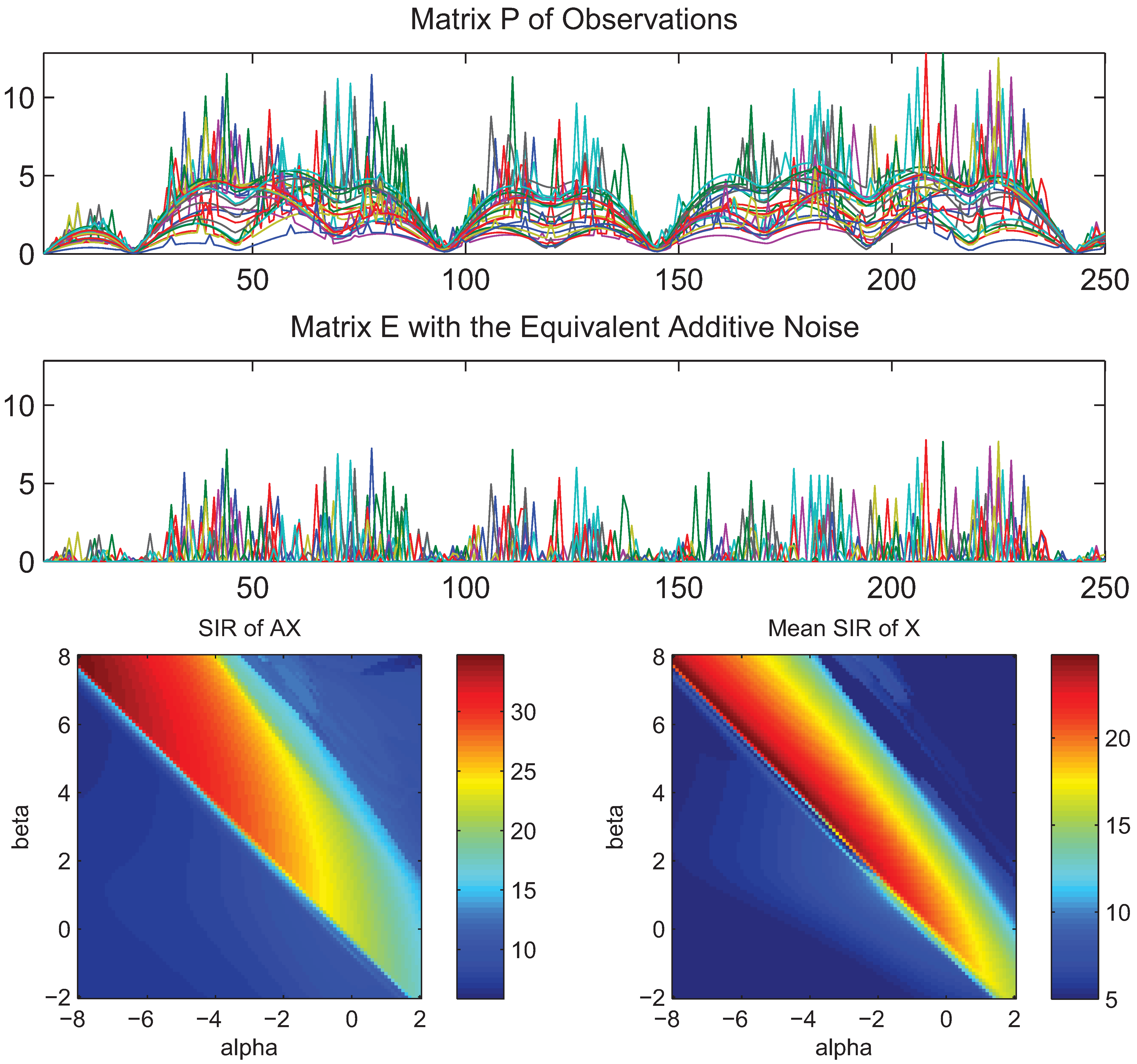
5. Conclusions
References
- Amari, S. Differential-Geometrical Methods in Statistics; Springer Verlag: New York, NY, USA, 1985. [Google Scholar]
- Amari, S. Dualistic geometry of the manifold of higher-order neurons. Neural Network. 1991, 4, 443–451. [Google Scholar] [CrossRef]
- Amari, S.; Nagaoka, H. Methods of Information Geometry; Oxford University Press: New York, NY, USA, 2000. [Google Scholar]
- Amari, S. Integration of stochastic models by minimizing α-divergence. Neural Comput. 2007, 19, 2780–2796. [Google Scholar] [CrossRef] [PubMed]
- Amari, S. Information geometry and its applications: Convex function and dually flat manifold. In Emerging Trends in Visual Computing; Nielsen, F., Ed.; Springer Lecture Notes in Computer Science: Palaiseau, France, 2009a; Volume 5416, pp. 75–102. [Google Scholar]
- Amari, S.; Cichocki, A. Information geometry of divergence functions. Bull. Pol. Acad. Sci. Math. 2010, 58, 183–195. [Google Scholar] [CrossRef]
- Cichocki, A.; Zdunek, R.; Phan, A.H.; Amari, S. Nonnegative Matrix and Tensor Factorizations; John Wiley & Sons Ltd.: Chichester, UK, 2009. [Google Scholar]
- Cichocki, A.; Zdunek, R.; Amari, S. Csiszár’s divergences for nonnegative matrix factorization: Family of new algorithms. In Lecture Notes in Computer Science; Springer: Charleston, SC, USA, 2006; Volume 3889, pp. 32–39. [Google Scholar]
- Kompass, R. A Generalized divergence measure for nonnegative matrix factorization. Neural Comput. 2006, 19, 780–791. [Google Scholar] [CrossRef] [PubMed]
- Dhillon, I.; Sra, S. Generalized nonnegative matrix approximations with Bregman divergences. Neural Inform. Process. Syst. 2005, 283–290. [Google Scholar]
- Amari, S. α-divergence is unique, belonging to both f-divergence and Bregman divergence classes. IEEE Trans. Inform. Theor. 2009b, 55, 4925–4931. [Google Scholar] [CrossRef]
- Murata, N.; Takenouchi, T.; Kanamori, T.; Eguchi, S. Convergence-guaranteed multi U-Boost and Bregman divergence. Neural Comput. 2004, 16, 1437–1481. [Google Scholar] [CrossRef] [PubMed]
- Fujimoto, Y.; Murata, N. A modified EM Algorithm for mixture models based on Bregman divergence. Ann. Inst. Stat. Math. 2007, 59, 57–75. [Google Scholar] [CrossRef]
- Zhu, H.; Rohwer, R. Bayesian invariant measurements of generalization. Neural Process. Lett. 1995, 2, 28–31. [Google Scholar] [CrossRef]
- Zhu, H.; Rohwer, R. Measurements of generalisation based on information geometry. In Mathematics of Neural Networks: Model Algorithms and Applications; Ellacott, S.W., Mason, J.C., Anderson, I.J., Eds.; Kluwer: Norwell, MA, USA, 1997; pp. 394–398. [Google Scholar]
- Nielsen, F.; Nock, R. Sided and symmetrized Bregman centroids. IEEE Trans. Inform. Theor. 2009, 56, 2882–2903. [Google Scholar] [CrossRef]
- Boissonnat, J.D.; Nielsen, F.; Nock, R. Bregman Voronoi diagrams. Discrete Comput. Geom. 2010, 44, 281–307. [Google Scholar] [CrossRef]
- Yamano, T. A generalization of the Kullback-Leibler divergence and its properties. J. Math. Phys. 2009, 50, 85–95. [Google Scholar] [CrossRef]
- Minami, M.; Eguchi, S. Robust blind source separation by Beta-divergence. Neural Comput. 2002, 14, 1859–1886. [Google Scholar]
- Bregman, L. The relaxation method of finding a common point of convex sets and its application to the solution of problems in convex programming. Comp. Math. Phys. USSR 1967, 7, 200–217. [Google Scholar] [CrossRef]
- Csiszár, I. Eine Informations Theoretische Ungleichung und ihre Anwendung auf den Beweiss der Ergodizität von Markoffschen Ketten. Magyar Tud. Akad. Mat. Kutató Int. Közl 1963, 8, 85–108. [Google Scholar]
- Csiszár, I. Axiomatic characterizations of information measures. Entropy 2008, 10, 261–273. [Google Scholar] [CrossRef]
- Csiszár, I. Information measures: A critial survey. In Proceedings of the Transactions of the 7th Prague Conference, Prague, Czechoslovakia, 18–23 August 1974; pp. 83–86.
- Ali, M.; Silvey, S. A general class of coefficients of divergence of one distribution from another. J. Roy. Stat. Soc. 1966, Ser B, 131–142. [Google Scholar]
- Hein, M.; Bousquet, O. Hilbertian metrics and positive definite kernels on probability measures. In Proceedings of the Tenth International Workshop on Artificial Intelligence and Statistics, Barbados, 6–8 January 2005; pp. 136–143.
- Zhang, J. Divergence function, duality, and convex analysis. Neural Comput. 2004, 16, 159–195. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Matsuzoe, H. Dualistic differential geometry associated with a convex function. In Springer Series of Advances in Mechanics and Mathematics; 2008; Springer: New York, NY, USA; pp. 58–67. [Google Scholar]
- Lafferty, J. Additive models, boosting, and inference for generalized divergences. In Proceedings of the Twelfth Annual Conference on Computational Learning Theory (COLT’99), Santa Cruz, CA, USA, 7-9 July 1999.
- Banerjee, A.; Merugu, S.; Dhillon, I.S.; Ghosh, J. Clustering with Bregman divergences. J. Mach. Learn. Res. 2005, 6, 1705–1749. [Google Scholar]
- Villmann, T.; Haase, S. Divergence based vector quantization using Fréchet derivatives. Neural Comput. 2011, in press. [Google Scholar]
- Villmann, T.; Haase, S.; Schleif, F.M.; Hammer, B. Divergence based online learning in vector quantization. In Proceedings of the International Conference on Artifial Intelligence and Soft Computing (ICAISC’2010), LNAI, Zakopane, Poland, 13–17 June 2010.
- Cichocki, A.; Amari, S.; Zdunek, R.; Kompass, R.; Hori, G.; He, Z. Extended SMART algorithms for nonnegative matrix factorization. In Lecture Notes in Artificial Intelligence; Springer: Zakopane, Poland, 2006; Volume 4029, pp. 548–562. [Google Scholar]
- Cichocki, A.; Zdunek, R.; Choi, S.; Plemmons, R.; Amari, S. Nonnegative tensor factorization using Alpha and Beta divergences. In IEEE International Conference on Acoustics, Speech, and Signal Processing, Honolulu, Hawaii, USA, 15–20 April 2007; Volume III, pp. 1393–1396.
- Cichocki, A.; Zdunek, R.; Choi, S.; Plemmons, R.; Amari, S.I. Novel multi-layer nonnegative tensor factorization with sparsity constraints. In Lecture Notes in Computer Science; Springer: Warsaw, Poland, 2007; Volume 4432, pp. 271–280. [Google Scholar]
- Cichocki, A.; Amari, S. Families of Alpha- Beta- and Gamma- divergences: Flexible and robust measures of similarities. Entropy 2010, 12, 1532–1568. [Google Scholar] [CrossRef]
- Paatero, P.; Tapper, U. Positive matrix factorization: A nonnegative factor model with optimal utilization of error estimates of data values. Environmetrics 1994, 5, 111–126. [Google Scholar] [CrossRef]
- Lee, D.; Seung, H. Learning of the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [PubMed]
- Lee, D.; Seung, H. Algorithms for Nonnegative Matrix Factorization; MIT Press: Cambridge MA, USA, 2001; Volume 13, pp. 556–562. [Google Scholar]
- Gillis, N.; Glineur, F. Nonnegative factorization and maximum edge biclique problem. ECORE discussion paper 2010. 106 (also CORE DP 2010/59). Available online: http://www.ecore.be/DPs/dp_1288012410.pdf (accessed on 1 November 2008).
- Daube-Witherspoon, M.; Muehllehner, G. An iterative image space reconstruction algorthm suitable for volume ECT. IEEE Trans. Med. Imag. 1986, 5, 61–66. [Google Scholar] [CrossRef] [PubMed]
- De Pierro, A. On the relation between the ISRA and the EM algorithm for positron emission tomography. IEEE Trans. Med. Imag. 1993, 12, 328–333. [Google Scholar] [CrossRef] [PubMed]
- De Pierro, A.R. A Modified expectation maximization algorithm for penalized likelihood estimation in emission tomography. IEEE Trans. Med. Imag. 1995, 14, 132–137. [Google Scholar] [CrossRef] [PubMed]
- De Pierro, A.; Yamagishi, M.B. Fast iterative methods applied to tomography models with general Gibbs priors. In Proceedings of the SPIE Technical Conference on Mathematical Modeling, Bayesian Estimation and Inverse Problems, Denver, CO, USA, 21 July 1999; Volume 3816, pp. 134–138.
- Lantéri, H.; Roche, M.; Aime, C. Penalized maximum likelihood image restoration with positivity constraints: multiplicative algorithms. Inverse Probl. 2002, 18, 1397–1419. [Google Scholar] [CrossRef]
- Byrne, C. Accelerating the EMML algorithm and related iterative algorithms by rescaled block-iterative (RBI) methods. IEEE Trans. Med. Imag. 1998, IP-7, 100–109. [Google Scholar] [CrossRef] [PubMed]
- Lewitt, R.; Muehllehner, G. Accelerated iterative reconstruction for positron emission tomography based on the EM algorithm for maximum-likelihood estimation. IEEE Trans. Med. Imag. 1986, MI-5, 16–22. [Google Scholar] [CrossRef] [PubMed]
- Byrne, C. Signal Processing: A Mathematical Approach; A.K. Peters, Publ.: Wellesley, MA, USA, 2005. [Google Scholar]
- Shepp, L.; Vardi, Y. Maximum likelihood reconstruction for emission tomography. IEEE Trans. Med. Imag. 1982, MI-1, 113–122. [Google Scholar] [CrossRef] [PubMed]
- Kaufman, L. Maximum likelihood, least squares, and penalized least squares for PET. IEEE Trans. Med. Imag. 1993, 12, 200–214. [Google Scholar] [CrossRef] [PubMed]
- Lantéri, H.; Soummmer, R.; Aime, C. Comparison between ISRA and RLA algorithms: Use of a Wiener filter based stopping criterion. Astron. Astrophys. Suppl. 1999, 140, 235–246. [Google Scholar] [CrossRef]
- Cichocki, A.; Zdunek, R.; Amari, S.I. Hierarchical ALS algorithms for nonnegative matrix and 3D tensor factorization. In Lecture Notes on Computer Science; Springer: London, UK, 2007; Volume 4666, pp. 169–176. [Google Scholar]
- Minka, T. Divergence measures and message passing. In Microsoft Research Technical Report; MSR-TR-2005-173; Microsoft Research Ltd.: Cambridge, UK, 7 December 2005. [Google Scholar]
- Févotte, C.; Bertin, N.; Durrieu, J.L. Nonnegative matrix factorization with the Itakura-Saito divergence with application to music analysis. Neural Comput. 2009, 21, 793–830. [Google Scholar] [CrossRef] [PubMed]
- Itakura, F.; Saito, F. Analysis synthesis telephony based on the maximum likelihood method. In Proceedings of the 6th International Congress on Acoustics, Tokyo, Japan, 21–28 August 1968; pp. 17–20.
- Basu, A.; Harris, I.R.; Hjort, N.; Jones, M. Robust and efficient estimation by minimising a density power divergence. Biometrika 1998, 85, 549–559. [Google Scholar] [CrossRef]
- Jones, M.; Hjort, N.; Harris, I.R.; Basu, A. A comparison of related density-based minimum divergence estimators. Biometrika 1998, 85, 865–873. [Google Scholar] [CrossRef]
- Kivinen, J.; Warmuth, M. Exponentiated gradient versus gradient descent for linear predictors. Inform. Comput. 1997, 132, 1–63. [Google Scholar] [CrossRef]
- Cichocki, A.; Lee, H.; Kim, Y.D.; Choi, S. Nonnegative matrix factorization with α-divergence. Pattern Recogn. Lett. 2008, 29, 1433–1440. [Google Scholar] [CrossRef]
- Févotte, C.; Idier, J. Algorithms for nonnegative matrix factorization with the β-divergence. Technical Report arXiv 2010. Available online: http://arxiv.org/abs/1010.1763 (accessed on 13 October 2010).
- Nakano, M.; Kameoka, H.; Le Roux, J.; Kitano, Y.; Ono, N.; Sagayama, S. Convergence-guaranteed multiplicative algorithms for non-negative matrix factorization with β-divergence. In Proceedings of the 2010 IEEE International Workshop on Machine Learning for Signal Processing (MLSP), Kittila, Finland, 29 August–1 September 2010; pp. 283–288.
- Badeau, R.; Bertin, N.; Vincent, E. Stability analysis of multiplicative updates algorithms and application to nonnegative matirx factroization. IEEE Trans. Neural Network. 2010, 21, 1869–1881. [Google Scholar] [CrossRef] [PubMed]
- Favati, P.; Lotti, G.; Menchi, O.; Romani, F. Performance analysis of maximum likelihood methods for regularization problems with nonnegativity constraints. Inverse Probl. 2010, 28, 85013–85030. [Google Scholar] [CrossRef]
- Benvenuto, F.; Zanella, R.; Zanni, L.; Bertero, M. Nonnegative least-squares image deblurring: Improved gradient projection approaches. Inverse Probl. 2010, 26, 25004–25021. [Google Scholar] [CrossRef]
Appendix
A. Non-negativity of the AB-divergence
B. Proof of the Conditional Auxiliary Function Character of
C. Necessary and Sufficient Conditions for Convexity
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/.)
Share and Cite
Cichocki, A.; Cruces, S.; Amari, S.-i. Generalized Alpha-Beta Divergences and Their Application to Robust Nonnegative Matrix Factorization. Entropy 2011, 13, 134-170. https://doi.org/10.3390/e13010134
Cichocki A, Cruces S, Amari S-i. Generalized Alpha-Beta Divergences and Their Application to Robust Nonnegative Matrix Factorization. Entropy. 2011; 13(1):134-170. https://doi.org/10.3390/e13010134
Chicago/Turabian StyleCichocki, Andrzej, Sergio Cruces, and Shun-ichi Amari. 2011. "Generalized Alpha-Beta Divergences and Their Application to Robust Nonnegative Matrix Factorization" Entropy 13, no. 1: 134-170. https://doi.org/10.3390/e13010134




