A Maximum Entropy Modelling of the Rain Drop Size Distribution
Abstract
:1. Introduction
2. Data
2.1. Synthetic Data
| Category | μ | Size (Number drops) | ||
|---|---|---|---|---|
| Very Light | 1.7 | 4.7 | 0.0 , 0.1 , 0.5 | 50, 100, 200, 500 |
| Moderate | 2.9 | 4.7 | 0.0 , 0.1 , 0.3, 0.5 | 50, 100, 200, 500 |
| Heavy | 3.9 | 5.2 | 0.0 , 0.1 , 0.3, 0.5 | 50, 100, 200, 500 |
| Very Heavy | 6.1 | 6.3 | 0.0 , 0.1 , 0.5 | 50, 100, 200, 500 |
2.2. Experimental
3. Methods
3.1. Method of Moments
3.2. Maximum Likelihood Estimation
3.3. Maximum Entropy Principle
3.4. Performance Measures
4. Results
4.1. Analysis of Synthetic Data

| Scenario | Methods of Modelling | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rain Category | Size | MLE | MM234 | MaxEnt-3 | MaxEnt-4 | MaxEnt-6 | MaxEnt-8 | |||||
| Moderate | 0.0 | 50 | 0 | 0 | (10) | 0 | (22) | 1 | (35) | 6 | (45) | (*)43 (50) |
| 100 | 1 | 0 | (7) | 0 | (17) | 1 | (24) | 9 | (39) | 39 (50) | ||
| 200 | 3 | 0 | (5) | 1 | (11) | 4 | (21) | 11 | (32) | 31 (50) | ||
| 500 | 3 | 0 | (6) | 0 | (4) | 0 | (11) | 11 | (36) | 36 (50) | ||
| 0.1 | 50 | 1 | 0 | (5) | 1 | (17) | 1 | (24) | 8 | (41) | 39 (50) | |
| 100 | 1 | 0 | (4) | 1 | (12) | 3 | (31) | 12 | (43) | 33 (50) | ||
| 200 | 3 | 0 | (3) | 0 | (6) | 1 | (19) | 7 | (33) | 39 (50) | ||
| 500 | 7 | 0 | (1) | 0 | (4) | 4 | (15) | 2 | (25) | 37 (50) | ||
| 0.3 | 100 | 1 | 0 | (16) | 0 | (3) | 1 | (23) | 4 | (40) | 44 (50) | |
| 0.5 | 50 | 0 | 1 | (25) | 0 | (0) | 1 | (31) | 14 | (48) | (*)34 (50) | |
| 100 | 0 | 0 | (35) | 0 | (1) | 0 | (36) | 7 | (46) | (*)42 (50) | ||
| 200 | 0 | 0 | (37) | 0 | (0) | 0 | (29) | 3 | (46) | 47 (50) | ||
| 500 | 0 | 0 | (45) | 0 | (0) | 0 | (32) | 0 | (48) | 50 (50) | ||



| Scenario | Method | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Rain Category | Size | ||||||||
| Very Heavy | 0.1 | 100 | MLE | - | 0.033 | 0.122 | 0.260 | 0.418 | 0.571 |
| MM234 | 0.088 | 0.105 | 0.109 | 0.117 | 0.125 | 0.123 | |||
| MaxEnt-4 | - | - | - | - | 0.004 | 0.018 | |||
| MaxEnt-6 | - | - | - | - | - | - | |||
| Moderate | 0.0 | 500 | MLE | - | 0.013 | 0.050 | 0.109 | 0.180 | 0.250 |
| MM234 | 0.048 | 0.057 | 0.057 | 0.057 | 0.054 | 0.041 | |||
| MaxEnt-4 | - | - | - | - | 0.011 | 0.045 | |||
| MaxEnt-6 | - | - | - | - | - | - | |||
| Moderate | 0.5 | 50 | MLE | - | 0.037 | 0.133 | 0.271 | 0.415 | 0.539 |
| MM234 | 0.052 | 0.055 | 0.055 | 0.055 | 0.034 | 0.035 | |||
| MaxEnt-4 | - | - | - | - | 0.003 | 0.012 | |||
| MaxEnt-6 | - | - | - | - | - | - | |||
| Very Light | 0.5 | 200 | MLE | - | 0.053 | 0.208 | 0.457 | 0.744 | 1.012 |
| MM234 | 0.230 | 0.283 | 0.283 | 0.283 | 0.289 | 0.281 | |||
| MaxEnt-4 | - | - | - | - | 0.008 | 0.035 | |||
| MaxEnt-6 | - | - | - | - | - | - | |||
| Scenario | Method | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Rain Category | Size | ||||||||
| Very Heavy | 0.1 | 100 | MLE | 0.023 | 0.048 | 0.076 | 0.105 | 0.135 | 0.166 |
| MM234 | 0.065 | 0.027 | 0.091 | 0.282 | 0.544 | 0.880 | |||
| MaxEnt-4 | 0.023 | 0.083 | 0.212 | 0.425 | 0.713 | 1.047 | |||
| MaxEnt-6 | 0.023 | 0.083 | 0.212 | 0.425 | 0.719 | 1.075 | |||
| Moderate | 0.0 | 500 | MLE | 0.016 | 0.050 | 0.097 | 0.150 | 0.208 | 0.269 |
| MM234 | 0.063 | 0.093 | 0.103 | 0.099 | 0.085 | 0.062 | |||
| MaxEnt-4 | 0.016 | 0.038 | 0.048 | 0.044 | 0.041 | 0.066 | |||
| MaxEnt-6 | 0.016 | 0.038 | 0.048 | 0.044 | 0.031 | 0.022 | |||
| Moderate | 0.5 | 50 | MLE | 0.032 | 0.147 | 0.436 | 0.749 | 1.034 | 1.268 |
| MM234 | 0.020 | 0.164 | 0.372 | 0.600 | 0.821 | 1.021 | |||
| MaxEnt-4 | 0.032 | 0.113 | 0.326 | 0.562 | 0.804 | 1.041 | |||
| MaxEnt-6 | 0.032 | 0.113 | 0.326 | 0.562 | 0.802 | 1.036 | |||
| Very Light | 0.5 | 200 | MLE | 0.937 | 1.514 | 1.655 | 1.432 | 0.978 | 0.428 |
| MM234 | 0.599 | 1.098 | 1.502 | 1.818 | 2.056 | 2.225 | |||
| MaxEnt-4 | 0.937 | 1.608 | 2.079 | 2.448 | 2.723 | 2.829 | |||
| MaxEnt-6 | 0.937 | 1.608 | 2.079 | 2.448 | 2.742 | 2.914 | |||
4.2. Analysis of Experimental Measurements

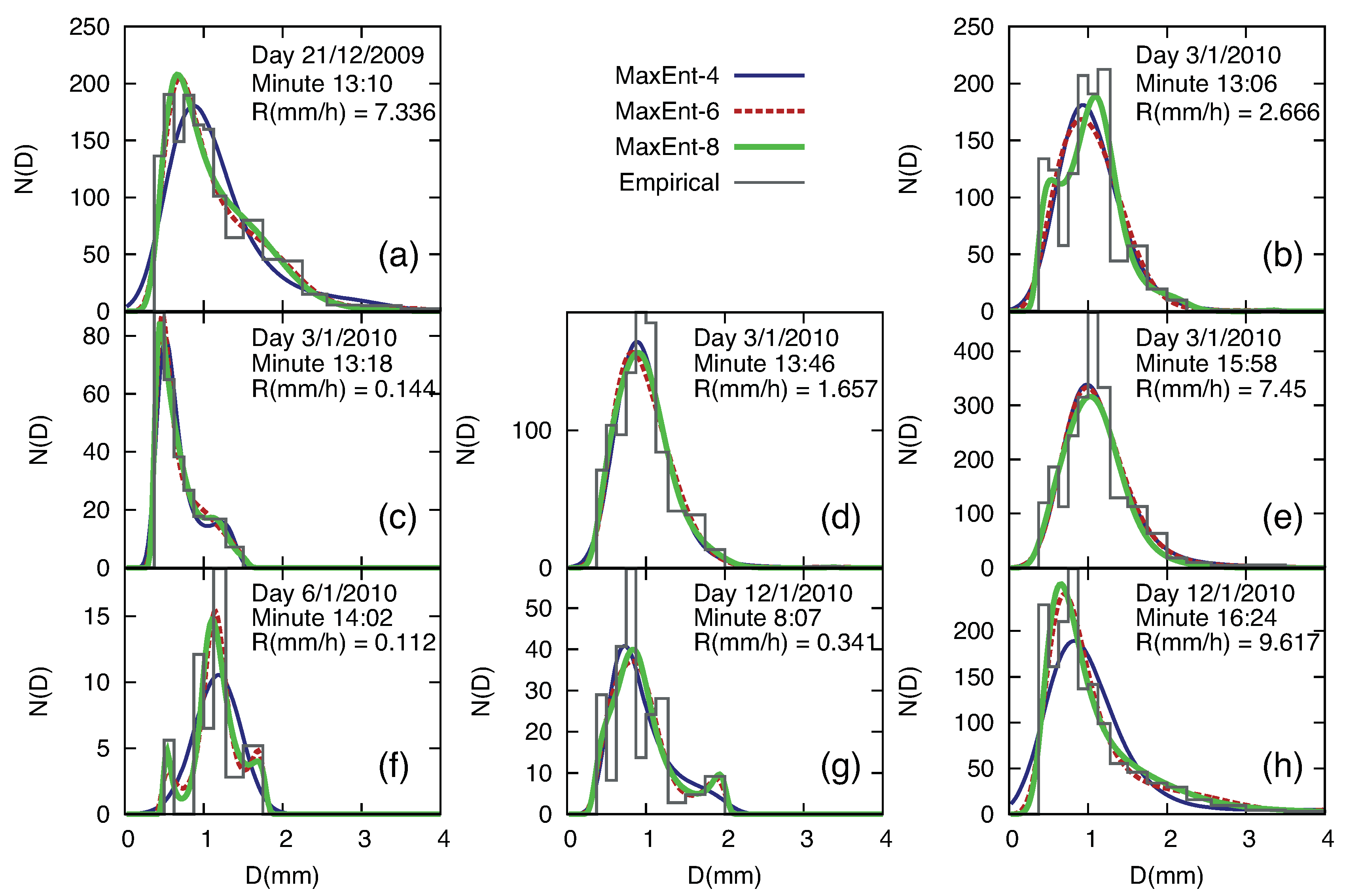


5. Discussion
6. Conclusions
Acknowledgments
References and Notes
- Rosenfeld, D.; Lohmann, U.; Raga, G.B.; O’Dowd, C.D.; Kulmala, M.; Fuzzi, S.; Reissell, A.; Andreae, M.O. Flood or Drought: How Do Aerosols Affect Precipitation? Science 2008, 321, 1309. [Google Scholar] [CrossRef] [PubMed]
- Tokay, A.; Kruger, A.; Krajewski, W.F. Comparison of Drop Size Distribution Measurements by Impact and Optical Disdrometers. J. Appl. Meteor. 1996, 40, 2083–2097. [Google Scholar] [CrossRef]
- Krajewski, W.F.; Kruger, A.; Caracciolo, C.; Golé, R.; Barthes, L.; Creutin, J.D.; Delahaye, J.Y.; Nikolopoulus, E.I.; Odgen, F.; Vison, J.P. DEVEX-disdrometer evaluation experiment: Basic results and implications for hydrological studies. Adv. Water Res. 2006, 26, 311–325. [Google Scholar] [CrossRef]
- Marshall, J.S.; Palmer, W.M.K. The distribution of raindrops with size. J. Meteor. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Feingold, G.; Levin, Z. The log-normal fit to raindrop spectra from frontal convective clouds in Israel. J. Appl. Meteor. 1986, 25, 1346–1363. [Google Scholar] [CrossRef]
- Feingold, G.; Levin, Z. The log-normal size distribution of raindrops: Application to differential reflectivity measurements of rainfall (ZDR). J. Atmos. Oceanic Technol. 1987, 4, 377–382. [Google Scholar] [CrossRef]
- Ulbrich, C.W. Natural variations in the analytical form of the raindrop size distribution. J. Climate Appl. Meteor. 1983, 22, 1764–1775. [Google Scholar] [CrossRef]
- Sauvageot, H.; Koffi, M. Multimodal Raindrop Size Distributions. J. Atmos. Sci. 2000, 57, 2480–2492. [Google Scholar] [CrossRef]
- Radhakrishna, B.; Narayana, T.R. Statistical Characteristics of Multipeak Raindrop Size Distributions at the Surface and Aloft in Different Rain Regimes. Mon. Wea. Rev. 2009, 137, 3501–3518. [Google Scholar] [CrossRef]
- Cao, Q.; Zhang, G. Errors in Estimating Raindrop Size Distribution Parameters Employing Disdrometer and Simulated Raindrop Spectra. J. Appl. Meteor. Climatol. 2009, 48, 406–425. [Google Scholar] [CrossRef]
- Sempere-Torres, D.; Porrá, J.M.; Creutin, J.M. Experimental evidence of a general description for raindrop size distribution properties. J. Geophys. Res. 1998, 103, 1785–1797. [Google Scholar] [CrossRef]
- Lee, G.; Zawadzki, I.; Szyrmer, W.; Sempere-Torres, D.; Uilenhoet, R. A General Approach to Double-Moment Normalization of Drop Size Distributions. J. Appl. Meteor. 2004, 43, 264–281. [Google Scholar] [CrossRef]
- Testud, J.; Oury, S.; Black, R.A.; Amayenc, P.; Dou, X. The Concept of “Normalized" Distribution to Describe Raindrop Spectra: A Tool for Cloud Physics and Cloud Remote Sensing. J. Appl. Meteor. 2002, 40, 1118–1140. [Google Scholar] [CrossRef]
- Smith, P.L.; Kliche, D.V. The bias in moment estimators for parameters of drop-size distribution functions: Sampling from exponential distributions. J. Appl. Meteor. 2005, 44, 1195–1205. [Google Scholar] [CrossRef]
- Kliche, D.V.; Smith, P.L.; Johnson, R.W. L-Moment Estimators as Applied to Gamma Drop Size Distributions. J. Appl. Meteor. Climatol. 2008, 47, 3117–3130. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information Theory and Statistical Physics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Dumouchel, C. The Maximum Entropy Formalism and the Prediction of Liquid Spray Drop-Size Distribution. Entropy 2009, 11, 713–747. [Google Scholar] [CrossRef]
- Babinsky, E.; Sojka, P.E. Modeling drop size distributions. Progr. Energy Combust. Sci. 2002, 28, 303–329. [Google Scholar] [CrossRef]
- Tapiador, F.J. A Maximum Entropy Analysis of Global Monthly Series of Rainfall from Merged Satellite Data. Int. J. Remote Sens. 2007, 28, 1113–1121. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Kidd, C.; Levizzani, V.; Marzano, F.S. A maximum entropy approach to satellite quantitative precipitation estimation (QPE). Int. J. Remote Sens. 2004, 25, 4629–4639. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Casanova, J.L. An Algorithm for the Fusion of Images based on Jaynes Maximum Entropy Method. Int. J. Remote Sens. 2002, 23, 777–785. [Google Scholar] [CrossRef]
- Liu, Y.G.; You, L.G.; Yang, W.N.; Liu, F. On the size distribution of cloud droplets. Atmos. Res. 1995, 35, 201–216. [Google Scholar] [CrossRef]
- Liu, Y.G.; Hallett, J. On the size distribution of cloud droplets by condensation: A new conceptual model. J. Atmos. Sci. 1998, 55, 527–536. [Google Scholar] [CrossRef]
- Liu, Y.G.; Daum, P.H.; Hallett, J. A generalized Systems Theory of the effect of varying Fluctuations on cloud droplet size distributions. J. Atmos. Sci. 2002, 59, 2279–2290. [Google Scholar] [CrossRef]
- Tokay, A.; Short, D.A. Evidence from tropical raindrop spectra of the origin of rain from stratiform vs convective clouds. J. Appl. Meteor. 1996, 35, 355–371. [Google Scholar] [CrossRef]
- Brawm, D.; Upton, G. Estimation of an atmospheric gamma drop size distribution using disdrometer data. Atmos. Res. 2008, 87, 66–79. [Google Scholar] [CrossRef]
- Matsumoto, M.; Nishimura, T. Mersenne twister: A 623-dimensionally equidistributed uniform pseudo-random number generator. ACM Trans. Model. Comput. Simul. 1998, 8, 3–30. [Google Scholar] [CrossRef]
- Bringi, V.N.; Huang, G.; Chandrasekar, V.; Gorgucci, E. A methodology for estimating the parameters of a gamma raindrop size distribution model from polarimetric radar data: Application to a squall-line event from the TRMM/Brazil campaign. J. Atmos. Oceanic Technol. 2002, 19, 633–645. [Google Scholar] [CrossRef]
- Mallet, C.; Barthes, L. Estimation of Gamma Raindrop Size Distribution Parameters: Statistical Fluctuations and Estimation Errors. J. Atmos. Oceanic Technol. 2008, 26, 1572–1584. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Checa, R.; de Castro, M. An experiment to measure the spatial variability of rain drop size distribution using sixteen laser disdrometers. Geophys. Res. Lett. 2010, 37, L16803. [Google Scholar] [CrossRef]
- Smith, P.L. Raindrop size distributions. Exponential or Gamma—Does the difference matter? J. Appl. Meteor. 2003, 42, 1031–1034. [Google Scholar] [CrossRef]
- Ulbrich, C.W.; Atlas, D. Rainfall microphysics and radar properties: Analysis methods for drops size spectra. J. Appl. Meteor. 1998, 37, 912–923. [Google Scholar] [CrossRef]
- Kozu, T.; Nakamura, K. Rainfall parameter estimation from dual-radar measurements combining reflectivity profile and path-integrated attenuation. J. Atmos. Oceanic Technol. 1991, 8, 259–270. [Google Scholar] [CrossRef]
- Smith, P.L.; Kliche, D.V.; Johnson, R.W. The Bias and Error Estimators for Parameters of Drop Size Distribution Functions: Sampling from Gamma Distributions. J. Appl. Meteor. Climatol. 2009, 48, 2118–2126. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379. [Google Scholar] [CrossRef]
- Singh, V.P.; Rajagopal, A.K.; Singh, K. Derivation of some frequency distributions using the principle of maximum entropy. Adv. Water Res. 1986, 9, 91–106. [Google Scholar] [CrossRef]
- In generating the histograms, histograms of 20 bins were also computed, and, in the case of the smallest sample sizes, histograms of 10 bins were produced. Analogous general behaviour was reported in both of these cases.
- It is also possible to compare the mean value of da[0] over a large set of histograms, or to analyse the values of Da[0] for an entire precipitation event.
- This is the same number of histograms per scenario that were used in the study of [29].
- Mondal, D.; Datta, A.; Sarkar, A. Droplet size and velocity distributions in a spray from a pressure swirl atomizer: Application of maximum entropy formalism. Proc. IMechE Part C J. Mech. Eng. Sci. 2004, 218, 737–749. [Google Scholar] [CrossRef]
- Abramov, R. A practical computational framework for the multidimensional moment-constrained maximum entropy principle. J. Comp. Phys. 2006, 1, 198–209. [Google Scholar] [CrossRef]
- Abramov, R. The multidimensional moment-constrained maximum entropy problem: A BFGS algorithm with constraint scaling. J. Comp. Phys. 2009, 228, 96–108. [Google Scholar] [CrossRef]
- Tapiador, F.J. Hurricane Footprints in Global Climate Models. Entropy 2008, 10, 613–620. [Google Scholar] [CrossRef]
- Niven, R.K. Steady state of a dissipative flow-controlled system and the maximum entropy production principle. Phys. Rev. E 2009, 80, 021113–021128. [Google Scholar] [CrossRef]
- Mohammad-Djafari, A. A Matlab Program to Calculate the Maximum Entropy Distributions. Max. Entropy Bayesian Meth. 1991. arXiv:physics/0111126. [Google Scholar]
Appendix
Numerical Method for Maximise the Entropy Functional
Non-Linear Systems of Equations
Numerical Solution by Newton-Raphson Method
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Checa, R.; Tapiador, F.J. A Maximum Entropy Modelling of the Rain Drop Size Distribution. Entropy 2011, 13, 293-315. https://doi.org/10.3390/e13020293
Checa R, Tapiador FJ. A Maximum Entropy Modelling of the Rain Drop Size Distribution. Entropy. 2011; 13(2):293-315. https://doi.org/10.3390/e13020293
Chicago/Turabian StyleCheca, Ramiro, and Francisco J. Tapiador. 2011. "A Maximum Entropy Modelling of the Rain Drop Size Distribution" Entropy 13, no. 2: 293-315. https://doi.org/10.3390/e13020293





