Microcanonical Description of (Micro) Black Holes
Abstract
:1. Introduction
2. Thermodynamical Interpretation of Black Holes
3. Black Holes in D Dimensions
4. Quantum Field Theory on Black Hole Backgrounds
4.1. Canonical Formulation
4.2. Microcanonical Formulation
5. Hawking Effect
5.1. Thermal Vacuum
5.2. Microcanonical Vacuum
6. Micro-Black Hole Decay Rates
6.1. ADD Scenario
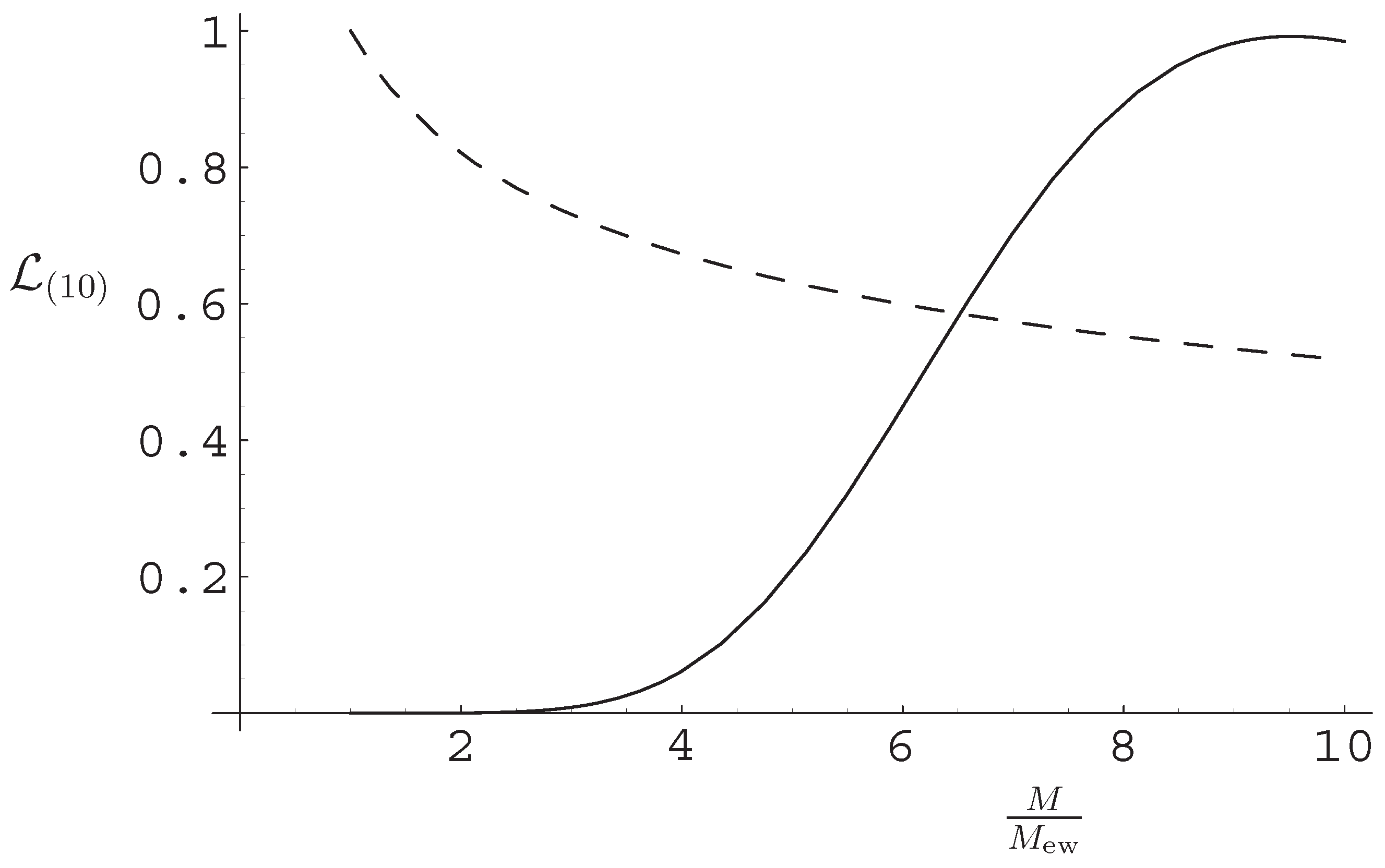
6.2. RS Scenario
7. Summary
References
- Harms, B.; Leblanc, Y. Statistical mechanics of black holes. Phys. Rev. D 1992, 46, 2334–2340. [Google Scholar] [CrossRef]
- Harms, B.; Leblanc, Y. Statistical mechanics of extended black objects. Phys. Rev. D 1993, 47, 2438–2445. [Google Scholar] [CrossRef]
- Harms, B.; Leblanc, Y. Complete semiclassical treatment of the quantum black hole problem. Ann. Phys. 1995, 244, 262–271. [Google Scholar] [CrossRef]
- Harms, B.; Leblanc, Y. Proper field quantization in black hole space-times. Ann. Phys. 1995, 244, 272–282. [Google Scholar] [CrossRef]
- Cox, P.H.; Harms, B.; Leblanc, Y. Dilatonic black holes, naked singularities and strings. Europhys. Letts. 1994, 26, 321–326. [Google Scholar] [CrossRef]
- Harms, B.; Leblanc, Y. Black extended objects, naked singularities and P-branes. Europhys. Letts. 1994, 27, 557–562. [Google Scholar] [CrossRef]
- Harms, B.; Leblanc, Y. Conjectures on nonlocal effects in string black holes. Ann. Phys. 1995, 242, 265–274. [Google Scholar] [CrossRef]
- Casadio, R.; Harms, B.; Leblanc, Y. Statistical mechanics of Kerr-Newman dilaton black holes and the bootstrap condition. Phys. Rev. D 1998, 57, 1309–1312. [Google Scholar] [CrossRef]
- Casadio, R.; Harms, B.; Leblanc, Y. Microfield dynamics of black holes. Phys. Rev. D 1998, 58, 044014. [Google Scholar] [CrossRef]
- Cavaglia, M. Black hole and brane production in TeV gravity: A Review. Int. J. Mod. Phys. A 2003, 18, 1843–1882. [Google Scholar] [CrossRef]
- Kanti, P. Black holes in theories with large extra dimensions: A Review. Int. J. Mod. Phys. A 2004, 19, 4899–4951. [Google Scholar] [CrossRef]
- Whisker, R. Braneworld black holes. arXiv, 2008; arXiv:0810.1534, [gr-qc]. [Google Scholar]
- Gregory, R. Braneworld black holes. Lect. Notes Phys. 2009, 769, 259–298. [Google Scholar]
- Emparan, R.; Horowitz, G.T.; Myers, R.C. Exact description of black holes on branes. JHEP 2000, 0001, 007. [Google Scholar] [CrossRef]
- Shiromizu, T.; Shibata, M. Black holes in the brane world: Time symmetric initial data. Phys. Rev. D 2000, 62, 127502. [Google Scholar] [CrossRef]
- Chamblin, A.; Reall, H.S.; Shinkai, H.-a.; Shiromizu, T. Charged brane world black holes. Phys. Rev. D 2001, 63, 064015. [Google Scholar] [CrossRef]
- Casadio, R.; Fabbri, A.; Mazzacurati, L. New black holes in the brane world? Phys. Rev. D 2002, 65, 084040. [Google Scholar] [CrossRef]
- Kanti, P.; Tamvakis, K. Quest for localized 4-D black holes in brane worlds. Phys. Rev. D 2002, 65, 084010. [Google Scholar] [CrossRef]
- Kudoh, H.; Tanaka, T.; Nakamura, T. Small localized black holes in brane world: Formulation and numerical method. Phys. Rev. D 2003, 68, 024035. [Google Scholar] [CrossRef]
- Casadio, R.; Mazzacurati, L. Bulk shape of brane world black holes. Mod. Phys. Lett. A 2003, 18, 651–660. [Google Scholar] [CrossRef]
- Creek, S.; Gregory, R.; Kanti, P.; Mistry, B. Braneworld stars and black holes. Class. Quant. Grav. 2006, 23, 6633–6658. [Google Scholar] [CrossRef]
- Dai, D.C.; Stojkovic, D. Analytic solution for a static black hole in RSII model. arXiv, 2010; arXiv:1004.3291, [gr-qc]. [Google Scholar]
- Dadhich, N.; Maartens, R.; Papadopoulos, P.; Rezania, V. Black holes on the brane. Phys. Lett. B 2000, 487, 1–6. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G.R. The Hierarchy problem and new dimensions at a millimeter. Phys. Lett. B 1998, 429, 263–272. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G.R. Phenomenology, astrophysics and cosmology of theories with submillimeter dimensions and TeV scale quantum gravity. Phys. Rev. D 1999, 59, 086004. [Google Scholar] [CrossRef]
- Antoniadis, I.; Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G.R. New dimensions at a millimeter to a Fermi and superstrings at a TeV. Phys. Lett. B 1998, 436, 257–263. [Google Scholar] [CrossRef]
- Randall, L.; Sundrum, R. An Alternative to compactification. Phys. Rev. Lett. 1999, 83, 4690–4693. [Google Scholar] [CrossRef]
- Argyres, P.C.; Dimopoulos, S.; March-Russell, J. Black holes and submillimeter dimensions. Phys. Lett. B 1998, 441, 96–104. [Google Scholar] [CrossRef]
- Dimopoulos, S.; Landsberg, G.L. Black holes at the LHC. Phys. Rev. Lett. 2001, 87, 161602. [Google Scholar] [CrossRef] [PubMed]
- Giddings, S.B.; Thomas, S.D. High-energy colliders as black hole factories: The end of short distance physics. Phys. Rev. D 2002, 65, 056010. [Google Scholar] [CrossRef]
- Harris, C.M.; Richardson, P.; Webber, B.R. CHARYBDIS: A Black hole event generator. JHEP 2003, 0308, 033. [Google Scholar] [CrossRef]
- Alberghi, G.L.; Casadio, R.; Tronconi, A. Quantum gravity effects in black holes at the LHC. J. Phys. G 2007, 34, 767–778. [Google Scholar] [CrossRef]
- Cavaglia, M.; Godang, R.; Cremaldi, L.; Summers, D. Catfish: A Monte Carlo simulator for black holes at the LHC. Comput. Phys. Commun. 2007, 177, 506–517. [Google Scholar] [CrossRef]
- Dai, D.C.; Starkman, G.; Stojkovic, D.; Issever, C.; Rivzi, E.; Tseng, J. BlackMax: A black-hole event generator with rotation, recoil, split branes, and brane tension. Phys. Rev. D 2008, 77, 076007. [Google Scholar] [CrossRef]
- Frost, J.A.; Gaunt, J.R.; Sampaio, M.O.P.; Casals, M.; Dolan, S.R.; Parker, M.A.; Webber, B.R. Phenomenology of production and decay of spinning extra-dimensional black holes at hadron colliders. JHEP 2009, 0910, 014. [Google Scholar] [CrossRef]
- Gingrich, D.M. Quantum black holes with charge, colour, and spin at the LHC. J. Phys. G 2010, 37, 105108. [Google Scholar] [CrossRef]
- Gingrich, D.M. Production of tidal-charged black holes at the Large Hadron Collider. Phys. Rev. D 2010, 81, 057702. [Google Scholar] [CrossRef]
- Casadio, R.; Nicolini, P. The decay-time of non-commutative micro-black holes. JHEP 2008, 0811, 072. [Google Scholar] [CrossRef]
- Casadio, R.; Harms, B. Black Hole Evaporation and Compact Extra Dimensions. Phys. Rev. D 2001, 64, 024016. [Google Scholar] [CrossRef]
- Casadio, R.; Harms, B. Black hole evaporation and large extra dimensions. Phys. Lett. B 2000, 487, 209–214. [Google Scholar] [CrossRef]
- Casadio, R.; Harms, B. Can black holes and naked singularities be detected in accelerators? Int. J. Mod. Phys. A 2002, 17, 4635–4646. [Google Scholar] [CrossRef]
- Casadio, R.; Fabi, S.; Harms, B. Possibility of catastrophic black hole growth in the warped brane-world scenario at the LHC. Phys. Rev. D 2009, 80, 084036. [Google Scholar] [CrossRef]
- Casadio, R.; Fabi, S.; Harms, B.; Micu, O. Theoretical survey of tidal-charged black holes at the LHC. JHEP 2010, 1002, 079. [Google Scholar] [CrossRef]
- Casadio, R.; Micu, O. Exploring the bulk of tidal charged micro-black holes. Phys. Rev. D 2010, 81, 104024. [Google Scholar] [CrossRef]
- Casadio, R.; Harms, B.; Micu, O. Effect of brane thickness on microscopic tidal-charged black holes. Phys. Rev. D 2010, 82, 044026. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black holes and entropy. Phys. Rev. D 1973, 7, 2333–2346. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Generalized second law of thermodynamics in black hole physics. Phys. Rev. D 1974, 9, 3292–3300. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Carter, B.; Hawking, S.W. The four laws of black hole mechanics. Commun. Math. Phys. 1973, 31, 161–170. [Google Scholar] [CrossRef]
- Chavanis, P.H. Phase transitions in self-gravitating systems. Int. J. Mod. Phys. B 2006, 20, 3113–3198. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black holes. Comm. Math. Phys. 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Hawking, S.W. Action integrals and partition functions in quantum gravity. Phys. Rev. D 1977, 15, 2752–2756. [Google Scholar] [CrossRef]
- Hossenfelder, S.; Bleicher, M.; Hofmann, S.; Stoeker, H.; Kotval, A.V. Black hole relics in large extra dimensions. Phys. Lett. B 2003, 566, 233–239. [Google Scholar] [CrossRef]
- Koch, B.; Bleicher, M.; Hossenfelder, S. Black hole remnants at the LHC. JHEP 2005, 0510, 053. [Google Scholar] [CrossRef]
- Scardigli, F.; Gruber, C.; Chen, P. Black hole remnants in the early universe. arXiv, 2010; arXiv:1009.0882, [gr-qc]. [Google Scholar]
- Nicolini, P. Noncommutative black holes, the final appeal to quantum gravity: A review. Int. J. Mod. Phys. A 2009, 24, 1229–1308. [Google Scholar] [CrossRef]
- Parikh, M.K.; Wilczek, F. Hawking radiation as tunneling. Phys. Rev. Lett. 2000, 85, 5042–5045. [Google Scholar] [CrossRef] [PubMed]
- Parikh, M.K. A Secret tunnel through the horizon. Int. J. Mod. Phys. D 2004, 13, 2351–2354. [Google Scholar] [CrossRef]
- Myers, R.C.; Perry, M.J. Black holes in higher dimensional space-times. Annals Phys. 1986, 172, 304. [Google Scholar] [CrossRef]
- Fubini, S.; Hanson, A.J.; Jackiw, R. New approach to field theory. Phys. Rev. D 1973, 7, 1732–1760. [Google Scholar] [CrossRef]
- Dethlefsen, J.; Nielsen, H.B.; Tze, H.C. The hagedorn spectrum distribution and the dimension of hadronic matter. Phys. Lett. B 1974, 48, 48–50. [Google Scholar] [CrossRef]
- Strumia, A.; Venturi, G. Are hadrons strings? Lett. Nuovo Cimento 1975, 13, 337. [Google Scholar] [CrossRef]
- Umezawa, H.; Matsumoto, H.; Tachiki, M. Thermo Field Dynamics and Condensed States; North-Holland Publishing Co.: Amsterdam, The Netherland, 1982. [Google Scholar]
- Hagedorn, R. Statistical thermodynamics of strong interactions at high-energies. Nuovo Cimento Suppl. 1965, 3, 147–186. [Google Scholar]
- Frautschi, S.C. Statistical bootstrap model of hadrons. Phys. Rev. D 1971, 3, 2821–2834. [Google Scholar] [CrossRef]
- Carlitz, R.D. Hadronic matter at high density. Phys. Rev. D 1972, 5, 3231–3242. [Google Scholar] [CrossRef]
- Kubo, R. Statistical Mechanics; Norht-Holland Publishing Co.: Amsterdam, The Netherland, 1980. [Google Scholar]
- Leblanc, Y. Statistical field dynamics. Unpublished material. Available online: http://www.efieldtheory.com/articles/?eFTC=020701 (accessed on 1 September 2010).
- Birrell, N.D.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Carr, B.J.; MacGibbon, J.H. Cosmic rays from primordial black holes and constraints on the early universe. Phys. Rept. 1998, 307, 141–154. [Google Scholar] [CrossRef]
- Kotwal, A.V.; Hofmann, S. Discrete energy spectrum of Hawking radiation from Schwarzschild surfaces. arXiv, 2002; [hep-ph/0204117]. [Google Scholar]
- Gingrich, D.M.; Martell, K. Microcanonical treatment of black hole decay at the Large Hadron Collider. J. Phys. G Nucl. Part. Phys. 2008, 35, 035001. [Google Scholar] [CrossRef]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/.)
Share and Cite
Casadio, R.; Harms, B. Microcanonical Description of (Micro) Black Holes. Entropy 2011, 13, 502-517. https://doi.org/10.3390/e13020502
Casadio R, Harms B. Microcanonical Description of (Micro) Black Holes. Entropy. 2011; 13(2):502-517. https://doi.org/10.3390/e13020502
Chicago/Turabian StyleCasadio, Roberto, and Benjamin Harms. 2011. "Microcanonical Description of (Micro) Black Holes" Entropy 13, no. 2: 502-517. https://doi.org/10.3390/e13020502




