Geometry of q-Exponential Family of Probability Distributions
Abstract
:1. Introduction
2. q-Gibbs or q-Exponential Family of Distributions
2.1. q-Logarithm and q-Exponential Function
2.2. q-Exponential Family
2.3. q-Potential Function
2.4. q-Divergence
2.5. q-Riemannian Metric
3. Dually Flat Structure of q-Exponential Family
3.1. Legendre Transformation and q-Entropy
3.2. q-Dually Flat Structure
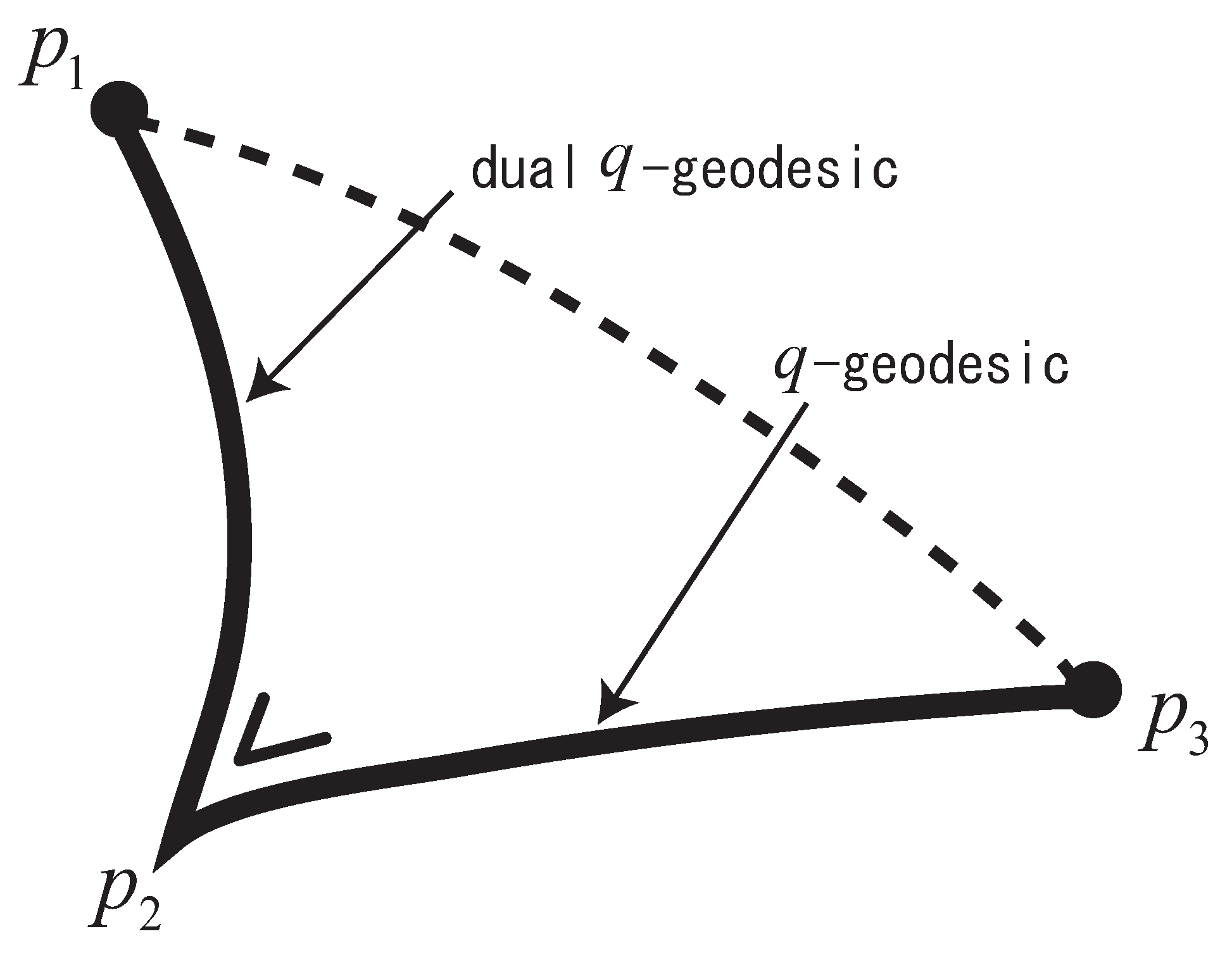
4. q-Pythagorean and q-Max-Ent Theorems
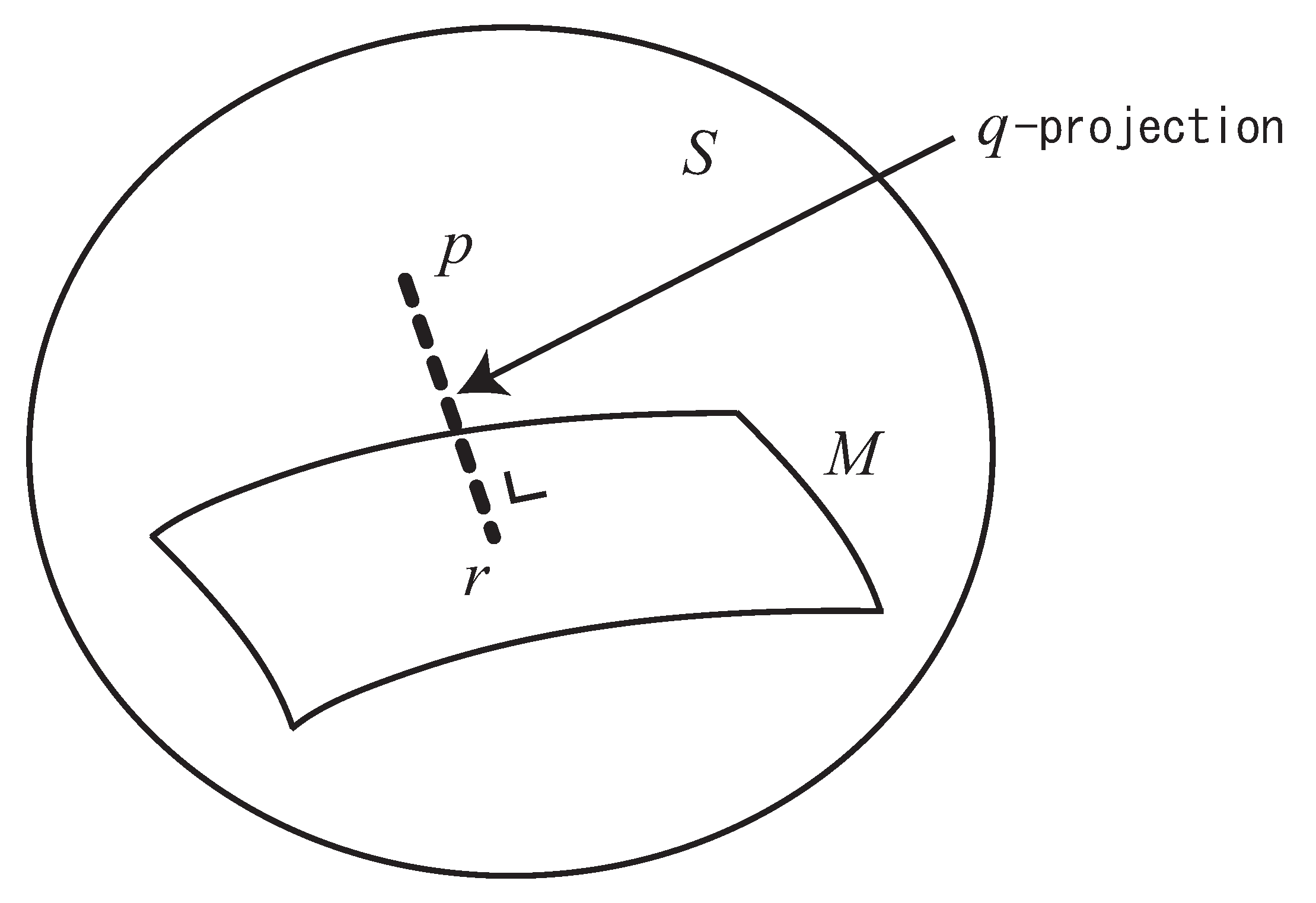
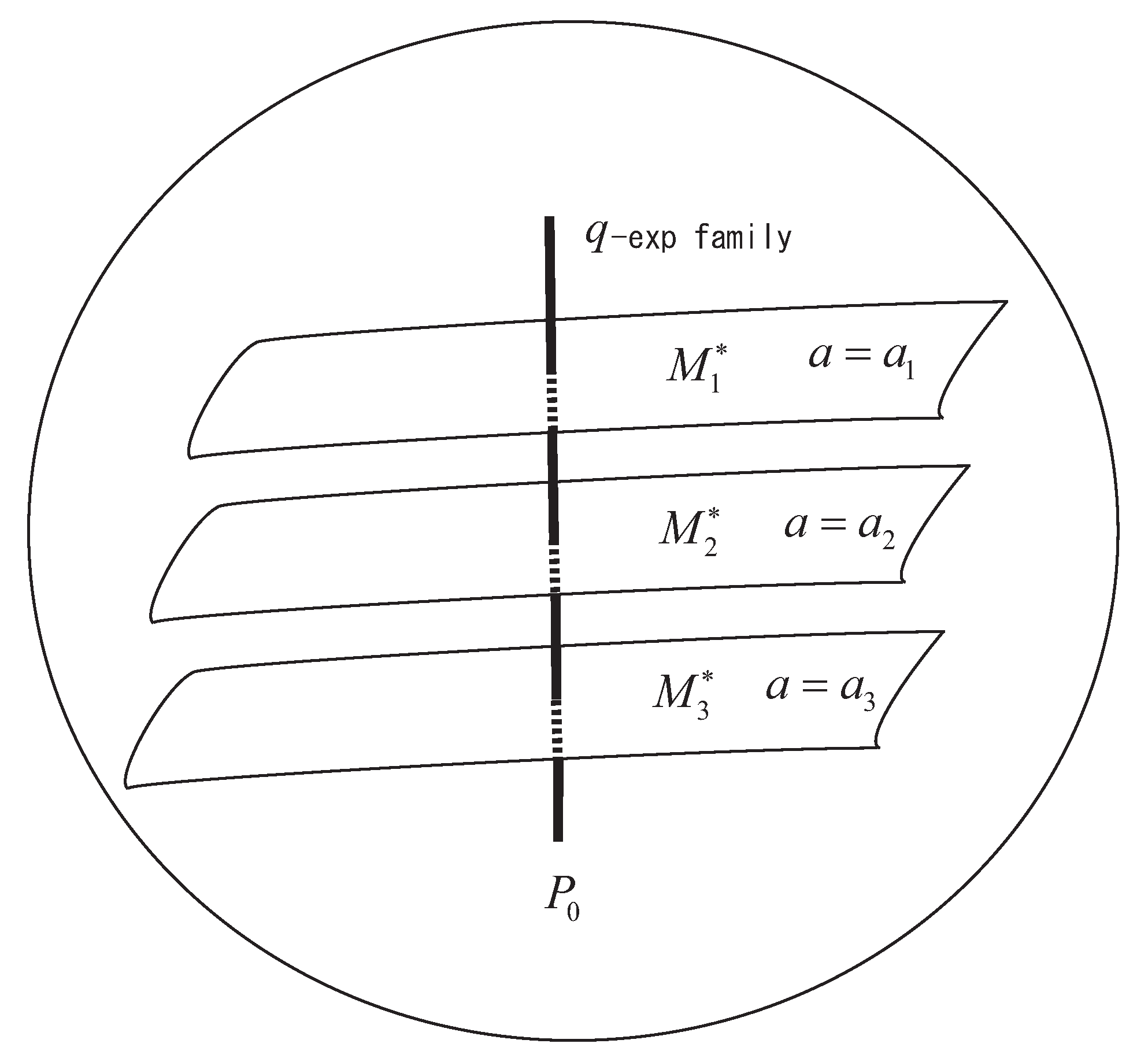
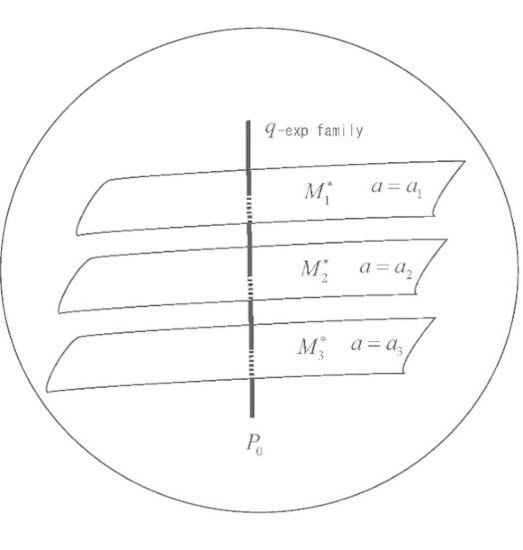
5. q-Bayesian MAP Estimator
6. Conclusions
References
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics; Springer: New York, NY, USA, 2009. [Google Scholar]
- Naudts, J. Generalised Thermostatistics; Springer: London, UK, 2011. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Naudts, J. The q-exponential family in statistical Physics. Cent. Eur. J. Phys. 2009, 7, 405–413. [Google Scholar] [CrossRef]
- Suyari, H. Mathematical structures derived from the q-multinomial coefficient in Tsallis statistics. Physica A 2006, 368, 63–82. [Google Scholar] [CrossRef]
- Suyari, H.; Wada, T. Multiplicative duality, q-triplet and μ, ν, q-relation derived from the one-to-one correspondence between the (μ, ν)-multinomial coefficient and Tsallis entropy Sq. Physica A 2008, 387, 71–83. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E. Information and Exponential Families in Statistical Theory; Wiley: New York, NY, USA, 1978. [Google Scholar]
- Amari, S.; Nagaoka, H. Methods of Information Geometry (Translations of Mathematical Monographs); Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Ohara, A. Geometry of distributions associated with Tsallis statistics and properties of relative entropy minimization. Phys. Lett. A 2007, 370, 184–193. [Google Scholar] [CrossRef]
- Furuichi, S. On the maximum entropy principle and the minimization of the Fisher information in Tsallis statistics. J. Math. Phys. 2009, 50, 013303. [Google Scholar] [CrossRef]
- Ohara, A. Geometric study for the Legendre duality of generalized entropies and its application to the porous medium equation. Eur. Phys. J. B 2009, 70, 15–28. [Google Scholar] [CrossRef]
- Ohara, A.; Matsuzoe, H.; Amari, S. A dually flat structure with escort probability and its application to alpha-Voronoi diagrams. In arXiv; 2010; arXiv:cond-mat/1010.4965. [Google Scholar]
- Kurose, T. On the Divergence of 1-conformally Flat Statistical Manifolds. Tôhoku Math. J. 1994, 46, 427–433. [Google Scholar] [CrossRef]
- Matsuzoe, H. Geometry of contrast functions and conformal geometry. Hiroshima Math. J. 1999, 29, 175–191. [Google Scholar]
- Kurose, T. Conformal-projective geometry of statistical manifolds. Interdisciplinary Information Sciences 2002, 8, 89–100. [Google Scholar] [CrossRef]
- Yamano, T. Information theory based on non-additive information content. Phys. Rev. E 2001, 63, 046105. [Google Scholar] [CrossRef]
- Naudts, J. Estimators, escort probabilities, and phi-exponential families in statistical physics. J. Ineq. Pure Appl. Math. 2004, 5, 102. [Google Scholar]
- Pistone, G. kappa-exponential models from the geometrical viewpoint. Eur. Phys. J. B 2009, 70, 29–37. [Google Scholar] [CrossRef]
- Naudts, J. Generalized exponential families and associated entropy functions. Entropy 2008, 10, 131–149. [Google Scholar] [CrossRef]
- Kaniadakis, G.; Lissia, M.; Scarfone, A.M. Deformed logarithms and entropies. Physica A 2004, 340, 41–49. [Google Scholar] [CrossRef]
- Yamano, T. Some properties of q-logarithmic and q-exponential functions in Tsallis statistics. Physica A 2002, 305, 486–496. [Google Scholar] [CrossRef]
- Tsallis, C.; Levy, S.V.F.; Souza, A.M.C.; Maynard, R. Statistical-mechanical foundation of the ubiquity of Levy distributions in nature. Phys. Rev. Lett. 1995, 75, 3589–3593, Erratum Phys. Rev. Lett. 1996, 77, 5442.. [Google Scholar] [CrossRef]
- Tanaka, M. A consideration on the family of q-Gaussian distributions. IEICE (Japan) 2002, J85–D2, 161–173. (in Japanese). [Google Scholar]
- Zhang, Z.; Zhong, F.; Sun, H. Information geometry of the power inverse Gaussian distribution. Appl. Sci. 2007, 9, 194–203. [Google Scholar]
- Ohara, A.; Wada, T. Information geometry of q-Gaussian densities and behaviors of solutions to related diffusion equations. J. Phys. A: Math. Theor. 2010, 43, 035002. [Google Scholar] [CrossRef]
- Wada, T. Generalized log-likelihood functions and Bregman divergences. J. Math. Phys. 2009, 50, 113301. [Google Scholar] [CrossRef]
- Cichocki, A.; Cruces, S.; Amari, S. Generalized alpha-beta divergences and their application to robust nonnegative matrix factorization. Entropy 2011, 13, 134–170. [Google Scholar] [CrossRef]
- Amari, S. α-divergence is unique, belonging to both f-divergence and Bregman divergence classes. IEEE Trans. Inform. Theor. 2009, 55, 4925–4931. [Google Scholar] [CrossRef]
- Beck, C.; Schlögl, F. Thermodynamics of Chaotic Systems; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Borland, L.; Plastino, A.R.; Tsallis, C. Information gain within nonextensive thermostatistics. J. Math. Phys. 1998, 39, 6490–6501. [Google Scholar] [CrossRef]
- Furuichi, S. Fundamental properties of Tsallis relative entropy. J. Math. Phys. 2004, 45, 4868–4877. [Google Scholar] [CrossRef]
- Okamoto, I.; Amari, S.; Takeuchi, K. Asymptotic theory of sequential estimation procedures for curved exponential families. Ann. Stat. 1991, 19, 961–981. [Google Scholar] [CrossRef]
- Rényi, A. On measures of entropy and information. In Proceedings of the 4th Berkeley Symposium on Mathematics, Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960; pp. 547–561.
- Landsberg, P.T.; Vedral, V. Distributions and channel capacities in generalized statistical mechanics. Phys. Lett. A 1998, 247, 211–217. [Google Scholar] [CrossRef]
- Rajagopal, A.K.; Abe, S. Implications of form invariance to the structure of nonextensive entropies. Phys. Rev. Lett. 1999, 83, 1711–1714. [Google Scholar] [CrossRef]
- Yamano, T. Source coding theorem based on a nonadditive information content. Physica A 2002, 305, 190–195. [Google Scholar] [CrossRef]
- Wada, T.; Scarfone, A.M. Connections between Tsallis’ formalisms employing the standard linear average energy and ones employing the normalized q-average energy. Phys. Lett. A 2005, 335, 351–362. [Google Scholar] [CrossRef]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Amari, S.-i.; Ohara, A. Geometry of q-Exponential Family of Probability Distributions. Entropy 2011, 13, 1170-1185. https://doi.org/10.3390/e13061170
Amari S-i, Ohara A. Geometry of q-Exponential Family of Probability Distributions. Entropy. 2011; 13(6):1170-1185. https://doi.org/10.3390/e13061170
Chicago/Turabian StyleAmari, Shun-ichi, and Atsumi Ohara. 2011. "Geometry of q-Exponential Family of Probability Distributions" Entropy 13, no. 6: 1170-1185. https://doi.org/10.3390/e13061170