Joint Markov Blankets in Feature Sets Extracted from Wavelet Packet Decompositions
Abstract
:1. Introduction
2. Feature Extraction from Wavelet Packet Decomposition
2.1. Wavelet Coefficient Features
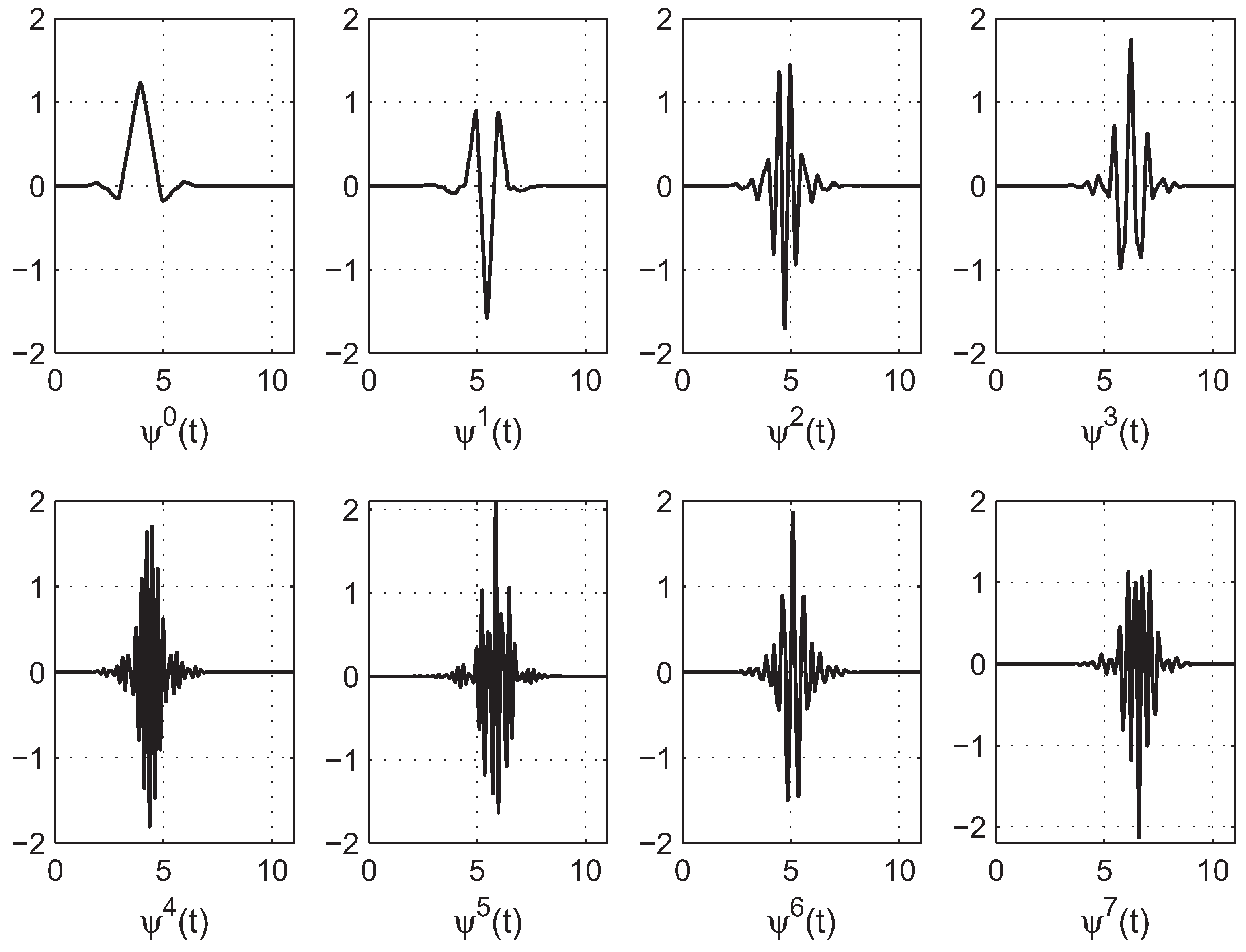
2.2. Wavelet Energy Features
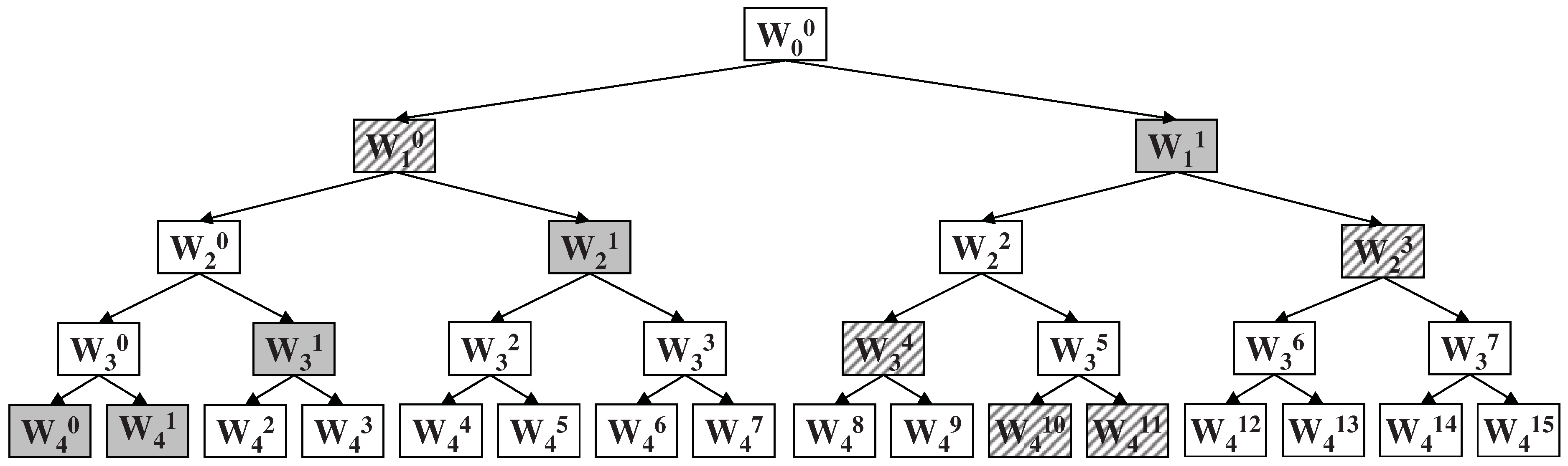
2.3. Dependencies between Wavelet Features
3. Markov Blanket Filtering: A Link with Information-Theoretic Approaches
4. Joint Markov Blankets in Wavelet Feature Sets
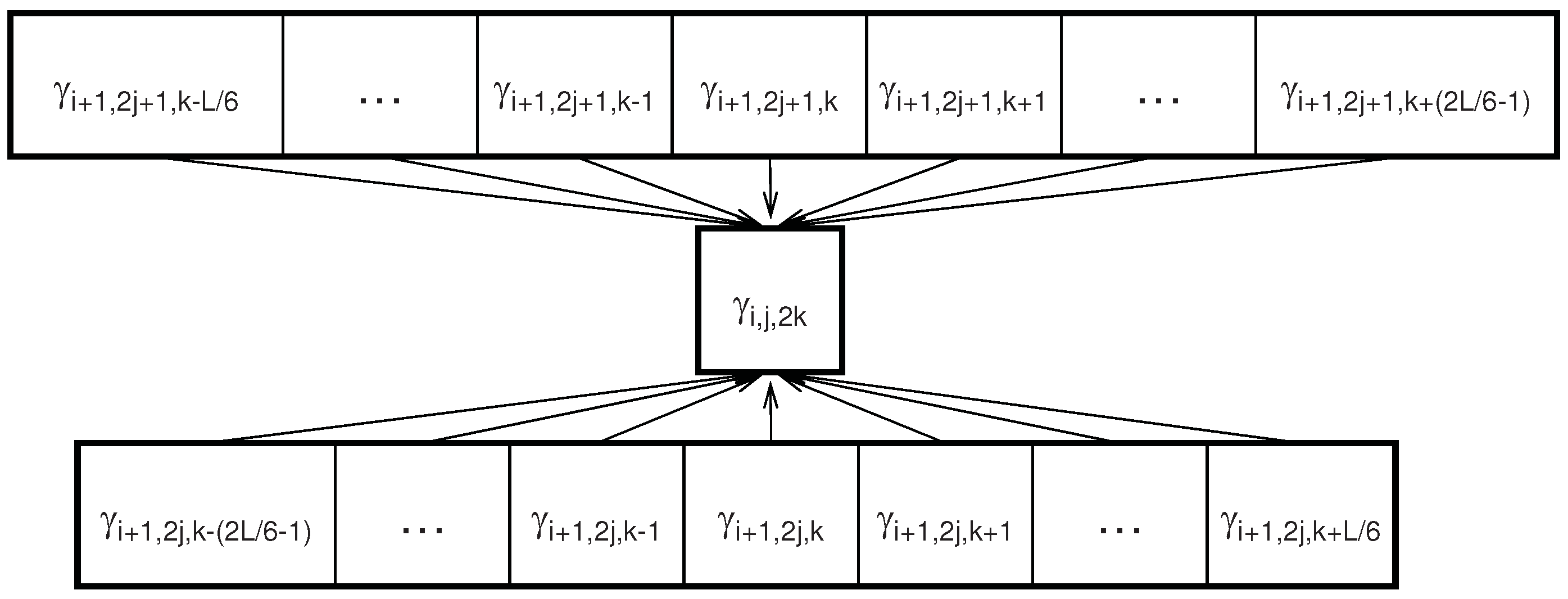
4.1. Parents or Children Nodes are Joint Markov Blankets
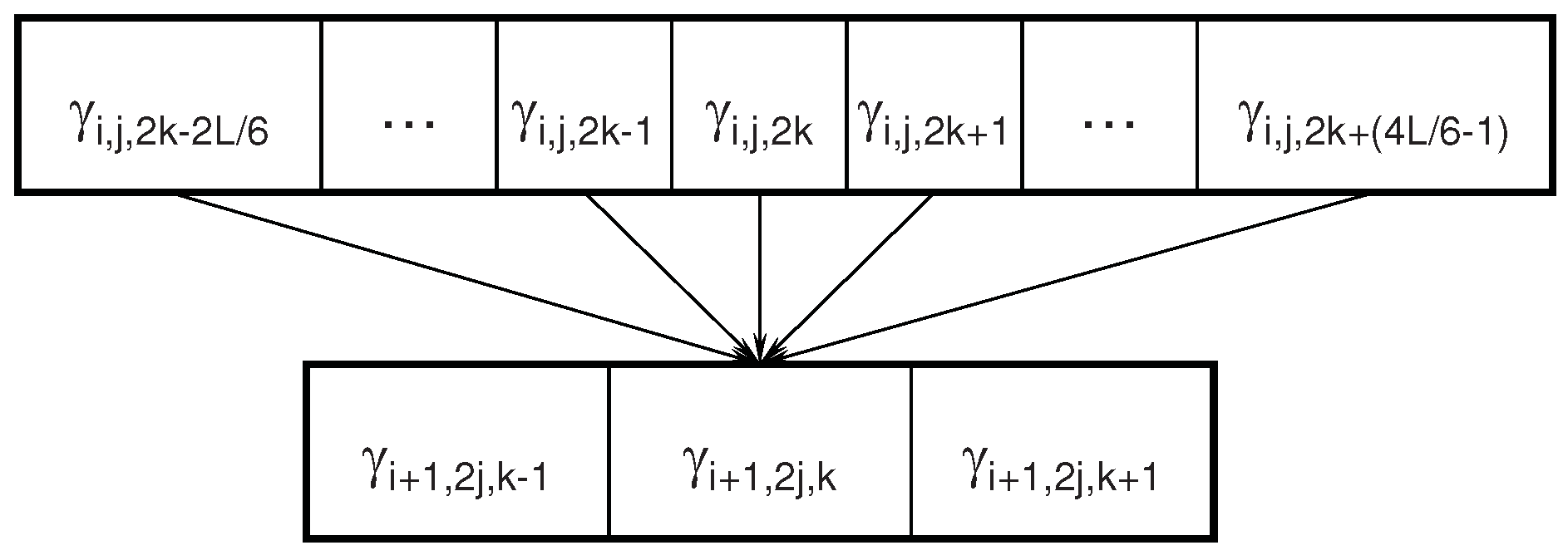
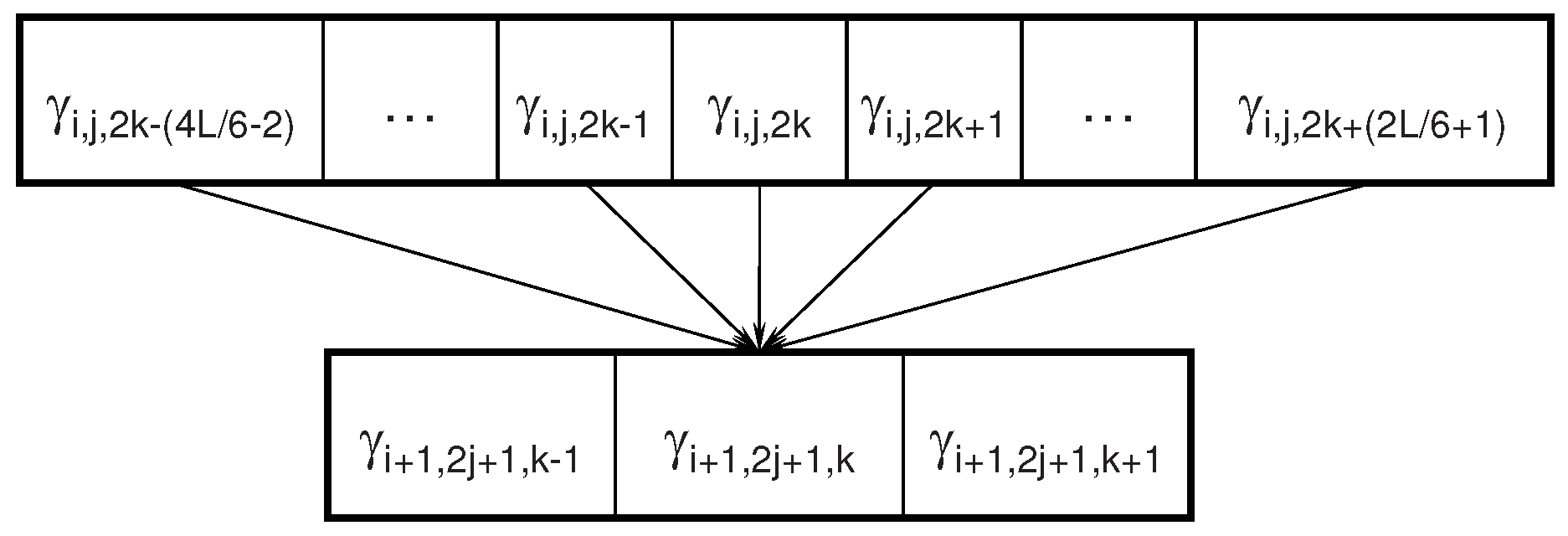
4.2. Child Nodes are Joint Markov Blankets for Energy Features
4.3. Experiments with Energy Features of Wavelet Packet Decomposition
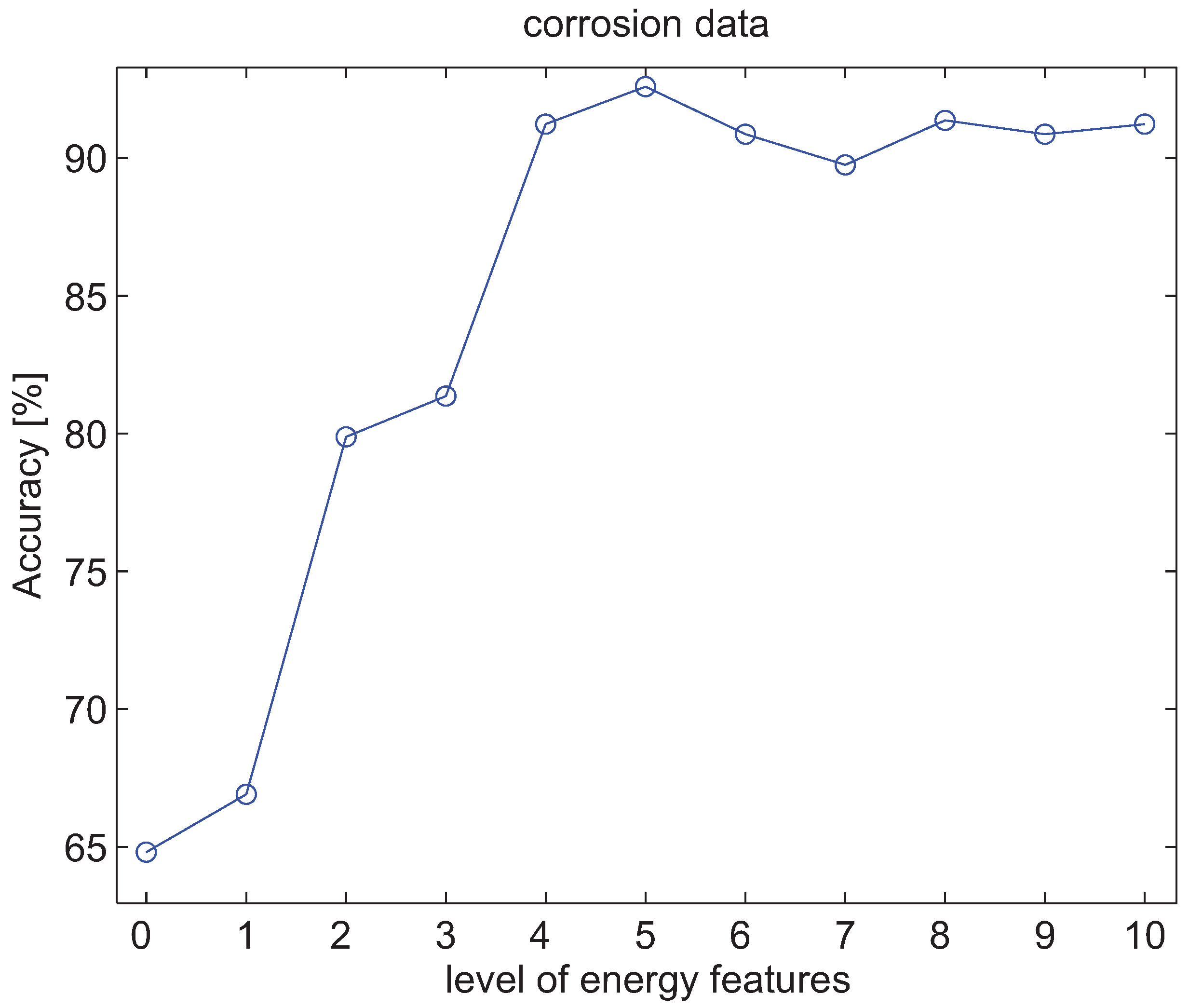

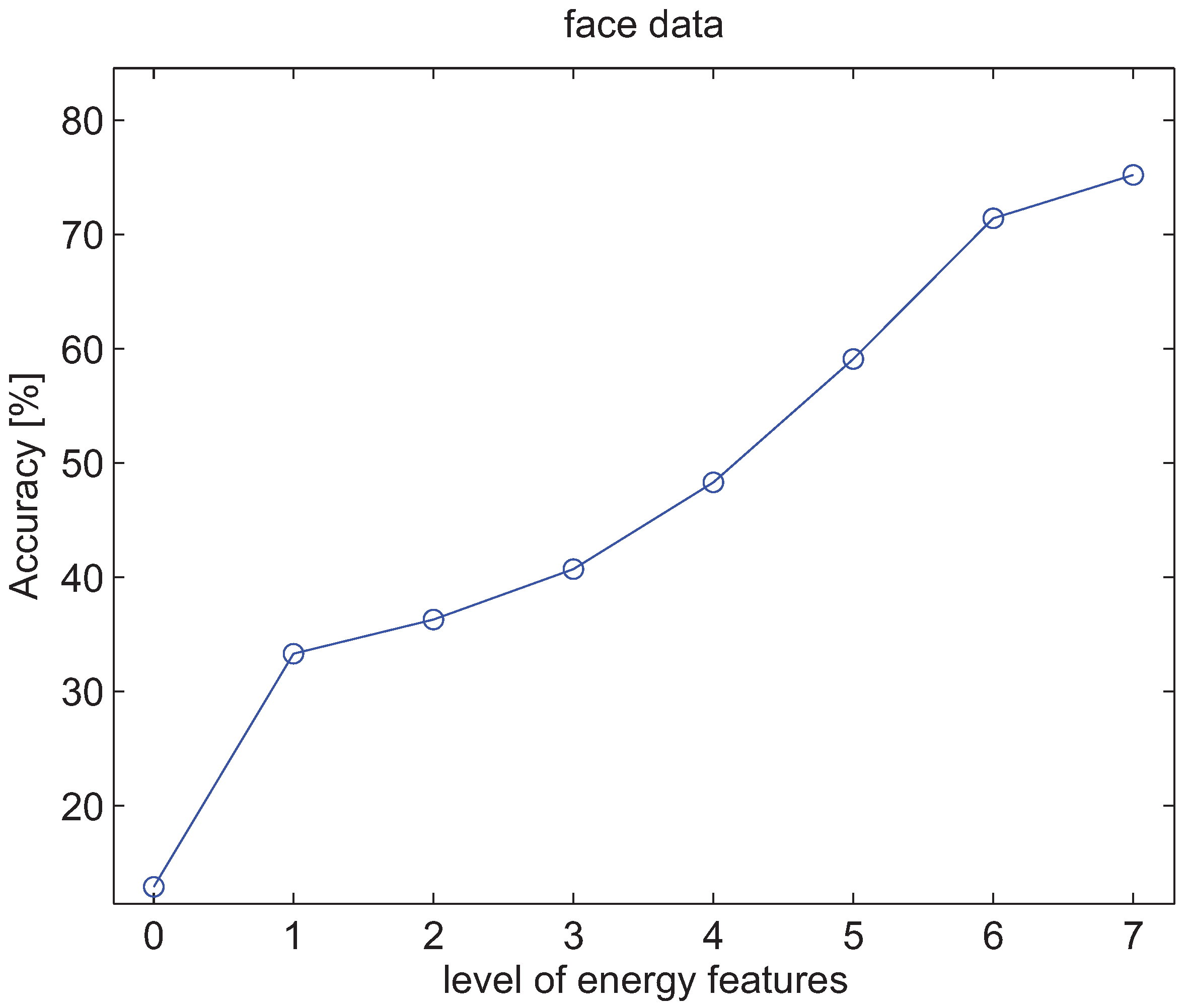
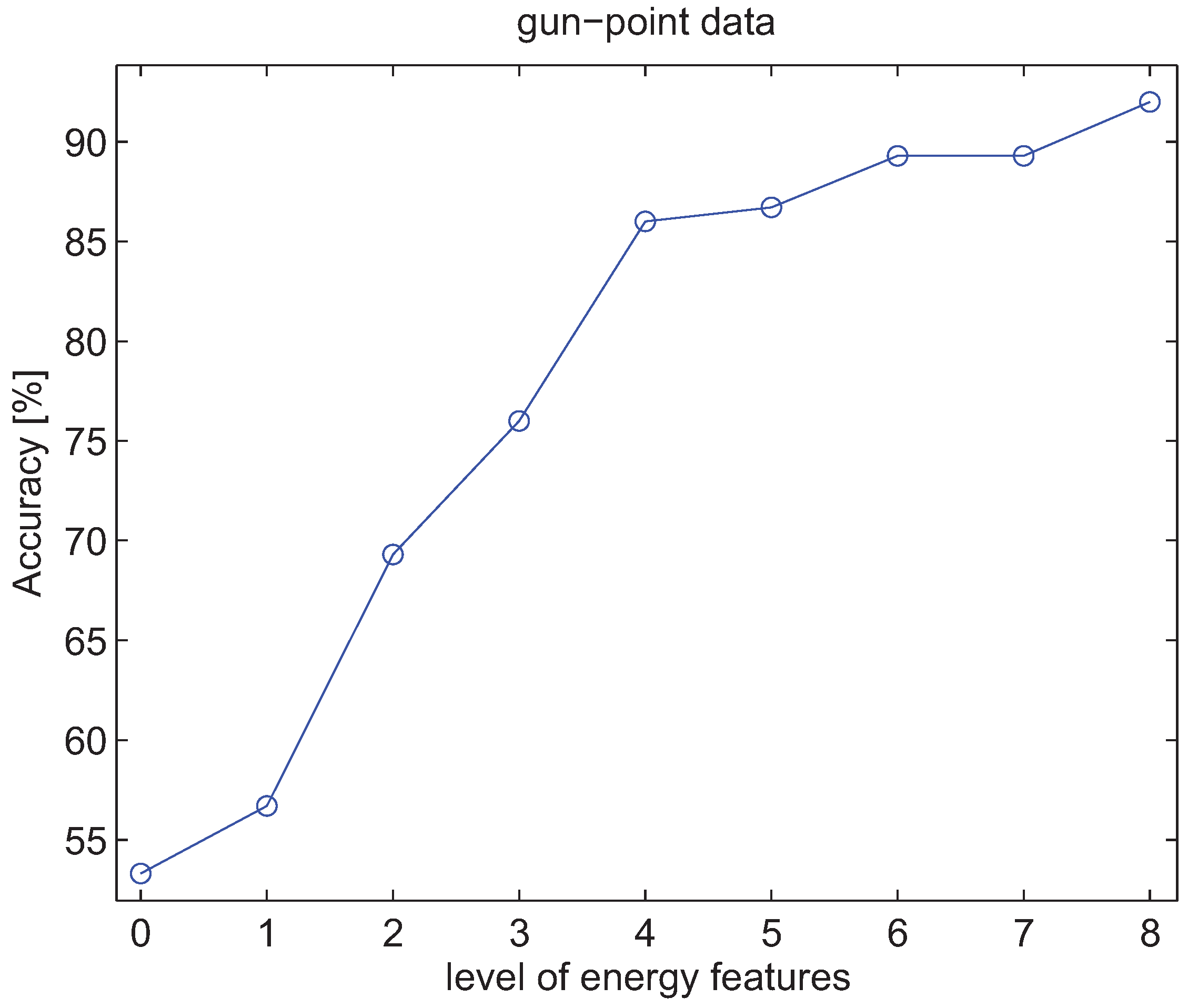
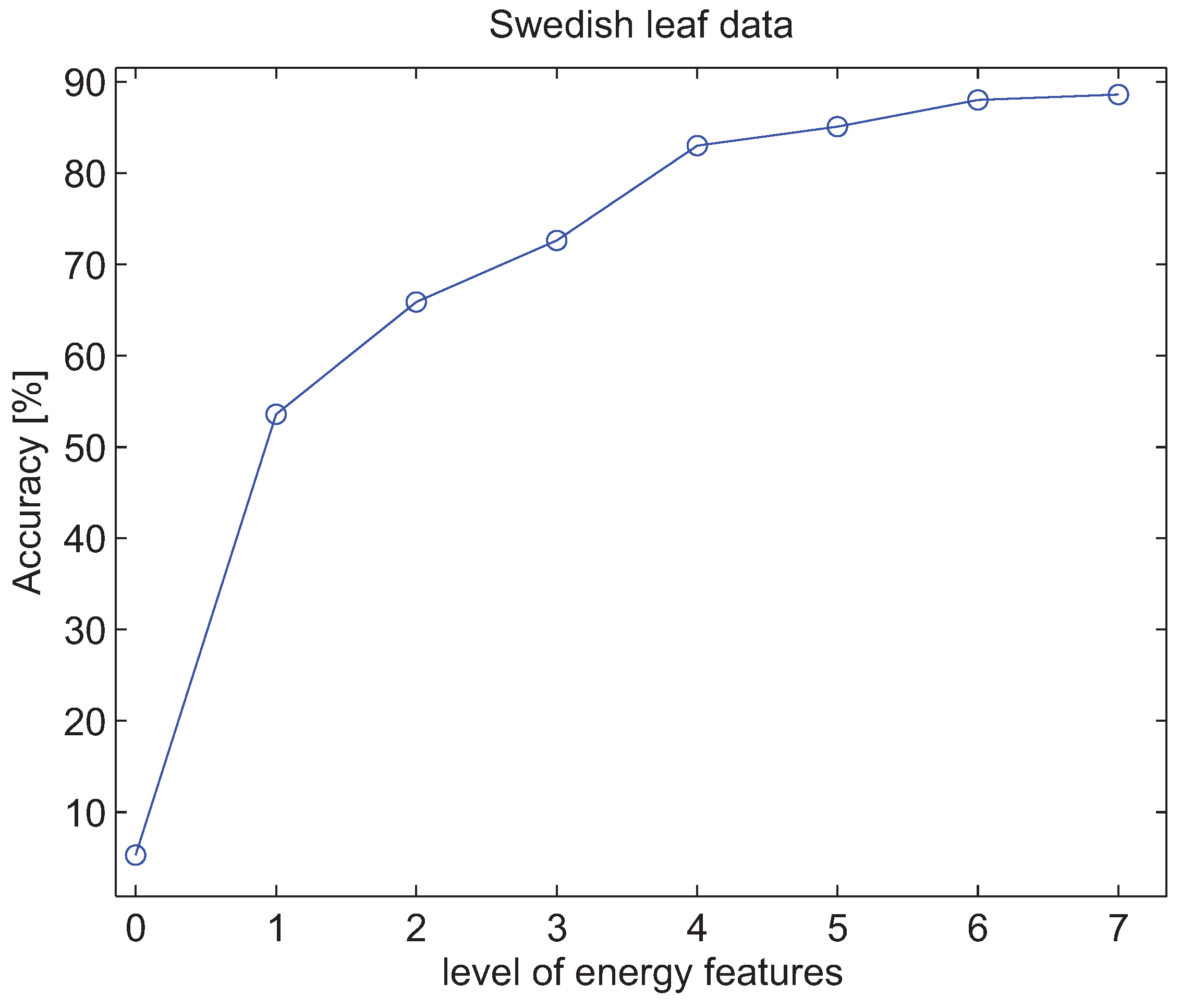
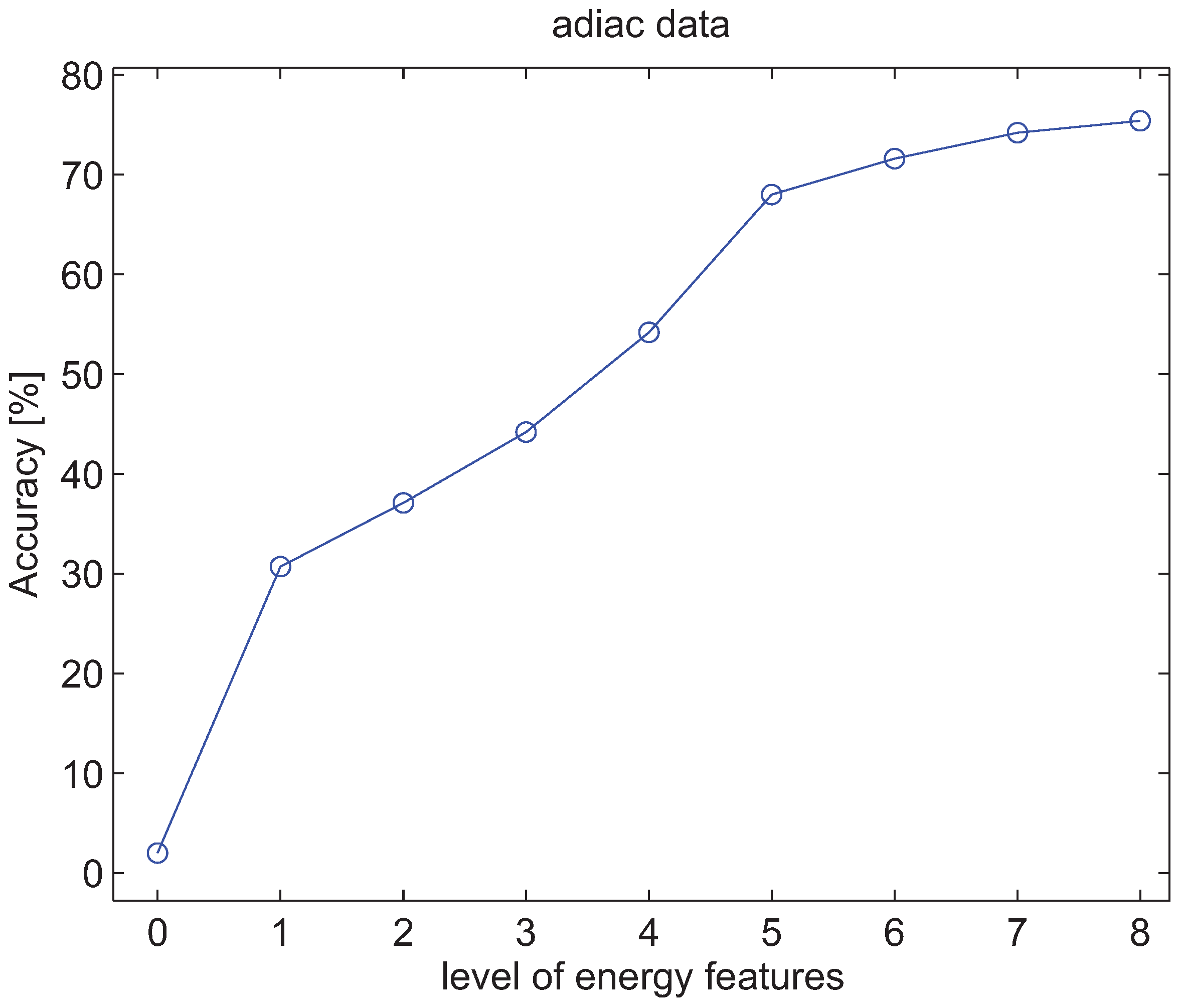
5. Conclusions
Acknowledgments
References
- Coifman, R.R.; Meyer, Y. Orthonormal wave packet bases; Technical report; Yale University, 1990. [Google Scholar]
- Mallat, S. A theory for multiresolution signal decomposition: The wavelet decomposition. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing; Academic Press: New York, NY, USA, 1998. [Google Scholar]
- Wickerhauser, M.V. INRIA lectures on wavelet packet algorithms. In Proceedings of Ondelettes et Paquets d’Ondes; 17–21 June 1991; Lions, P.L., Ed.; INRIA: Rocquencourt, France; pp. 31–99.
- Coifman, R.R.; Wickerhauser, M.V. Entropy-based algorithm for best basis selection. IEEE Trans. Inf. Theory 1992, 38, 713–718. [Google Scholar] [CrossRef]
- Saito, N.; Coifman, R.R. Local discriminant bases and their applications. J. Math. Imaging Vis. 1995, 5, 337–358. [Google Scholar] [CrossRef]
- Saito, N.; Coifman, R.R. Geological information extraction from acoustic well-logging waveforms using time-frequency wavelets. Geophysics 1997, 62, 1921–1930. [Google Scholar] [CrossRef]
- Saito, N.; Coifman, R.R.; Geshwind, F.B.; Warner, F. Discriminant feature extraction using empirical probability density estimation and a local basis library. Pattern Recogn. 2002, 35, 2481–2852. [Google Scholar] [CrossRef]
- Van Dijck, G.; Van Hulle, M.M. Wavelet packet decomposition for the identification of corrosion type from acoustic emission signals. Int. J. Wavelets Multiresolut. Inf. Process. 2009, 7, 513–534. [Google Scholar] [CrossRef]
- Van Dijck, G.; Van Hulle, M.M. Information theoretic filters for wavelet packet coefficient selection with application to corrosion type identification from acoustic emission signals. Sensors 2011, 11, 5695–5715. [Google Scholar] [CrossRef] [PubMed]
- Van Dijck, G. Information Theoretic Approach to Feature Selection and Redundancy Assessment. PhD dissertation, Katholieke Universiteit Leuven, Leuven, Belgium, 2008. [Google Scholar]
- Huang, K.; Aviyente, S. Information-theoretic wavelet packet subband selection for texture classification. Signal Process. 2006, 86, 1410–1420. [Google Scholar] [CrossRef]
- Huang, K.; Aviyente, S. Wavelet feature selection for image classification. IEEE Trans. Image Process. 2008, 17, 1709–1720. [Google Scholar] [CrossRef] [PubMed]
- Laine, A.; Fan, J. Texture classification by wavelet packet signatures. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 1186–1191. [Google Scholar] [CrossRef]
- Khandoker, A.H.; Palaniswami, M.; Karmakar, C.K. Support vector machines for automated recognition of obstructive sleep apnea syndrome from ECG recordings. IEEE Trans. Inf. Technol. Biomed. 2009, 13, 37–48. [Google Scholar] [CrossRef] [PubMed]
- Daubechies, I. Ten Lectures on Wavelets; SIAM: Philadelphia, PA, USA, 1992. [Google Scholar]
- Tewfik, A.H.; Kim, M. Correlation structure of the discrete wavelet coefficients of fractional Brownian motion. IEEE Trans. Inf. Theory 1992, 38, 904–909. [Google Scholar] [CrossRef]
- Dijkerman, R.W.; Mazumdar, R.R. On the correlation structure of the wavelet coefficients of fractional Brownian motion. IEEE Trans. Inf. Theory 1994, 40, 1609–1612. [Google Scholar] [CrossRef]
- Koller, D.; Sahami, M. Toward optimal feature selection. In Proceedings of the Thirteenth International Conference on Machine Learning, Bari, Italy, 3–6 July 1996; pp. 284–292.
- Xing, E.P.; Jordan, M.I.; Karp, M.I. Feature selection for high-dimensional genomic microarray data. In Proceedings of the Eighteenth International Conference on Machine Learning, Williamstown, MA, USA, 28 June–1 July 2001; pp. 601–608.
- Yu, L.; Liu, H. Efficient feature selection via analysis of relevance and redundancy. J. Mach. Learn. Res. 2004, 5, 1205–1224. [Google Scholar]
- Nilsson, R.; Peña, J.M.; Björkegren, J.; Tegnér, J. Consistent feature selection for pattern recognition in polynomial time. J. Mach. Learn. Res. 2007, 8, 589–612. [Google Scholar]
- Peña, J.M.; Nilsson, R.; Björkegren, J.; Tegnér, J. Towards scalable and data efficient learning of Markov boundaries. Int. J. Approx. Reasoning 2007, 45, 211–232. [Google Scholar] [CrossRef]
- Aliferis, C.F.; Statnikov, A.; Tsamardinos, I.; Mani, S.; Koutsoukos, X.D. Local causal and Markov blanket induction for causal discovery and feature selection for classification part I: Algorithms and empirical evaluation. J. Mach. Learn. Res. 2010, 11, 171–234. [Google Scholar]
- Rodrigues de Morais, S.; Aussem, A. A novel Markov boundary based feature subset selection algorithm. Neurocomputing 2010, 73, 578–584. [Google Scholar] [CrossRef]
- Battiti, R. Using mutual information for selecting features in supervised neural net learning. IEEE Trans. Neural Netw. 1994, 5, 537–550. [Google Scholar] [CrossRef] [PubMed]
- Kwak, N.; Choi, C.H. Input feature selection for classification problems. IEEE Trans. Neural Netw. 2002, 13, 143–159. [Google Scholar] [CrossRef] [PubMed]
- Kwak, N.; Choi, C.H. Input feature selection by mutual information based on Parzen window. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 1667–1671. [Google Scholar] [CrossRef]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information: criteria of max-dependency, max-relevance and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef] [PubMed]
- Van Dijck, G.; Van Hulle, M.M. Increasing and decreasing returns and losses in mutual information feature subset selection. Entropy 2010, 12, 2144–2170. [Google Scholar] [CrossRef]
- Van Dijck, G.; Van Hulle, M.M. Speeding up feature subset selection through mutual information relevance filtering. In Knowledge Discovery in Databases: PKDD 2007, Proceedings of the 11th European Conference on Principles and Practice of Knowledge Discovery in Databases, Warsaw, Poland, 17–21, September 2007; Kok, J., Koronacki, J., Lopez de Mantaras, R., Matwin, S., Mladenic, D., Skowron, A., Eds.; Springer: Berlin, Heidelberg, Germany, 2007. [Google Scholar]Lect. Notes Comput. Sci. 2007, 4702, 277–287.
- Van Dijck, G.; Van Hulle, M.M. Speeding up the wrapper feature subset selection in regression by mutual information relevance and redundancy analysis. In Artificial Neural Networks: ICANN 2006, Proceedings of the 16th International Conference on Artificial Neural Networks, Athens, Greece, 10–14 September 2006; Kollias, S.D., Stafylopatis, A., Duch, W., Oja, E., Eds.; Springer: Berlin, Heidelberg, Germany, 2006. [Google Scholar]Lect. Notes Comput. Sci. 2006, 4131, 31–40.
- Lewis II, P.M. The characteristic selection problem in recognition systems. IEEE Trans. Inf. Theory 1962, 8, 171–178. [Google Scholar] [CrossRef]
- Meyer, P.; Schretter, C.; Bontempi, G. Information-theoretic feature selection in micro-array data using variable complementarity. IEEE J. Sel. Top. Sign. Proces. 2008, 2, 261–274. [Google Scholar] [CrossRef]
- John, G.H.; Kohavi, R.; Pfleger, H. Irrelevant feature and the subset selection problem. In Proceedings of the Eleventh International Conference on Machine Learning, New Brunswick, NJ, USA, 10–13 July 1994; pp. 121–129.
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Zheng, Y.; Kwoh, C.K. A feature subset selection method based on high-dimensional mutual information. Entropy 2011, 13, 860–901. [Google Scholar] [CrossRef]
- Knijnenburg, T.A.; Reinders, M.J.T.; Wessels, L.F.A. Artifacts of Markov blanket filtering based on discretized features in small sample size applications. Pattern Recognit. Lett. 2006, 27, 709–714. [Google Scholar] [CrossRef]
- Kovalevsky, V.A. The problem of character recognition from the point of view of mathematical statistics. In Character Readers and Pattern Recognition; Kovalevsky, V.A., Ed.; Spartan: New York, NY, USA, 1968. [Google Scholar]
- Feder, M.; Merhav, N. Relations between entropy and error probability. IEEE Trans. Inf. Theory 1994, 40, 259–266. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Raudys, S.; Jain, A. Small sample size effects in statistical pattern recognition: Recommendations for practitioners. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 252–264. [Google Scholar] [CrossRef]
- Raudys, S. On dimensionality, sample size and classification error of nonparametric linear classification algorithms. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 667–671. [Google Scholar] [CrossRef]
- Raudys, S. Statistical and Neural Classifiers: An Integrated Approach to Design; Springer-Verlag: London, UK, 2001. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector network. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. 2001. Software available online: http://www.csie.ntu.edu.tw∼cjlin/libsvm (accessed on 18 July 2011).
- Kecman, V. Learning and Soft Computing, Support Vector Machines, Neural Networks and Fuzzy Logic Models; The MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Support Vector Machines: Theory and Application; Wang, L.P. (Ed.) Springer: Berlin, Germany, 2005.
- Sloin, A.; Burshtein, D. Support vector machine training for improved hidden markov modeling. IEEE Trans. Signal Process. 2008, 56, 172–188. [Google Scholar] [CrossRef]
- Wang, L.P.; Fu, X.J. Data Mining with Computational Intelligence; Springer: Berlin, Germany, 2005. [Google Scholar]
- Keogh, E. UCR time series classification/clustering page. Training and testing data sets: Available online: http://www.cs.ucr.edu/ eamonn/time_series_data/ (accessed on 18 July 2011).
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Van Dijck, G.; Van Hulle, M.M. Joint Markov Blankets in Feature Sets Extracted from Wavelet Packet Decompositions. Entropy 2011, 13, 1403-1424. https://doi.org/10.3390/e13071403
Van Dijck G, Van Hulle MM. Joint Markov Blankets in Feature Sets Extracted from Wavelet Packet Decompositions. Entropy. 2011; 13(7):1403-1424. https://doi.org/10.3390/e13071403
Chicago/Turabian StyleVan Dijck, Gert, and Marc M. Van Hulle. 2011. "Joint Markov Blankets in Feature Sets Extracted from Wavelet Packet Decompositions" Entropy 13, no. 7: 1403-1424. https://doi.org/10.3390/e13071403



