Control Parameters for Boundary-Layer Instabilities in Unsteady Shock Interactions
Abstract
:1. Introduction
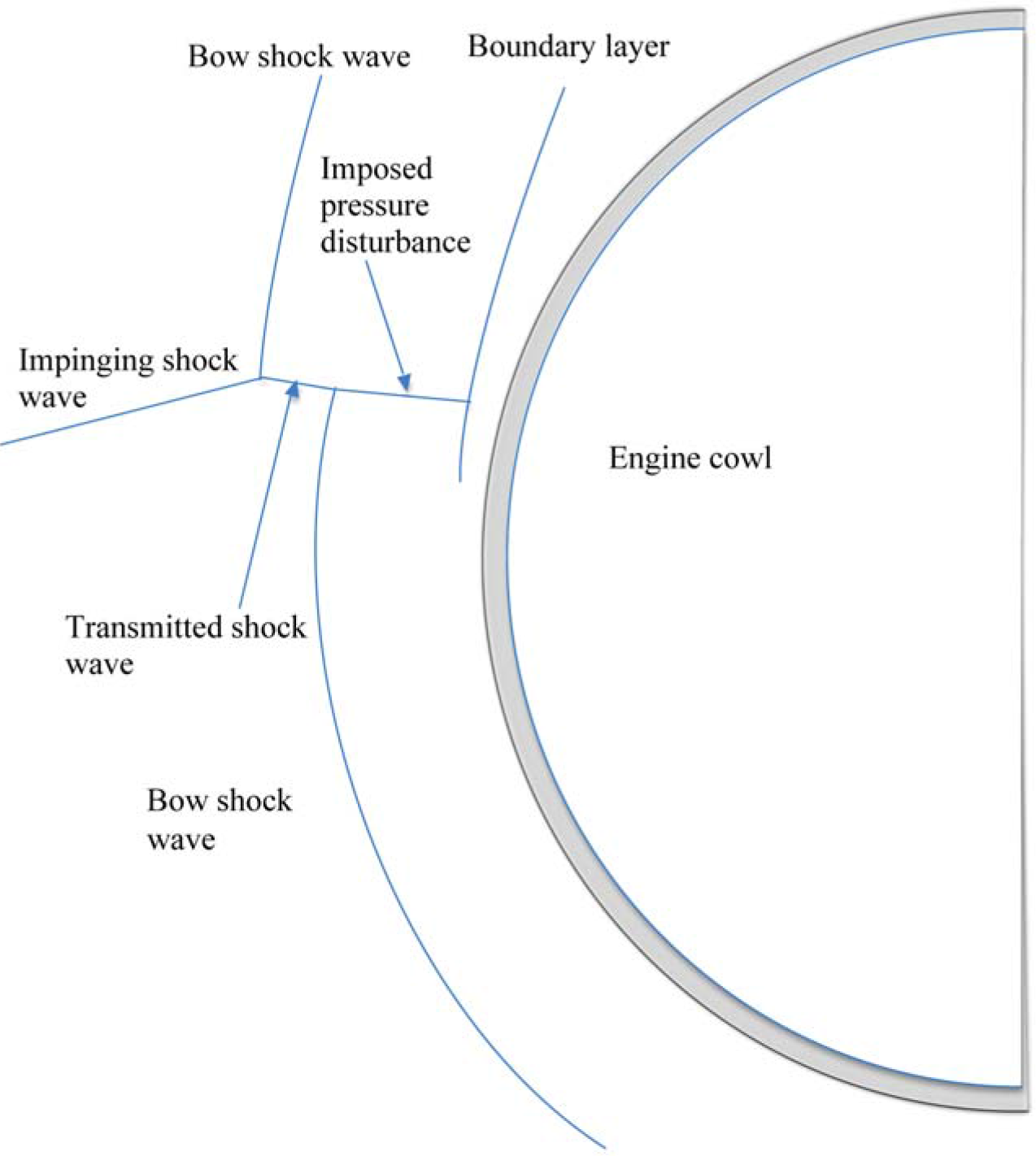
2. Supersonic Flight Environment
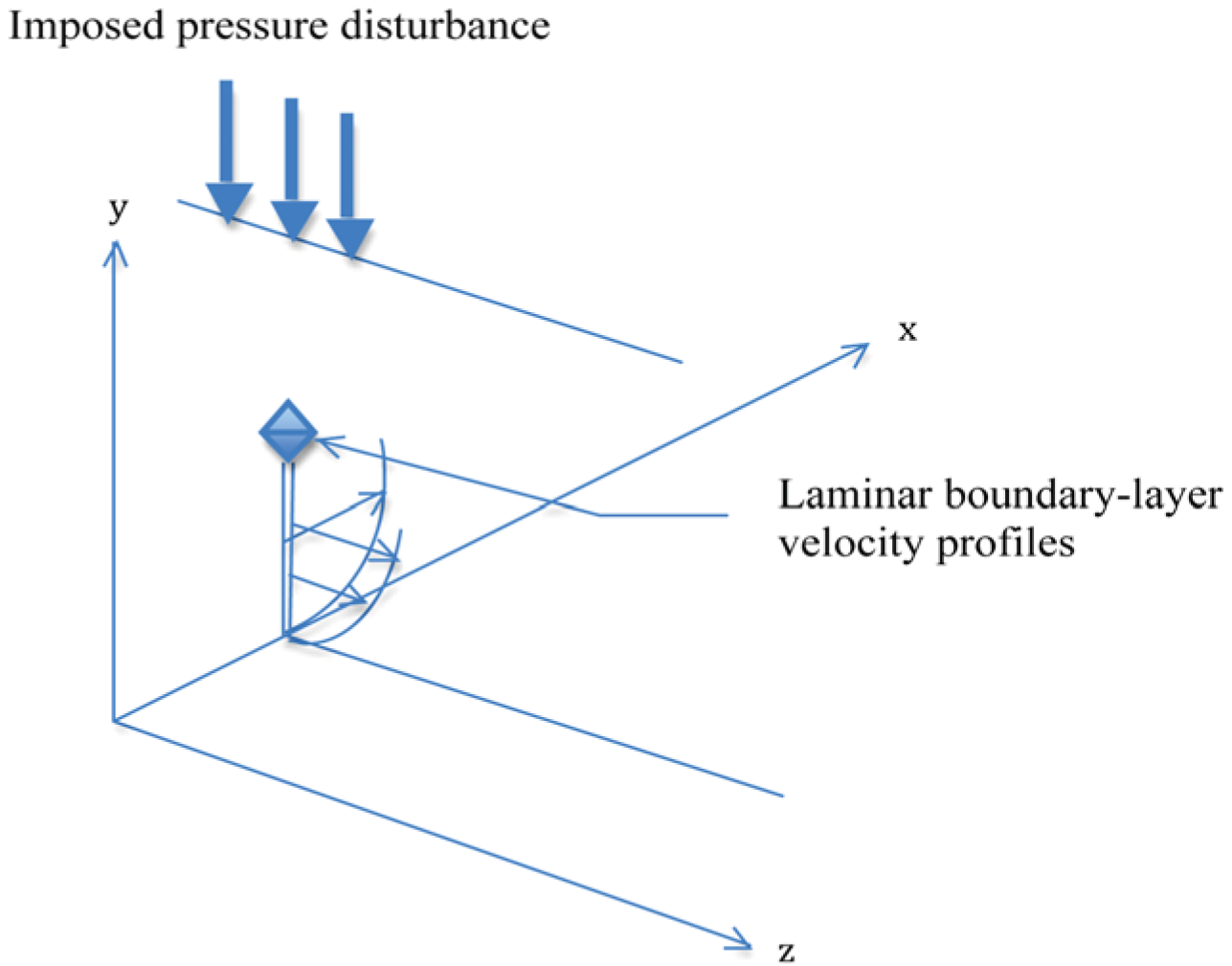
3. Boundary-Layer Flow Environment
3.1. Computational Model for the Boundary-Layer Flow
| j | η | ||||
|---|---|---|---|---|---|
| 1 | 0.0000 | ||||
| 2 | 0.2000 | −0.3953 | 87.9648 | 0.0018 | 0.3953 |
| 3 | 0.4000 | −0.7921 | 88.1166 | 0.0098 | 0.7921 |
| 4 | 0.6000 | −1.1855 | 87.9006 | 0.0231 | 1.1855 |
| 5 | 0.8010 | −1.5686 | 87.2045 | 0.0415 | 1.5686 |
| 6 | 1.0010 | −1.9325 | 85.9288 | 0.0647 | 1.9325 |
| 7 | 1.2020 | −2.2673 | 83.9931 | 0.0919 | 2.2673 |
| 8 | 1.4020 | −2.5624 | 81.3431 | 0.1223 | 2.5624 |
| 9 | 1.6030 | −2.8073 | 77.9565 | 0.1548 | 2.8073 |
| 10 | 1.8040 | −2.9925 | 73.8486 | 0.1881 | 2.9925 |
| 11 | 2.0050 | −3.1108 | 69.0742 | 0.2207 | 3.1108 |
| 12 | 2.2060 | −3.1578 | 63.7273 | 0.2512 | 3.1578 |
| 13 | 2.4070 | −3.1326 | 57.9367 | 0.2784 | 3.1326 |
| 14 | 2.6080 | −3.0384 | 51.8577 | 0.3010 | 3.0384 |
| 15 | 2.8090 | −2.8818 | 45.6616 | 0.3183 | 2.8818 |
| 16 | 3.0110 | −2.6733 | 39.5230 | 0.3298 | 2.6733 |
| 17 | 3.2120 | −2.4252 | 33.6067 | 0.3356 | 2.4252 |
| 18 | 3.4140 | −2.1518 | 28.0563 | 0.3360 | 2.1518 |
| 19 | 3.6150 | −1.8670 | 22.9850 | 0.3317 | 1.8670 |
| 20 | 3.8170 | −1.5841 | 18.4706 | 0.3238 | 1.5841 |
| 21 | 4.0190 | −1.3142 | 14.5540 | 0.3132 | 1.3142 |
| 22 | 4.2210 | −1.0661 | 11.2411 | 0.3010 | 1.0661 |
| 23 | 4.4230 | −0.8455 | 8.5083 | 0.2883 | 0.8455 |
| 24 | 4.6250 | −0.6557 | 6.3093 | 0.2758 | 0.6557 |
| 25 | 4.8280 | −0.4971 | 4.5829 | 0.2642 | 0.4971 |
| 26 | 5.0300 | −0.3685 | 3.2603 | 0.2539 | 0.3685 |
| 27 | 5.2330 | −0.2670 | 2.2711 | 0.2451 | 0.2670 |
| 28 | 5.4350 | −0.1891 | 1.5489 | 0.2378 | 0.1891 |
| 29 | 5.6380 | −0.1310 | 1.0341 | 0.2320 | 0.1310 |
| 30 | 5.8410 | −0.0887 | 0.6757 | 0.2275 | 0.0887 |
| 31 | 6.0440 | −0.0587 | 0.4321 | 0.2242 | 0.0587 |
| 32 | 6.2470 | −0.0380 | 0.2704 | 0.2218 | 0.0380 |
| 33 | 6.4500 | −0.0240 | 0.1656 | 0.2200 | 0.0240 |
| 34 | 6.6530 | −0.0148 | 0.0992 | 0.2188 | 0.0148 |
| 35 | 6.8560 | −0.0090 | 0.0581 | 0.2180 | 0.0090 |
| 36 | 7.0600 | −0.0053 | 0.0333 | 0.2175 | 0.0053 |
| 37 | 7.2630 | −0.0030 | 0.0187 | 0.2172 | 0.0030 |
| 38 | 7.4670 | −0.0017 | 0.0102 | 0.2170 | 0.0017 |
| 39 | 7.6710 | −0.0009 | 0.0055 | 0.2168 | 0.0009 |
| 40 | 7.8750 | −0.0005 | 0.0029 | 0.2168 | 0.0005 |
| 41 | 8.0780 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| j | η | ||||
|---|---|---|---|---|---|
| 1 | 0.0000 | ||||
| 2 | 0.2000 | −2.2089 | 15.1271 | −0.1613 | 2.2089 |
| 3 | 0.4000 | −4.3987 | 15.0620 | −0.6423 | 4.3987 |
| 4 | 0.6000 | −6.5437 | 14.9379 | −1.4333 | 6.5437 |
| 5 | 0.8000 | −8.6074 | 14.7368 | −2.5137 | 8.6074 |
| 6 | 1.0000 | −10.5449 | 14.4432 | −3.8494 | 10.5449 |
| 7 | 1.2000 | −12.3050 | 14.0449 | −5.3903 | 12.3050 |
| 8 | 1.4000 | −13.8338 | 13.5342 | −7.0700 | 13.8338 |
| 9 | 1.6000 | −15.0793 | 12.9086 | −8.8075 | 15.0793 |
| 10 | 1.8000 | −15.9963 | 12.1721 | −10.5110 | 15.9963 |
| 11 | 2.0000 | −16.5510 | 11.3348 | −12.0839 | 16.5510 |
| 12 | 2.2000 | −16.7256 | 10.4130 | −13.4325 | 16.7256 |
| 13 | 2.4000 | −16.5210 | 9.4285 | −14.4744 | 16.5210 |
| 14 | 2.6000 | −15.9583 | 8.4068 | −15.1465 | 15.9583 |
| 15 | 2.8000 | −15.0779 | 7.3757 | −15.4117 | 15.0779 |
| 16 | 3.0000 | −13.9362 | 6.3627 | −15.2622 | 13.9362 |
| 17 | 3.2000 | −12.6013 | 5.3937 | −14.7203 | 12.6013 |
| 18 | 3.4000 | −11.1469 | 4.4905 | −13.8352 | 11.1469 |
| 19 | 3.6000 | −9.6461 | 3.6700 | −12.6766 | 9.6461 |
| 20 | 3.8000 | −8.1657 | 2.9433 | −11.3274 | 8.1657 |
| 21 | 4.0000 | −6.7621 | 2.3155 | −9.8740 | 6.7621 |
| 22 | 4.2000 | −5.4778 | 1.7864 | −8.3986 | 5.4778 |
| 23 | 4.4000 | −4.3408 | 1.3512 | −6.9722 | 4.3408 |
| 24 | 4.6000 | −3.3648 | 1.0019 | −5.6503 | 3.3648 |
| 25 | 4.8000 | −2.5515 | 0.7281 | −4.4709 | 2.5515 |
| 26 | 5.0000 | −1.8927 | 0.5185 | −3.4547 | 1.8927 |
| 27 | 5.2000 | −1.3735 | 0.3618 | −2.6072 | 1.3735 |
| 28 | 5.4000 | −0.9750 | 0.2473 | −1.9220 | 0.9750 |
| 29 | 5.6000 | −0.6771 | 0.1656 | −1.3842 | 0.6771 |
| 30 | 5.8000 | −0.4600 | 0.1086 | −0.9739 | 0.4600 |
| 31 | 6.0000 | −0.3057 | 0.0698 | −0.6695 | 0.3057 |
| 32 | 6.2000 | −0.1987 | 0.0439 | −0.4497 | 0.1987 |
| 33 | 6.4000 | −0.1263 | 0.0270 | −0.2952 | 0.1263 |
| 34 | 6.6000 | −0.0786 | 0.0163 | −0.1894 | 0.0786 |
| 35 | 6.8000 | −0.0478 | 0.0096 | −0.1187 | 0.0478 |
| 36 | 7.0000 | −0.0284 | 0.0056 | −0.0727 | 0.0284 |
| 37 | 7.2000 | −0.0165 | 0.0031 | −0.0435 | 0.0165 |
| 38 | 7.4000 | −0.0094 | 0.0017 | −0.0254 | 0.0094 |
| 39 | 7.6000 | −0.0052 | 0.0009 | −0.0146 | 0.0052 |
| 40 | 7.8000 | −0.0029 | 0.0005 | −0.0081 | 0.0029 |
| 41 | 8.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
4. Mathematical Model of the Flow Instability
4.1. Transformation of the Townsend Equations
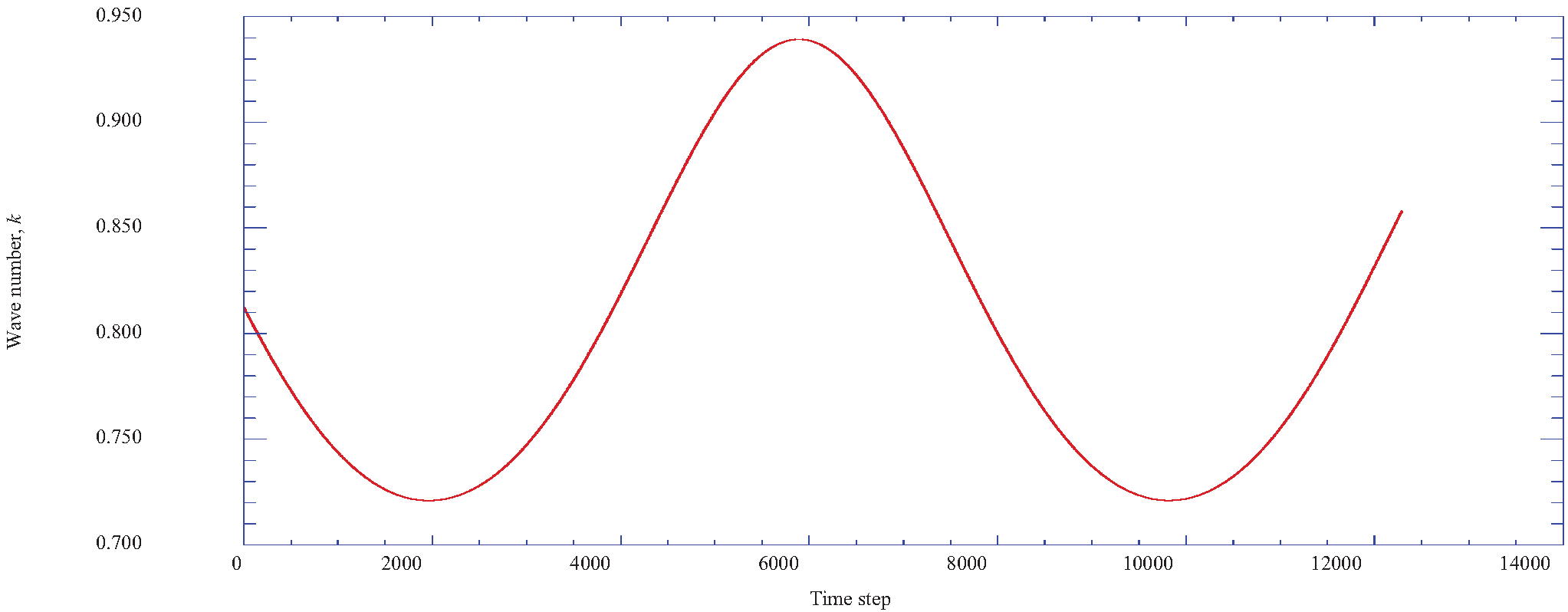
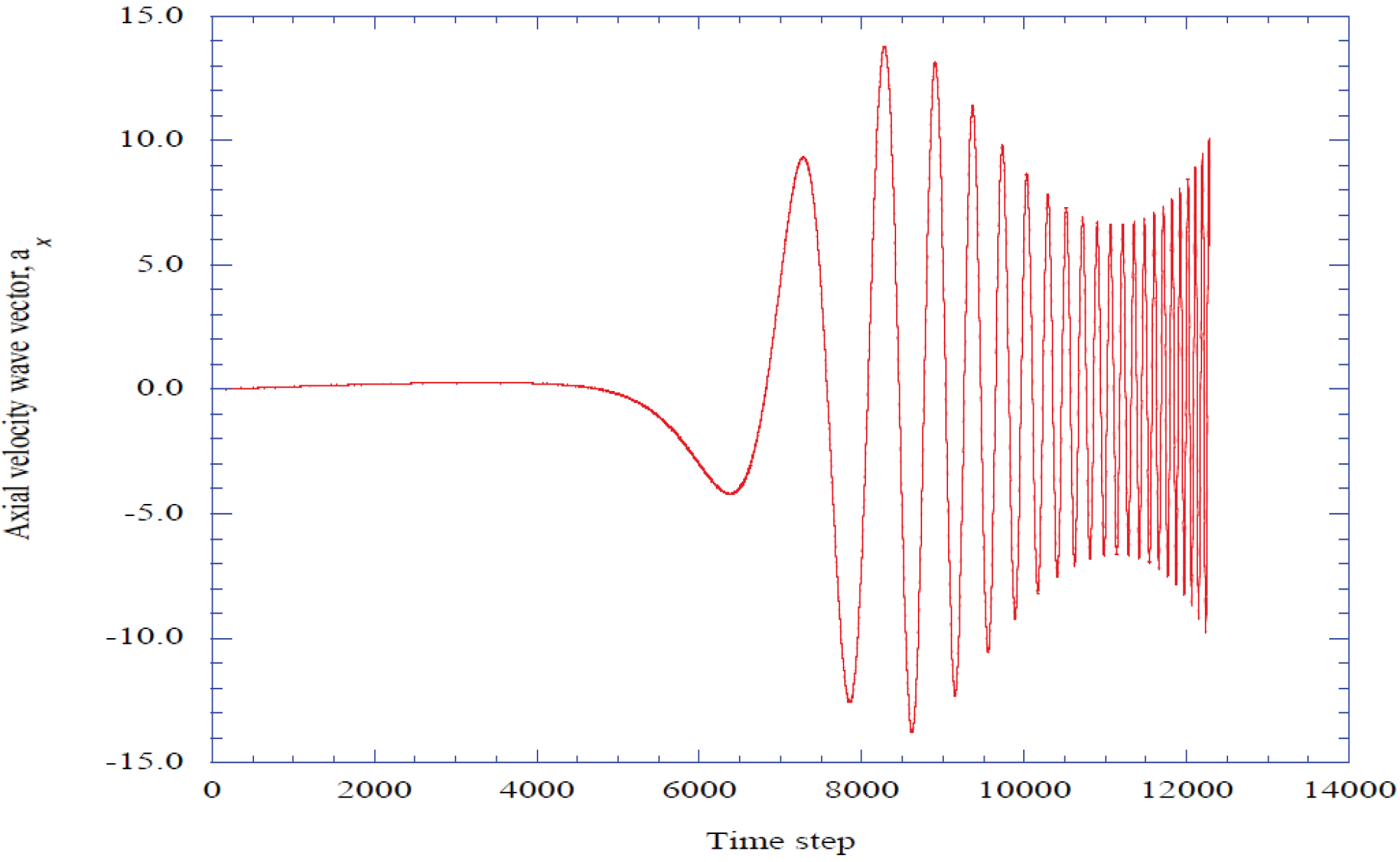
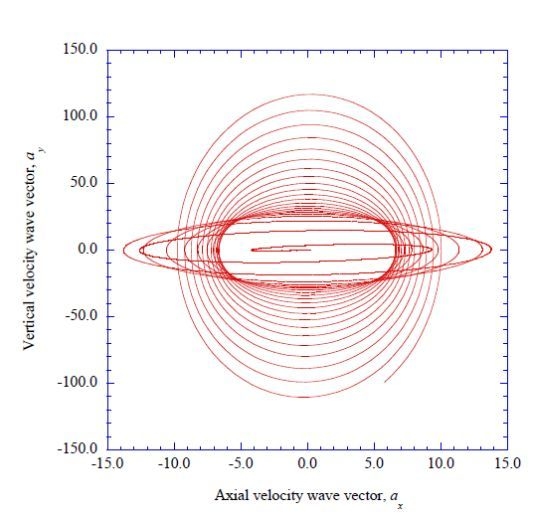
4.2. The Prediction of Spectral Entropy Rates from the Deterministic Results
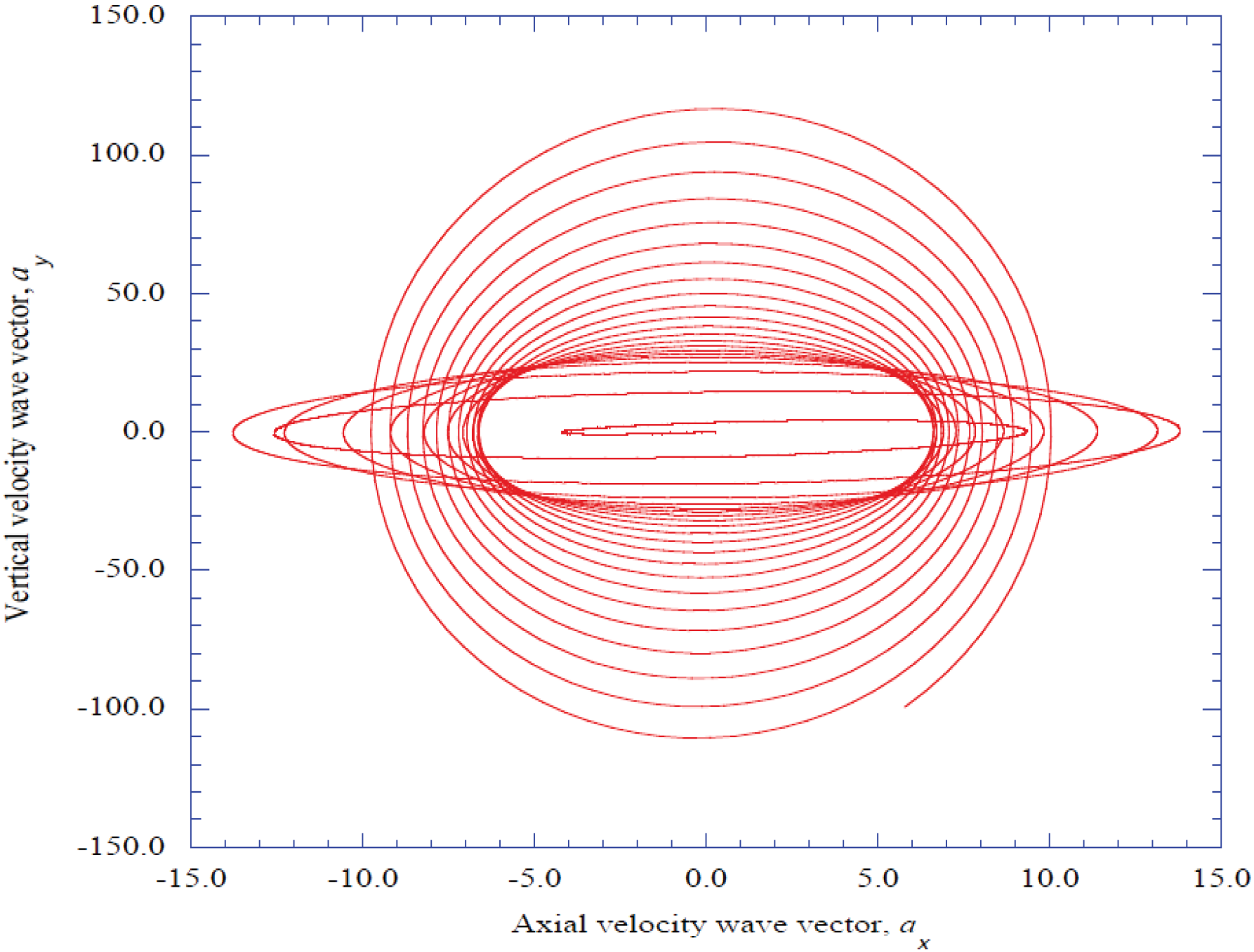
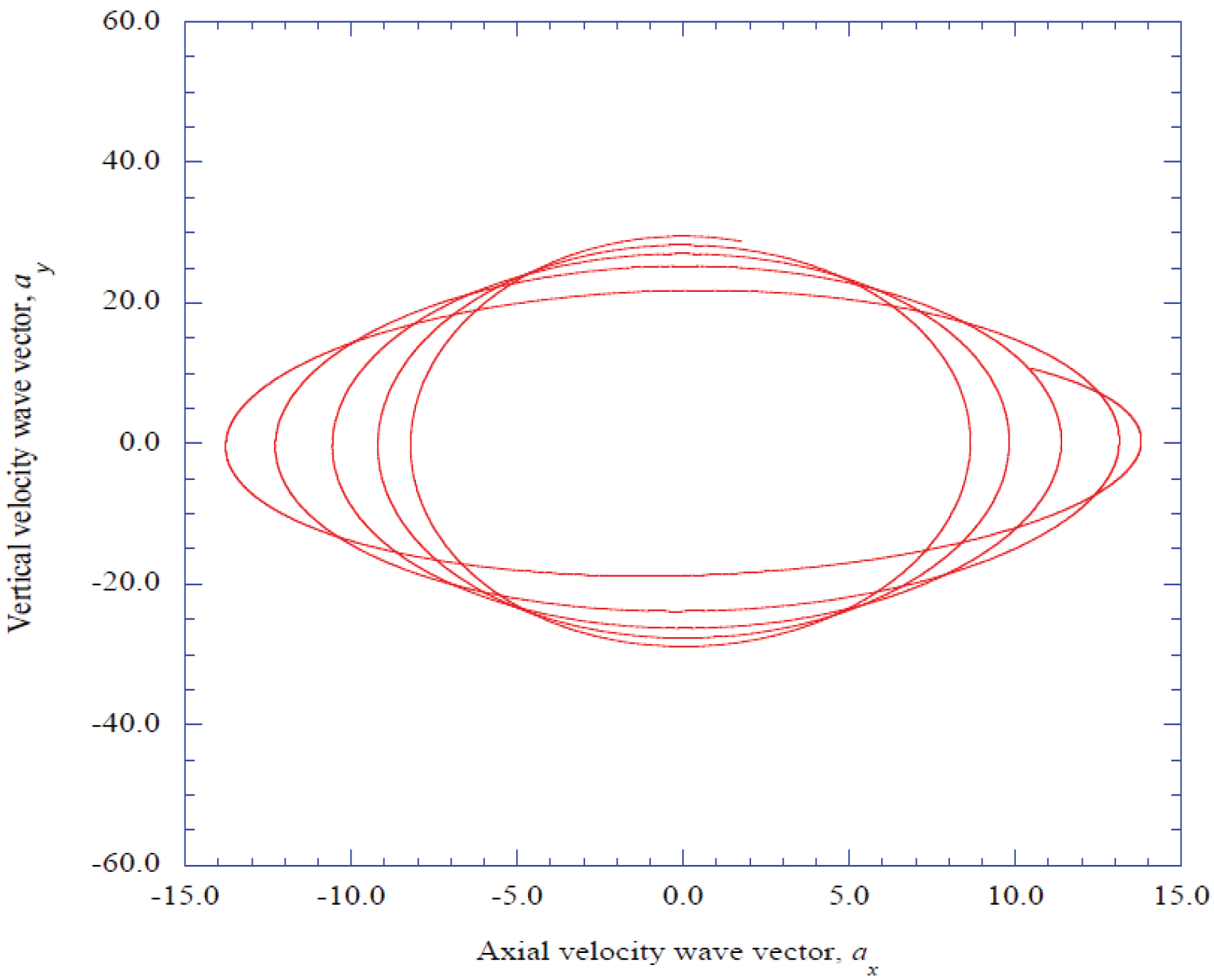
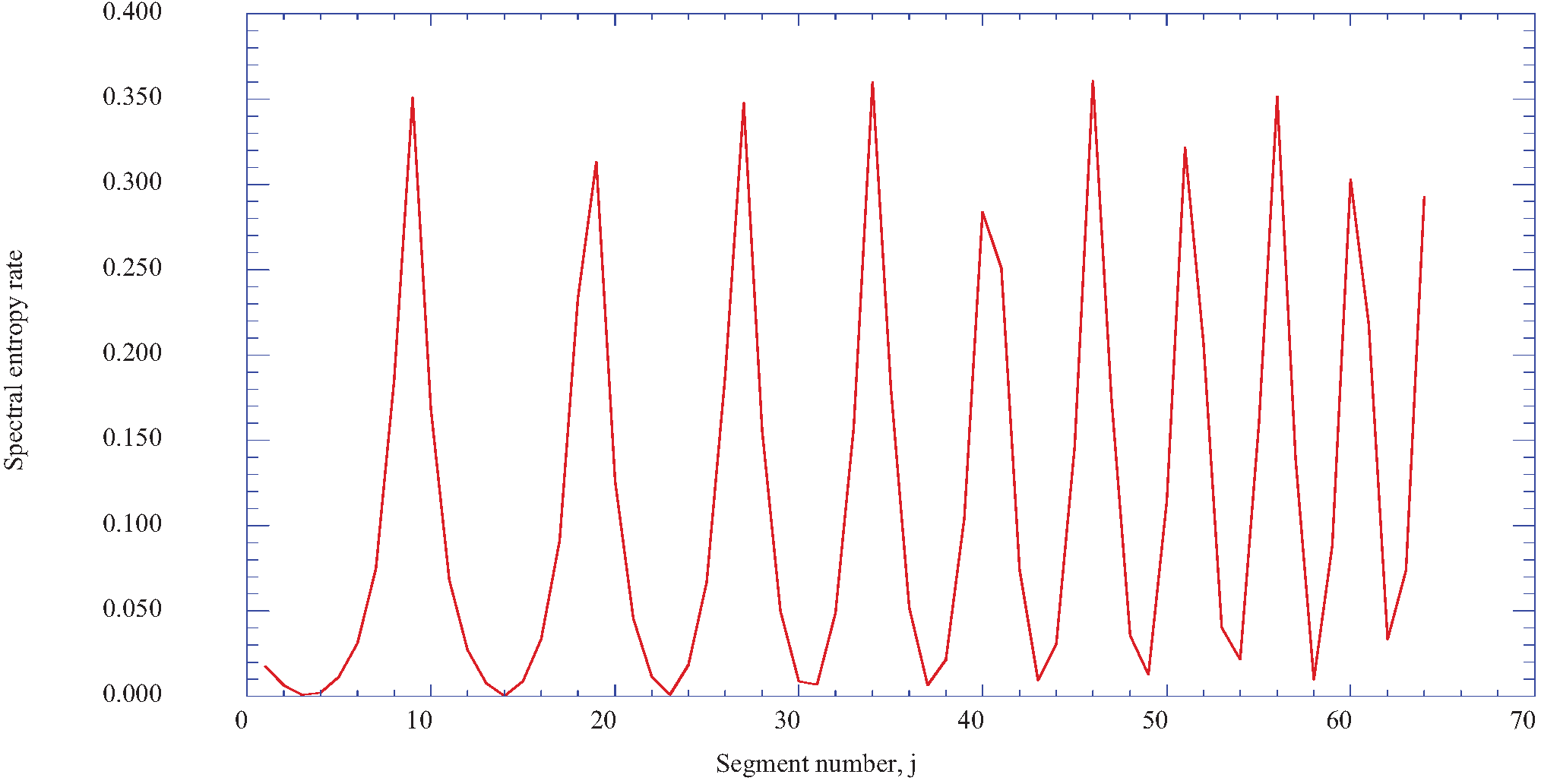
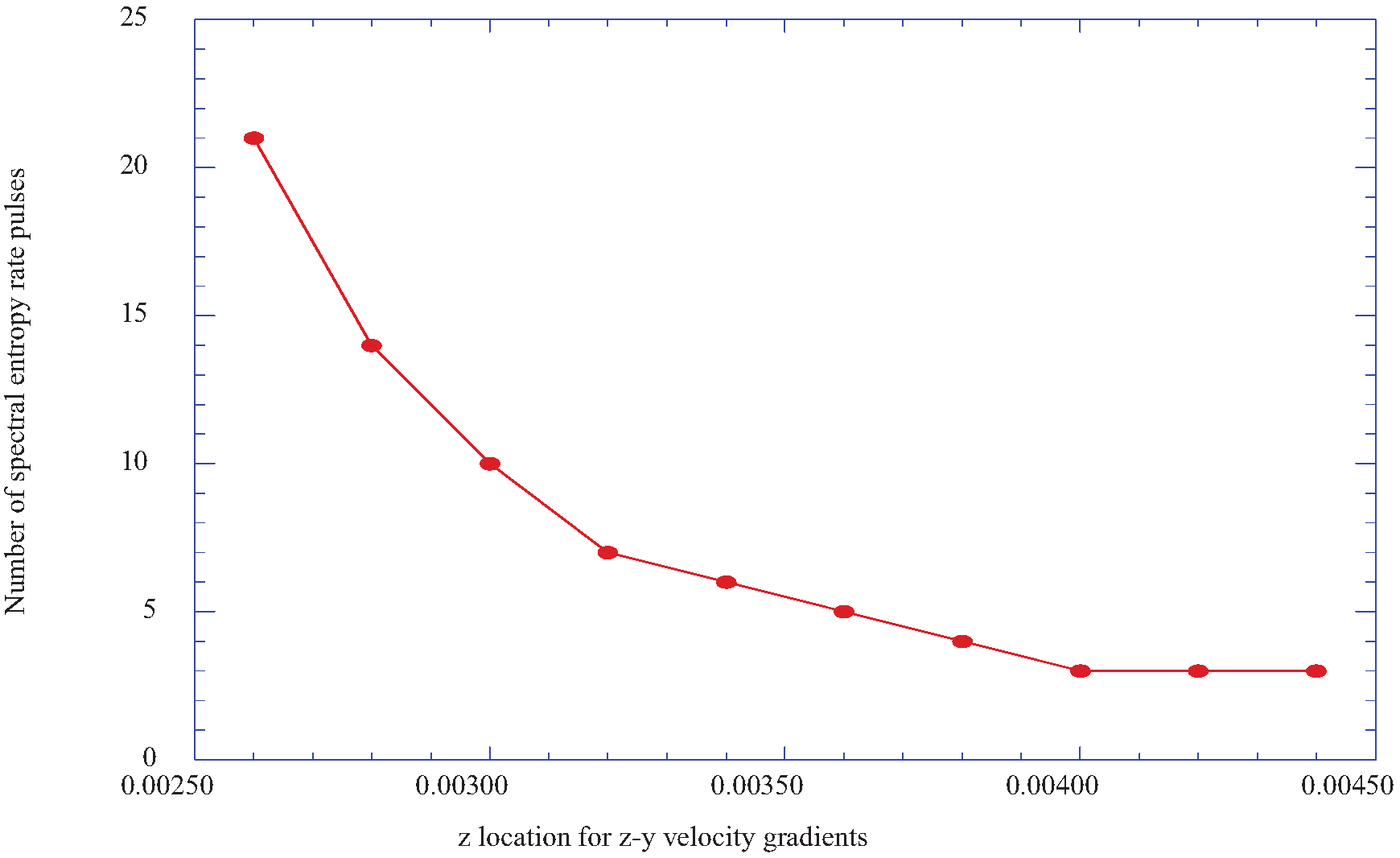
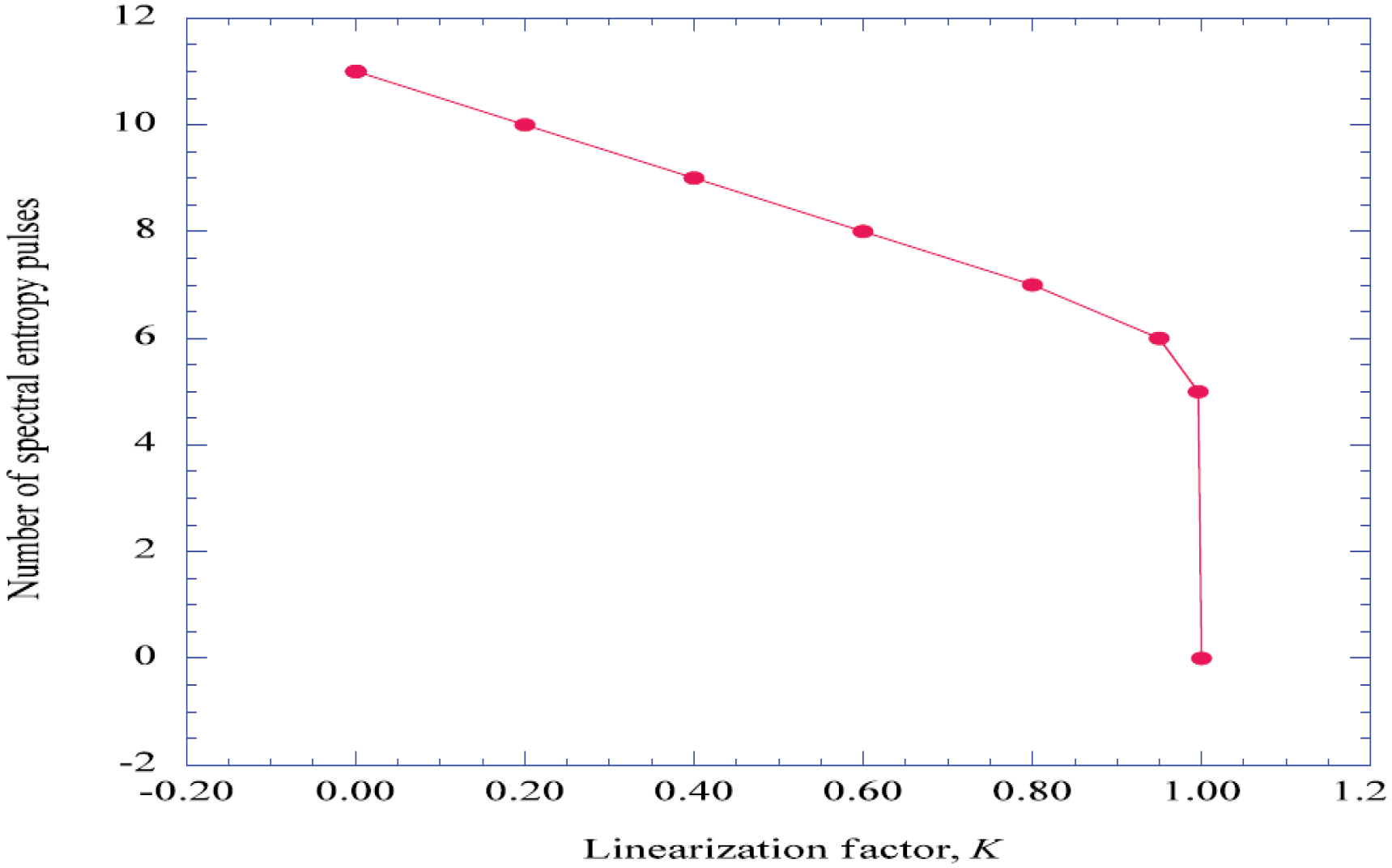
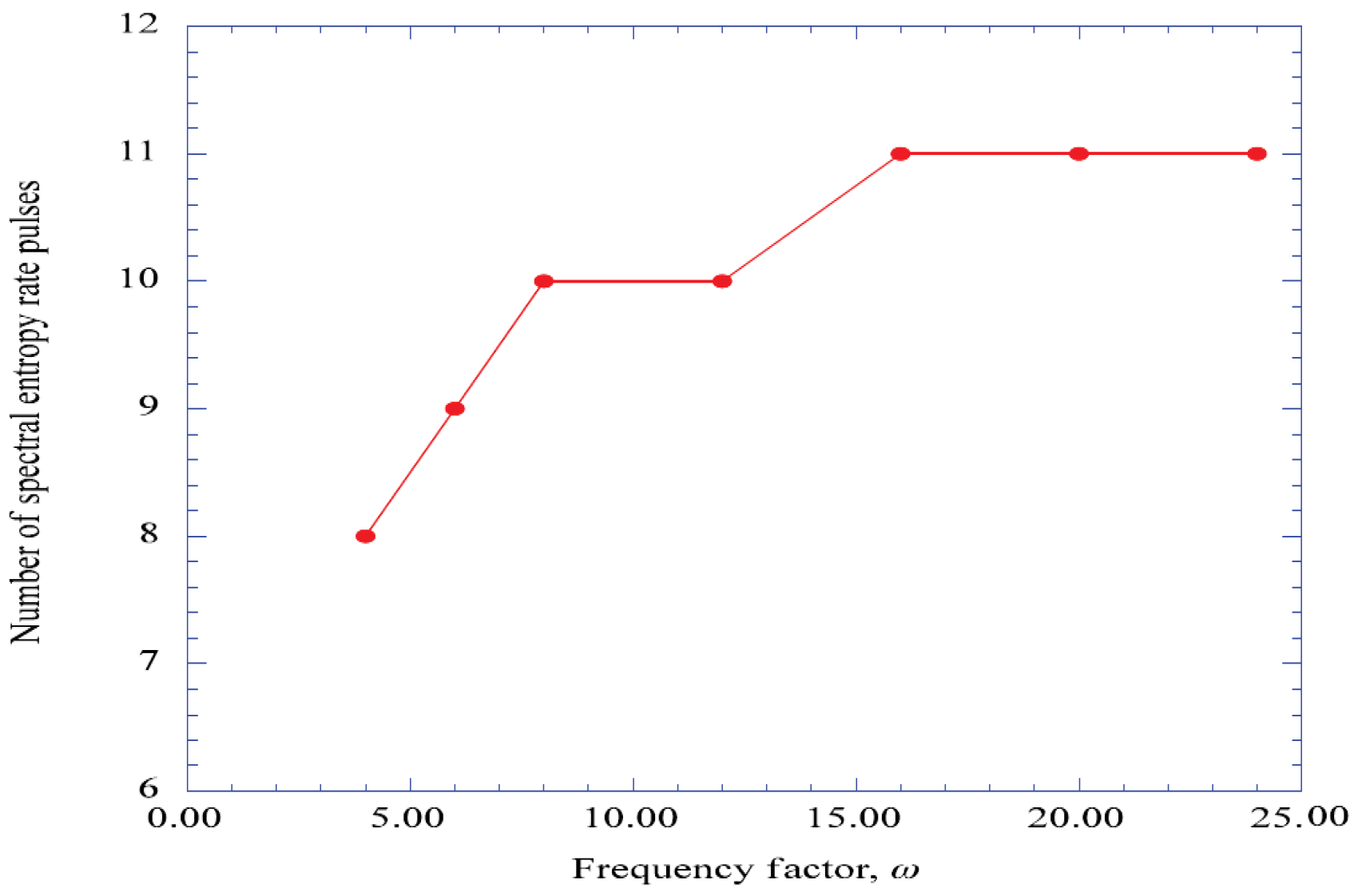
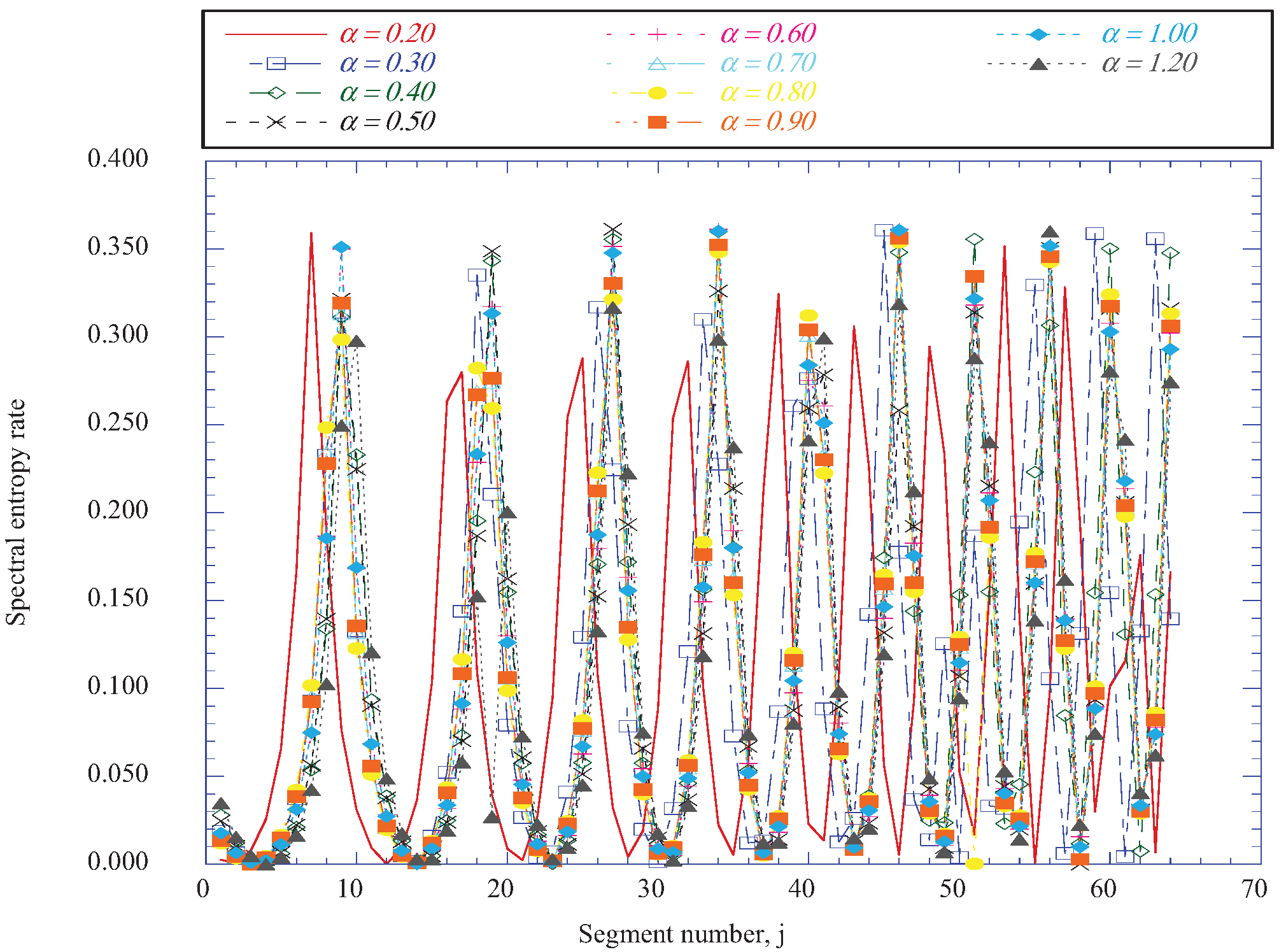

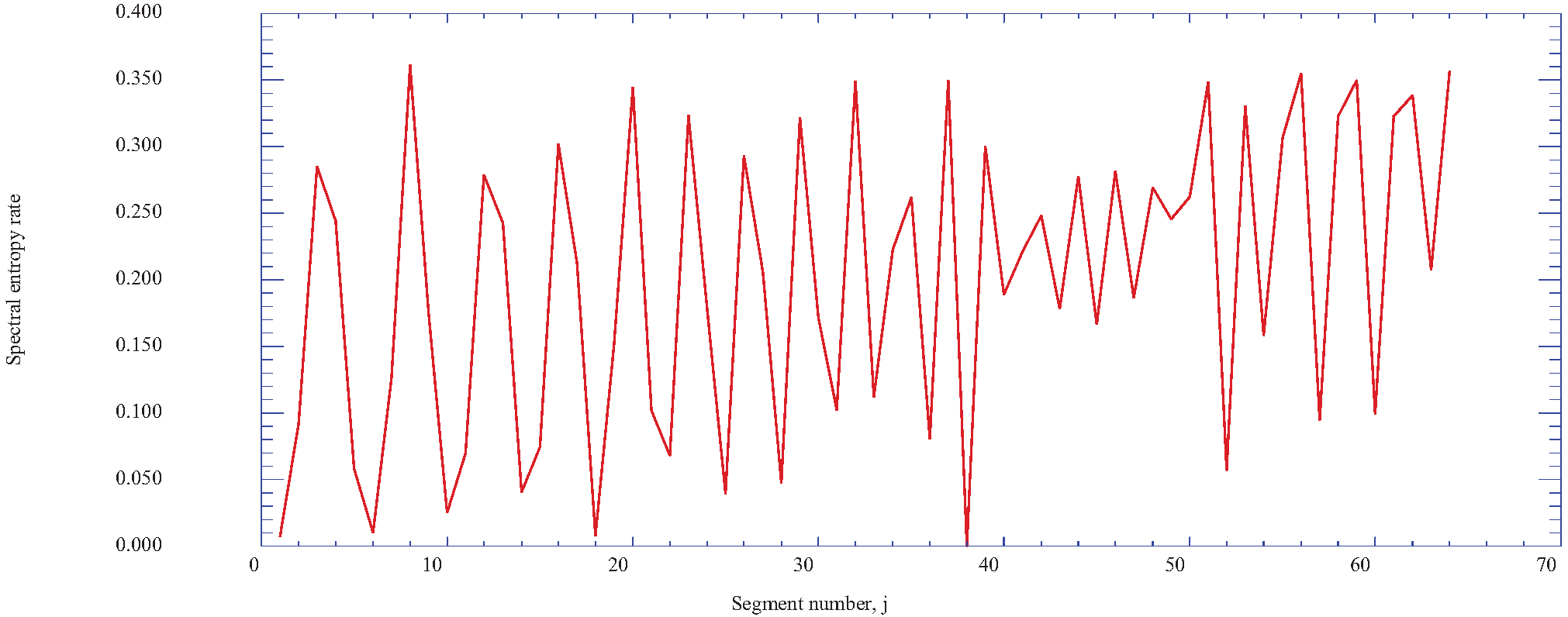
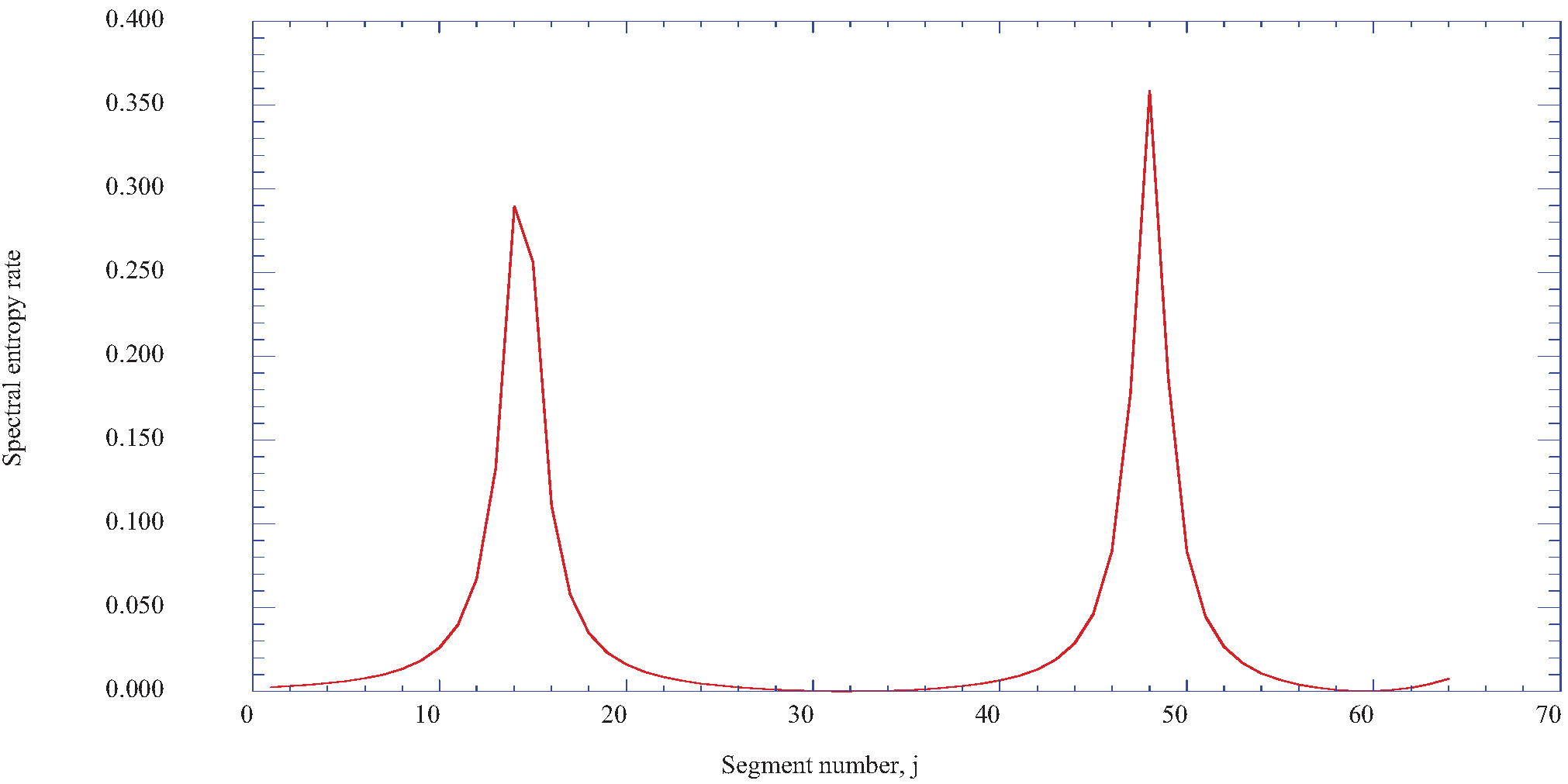

6. Discussion
7. Conclusions
Nomenclature
| ai | Fluctuating i-th component of velocity wave vector |
| Cpf | Specific heat at constant pressure for the gas mixture |
| f | Dimensionless stream function |
| f’ | First derivative of f with respect to η |
| f’’ | Second derivative of f with respect to η |
| fr | Sum of the squares of the fluctuating axial and vertical velocity wave vectors |
| F | Time-dependent perturbation factor |
| j | Vertical station number in the boundary layer computations |
| j | Time data segment |
| k | Time-dependent wave number magnitude |
| ki | Fluctuating i-th wave number of Fourier expansion |
| K | Adjustable linearization weight factor |
| m | Pressure gradient parameter |
| M1 | Flight Mach number |
| M2 | Mach number downstream of the bow shock wave |
| nx | Axial station number in the boundary layer computations |
| p | Hydrostatic pressure |
| p1 | Static pressure ahead of the bow shock wave |
| p2 | Static pressure behind the bow shock wave |
| Pr | Power spectral density of the r-th spectral segment |
| Prf | Prandtl number of the gas mixture |
| Rc | Boundary-layer recovery factor |
| sj_spent | Spectral entropy rate over the j-th time data segment |
| t | Time |
| t1 | Static temperature ahead of the bow shock wave |
| t2 | Static temperature behind the bow shock wave |
| Taw | Adiabatic wall temperature |
| u | Axial boundary layer velocity |
| ue | Axial velocity at the outer edge of the boundary layer |
| ui | Fluctuating i-component of velocity instability |
| Ui | Mean velocity in the i-direction |
| v | Vertical boundary layer velocity |
| Vy | Mean vertical velocity in the x-y plane |
| Vz | Mean vertical velocity in the z-y plane |
| w | Span wise boundary layer velocity |
| W | Mean velocity in the span wise direction |
| x | Axial distance |
| xi | i-th direction |
| xj | j-th direction |
| y | Vertical distance |
| z | Span wise distance |
| Greek Letters | |
| α | Amplification factor |
| γ | Ratio of specific heats for air |
| δ | Boundary-layer thickness |
| δlm | Kronecker delta |
| η | Transformed vertical parameter |
| κf | Thermal conductivity of the gas mixture |
| μ | Dynamic viscosity of air |
| μf | Dynamic viscosity of the gas mixture |
| ν | Kinematic viscosity of air |
| ω | Frequency factor |
| Ψ | Transformed stream function |
| Subscripts | |
| i, j, l, m | Tensor indices |
| r | The r-th index in the j-th time series data segment |
| x | Component in the x-direction |
| y | Component in the y-direction |
| z | Component in the z-direction |
Acknowledgements
References
- Klimontovich, Y.L.; Bonitz, M. Definition of the degree of order in selforganization processes. Annalen der Physik 1988, 7, 340–352. [Google Scholar] [CrossRef]
- Kapitaniak, T. Controlling Chaos; Academic Press Inc.: San Diego, CA, USA, 1996. [Google Scholar]
- Pyragas, K. Continuous control of chaos by self-controlling feedback. Phys. Lett. A 1990, 170, 421–427. [Google Scholar] [CrossRef]
- Pyragas, K. Predictable chaos in slightly perturbed unpredictable chaotic systems. Phys. Lett. A 1993, 181, 203–210. [Google Scholar] [CrossRef]
- Isaacson, L.K. Spectral entropy in a boundary-layer flow. Entropy 2011, 13, 402–421. [Google Scholar] [CrossRef]
- Panaras, A.G.; Drikakis, D. High-speed unsteady flows around spiked-blunt bodies. J. Fluid Mech. 2009, 63, 69–96. [Google Scholar] [CrossRef]
- Drikakis, D.; Rider, W. High-Resolution Methods for Incompressible and Low-Speed Flows; Springer-Verlag: Berlin, Germany, 2005. [Google Scholar]
- Lind, C.A.; Lewis, M.J. Computational analysis of the unsteady type IV shock interaction of blunt body flows. J. Propul. Power 1996, 12, 127–133. [Google Scholar] [CrossRef]
- Lind, C.A. Effect of geometry on the unsteady type IV shock interaction. J. Aircraft 1997, 34, 64–71. [Google Scholar] [CrossRef]
- Townsend, A.A. The Structure of Turbulent Shear Flow, 2nd ed.; Cambridge University Press: Cambridge, UK, 1976; pp. 45–49. [Google Scholar]
- Chen, C.H. Digital Waveform Processing and Recognition; CRC Press, Inc.: Boca Raton, FL, USA, 1982; pp. 131–158. [Google Scholar]
- Press, W.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C: The Art of Scientific Computing, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992; pp. 572–575. [Google Scholar]
- Powell, G.E.; Percival, I.C. A spectral entropy method for distinguishing regular and irregular motions for Hamiltonian systems. J. Phys. Math. Gen. 1979, 12, 2053–2071. [Google Scholar] [CrossRef]
- Anderson, J.D., Jr. Hypersonic and High-Temperature Gas Dynamics, 2nd ed.; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 2006; pp. 395–406. [Google Scholar]
- Ben-Dor, G. Shock Wave Reflection Phenomena, 2nd ed.; Springer-Verlag: Berlin, Germany, 2007. [Google Scholar]
- Zucrow, M.J.; Hoffman, J.D. Gas Dynamics; John Wiley & Sons, Inc.: New York, NY, USA, 1976; Volume 1, pp. 708–709. [Google Scholar]
- Zucrow, M.J.; Hoffman, J.D. Gas Dynamics; John Wiley & Sons, Inc.: New York, NY, USA, 1976; Volume 1, pp. 335–349. [Google Scholar]
- Truitt, R.W. Fundamentals of Aerodynamic Heating; Ronald Press Company: New York, NY, USA, 1960; pp. 9–20. [Google Scholar]
- Heywood, J.B. Internal Combustion Engine Fundamentals; McGraw-Hill Book Company: New York, NY, USA, 1988; pp. 130–135. [Google Scholar]
- Zucrow, M.J.; Hoffman, J.D. Gas Dynamics; John Wiley & Sons, Inc.: New York, NY, USA, 1976; Volume 1, pp. 20–23. [Google Scholar]
- Mills, A.F. Heat Transfer; Richard D. Irwin, Inc.: Boston, MA, USA, 1992; pp. 824–827. [Google Scholar]
- Dorrance, W.H. Viscous Hypersonic Flow; McGraw-Hill Book Company, Inc.: New York, NY, USA, 1962; pp. 276–315. [Google Scholar]
- Cebeci, T.; Bradshaw, P. Momentum Transfer in Boundary Layers; Hemisphere: Washington, DC, USA, 1977. [Google Scholar]
- Hansen, A.G. Similarity Analyses of Boundary Value Problems in Engineering; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1964; pp. 86–92. [Google Scholar]
- Durbin, P; Zaki, T. Continuous mode transition. In Transition and Turbulence Control; Gad-el-Hak, M., Tsai, H.M., Eds.; World Scientific Pub. Co.: Singapore, 2006; pp. 87–106. [Google Scholar]
- Andersson, P.; Berggren, M.; Henningson, D.S. Optimal disturbances and bypass transition in boundary layers. Phys. Fluids 1999, 11, 134–150. [Google Scholar] [CrossRef]
- Corbett, P.; Bottaro, A. Optimal perturbations for boundary layers subject to stream-wise pressure gradient. Phys. Fluids 2000, 12, 120–130. [Google Scholar] [CrossRef]
- Brandt, L.; de Lange, H.C. Streak interactions and breakdown in boundary layer flows. Phys. Fluids 2008, 20, 024107. [Google Scholar] [CrossRef]
- Hoepffner, J.; Brandt, L. Stochastic approach to the receptivity problem applied to bypass transition in boundary layers. Phys. Fluids 2008, 20, 024108. [Google Scholar] [CrossRef]
- Schlatter, P.; Brandt, L.; de Lange, H.C.; Henningson, D.S. On streak breakdown in bypass transition. Phys. Fluids 2008, 20, 101505. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics: Non-Relativistic Theory; Pergamon Press, Ltd.: London, UK, 1958; pp. 133–144. [Google Scholar]
- Hellberg, C.S.; Orszag, S.A. Chaotic behavior of interacting elliptical instability modes. Phys. Fluids 1988, 31, 6–8. [Google Scholar] [CrossRef]
- Isaacson, L.K. Deterministic prediction of the entropy increase in a sudden expansion. Entropy 2011, 13, 402–421. [Google Scholar] [CrossRef]
- Press, W.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C: The Art of Scientific Computing, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992; pp. 710–714. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006; pp. 415–421. [Google Scholar]
- Rissanen, J. Complexity and information in data. In Entropy; Greven, A., Keller, G., Warnecke, G., Eds.; Princeton University Press: Princeton, NJ, USA, 2003; pp. 299–327. [Google Scholar]
- Rissanen, J. Information and Complexity in Statistical Modeling; Springer Science+Business Media, LLC: New York, NY, USA, 2007. [Google Scholar]
- Li, M.; Vitányi, P. An Introduction to Kolmogorov Complexity and Its Applications; Springer Science+Business Media, LLC: New York, NY, USA, 2008. [Google Scholar]
- Press, W.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C: The Art of Scientific Computing, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992; pp. 572–575. [Google Scholar]
- Grassberger, P.; Procaccia, I. Estimation of the Kolmogorov entropy from a chaotic signal. Phys. Rev. A 1983, 28, 2591–2593. [Google Scholar] [CrossRef]
- Cohen, A.; Procaccia, I. Computing the Kolmogorov entropy from time signals of dissipative and conservative dynamical systems. Phys. Rev. A 1985, 31, 1872–1882. [Google Scholar] [CrossRef] [PubMed]
- Pradeep, D.S.; Hussain, F. Core dynamics of a coherent structure: A protypical physical-space cascade mechanism? In Turbulence Structure and Vortex Dynamics; Hunt, J.C.R., Vassilicos, J.C.R., Eds.; Cambridge University Press: New York, NY, USA, 2011; pp. 54–82. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Isaacson, L.K. Control Parameters for Boundary-Layer Instabilities in Unsteady Shock Interactions. Entropy 2012, 14, 131-160. https://doi.org/10.3390/e14020131
Isaacson LK. Control Parameters for Boundary-Layer Instabilities in Unsteady Shock Interactions. Entropy. 2012; 14(2):131-160. https://doi.org/10.3390/e14020131
Chicago/Turabian StyleIsaacson, LaVar King. 2012. "Control Parameters for Boundary-Layer Instabilities in Unsteady Shock Interactions" Entropy 14, no. 2: 131-160. https://doi.org/10.3390/e14020131