Disentangling Complexity from Randomness and Chaos
Abstract
:1. Introduction
“Was sich überhaupt sagen läßt, läßt sich klar sagen; und wovon man nicht reden kann, darüber muß man schweigen.”(L. Wittgenstein, Tractatus Logico-Philosophicus)
“[A] variety of different measures would be required to capture all our intuitive ideas about what is meant by complexity and by its opposite, simplicity.”
“Perhaps the most dramatic [benefit] is that it yields a resolution to what has long been considered the single greatest mystery of the natural world: what secret is it that allows nature seemingly so effortlessly to produce so much that appears to us complex.”(p. 2)
2. Five Simple Models
2.1. The Kac Ring
2.2. Wolfram Cellular Automata
| Parent triplet | 1 1 1 | 1 1 0 | 1 0 1 | 1 0 0 | 0 1 1 | 0 1 0 | 0 0 1 | 0 0 0 |
|---|---|---|---|---|---|---|---|---|
| CA 30 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| CA 90 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| CA 110 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
2.3. The Bak-Sneppen Model
2.4. Model Results

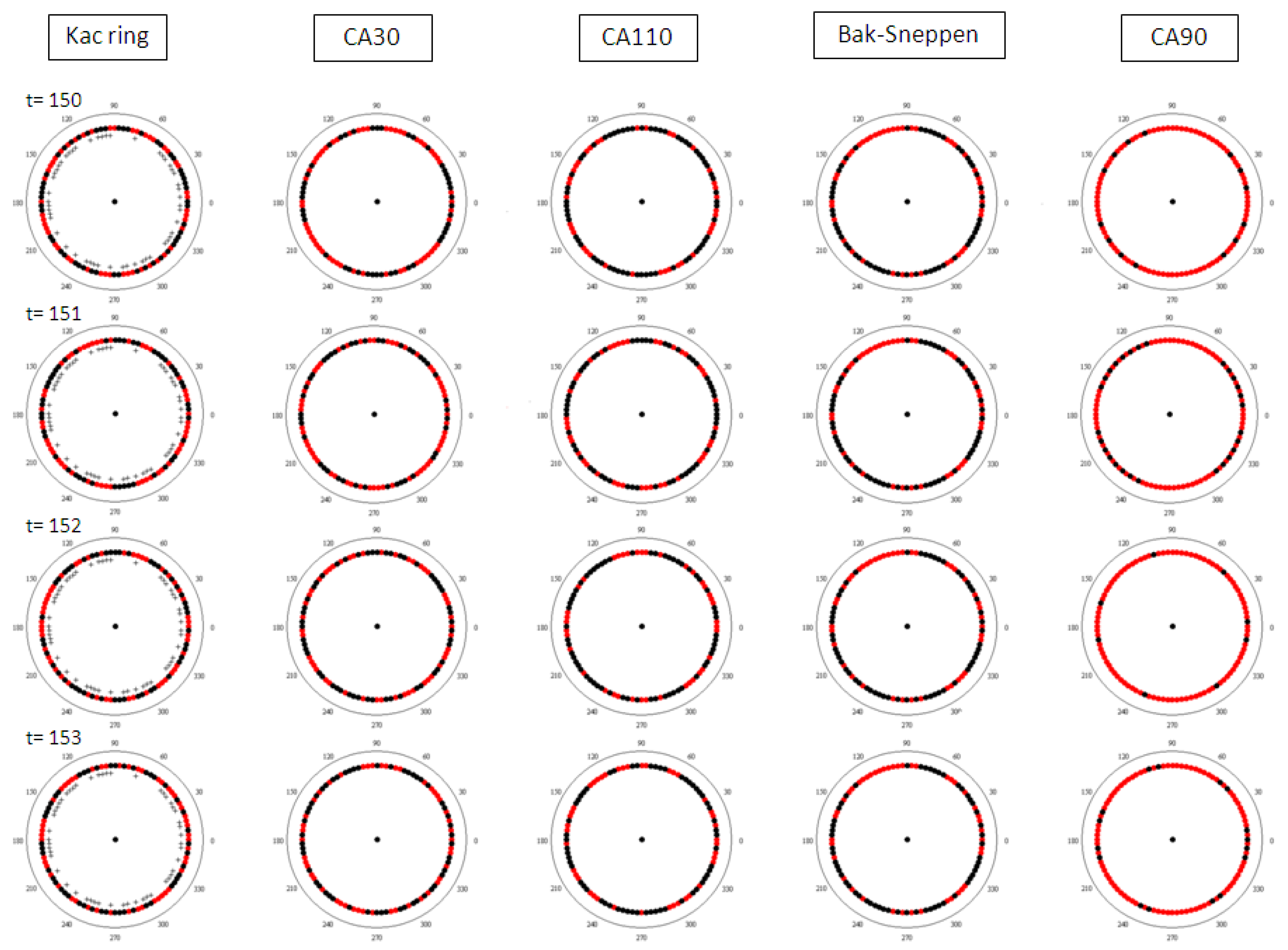
2.5. A Note on Boolean Networks
“The result was always the same. The model would converge either to the frozen phase or to the chaotic phase, and only if the parameter C [equivalent to k above] was tuned very carefully would we get interesting complex, critical behaviour. […] Despite Stu’s early enthusiastic claims, for instance in his book The Origins of Order, […] that they exhibit self-organized criticality, they simply don’t.”
| Parent triplet | 1 xn,t 1 | 1 xn,t 0 | 0 xn,t 1 | 0 xn,t 0 |
|---|---|---|---|---|
| AND | 1 | 0 | 0 | 0 |
| OR | 0 | 1 | 1 | 0 |
| TRUE | 1 | 1 | 1 | 1 |
| FALSE | 0 | 0 | 0 | 0 |
3. Dynamical Properties of Complex Systems
3.1. Complex Systems are Many-Component Systems
“From this illustration it is clear what is meant by a problem of disorganized complexity. It is a problem in which the number of variables is very large, and one in which each of the many variables has a behavior which is individually erratic, or perhaps totally unknown. However, in spite of this helter-skelter, or unknown, behavior of all the individual variables, the system as a whole possesses certain orderly and analyzable average properties.”(p. 539)
3.2. Complex Systems Feature Directed Interactions
3.3. Difference Between Complex and Chaotic Dynamics
“To be somewhat more technical, we could say that these complex systems have many degrees of freedom, and it is the activity of these many degrees of freedom that leads to the apparently random behaviour. […] The crucial importance of chaos is that it provides an alternative explanation for this apparent randomness—one that depends neither on noise nor on complexity. Chaotic behaviour shows up in systems that are essentially free from noise and are also relatively simple—only a few degrees of freedom are active.”(p. 8)
3.4. Benefits of a Dynamical Complexity Definition
4. Phenomenological Properties of Complex Systems
4.1. The Need for a Phenomenological Sieve
4.2. Where Does Complexity Manifest Itself?
“We are going to define a complex system as one with which we can interact effectively in many different kinds of ways, each requiring a different mode of system description.”(p. 29)
4.3. How Can Complexity be Described?
4.3.1. Semantic Circularity
“Class 1—evolution leads to a homogeneous state in which, for example, all sites have value 0.Class 2—evolution leads to a set of stable or periodic solutions that are separated and simple.Class 3—evolution leads to a chaotic pattern.Class 4—evolution leads to complex structures, sometimes long-lived.”(p. 9)
“[T]he intuitive notion is fairly clear: things seem complex if we don’t have a simple way to describe them.”(p. 131)
4.3.2. Metaphorical Over-Reach
4.3.2.1. Complexity Between Order and Disorder
“And finally [] class 4 involves a mixture of order and randomness: localised structures are produced which on their own are fairly simple, but these structures move around and interact with each other in very complicated ways.”(p. 235)

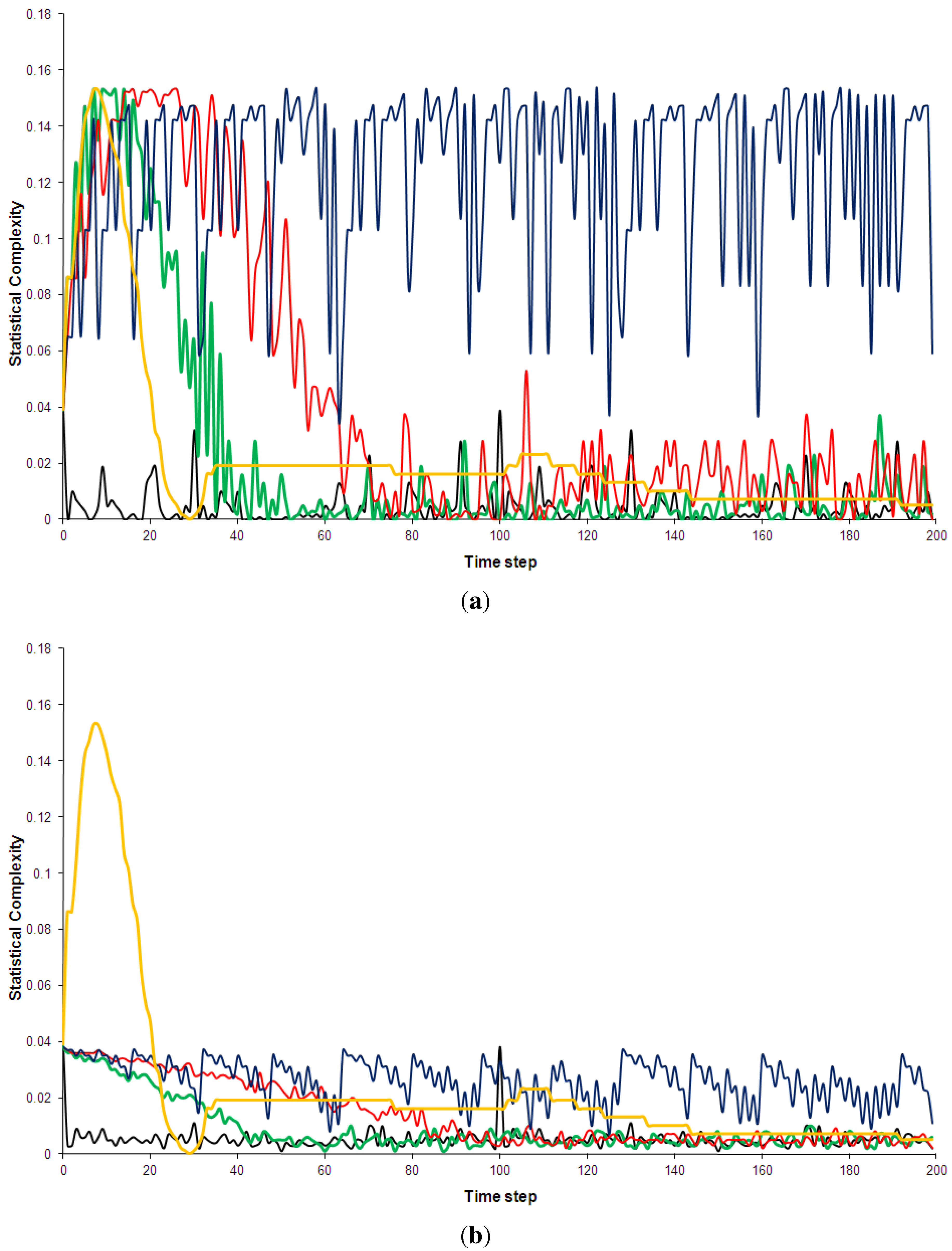
| Entropy | Complexity | |||
|---|---|---|---|---|
| Partition 1 | Partition 2 | Partition 1 | Partition 2 | |
| Kac ring | 0.985 | 0.980 | 0.00463 | 0.0053 |
| CA30 | 0.993 | 0.982 | 0.00475 | 0.00493 |
| CA110 | 0.980 | 0.982 | 0.0136 | 0.00505 |
| Bak-Sneppen | 0.984 | 0.972 | 0.0106 | 0.00762 |
| CA90 | 0.587 | 0.885 | 0.126 | 0.0240 |
“In general, their analysis has to be a meta-analysis, and in general it has to be based on meta-statistics instead of conventional first-order statistics.”(p. 828)
4.3.2.2. Complexity at the Edge of Chaos
“To the extent that one can make sense of what Packard and Langton meant by “the edge of chaos”, their interpretation of their simulation results are neither adequately supported nor are they correct on mathematical grounds.”(p. 276)
“But at the edge of chaos, the twinkling unfrozen islands are in tendrils of contact. Flipping any single lightbulb may send signals in small or large cascades of changes across the systems to distant sites, so the behaviours in time and across the webbed network might become coordinated. Yet since the system is at the edge of chaos, but not actually chaotic, the system will not veer into uncoordinated twitching”(p. 90)
4.3.2.3. Self-Organized Complexity
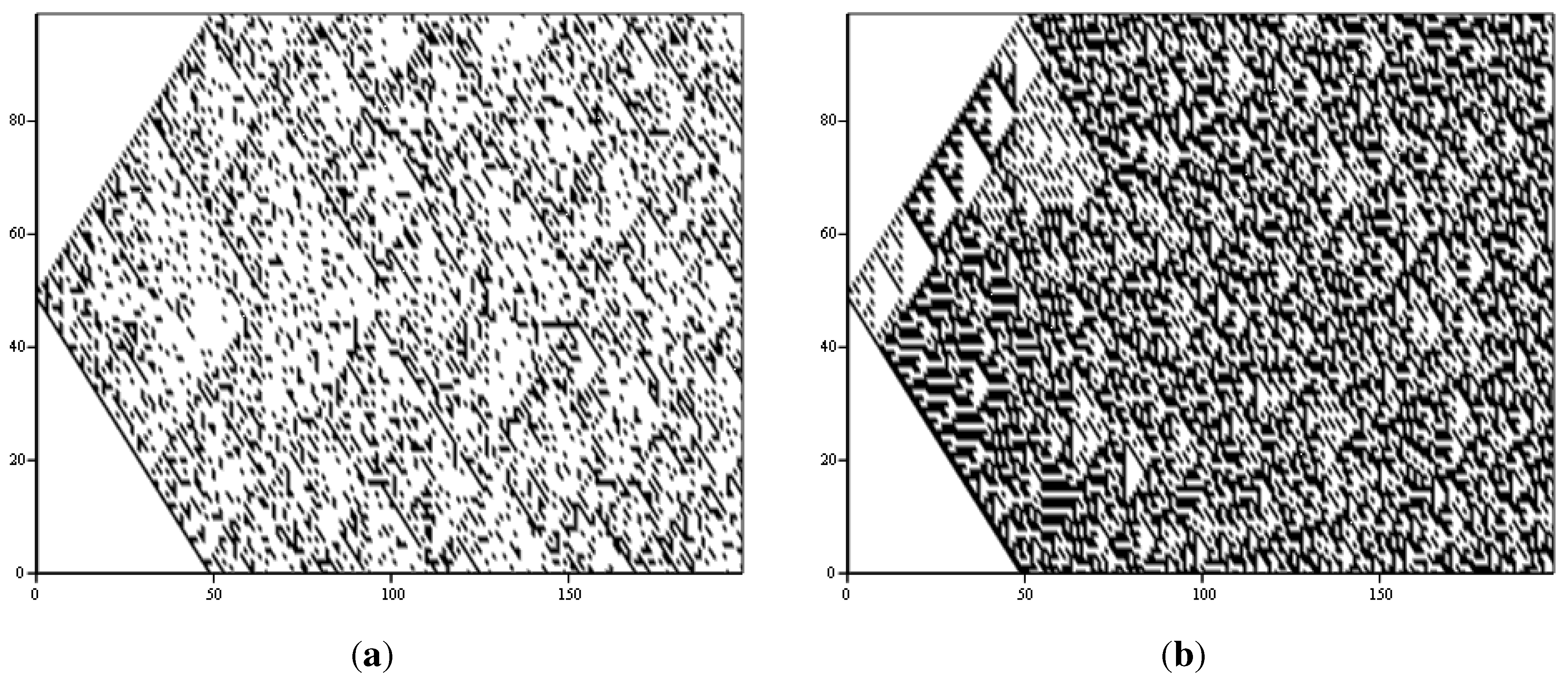
When viewed as mere descriptions of phenomenology, it seems doubtful whether the “self-organisation” metaphors add much to the descriptions of diagrams like the ones displayed in Figure 1 and Figure 2. For example, the expression “memory”, with its connotation of temporal continuity, could be employed to describe the elongated structure of dense, meso-scale triangles in the CA110 space-time diagram. However, this seems to improve little to the geometric description given in the second part of the last sentences—and introduces the faulty dynamical connotations exposed above.“Who or what else is organizing it [the brain] if it is not doing it itself? There are a number of ways that the brain can self-organize. What we want to know is which way it does it.”(p. 285)
5. Conclusions
Definition 1. A complex system is a many-component system with directed interactions for which locally distinct patterns can be recognized in at least one representation of its development.
“A complex system is an ensemble of many elements which are interacting in a disordered way, resulting in robust organisation and memory.”(p. 25)
Acknowledgements
References
- Gell-Mann, M. The Quark and the Jaguar: Adventures in the Simple and the Complex; W. H. Freemann: New York, NY, USA, 1994. [Google Scholar]
- Schaetzing, F. The Swarm; Regan Books: New York, NY, USA, 2006. [Google Scholar]
- Mitchell, M. Complexity: A Guided Tour; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Standish, R.K. Concept and Definition of Complexity. In Intelligent Complex Adaptive Systems; Yang, A., Shan, Y., Eds.; IGI Global: Hershey, PA, USA, 2008; pp. 105–124. [Google Scholar]
- Gell-Mann, M. What is complexity? Complexity 1995, 1, 1–9. [Google Scholar]
- Lloyd, S. Measures of complexity: A Nonexhaustive List. IEEE Control Syst. Mag. 2001, 21, 7–8. [Google Scholar] [CrossRef]
- Wolfram, S. A New Kind of Science; Wolfram Media: Champaign, IL, USA, 2002. [Google Scholar]
- Horgan, J. From complexity to perplexity. Sci. Am. 1995, 272, 104–110. [Google Scholar] [CrossRef]
- Meester, R.; Znamenski, D. Non-triviality of a discrete bak-sneppen evolution model. J. Stat. Phys. 2002, 109, 987–1004. [Google Scholar] [CrossRef]
- Coveney, P.; Highfield, R. Frontiers of Complexity: The Search for Order in a Chaotic World; Faber and Faber: London, UK, 1995. [Google Scholar]
- Kac, M. Some remarks on the use of probability on classical statistical mechanics. Bull. R. Belgium Acad. Sci. 1956, 53, 356–361. [Google Scholar]
- Dorfman, J.R. An Introduction to Chaos in Nonequilibrium Statistical Mechanics; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Gottwald, G.A.; Oliver, M. Boltzmann’s dilemma: An introduction to statistical mechanics via the kac ring. SIAM Rev. 2009, 51, 613–635. [Google Scholar] [CrossRef]
- von Neumann, J. Theory of Self-Reproducing Automata. In Theory of Self-Reproducing Automata; von Neumann, J., Burk, A.W., Eds.; University of Illinois Press: Urbana, IL, USA, 1966; pp. 29–296. [Google Scholar]
- Wolfram, S. Statistical mechanics of cellular automata. Rev. Mod. Phys. 1983, 55, 601–644. [Google Scholar] [CrossRef]
- Wolfram, S. Cellular automata. Los Alamos Science 1983, 9, 2–27. [Google Scholar]
- Wolfram, S. Universality and complexity in cellular automata. Physica D 1984, 10, 1–35. [Google Scholar] [CrossRef]
- Wolfram, S. Cellular automata as models of complexity. Nature 1984, 311, 419–424. [Google Scholar] [CrossRef]
- Wolfram, S. Twenty problems in the theory of cellular automata. Phys. Scr. 1985, 170. [Google Scholar] [CrossRef]
- Bak, P.; Sneppen, K. Punctuated equilibrium and criticality in a model of evolution. Phys. Rev. Lett. 1993, 71, 4083–4086. [Google Scholar] [CrossRef] [PubMed]
- Bak, P.; Paczuski, M. Complexity, contingency, and criticality. Proc. Natl. Acad. Sci. U. S. A. 1995, 92, 6689–6696. [Google Scholar] [CrossRef] [PubMed]
- Frigg, R. Self-organized criticality—What it is and what it isn’t. Stud. Hist. Philos. Sci. 2003, 34, 613–632. [Google Scholar] [CrossRef]
- Kauffmann, S. At Home In the Universe: The Search for Laws of Order and Complexity; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Kauffmann, S. The Origins of Order: Self-Organisation and Selection of Evolution; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Bak, P. How Nature Works: The Science of Self-Organized Criticality; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Waldrop, M.M. Complexity: The Emerging Science at the Edge of Order and Chaos; Penguin Books: London, UK, 1992. [Google Scholar]
- Brown, R. A brief account of microscopical observations made in the months of June, July and August, 1827, on the particles contained in the pollen of plants; and on the general existence of active molecules in organic and inorganic bodies. Philos. Mag. 1828, 4, 161–173. [Google Scholar]
- Weaver, W. Science and complexity. Am. Sci. 1948, 56, 536–547. [Google Scholar]
- Devaney, R.L. An Introduction To Chaotic Dynamical Systems; Addison Wesley: Redwood City, CA, USA, 1989. [Google Scholar]
- Hilborn, R.C. Chaos and Nonlinear Dynamics; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Werndl, C. What are the new implications of chaos for unpredictability? Br. J. Philos. Sci. 2009, 60, 195–220. [Google Scholar] [CrossRef]
- Chua, L.O.; Yoon, S.; Dogaru, R. A nonlinear dynamics perspective of wolfram’s new kind of science. Part I: Threshold of complexity. Int. J. Bifurc. Chaos 2002, 12, 2655–2766. [Google Scholar] [CrossRef]
- Werndl, C. Are deterministic and indeterministic descriptions observationally equivalent. Stud. Hist. Philos. Mod. Phys. 2009, 40, 232–242. [Google Scholar] [CrossRef] [Green Version]
- Davies, P. Introduction: Towards an Emergentist Worldview. In From Complexity to Life: On the Emergence of Life and Meaning; Gregersen, N.H., Ed.; Oxford University Press: Oxford, UK, 2003; pp. 3–19. [Google Scholar]
- Crutchfield, J.P.; Young, K. Inferring statistical complexity. Phys. Rev. Lett. 1989, 63, 105–108. [Google Scholar] [CrossRef] [PubMed]
- Crutchfield, J.P. The calculi of emergence: Computation, dynamics and induction. Physica D 1994, 74, 11–54. [Google Scholar] [CrossRef]
- Gregersen, N.H. From Complexity to Life: On the Emergence of Life and Meaning; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Gleick, J. Chaos: Making a New Science; Viking Penguin: New York, NY, USA, 1987. [Google Scholar]
- Solomonoff, R. A formal theory of inductive inference, Part 1 and Part 2. Inf. Control 1964, 7, 1–22, 224–254. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Three approaches to the quantitative definition of information. Probl. Inf. Transm. 1965, 1, 1–7. [Google Scholar] [CrossRef]
- Chaitin, G.J. On the length of programs for computing finite binary sequences. J. Assoc. Comput. Mach. 1966, 13, 547–569. [Google Scholar] [CrossRef]
- Chaitin, G.J. On the length of programs for computing finite binary sequences: Statistical considerations. J. Assoc. Comput. Mach. 1969, 16, 154–169. [Google Scholar] [CrossRef]
- Zurek, W.H. Algorithmic Information Content, Church-Turing Thesis, Physical Entropy and Maxwell’s Demon. In Complexity, Entropy and the Physics of Information; Zurek, W.H., Ed.; Addison-Wesley Longman: Redwood City, CA, USA, 1990; pp. 73–90. [Google Scholar]
- Turing, A.M. On computable numbers with an application to the entscheidungsproblem. Proc. Lond. Math. Soc. Ser. 2 1936, 42, 230–265. [Google Scholar]
- Nannen, V. A short introduction to kolmogorov complexity. Comput. Res. Repos. 2010, in press. [Google Scholar]
- Bennett, C.H. How to Define Complexity in Physics, and Why. In From Complexity to Life: On the Emergence of Life and Meaning; Gregersen, N.H., Ed.; Oxford University Press: Oxford, UK, 2003; pp. 34–47. [Google Scholar]
- Gell-Mann, M.; Lloyd, S. Effective Complexity. In Nonextensive Entropy: Interdisciplinary Applications; Gell-Mann, M., Tsallis, C., Eds.; Oxford University Press: Oxford, UK, 2004; pp. 387–398. [Google Scholar]
- Langton, C.G. Computation at the edge of chaos: Phase transitions and emergent computation. Physica D 1990, 42, 12–37. [Google Scholar] [CrossRef]
- Winsberg, E.P. Science in the Age of Computer Simulation; The University of Chicago Press: Chicago, IL, USA, 2010. [Google Scholar]
- Rosen, R. Complexity as a system property. Int. J. Gen. Syst. 1977, 3, 227–232. [Google Scholar] [CrossRef]
- Wolfram, S. Random sequence generation by cellular automata. Adv. Appl. Math. 1986, 7, 123–169. [Google Scholar] [CrossRef]
- Gershenson, C. Five Questions on Complexity; Automatic Press: Copenhagen, Denmark, 2008. [Google Scholar]
- Ladyman, J.; Lambert, J.; Wisener, K. What is a complex system? Preprint. 2011. Available online: http://www.philsci-archive.pitt.edu/8496/ (accessed on 1 February 2012).
- Edmonds, B. Syntactic Measures of Complexity. PhD thesis, University of Manchester, UK, 1999. [Google Scholar]
- Sethna, J.P. Statistical Mechanics: Entropy, Order Parameters, and Complexity; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Frigg, R.; Werndl, C. Entropy—A guide for the perplexed. preprint. 2011. Available online: http://www.philsci-archive.pitt.edu/8592/ (accessed on 1 February 2012).
- Feldman, D.P.; Crutchfield, J.P. Statistical measures of complexity, why? Phys. Lett. A 1998, 238, 244–252. [Google Scholar] [CrossRef]
- Lopez-Ruiz, R.; Mancini, H.L.; Calbet, X. A statistical measure of complexity. Phys. Lett. A 1995, 209, 321–326. [Google Scholar] [CrossRef]
- Martin, M.T.; Plastino, A.; Rosso, O.A. Statistical complexity and disequilibrium. Phys. Lett. A 2003, 311, 126–132. [Google Scholar] [CrossRef]
- Atmanspacher, H.; Raeth, C.; Wiedemann, G. Statistics and meta-statistics in the concept of complexity. Physica A 1997, 234, 819–826. [Google Scholar] [CrossRef]
- Packard, N.H.; Wolfram, S. Two dimensional cellular automata. J. Stat. Phys. 1985, 38, 901. [Google Scholar] [CrossRef]
- Mitchell, M.; P.Crutchfield, J.; Das, R. Evolving cellular automata with genetic algorithms: A review of recent work. In Proceedings of EvCa’96: Russian Academy of Science, Moscow, Russia, 1996; pp. 1–14 (pre-print).
- Strevens, M. Bigger than Chaos; Harvard University Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Bak, P.; Chen, K.; Creutz, M. Self-organized criticality in the ‘Game of Life’. Nature 1989, 342, 780–782. [Google Scholar] [CrossRef]
- Bawden, D. Organized complexity, meaning and understanding. New Inf. Perspect. 2007, 59, 307–327. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Beck, C. Generalized Information and Entropy Measures in Physics; Technical report. School of Mathematical Sciences, Queen Mary, University of London: London, UK, 2009. doi: http://arxiv.org/pdf/0902.1235v2.pdf.
- Boltzmann, L. Weitere Studien ueber das waermegleichgewicht unter gasmolekuelen. Wien. Ber. 1872, 66, 275–370. [Google Scholar]
- Boltzmann, L. Bemerkungen ueber einige Probleme der mechanischen Waermetheorie. Wien. Ber. 1877, 75, 62–100. [Google Scholar]
- Boltzmann, L. Ueber die Beziehung zwischen dem Hauptsatze der mechanischen Waermetheorie und der Wahrscheinlichkeitsrechnung respektive den Saetzen ueber das Waermegleichgewicht. Wien. Ber. 1877, 76, 373–435. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information Theory and Statistical Mechanics. II. Phys. Rev. 1957, 108, 171–190. [Google Scholar] [CrossRef]
- Shiner, P.T.; Davison, M.; Landsberg, P.T. Simple measure for complexity. Phys. Rev. E 1999, 59, 1459–1464. [Google Scholar] [CrossRef]
Appendices
A. Model Animations
- Kac.wmv
- CA30.wmv
- CA90.wmv
- CA110.wmv
- BakSneppen.wmv
B. Shannon Entropy
C. Statistical Complexity
C.1. Crutchfield’s Statistical Complexity
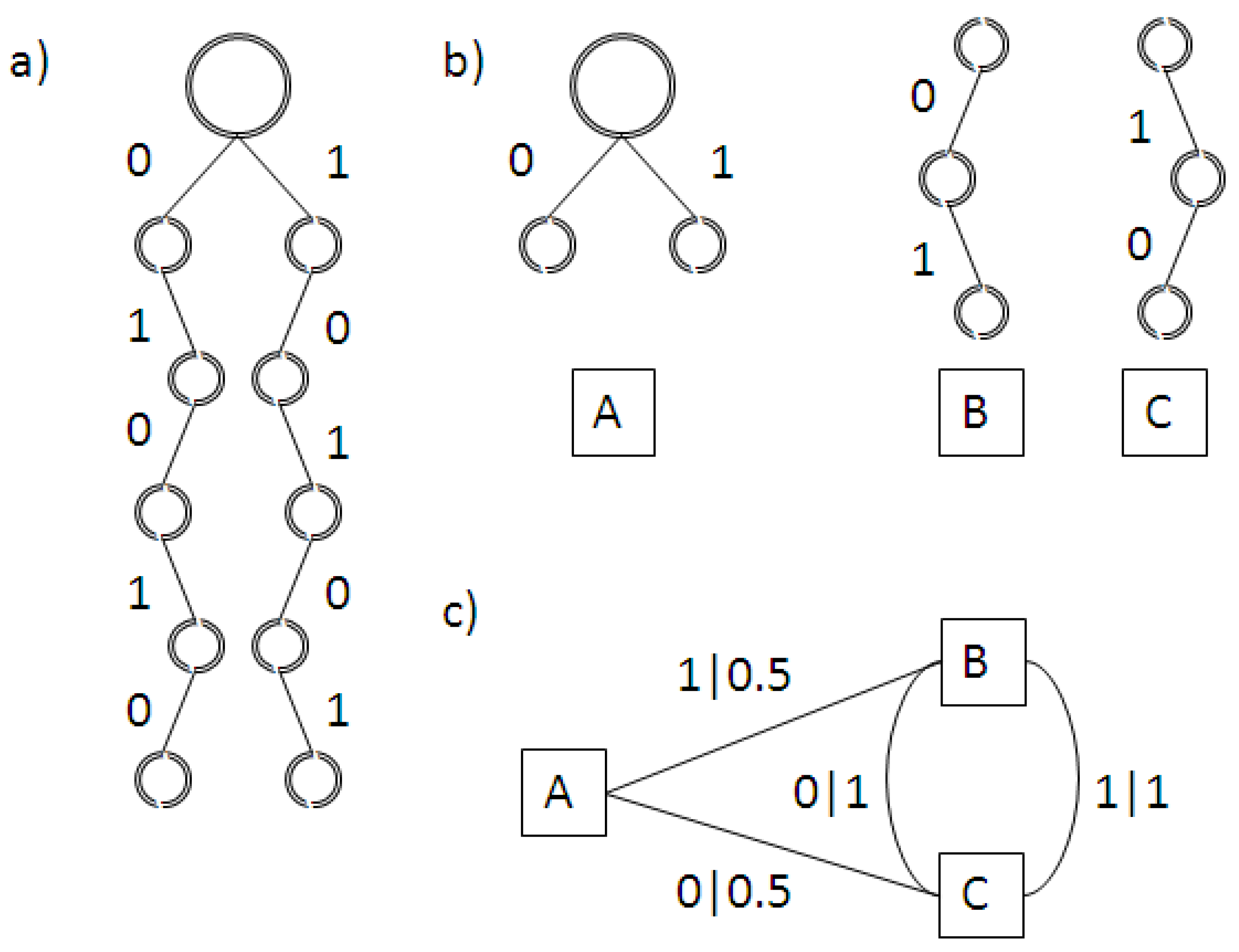
- The system is decoded into a string with an alphabet of N symbols . In most cases this means coarse graining the model’s phase space into N cells; e.g., for a system with the output of a simple sine curve a partition of P = could be assigned. If an element of the system is in the lower cell it will be represented by 0, if it is in the upper cell by 1. Depending on the length of the original time step, a periodic system will be encoded as a string similar to
- The decoded output string is then systematically parsed for patterns of a length L, which are collected in a parse tree. Figure C1a shows the L = 5 parse tree for the periodic string above.
- The parse tree is further decomposed into reoccurring sub-trees of length D called morphs (Figure C1b). Using the morphs, an ϵ- machine is constructed by decoding the full parse tree as an equivalent tree diagram for the morphs (Figure C1c). The ϵ-machine is called “minimal” if it uses the smallest possible number of morphs.
- Each edge e in the ϵ-machine is assigned a probability showing how likely the system is to proceed along this edge from one morph to another.
- The primary complexity measure from this algorithm is then estimated in analogy to the Shannon entropy in Equation (7):For our perfectly periodic example one thus obtains , as one might expect from a periodic system.
C.2. Simplified Statistical Complexity Measures
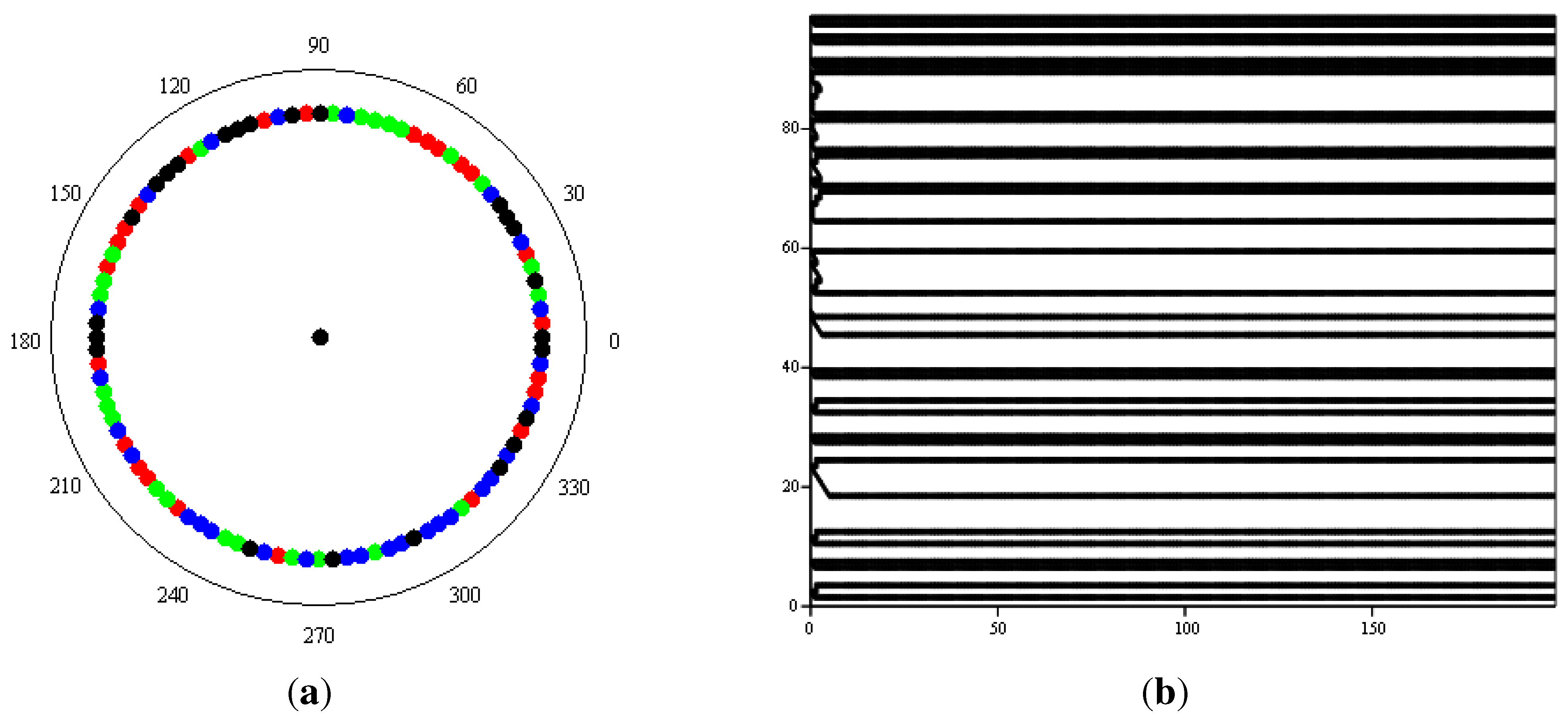
D. Phase Space Partitions
E. Random Runs

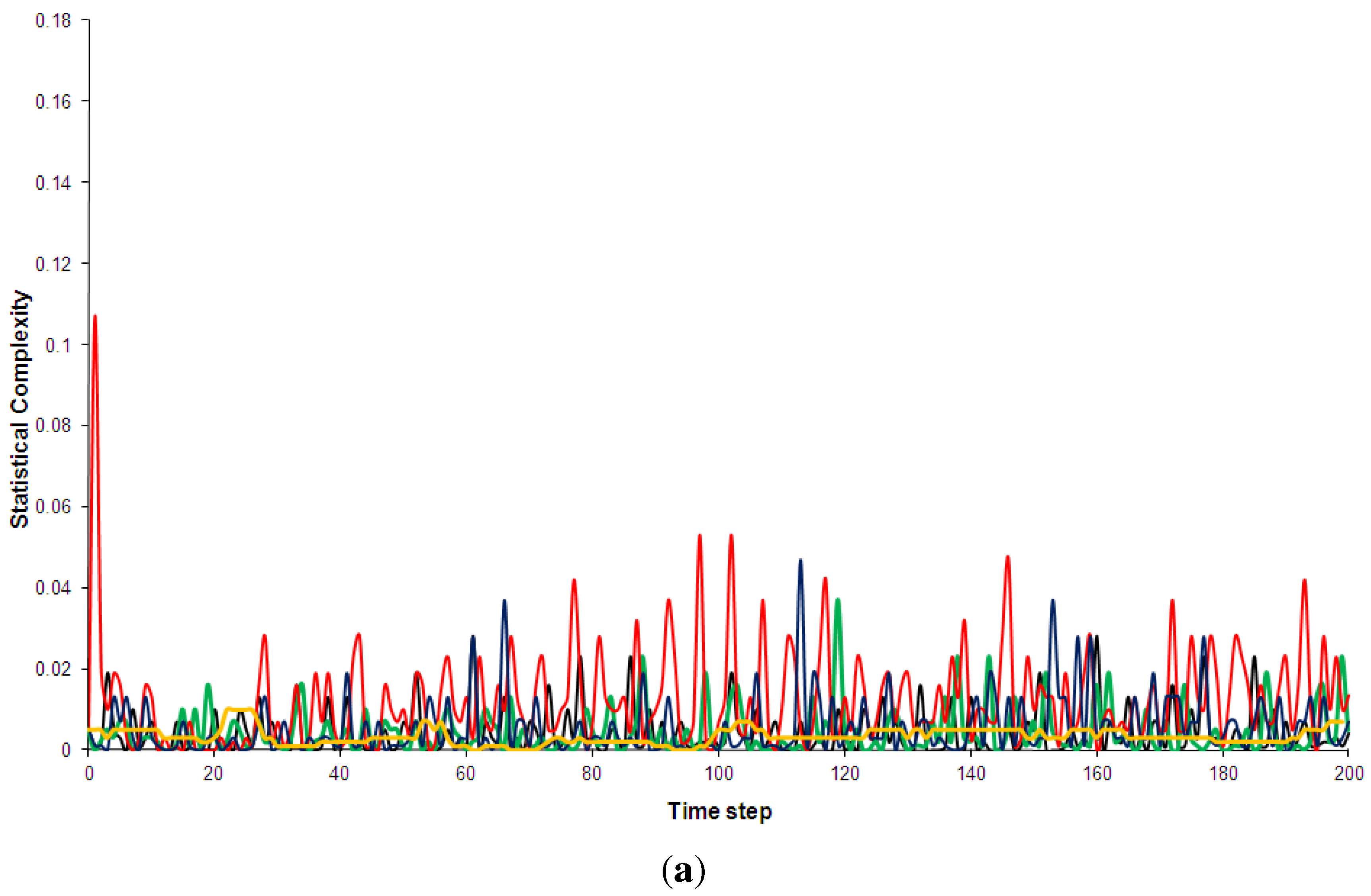

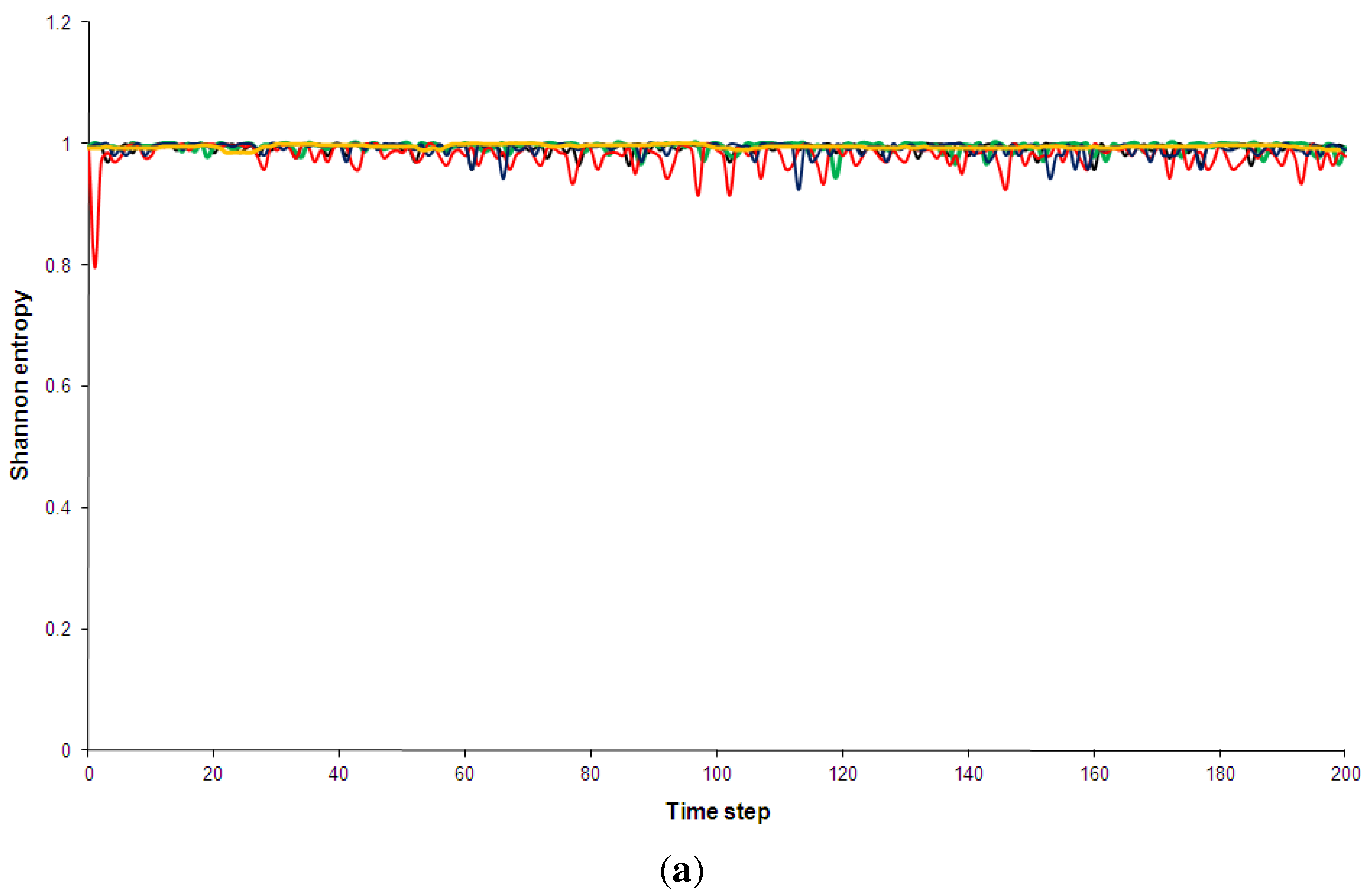
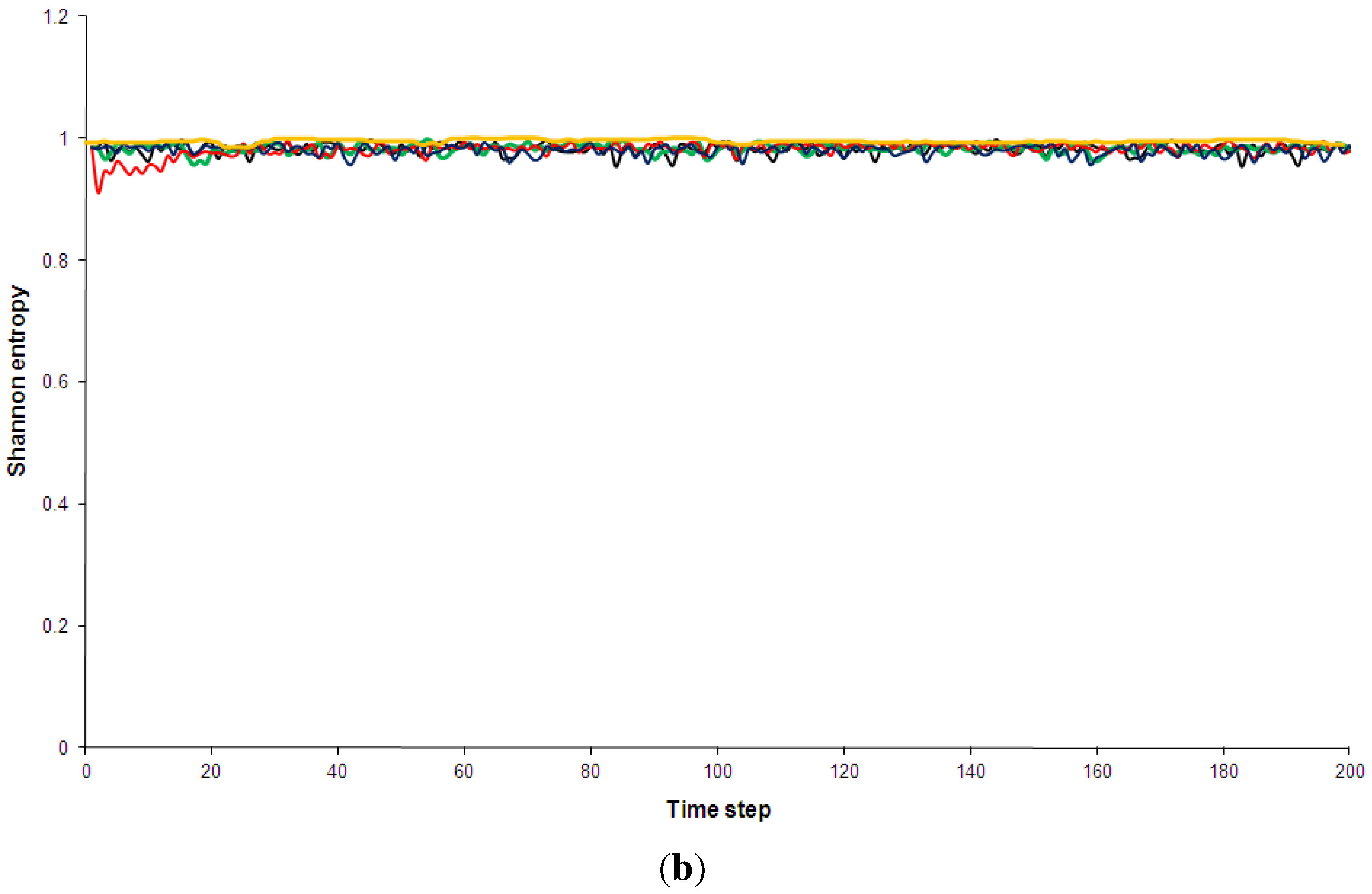
© 2012 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/.)
Share and Cite
Zuchowski, L.C. Disentangling Complexity from Randomness and Chaos. Entropy 2012, 14, 177-212. https://doi.org/10.3390/e14020177
Zuchowski LC. Disentangling Complexity from Randomness and Chaos. Entropy. 2012; 14(2):177-212. https://doi.org/10.3390/e14020177
Chicago/Turabian StyleZuchowski, Lena C. 2012. "Disentangling Complexity from Randomness and Chaos" Entropy 14, no. 2: 177-212. https://doi.org/10.3390/e14020177




