Computing the Topological Entropy of Multimodal Maps via Min-Max Sequences

Abstract

We derive an algorithm to recursively determine the lap number (minimal number of monotonicity segments) of the iterates of twice differentiable l-modal map, enabling to numerically calculate the topological entropy of these maps. The algorithm is obtained by the min-max sequences—symbolic sequences that encode qualitative information about all the local extrema of iterated maps.

1. Introduction

Entropy is a ubiquitous tool in physics and mathematics. It measures randomness in dynamical systems, uncertainty in information theory and disorder in statistical mechanics.

Topological entropy was introduced in 1965 by Adler, Konheim and McAndrew [1] as an invariant of topological conjugacy for maps of the interval. Along with the Lyapunov exponent, topological entropy is one of the preferred indicators for complexity in topological dynamics. The numerical computation of topological entropy has been and remains an active topic of research, as witnessed by a number of relevant publications in the last decades.

Let I be a compact interval $[a,b]\subset \mathbb{R}$ and $f:I\to I$ be a continuous piecewise monotone map. Such a map is called l-modal if f has precisely l turning points (i.e., points in $(a,b)$ where f has a local extremum). Assume that f has local extrema at $c_1<...<c_l$ and that f is strictly monotone in each of the $l+1$ intervals

$$I_1=[a,c_1),I_2=(c_1,c_2),...,I_{l+1}=(c_l,b]$$

To such map one can assign a positive or negative shape which describes whether f is increasing or decreasing on its first lap $I_1$. In proofs it is occasionally convenient to use the convention $c_0\equiv a$ and $c_{l+1}\equiv b$. Sometimes the additional condition $f\left(\right\{a,b\left\}\right)\subset \{a,b\}$ is also required (see for instance [2]); in this case we speak of boundary-anchored maps. We shall also consider boundary-anchored maps below but only as a special case, since the general algorithm for the topological entropy then simplifies quite a bit.

The itinerary of $x\in I$ under f is the sequence $\mathbf{i}\left(x\right)=(i_0\left(x\right),i_1\left(x\right),...,i_n\left(x\right),...)$ defined as follows:

$$i_n\left(x\right)=\left\{\begin{array}{cc}{I}_k& \text{if}{f}^n\left(x\right)\in I_k\hfill \\ c_k& \text{if}{f}^n\left(x\right)=c_k\hfill \end{array}\right.$$

The itineraries of the critical points,

$${\gamma }^i\equiv {\left({\gamma }_n^i\right)}_{n\in \mathbb{N}}=\mathbf{i}\left(c_i\right),1\le i\le l$$

are called the kneading sequences(or invariants) of f.

Let $h\left(f\right)$ denote the topological entropy of an l-modal map $f:I\to I$. Then [3,4],

$$\begin{array}{ccc}\hfill h\left(f\right)& =& \underset{n\to \infty }{lim}\frac{1}{n}{log}^{+}\text{Var}\left(f^n\right)\hfill \end{array}$$

(1)

$$\begin{array}{ccc}& =& \underset{n\to \infty }{lim}\frac{1}{n}log{\ell }_n\hfill \end{array}$$

(2)

where Var$\left(f^n\right)$ stands for the variation of $f^n$, and ${\ell }_n$ is shorthand for the lap number of $f^n$ (i.e., the number of maximal monotonicity segments of $f^n$). There are relations similar to (1) and (2), involving the number of fixed points of $f^n$ (i.e., the number of periodic points of period n), or the length of the graph of $f^n$.

The methods proposed in the literature to compute $h\left(f\right)$, use typically kneading sequences [5,6,7], approximating piecewise linear maps [8] and Markov maps [9], the Ruelle–Perron–Frobenius operator [10], or one of the expressions (1) and (2) [11,12]. Their virtues and shortcomings are also discussed in the literature. For instance, some are meant only for unimodal maps [5,7] or bimodal maps [6]. Others apply to not necessarily continuous piecewise monotone maps of the interval, however they are not efficient nor even accurate [8].

The method proposed here calculates the lap numbers ${\ell }_n$, $n\ge 1$, and the topological entropy follows from (2). It applies to multimodal maps with or without boundary conditions. The main ingredient of this approach are the so-called min-max sequences—symbolic sequences that encode the coarse-grained information about the extrema of the maps $f^n$, $n\ge 1$. It generalizes an approach for unimodal, boundary anchored maps, introduced in [13,14], further developed in [15], and extended for boundary free maps in [16].

The method proposed here is conceptually simple, is direct, is geometrical and is computationally efficient, calculating the lap numbers in a recursive way. The structure of the algorithm is the same for all l-modal maps, independently of the value of l. Regarding computing speed, we shall not provide any sharper bound than the $O(1/n)$ convergence rate derivable on general grounds [12]. Nonetheless, numerical simulations confirm the excellent performance of the algorithm—except when $h\left(f\right)\simeq 0$, in which case the convergence is slow.

The rest of the paper is organized as follows. In Section 2 we introduce the min-max sequences of a map $f\in {\mathcal{F}}_l$, where ${\mathcal{F}}_l$ is the class of twice differentiable l-modal maps. This assumption simplifies the proofs but the results obtained in this paper apply to the class of continuous piecewise monotonous maps. In Section 3, we derive a number of technical lemmas, which are needed in the next two sections. Section 4 is devoted to clarify the connection between the min-max sequences of a map and the structure of its extrema, exploring the geometrical meaning of the min-max sequences. This connection leads in Section 5 to the main result of the paper, Theorem 5.3, which provides a recursive scheme for computing ${\ell }_n$ (hence $h\left(f\right)$) with arbitrary precision. It turns out that the general scheme of Theorem 5.3 simplifies in some special cases, notably for boundary-anchored maps and for unimodal maps; these cases are separately discussed in Section 6. The paper concludes with the logical flow of the algorithm (Section 7), and a summary of numerical simulations with 2- and 3-modal maps (Section 8).

2. Geometry of the Itineraries: The Min-Max Sequences for l-Modal Maps

Henceforth we consider the class ${\mathcal{F}}_l$ of twice differentiable l-modal maps. Since the results we obtain in Section 5 for the calculation of lap numbers and topological entropy do not depend on the shape of f, we shall assume throughout that the shape of f is positive, that is,

$$f^{\prime }\left(x\right)>0\text{on}{I}_{\text{odd}},f^{\prime }\left(x\right)<0\text{on}{I}_{\text{even}}$$

(3)

where $I_{\text{odd}}$ [resp. $I_{\text{even}}$] denotes any $I_k$ with $k\in \{1,...,l+1\}$ odd [resp. even], and $f^{\prime }\left(a\right)$, $f^{\prime }\left(b\right)$ are meant to be the appropriate one-sided derivatives.

The chain rule for derivation applied to the nth iterate of f, written $f^n$ ($f^0$ is the identity map),

$$f^{n+1\prime }\left(x\right)={(f\circ f^n)}^{\prime }\left(x\right)=f^{\prime }\left(f^n\left(x\right)\right)f^{n\prime }\left(x\right)$$

(4)

implies trivially

$$f^n{}^{\prime }\left(x\right)=f^{\prime }\left(f^{n-1}\left(x\right)\right)f^{\prime }\left(f^{n-2}\left(x\right)\right)\cdots f^{\prime }\left(x\right)$$

(5)

which shows that $c_1,...,c_l$ are critical points of $f^n$ for every $n\ge 1$. From (5) we conclude also the following.

Lemma 2.1. 

If $f\in {\mathcal{F}}_l$, then the critical points of $f^n$, $n\ge 1$, are the points $x\in (a,b)$ such that $f^k\left(x\right)=c_i$ for some $0\le k\le n-1$ and $1\le i\le l$.

Therefore, the critical points of $f^n$ with $n\ge 1$ are the pre-images of the critical points $c_1$,..., $c_l$ up to order $n-1$.

Our next scope is a relation between the kneading sequences of $f\in {\mathcal{F}}_l$ and the structure of local extrema of $f^n$. According to the assumption (3),

$$f\left(c_i\right)\text{is}\text{a}\left\{\begin{array}{c}\hfill \text{ maximum if }i\text{ is odd}\\ \hfill \text{ minimum if }i\text{ is even}\end{array}\right.$$

(6)

where $1\le i\le l$.

The next lemma follows readily from (4) and

$$f^{n+1\prime \prime }\left(x\right)=f^{\prime \prime }\left(f^n\left(x\right)\right){\left(f^{n\prime }\left(x\right)\right)}^2+f^{\prime }\left(f^n\left(x\right)\right)f^{n\prime \prime }\left(x\right)$$

(7)

Lemma 2.2. 

Let $f\in {\mathcal{F}}_l$, and $n\ge 1$. Then:

(a) 

If $f^n\left(x\right)=c_i$ with i odd, then $f^{n+1}\left(x\right)$ is a maximum. If $f^n\left(x\right)=c_i$ with i even, then $f^{n+1}\left(x\right)$ is a minimum.

(b) 

If $f^n\left(x\right)$ is a minimum, then

$$f^{n+1}\left(x\right)isa\left\{\begin{array}{cc}minimum& if{f}^n\left(x\right)\in I_{odd}\hfill \\ maximum& if{f}^n\left(x\right)\in I_{even}\hfill \end{array}\right.$$

(b) 

If $f^n\left(x\right)$ is a maximum, then

$$f^{n+1}\left(x\right)\text{is}\text{a}\left\{\begin{array}{cc}maximum& if{f}^n\left(x\right)\in I_{odd}\hfill \\ minimum& if{f}^n\left(x\right)\in I_{even}\hfill \end{array}\right.$$

For our purposes it will be sufficient to know which element of the partition $\mathcal{P}=\{I_1,c_1,I_{2,}...,c_l,I_{l+1}\}$ the points $f^n\left(a\right)$, $f^n\left(c_i\right)$ and $f^n\left(b\right)$ belong to. This information can be conveniently codified by assigning to $x\in [a,b]$ a signature $\sigma \left(x\right)\equiv \sigma =({\sigma }_1,{\sigma }_2,...,{\sigma }_l)\in {\{-,0,+\}}^l$ defined as follows: For $i=1,...,l$,

$${\sigma }_i\left(x\right)=\left\{\begin{array}{cc}\hfill -& \text{if }x<c_i\\ \hfill 0& \text{if }x=c_i\\ \hfill +& \text{if }x>c_i\end{array}\right.$$

(8)

Therefore there are only $2l+1$ signatures, one for each element of $\mathcal{P}$. Note that if $x\in I_{i_0}$, $i_0\ge 2$, then

$${\sigma }_1,...,{\sigma }_{i_0-1}=+\text{,}\text{and}{\sigma }_{i_0},...,{\sigma }_l=-$$

(9)

Otherwise, if $x=c_{j_0}$, $1<j_0<l$, then

$${\sigma }_1,...,{\sigma }_{j_0-1}=+\text{,}{\sigma }_{j_0}=0\text{,}\text{and}{\sigma }_{j_0+1},...,{\sigma }_l=-$$

(10)

The cases $i_0=1$, $j_0=1$ or $j_0=l$ need no further comments. Thus, in a signature the +’s appear always left of the −’s, occasionally separated by a 0.

Two further tools will prove useful later on.

• We borrow from the real analysis a product ‘·’ among the symbols ${\sigma }_i\in \{-,0,+\}$:

  $$-·-=+·+=+,-·+=+·-=-,-·0=0·0=0·+=0$$
• If $x<y$ in $[a,b]$, then $\sigma \left(x\right)\le \sigma \left(y\right)$, where here < stands for the lexicographical order of signatures induced by $-<0<+$.

Suppose that $f^n$, $n\ge 1$, has a maximum [resp. minimum] at some point $x\in I=[a,b]$. We say that $f^n\left(x\right)$ is a maximum [resp. minimum] with signature $\sigma =({\sigma }_1,{\sigma }_2,...,{\sigma }_l)$ if $\sigma =\sigma \left(f^n\left(x\right)\right)$. Sometimes we also say that $f^n\left(x\right)$ is a σ-maximum [resp. σ-minimum] with the obvious meaning.

To locate the extrema of $f^n$ in I up to the precision set by the partition $\mathcal{P}$, we introduce a new alphabet

$$\mathcal{M}=\{m^{\sigma },M^{\sigma }\}$$

(11)

where m stands for “minimum”, M stands for “maximum”, and the superscript σ is the pertaining signature, i.e., if $f^n\left(x\right)$ is the minimum or maximum considered, then $\sigma =\sigma \left(f^n\left(x\right)\right)$. Correspondingly we say that $f^n\left(x\right)$ is an extremum of type $m^{\sigma }$ [resp. $M^{\sigma }$], or just that $f^n\left(x\right)$ is a σ-minimum [resp. σ-maximum].

Next we define l sequences ${\omega }^i={\left({\omega }_n^i\right)}_{n\ge 1}\in {\mathcal{M}}^{\mathbb{N}}$, $1\le i\le l$, as follows:

$${\omega }_n^i=\left\{\begin{array}{cc}{m}^{\sigma }\hfill & \text{if}{f}^n\left(c_i\right)\text{is}\text{a}\text{minimum}\text{of}\text{type}\sigma \hfill \\ M^{\sigma }\hfill & \text{if}{f}^n\left(c_i\right)\text{is}\text{a}\text{maximum}\text{of}\text{type}\sigma \hfill \end{array}\right.$$

The sequences ${\omega }^1,...,{\omega }^l$ are called the min-max sequences of $f\in {\mathcal{F}}_l$, or MMSs for short. The geometric meaning of ${\omega }_n^i$ is clear: $f^n\left(c_i\right)$ is a maximum (if ${\omega }_n^i=M^{\sigma }$) or a minimum (if ${\omega }_n^i=m^{\sigma }$) with signature $\sigma \equiv \sigma \left({\omega }_n^i\right)$.

By particularizing Lemma 2.2 to $x=c_{2k+1}$, $0\le k\le ⌊(l-1)/2⌋$, and $x=c_{2k}$, $1\le k\le ⌊l/2⌋$, we get the transition rules listed in Table 1.

Table 1. Consecutive symbols in the MMS follow the above transition rules.

${\omega }_n^i$	→	${\omega }_{n+1}^i$
$m^{(+,...,+,{\sigma }_{2k+1}=0,-,...,-)},M^{(+,...,+,{\sigma }_{2k+1}=0,-,...,-)}$	→	$M^{\sigma \left({\gamma }_{n+1}^i\right)}$
$m^{(+,...,+,{\sigma }_{2k}=0,-,...,-)},M^{(+,...,+,{\sigma }_{2k}=0,-,...,-)}$	→	$m^{\sigma \left({\gamma }_{n+1}^i\right)}$
$m^{(+,...,+,{\sigma }_{2k+1}=-,...,-)}$	→	$m^{\sigma \left({\gamma }_{n+1}^i\right)}$
$m^{(+,...,+,{\sigma }_{2k}=-,...,-)}$	→	$M^{\sigma \left({\gamma }_{n+1}^i\right)}$
$M^{(+,...,+,{\sigma }_{2k+1}=-,...,-)}$	→	$M^{\sigma \left({\gamma }_{n+1}^i\right)}$
$M^{(+,...,+,{\sigma }_{2k}=-,...,-)}$	→	$m^{\sigma \left({\gamma }_{n+1}^i\right)}$

Table 1. Consecutive symbols in the MMS follow the above transition rules.

${\omega }_n^i$	→	${\omega }_{n+1}^i$
$m^{(+,...,+,{\sigma }_{2k+1}=0,-,...,-)},M^{(+,...,+,{\sigma }_{2k+1}=0,-,...,-)}$	→	$M^{\sigma \left({\gamma }_{n+1}^i\right)}$
$m^{(+,...,+,{\sigma }_{2k}=0,-,...,-)},M^{(+,...,+,{\sigma }_{2k}=0,-,...,-)}$	→	$m^{\sigma \left({\gamma }_{n+1}^i\right)}$
$m^{(+,...,+,{\sigma }_{2k+1}=-,...,-)}$	→	$m^{\sigma \left({\gamma }_{n+1}^i\right)}$
$m^{(+,...,+,{\sigma }_{2k}=-,...,-)}$	→	$M^{\sigma \left({\gamma }_{n+1}^i\right)}$
$M^{(+,...,+,{\sigma }_{2k+1}=-,...,-)}$	→	$M^{\sigma \left({\gamma }_{n+1}^i\right)}$
$M^{(+,...,+,{\sigma }_{2k}=-,...,-)}$	→	$m^{\sigma \left({\gamma }_{n+1}^i\right)}$

The signature $\sigma \left({\gamma }_{n+1}^i\right)$ appearing on the right column is given as in (8) with $x=c_i$. Thus, once we know the kneading sequences ${\gamma }^i$, $1\le i\le l$, and the initial components of the MMSs, ${\omega }_1^i$, we can calculate the MMSs ${\omega }^i$ of f by means of the transition rules in Table 1.

3. Auxiliary Lemmas

As stated before, the generic structure of a signature is

$$(+,...,+,-,...,-)\text{or}(+,...,+,0,-,...,-)$$

Therefore, when comparing component-wise two signatures, only three cases can happen: (i) all components coincide, (ii) they differ in a single component, or (iii) they differ in a number of consecutive components. Of course, case (ii) can be considered as a “degenerate” subcase of (iii), as we will do in the sequel.

Let $f\in {\mathcal{F}}_l$ and set,

$${\mathcal{S}}^n=\{x\in I:f^n{}^{\prime }\left(x\right)=0\}$$

(12)

In particular, ${\mathcal{S}}^1=\{c_1,...,c_l\}$. According to Lemma 2.1, ${\mathcal{S}}^n$ contains ${\mathcal{S}}^1$ and its preimages up to order $n-1$. This same lemma implies that if $x\in (a,b)$ is a critical point of $f^n$, $n\ge 1$, then x is also a critical point of $f^k$ for $k>n$. Hence, ${\mathcal{S}}^n\subset {\mathcal{S}}^{n+1}$. It follows from Lemma 2.2 that all these critical points are local maxima or minima, but not inflexion points.

Furthermore, let ${\xi }_n$ [resp. ${\eta }_n$] be the leftmost [resp. rightmost] critical point of $f^n$, i.e.,

$${\xi }_n=min{\mathcal{S}}^n,{\eta }_n=max{\mathcal{S}}^n$$

(13)

for $n\ge 1$. Observe that ${\xi }_1=c_1$ and ${\eta }_1=c_l$.

Lemma 3.1. 

Let $f\in {\mathcal{F}}_l$ and $z_{n,1}<z_{n,2}$, $n\ge 1$, be

• two consecutive critical points of $f^n$ ($n\ge 2$ if $l=1$), or
• $z_{n,1}=a$ and $z_{n,2}={\xi }_n$, or
• $z_{n,1}={\eta }_n$, and $z_{n,2}=b$.

Then,

(a) 

If ${\sigma }_i\left(f^n\left(z_{n,1}\right)\right)·{\sigma }_i\left(f^n\left(z_{n,2}\right)\right)<0$ for $i_0\le i\le i_0+j_0-1$ ($i_0\in \{1,...,l\}$, $j_0\in \{1,...,l-i_0+1\}$) and ${\sigma }_i\left(f^n\left(z_{n,1}\right)\right)·{\sigma }_i\left(f^n\left(z_{n,2}\right)\right)\ge 0$ otherwise, then there exist $j_0$ critical points $z_{n+1,1}$,..., $z_{n+1,j_0}$ of $f^{n+1}$ in $(z_{n,1},z_{n,2})$. Furthermore, $f^n\left(z_{n+1,j}\right)=c_{i_0+j-1}$, $1\le j\le j_0$, and $f^{n+1}$ has a maximum at $z_{n+1,j}$ if $i_0+j$ is even (hence $f^{n+1}\left(z_{n+1,j}\right)$ is a $\sigma \left(f\left(c_{i_0+j-1}\right)\right)$-maximum in this case), while $f^{n+1}$ has a minimum at $z_{n+1,j}$ if $i_0+j$ is odd (hence $f^{n+1}\left(z_{n+1,j}\right)$ is a $\sigma \left(f\left(c_{i_0+j-1}\right)\right)$-minimum in this case). Moreover, $z_{n+1,1}<...<z_{n+1,j_0}$ if $f^n\left(z_{n,1}\right)<f^n\left(z_{n,2}\right)$, while $z_{n+1,1}>...>z_{n+1,j_0}$ if $f^n\left(z_{n,1}\right)>f^n\left(z_{n,2}\right)$.

(b) 

Otherwise (i.e., ${\sigma }_i\left(f^n\left(z_{n,1}\right)\right)·{\sigma }_i\left(f^n\left(z_{n,2}\right)\right)\ge 0$ for $1\le i\le l$), there exist no critical points of $f^{n+1}$ in $(z_{n,1},z_{n,2})$.

The geometrical interpretation of this lemma in the Cartesian plane $(x,y)$ is clear. If $j_0=1$ in (a), then the curve $y=f^n\left(x\right)$, $z_{n,1}\le x\le z_{n,2}$, crosses transversally the “ith critical line” $y=c_i$ , and none of the other critical lines (if any) $y=c_k$, $k\ne i$. If $j_0>1$, then this curve crosses transversally $j_0$ successive critical lines, namely, $y=c_{i_0}$ up to $y=c_{i_0+j_0-1}$, and none of the remaining ones (if any). In (b) both $f^n\left(z_{n,1}\right))$ and $f^n\left(z_{n,2}\right))$ belong to the same interval $I_i\in \mathcal{P}$, so $y=f^n\left(x\right)$ does not cross any critical line when $x\in (z_{n,1},z_{n,2})$.

Proof. 

(a) Suppose $c_{i_0-1}<f^n\left(z_{n,1}\right)<c_{i_0}<...<c_{i_0+j_0-1}<f^n\left(z_{n,2}\right)<c_{i_0+j_0}$ (the case $c_{i_0-1}<f^n\left(z_{n,2}\right)<c_{i_0}<...<c_{i_0+j_0-1}<f^n\left(z_{n,1}\right)<c_{i_0+j_0}$ follows analogously). By the monotonicity of $f^n$ in $[z_{n,1},z_{n,2}]$ and the Mean Value Theorem, there exist exactly $j_0$ different points $z_{n+1,1},...,z_{n+1,j_0}\in (z_{n,1},z_{n,2})$ such that $f^n\left(z_{n+1,j}\right)=c_{i_0+j-1}$ for $1\le j\le j_0$. Then

$$f^{n+1\prime }\left(z_{n+1,j}\right)=f^{\prime }\left(c_{i_0+j-1}\right)f^{n\prime }\left(z_{n+1,j}\right)=0$$

and

$$f^{n+1\prime \prime }\left(z_{n+1,j}\right)=f^{\prime \prime }\left(c_{i_0+j-1}\right){\left(f^{n\prime }\left(z_{n+1,j}\right)\right)}^2$$

Therefore,

$$f^{n+1\prime \prime }\left(z_{n+1,j}\right)\left\{\begin{array}{cc}<0& \text{if}{i}_0+j-1\text{is}\text{odd}\\ >0& \text{if}{i}_0+j-1\text{is}\text{even}\end{array}\right.$$

because according to (6), $f\left(c_{i_0+j-1}\right)$ is a maximum in the first case, and a minimum in the second.

The statement about the relative positions of $z_{n+1,j}$, $1\le j\le j_0$ is obvious from the geometrical interpretation.

(b) This assertion is straightforward. ☐

Setting $z_{n,1}=a$, $z_{n,2}={\xi }_n$ in Lemma 3.1, we conclude the following results.

Lemma 3.2. 

Let $f\in {\mathcal{F}}_l$ and $n\ge 1$.

(a) 

If ${\sigma }_i\left(f^n\left(a\right)\right)·{\sigma }_i\left(f^n\left({\xi }_n\right)\right)<0$ for $i_0\le i\le i_0+j_0-1$ ($i_0\in \{1,...,l\}$, $j_0\in \{1,...,l-i_0+1\}$) and ${\sigma }_i\left(f^n\left(a\right)\right)·{\sigma }_i\left(f^n\left({\xi }_n\right)\right)\ge 0$ otherwise, then ${\xi }_{n+1}<{\xi }_n$. Furthermore, if $f^n\left(a\right)<f^n\left({\xi }_n\right)$, then $f^n\left({\xi }_{n+1}\right)=c_{i_0}$, and $f^{n+1}\left({\xi }_{n+1}\right)$ is a $\sigma \left(f\left(c_{i_0}\right)\right)$-maximum if $i_0$ is odd or a $\sigma \left(f\left(c_{i_0}\right)\right)$-minimum if $i_0$ is even. If $f^n\left(a\right)>f^n\left({\xi }_n\right)$, then $f^n\left({\xi }_{n+1}\right)=c_{i_0+j_0-1}$, and $f^{n+1}\left({\xi }_{n+1}\right)$ is a $\sigma \left(f\left(c_{i_0+j_0-1}\right)\right)$-maximum if $i_0+j_0$ is even or a $\sigma \left(f\left(c_{i_0+j_0-1}\right)\right)$-minimum if $i_0+j_0$ is odd.

(b) 

Otherwise (i.e., ${\sigma }_i\left(f^n\left(a\right)\right)·{\sigma }_i\left(f^n\left({\xi }_n\right)\right)\ge 0$ for $1\le i\le l$), ${\xi }_{n+1}={\xi }_n$ holds. Furthermore,

(b1) 

$f^{n+1}\left({\xi }_{n+1}\right)$ is a maximum if (i) $f^n\left({\xi }_n\right)$ is a maximum and $f^n\left({\xi }_n\right)\in I_{odd}$, or (ii) $f^n\left({\xi }_n\right)$ is a minimum and $f^n\left({\xi }_n\right)\in I_{even}$;

(b2) 

$f^{n+1}\left({\xi }_{n+1}\right)$ is a minimum if (i) $f^n\left({\xi }_n\right)$ is a maximum and $f^n\left({\xi }_n\right)\in I_{even}$, or (ii) $f^n\left({\xi }_n\right)$ is a minimum and $f^n\left({\xi }_n\right)\in I_{odd}$.

Proof. 

(a) is a corollary of Lemma 3.1 (a). The first statement of (b) is a corollary of Lemma 3.1 (b).

As for (b1) and (b2),

$$f^{n+1\prime }\left({\xi }_{n+1}\right)=f^{\prime }\left(f^n\left({\xi }_n\right)\right)f^{n\prime }\left({\xi }_n\right)=0$$

because ${\xi }_n$ is a critical point of $f^n$. Moreover,

$$f^{n+1\prime \prime }\left({\xi }_{n+1}\right)=f^{\prime }\left(f^n\left({\xi }_n\right)\right)f^{n\prime \prime }\left({\xi }_n\right)$$

Thus, $f^{n+1\prime \prime }\left({\xi }_{n+1}\right)$ and $f^{n\prime \prime }\left({\xi }_n\right)$ have the same sign if and only if $f^n\left({\xi }_n\right)\in I_{\text{odd}}$ (so as $f^{\prime }\left(f^n\left({\xi }_n\right)\right)>0$, see (3)). ☐

And setting $z_{n,1}={\eta }_n$, $z_{n,2}=b$ in Lemma 3.1, we derive the following results in a way similar to Lemma 3.2.

Lemma 3.3. 

Let $f\in {\mathcal{F}}_l$ and $n\ge 1$.

(a) 

If ${\sigma }_i\left(f^n\left({\eta }_n\right)\right)·{\sigma }_i\left(f^n\left(b\right)\right)<0$ for $i_0\le i\le i_0+j_0-1$ ($i_0\in \{1,...,l-1\}$, $j_0\in \{2,...,l-i_0+1\}$) and ${\sigma }_i\left(f^n\left({\eta }_n\right)\right)·{\sigma }_i\left(f^n\left(b\right)\right)\ge 0$ otherwise, then ${\eta }_{n+1}>{\eta }_n$. Furthermore, if $f^n\left({\eta }_n\right)<f^n\left(b\right)$, then $f^n\left({\eta }_{n+1}\right)=c_{i_0+j_0-1}$, and $f^{n+1}\left({\eta }_{n+1}\right)$ is a $\sigma \left(f\left(c_{i_0+j_0-1}\right)\right)$-maximum if $i_0+j_0$ is even or a $\sigma \left(f\left(c_{i_0+j_0-1}\right)\right)$-minimum if $i_0+j_0$ is odd. If $f^n\left({\eta }_n\right)>f^n\left(b\right)$, then $f^n\left({\eta }_{n+1}\right)=c_{i_0}$, and $f^{n+1}\left({\eta }_{n+1}\right)$ is a $\sigma \left(f\left(c_{i_0}\right)\right)$-maximum if $i_0$ is odd or a $\sigma \left(f\left(c_{i_0}\right)\right)$-minimum if $i_0$ is even.

(b) 

Otherwise (i.e., ${\sigma }_i\left(f^n\left({\eta }_n\right)\right)·{\sigma }_i\left(f^n\left(b\right)\right)\ge 0$ for $1\le i\le l$), ${\eta }_{n+1}={\eta }_n$ holds. Furthermore,

(b1) 

$f^{n+1}\left({\eta }_{n+1}\right)$ is a maximum if (i) $f^n\left({\eta }_n\right)$ is a maximum and $f^n\left({\eta }_n\right)\in I_{odd}$, or (ii) $f^n\left({\eta }_n\right)$ is a minimum and $f^n\left({\eta }_n\right)\in I_{even}$;

(b2) 

$f^{n+1}\left({\eta }_{n+1}\right)$ is a minimum if (i) $f^n\left({\eta }_n\right)$ is a maximum and $f^n\left({\eta }_n\right)\in I_{even}$, or (ii) $f^n\left({\eta }_n\right)$ is a minimum and $f^n\left({\eta }_n\right)\in I_{odd}$.

The results for boundary-anchored maps are simpler. Since we are assuming that $f\in {\mathcal{F}}_l$ has a positive shape, the boundary conditions of such a map read: $f\left(a\right)=a$ for any l, and $f\left(b\right)=a$ for l odd, or $f\left(b\right)=b$ for l even. It follows $f^n\left(a\right)=a$, and $f^n\left(b\right)=a$ or $f^n\left(b\right)=b$, respectively, for any $n\ge 1$. To prove the next two lemmas, the following weaker boundary conditions are sufficient, though:

(BC1) 

$f^n\left(a\right)<c_1$, and

(BC2) 

$f^n\left(b\right)<c_1$ if l is odd, or $f^n\left(b\right)>c_l$ if l is even,

for $n\ge 1$. Maps satisfying the confinement conditions (BC1) and (BC2) at the boundary, will be called quasi boundary-anchored maps for obvious reasons.

Lemma 3.4. 

Let $f\in {\mathcal{F}}_l$ be a quasi boundary-anchored map such that

(H1) 

$f\left(c_1\right)>c_l$, and

(H2) 

$f\left(c_l\right)>c_l$ (l odd) or $f\left(c_l\right)<c_1$ (l even).

Then, for all $n\ge 1$,

(a) 

${\xi }_n<{\xi }_{n-1}$, $f^n\left({\xi }_n\right)>c_l$, and $f^n\left({\xi }_n\right)$ is a maximum.

(b) 

(l odd) ${\eta }_n>{\eta }_{n-1}$, $f^n\left({\eta }_n\right)>c_l$, and $f^n\left({\eta }_n\right)$ is a maximum.

(c) 

(l even) ${\eta }_n>{\eta }_{n-1}$, $f^n\left({\eta }_n\right)<c_1$, and $f^n\left({\eta }_n\right)$ is a minimum.

Proof. 

(a) Suppose $f^n\left(a\right)<c_1$ for all $n\ge 1$ (BC1), and $f\left(c_1\right)>c_l$ (H1). Then ${\sigma }_i\left(f\left(a\right)\right)·{\sigma }_i\left(f\left({\xi }_1\right)\right)\equiv {\sigma }_i\left(f\left(a\right)\right)·{\sigma }_i\left(f\left(c_1\right)\right)<0$ for $1\le i\le l$. According to Lemma 3.2 (a) with $i_0=1$, $j_0=l$, and $f\left(a\right)<c_1<f\left(c_1\right)\equiv f\left({\xi }_1\right)$, we have ${\xi }_2<{\xi }_1\equiv c_1$ and $f^2\left({\xi }_2\right)=f\left(c_1\right)>c_l$ is a maximum. By induction it follows that ${\xi }_n<{\xi }_{n-1}$ and $f^n\left({\xi }_n\right)>c_l$ is a maximum for $n\ge 1$.

(b) Suppose l odd, $f^n\left(b\right)<c_1$ for all $n\ge 1$ (BC2), and $f\left(c_l\right)>c_l$ (H2). Then ${\sigma }_i\left(f\left({\eta }_1\right)\right)·{\sigma }_i\left(f\left(b\right)\right)\equiv {\sigma }_i\left(f\left(c_l\right)\right)·{\sigma }_i(f\left(b\right)<0$ for $1\le i\le l$. According to Lemma 3.3 (a) with $i_0=1$, $j_0=l$, and $f\left({\eta }_1\right)\equiv f\left(c_l\right)>c_l>c_1>f\left(b\right)$, we have ${\eta }_2>{\eta }_1\equiv c_l$ and $f^2\left({\eta }_2\right)=f\left(c_1\right)>c_l$ (by H1) is a maximum. By induction it follows that ${\eta }_n>{\eta }_{n-1}$ and $f^n\left({\eta }_n\right)>c_l$ is a maximum for $n\ge 1$.

(c) Suppose l even, $f^n\left(b\right)>c_l$ for all $n\ge 1$ (BC2), and $f\left(c_l\right)<c_1$ (H2). Then ${\sigma }_i\left(f\left({\eta }_1\right)\right)·{\sigma }_i\left(f\left(b\right)\right)\equiv {\sigma }_i\left(f\left(c_l\right)\right)·{\sigma }_i(f\left(b\right)<0$ for $1\le i\le l$. According to Lemma 3.3 (a) with $i_0=1$, $j_0=l$, and $f\left({\eta }_1\right)\equiv f\left(c_l\right)<c_1<c_l<f\left(b\right)$, we have ${\eta }_2>{\eta }_1\equiv c_l$ and $f^2\left({\eta }_2\right)=f\left(c_l\right)<c_1$ is a minimum. By induction it follows that ${\eta }_n>{\eta }_{n-1}$ and $f^n\left({\eta }_n\right)<c_1$ is a minimum for $n\ge 1$. ☐

Lastly, the next lemma is a kind of complementary result to Lemma 3.4.

Lemma 3.5. 

Let $f\in {\mathcal{F}}_l$ be a quasi boundary-anchored map such that

(H1) 

$f\left(c_1\right)<c_1$, and

(H2) 

$f\left(c_l\right)<c_1$ (l odd) or $f\left(c_l\right)>c_l$ (l even).

Then, for all $n\ge 1$,

(a) 

${\xi }_n=c_1$, $f^n\left({\xi }_n\right)<c_1$, and $f^n\left({\xi }_n\right)$ is a maximum.

(b) 

(l odd) ${\eta }_n=c_l$, $f^n\left({\eta }_n\right)<c_1$, and $f^n\left({\eta }_n\right)$ is a maximum.

(c) 

(l even) ${\eta }_n=c_l$, $f^n\left({\eta }_n\right)>c_l$, and $f^n\left({\eta }_n\right)$ is a minimum.

Proof. 

(a) Suppose $f^n\left(a\right)<c_1$ for all $n\ge 1$ (BC1), and $f\left(c_1\right)<c_1$ (H1). Then $f^n\left(c_1\right)<c_1$ (i.e., $f^n\left(c_1\right)\in I_1\equiv [a,b)$) for all $n\ge 1$, because f is assumed to be strictly increasing in $I_1$ [Equation (3)]. Therefore, ${\sigma }_i\left(f\left(a\right)\right)·{\sigma }_i\left(f\left({\xi }_1\right)\right)\equiv {\sigma }_i\left(f\left(a\right)\right)·{\sigma }_i\left(f\left(c_1\right)\right)\ge 0$ for $1\le i\le l$. According to Lemma 3.2 (b) with $n=1$, we have ${\xi }_2={\xi }_1\equiv c_1$, and $f^2\left({\xi }_2\right)=f^2\left(c_1\right)<c_1$ is a maximum because $f\left({\xi }_1\right)\equiv f\left(c_1\right)$ is a maximum [Equation (6)] and $f\left(c_1\right)\in I_1$. By induction it follows that ${\xi }_n=c_1$ and $f^n\left({\xi }_n\right)=f^n\left(c_1\right)<c_1$ is a maximum for $n\ge 1$.

(b) Suppose l odd, $f^n\left(b\right)<c_1$ for all $n\ge 1$ (BC2), and $f\left(c_l\right)<c_1$ (H2). Then $f^n\left(c_l\right)<c_1$ for any $n\ge 1$, because f is assumed to be strictly increasing in $I_1=[a,c_1)$ and $f\left(c_1\right)<c_1$ (H1). Therefore, ${\sigma }_i\left(f\left({\eta }_1\right)\right)·{\sigma }_i\left(f\left(b\right)\right)\equiv {\sigma }_i\left(f\left(c_l\right)\right)·{\sigma }_i\left(f\left(b\right)\right)\ge 0$ for $1\le i\le l$. According to Lemma 3.3 (b) with $n=1$, we have ${\eta }_2={\eta }_1\equiv c_l$, and $f^2\left({\eta }_2\right)=f^2\left(c_l\right)<c_1$ is a maximum because $f\left({\eta }_1\right)\equiv f\left(c_l\right)$ is a maximum [Equation (6) with l odd] and $f\left(c_l\right)\in I_1$. By induction it follows that ${\eta }_n=c_l$ and $f^n\left({\eta }_n\right)=f^n\left(c_l\right)<c_1$ is a maximum for $n\ge 1$.

(c) Suppose l even, $f^n\left(b\right)>c_l$ for all $n\ge 1$ (BC2), and $f\left(c_l\right)>c_l$ (H2). Then $f^n\left(c_l\right)>c_l$ for any $n\ge 1$, because f is assumed to be strictly increasing in $I_{l+1}=(c_l,b]$. Therefore, ${\sigma }_i\left(f\left({\eta }_1\right)\right)·{\sigma }_i\left(f\left(b\right)\right)\equiv {\sigma }_i\left(f\left(c_l\right)\right)·{\sigma }_i\left(f\left(b\right)\right)\ge 0$ for $1\le i\le l$. According to Lemma 3.3 (b) with $n=1$, we have ${\eta }_2={\eta }_1\equiv c_l$, and $f^2\left({\eta }_2\right)=f^2\left(c_l\right)>c_l$ is a minimum because $f\left({\eta }_1\right)\equiv f\left(c_l\right)$ is a minimum [Equation (6) with l even] and $f\left(c_l\right)\in I_{l+1}$ ($l+1$ odd). By induction it follows that ${\eta }_n=c_l$ and $f^n\left({\eta }_n\right)=f^n\left(c_l\right)>c_l$ is a minimum for $n\ge 1$. ☐

4. Counting Laps

Given the kneading sequences of a map $f\in {\mathcal{F}}_l$, it is possible to draw qualitatively the graph of $f^n$ for any $n\ge 1$. The procedure to be explained shortly is based on the geometrical meaning of the MMSs, Lemma 2.1, and the auxiliary lemmas 3.1–3.3; see Example 4.2 below for an illustration.

(A) 

Fix $n\ge 1$ and using the transition rules in Table 1, determine the first n terms of the min-max sequences ${\omega }^i$, $1\le i\le l$, from the seeds ${\omega }_1^i=M^{\sigma \left({\gamma }_1^i\right)}$, if i is odd, and ${\omega }_1^i=m^{\sigma \left({\gamma }_1^i\right)}$, if i is even. For the exposition it is convenient to introduce the notation

$${\omega }^0={\left(f^{\nu }\left(a\right)\right)}_{\nu =1}^{\infty },{\omega }^{l+1}={\left(f^{\nu }\left(b\right)\right)}_{\nu =1}^{\infty }$$

(14)

Actually, from ${\omega }_{\nu }^0=f^{\nu }\left(a\right)$ and ${\omega }_{\nu }^{l+1}=f^{\nu }\left(b\right)$ we shall only need their signatures. Remember that $c_0\equiv a$ and $c_{l+1}\equiv b$.

(B) 

Draw two perpendicular axes and divide the vertical axis into n rows corresponding, top to bottom, to the iterates $f^{\nu }$, $1\le \nu \le n$. The horizontal axis represents the interval $[a,b]$. Enter along this axis the labels a, $c_1$, ..., $c_l$ and b, and write column-wise below them, top to bottom, the sequences ${\left(\sigma \left({\omega }_{\nu }^0\right)\right)}_{\nu =1}^n$, ${\left({\omega }_{\nu }^1\right)}_{\nu =1}^n$..., ${\left({\omega }_{\nu }^l\right)}_{\nu =1}^n$, and $(\sigma {\left({\omega }_{\nu }^{l+1}\right)}_{\nu =1}^n$, respectively (see Table 2 and Table 3). These columns will be called the $c_0$-, ..., $c_{l+1}$-column, respectively. Leave ample space between these columns to insert further columns as we proceed with the present construction.

(C) 

Proceed now row-wise, say left to right, starting with the $\nu =1$ row. We are going to compare pair-wise the signatures of neighboring symbols.

(C1) 

Consider first the unimodal case ($\sigma \equiv {\sigma }_1)$. If $\sigma \left({\omega }_1^0\right)·\sigma \left({\omega }_1^1\right)<0$, then insert ${\left({\omega }_{\nu }^1\right)}_{\nu =1}^{n-1}$ between the $c_0$- and the $c_1$-column, shifted one row downward (i.e., ${\omega }_{\nu }^1$ is on the $(\nu +1)$-th row). If $\sigma \left({\omega }_1^1\right)·\sigma \left({\omega }_1^2\right)<0$, then insert ${\left({\omega }_{\nu }^1\right)}_{\nu =1}^{n-1}$ between the $c_1$- and the $c_2$-column, shifted again one row downward. Otherwise, no action is taken.

(C2) 

Consider now the multimodal case ($l\ge 2$). If ${\sigma }_i\left({\omega }_1^0\right)·{\sigma }_i\left({\omega }_1^1\right)<0$ for $i_0\le i\le i_0+j_0-1$ ($i_0\in \{1,...,l\}$, $j_0\in \{1,...,l-i_0+1\}$) and ${\sigma }_i\left({\omega }_1^0\right)·{\sigma }_i\left({\omega }_1^1\right)>0$ otherwise, then insert the MMSs ${\left({\omega }_{\nu }^{i_0}\right)}_{\nu =1}^{n-1}$, ..., ${\left({\omega }_{\nu }^{i_0+j_0-1}\right)}_{\nu =1}^{n-1}$ between the $c_0$- and the $c_1$-column, shifted one row downward. Otherwise, no action is taken. Furthermore, if $\sigma \left({\omega }_1^0\right)<\sigma \left({\omega }_1^1\right)$ (i.e., $f\left(x\right)$ is increasing in the lap $(c_0,c_1)$), then the MMSs ${\omega }^{i_0}$, ..., ${\omega }^{i_0+j_0-1}$ are inserted in exactly that order. If $\sigma \left({\omega }_1^0\right)>\sigma \left({\omega }_1^1\right)$ (i.e., $f\left(x\right)$ is decreasing in the lap $(c_0,c_1)$), then the MMSs ${\omega }^{i_0}$, ..., ${\omega }^{i_0+j_0-1}$ are inserted in the reversed order: ${\omega }^{i_0+j_0-1}$, ..., ${\omega }^{i_0}$. Repeat this procedure with all remaining pairs of neighboring symbols on row $\nu =1$.

(D) 

Apply the procedure explained in (C) to the rows $\nu =2,...,n$. At the end, row n exhibits the extrema of $f^n$ in $[a,b]$.

Remark 4.1. 

With regard to (C2) and (D), the order of $\sigma \left({\omega }_{\nu }^k\right)$ and $\sigma \left({\omega }_{\nu }^{k+1}\right)$ coincides with the order of ${\sigma }_i\left({\omega }_{\nu }^k\right)$ and ${\sigma }_i\left({\omega }_{\nu }^{k+1}\right)$ for any $i\in \{i_0,...,i_0+j_0-1\}$. In the case $k=0$ and $\nu =1$, $\sigma \left({\omega }_1^0\right)<\sigma \left({\omega }_1^1\right)$ holds because we are assuming that f has a positive shape. Nonetheless we consider also the possibility $\sigma \left({\omega }_1^0\right)>\sigma \left({\omega }_1^1\right)$ in (C2) to explain the general procedure in further steps.

In order to bring clarity into the notation, we stick in the sequel to the above usage: n and the Greek letters $\nu ,\mu ,\kappa ,\tau$ (mostly as subindices, and belonging to $\mathbb{N}$ or ${\mathbb{N}}_0$) will refer to map iterations, while the Latin letters $i,j,k,p,q$ (mostly as upper indices, and belonging to $\{1,...,l\}$) will refer to the critical points.

Example 4.2. 

The cubic polynomial

$$f\left(x\right)=9.375x^3-15.4688x^2+6.75x+0.1,$$

(15)

defines on $I=[0,1]$ a bimodal map with a local maximum at $c_1=0.3$ ($f\left(c_1\right)=0.985938$) and a local minimum at $c_2=0.8$ ($f\left(c_2\right)=0.4$). Figure 1 shows that

$$\begin{array}{ccc}\hfill {\omega }^1& =& (M^{++},M^{+-},m^{+-},M^{++},...)\hfill \\ \hfill {\omega }^2& =& (m^{+-},M^{++},M^{+-},m^{+-},...)\hfill \end{array}$$

Figure 1. Graphs of f, $f^2$, $f^3$, and $f^4$ for the bimodal map (15).

Figure 1. Graphs of f, $f^2$, $f^3$, and $f^4$ for the bimodal map (15).

The first four components of both MMSs have been written on the corresponding column of Table 2 (for $0\le x\le c_1)$ and Table 3 (for $c_1\le x\le 1)$, respectively. The data $\sigma \left({\omega }_{\nu }^0\right)$ and $\sigma \left({\omega }_{\nu }^3\right)$, $1\le \nu \le 4$, appear on the $c_0$- and $c_3$-column, respectively. The additional labels $x_{r,s}$ stand for the critical points of $f^r$. The distribution of the critical points and values of $f^n$, $1\le n\le 4$, will emerge as we apply the procedure (A)–(D) to this particular map. The information about the critical points comprises their number and relative position (or ordering) in the interval $[a,b]$; the corresponding critical values are located up to the precision set by the partition $\mathcal{P}=\{I_1,c_1,I_{2,}...,c_l,I_{l+1}\}$. The details are as follows.

1.

Since ${\sigma }_1\left({\omega }_1^0\right)·{\sigma }_1\left({\omega }_1^1\right)<0$, ${\sigma }_2\left({\omega }_1^0\right)·{\sigma }_2\left({\omega }_1^1\right)<0$, and $\sigma \left({\omega }_1^0\right)=(-,-)<(+,+)=\sigma \left({\omega }_1^1\right)$, we insert ${\omega }^1$ and ${\omega }^2$, beginning on row $\nu =2$, in the given order: ${\omega }^1$ at $x_{2,1}$, ${\omega }^2$ at $x_{2,2}$, with $c_0<x_{2,1}<x_{2,2}<c_1$ (Rule C2). There is only place for the first three components.

2.

Since ${\sigma }_1\left({\omega }_1^1\right)·{\sigma }_1\left({\omega }_1^2\right)>0$, and ${\sigma }_2\left({\omega }_1^1\right)·{\sigma }_2\left({\omega }_1^2\right)<0$, we insert and shift ${\omega }^2$ at $x_{2,3}$, $c_1<x_{2,3}<c_2$.

3.

To complete the first row, we observe that ${\sigma }_1\left({\omega }_1^2\right)·{\sigma }_1\left({\omega }_1^3\right)>0$ and ${\sigma }_2\left({\omega }_1^2\right)·{\sigma }_2\left({\omega }_1^3\right)>0$, so no action is taken. This means that no column right of the $c_2$-column will start on row $\nu =2$. Note that the leftmost critical point of $f^2$ is ${\xi }_2=x_{2,1}$, $f^2\left({\xi }_2\right)$ being a $(+,+)$-maximum, and that the rightmost critical point of $f^2$ is ${\eta }_2=c_2$, $f^2\left({\eta }_2\right)$ being also a $(+,+)$-maximum.

4.

The construction proceeds further along these simple lines. Once the νth row has been completely worked out, the qualitative structure of maxima and minima of $f^{\nu +1}$ emerges on the next row; compare Table 2 and Table 3 with Figure 1. Note that ${\xi }_3={\xi }_4=x_{3,1}$, and ${\eta }_3=x_{3,4}$, ${\eta }_4=x_{4,5}$. We conclude that

$${\ell }_1=3,{\ell }_2=6,{\ell }_3=10,{\ell }_4=15$$

where ${\ell }_n$ is the lap number of $f^n$.

Table 2. Extrema of $f^{\nu }$, $1\le \nu \le 4$, for the map (15), in the interval $[a,c_1]$.

ν	$c_0$	$x_{3,1}$	$x_{2,1}$	$x_{3,2}$	$x_{4,1}$	$x_{2,2}$	$x_{4,2}$	$c_1$
1	$--$							$M^{++}$
2	$+-$		$M^{++}$			$m^{+-}$		$M^{+-}$
3	$+-$	$m^{+-}$	$M^{+-}$	$m^{+-}$		$M^{++}$		$m^{+-}$
4	$+-$	$M^{++}$	$m^{+-}$	$M^{++}$	$m^{+-}$	$M^{+-}$	$m^{+-}$	$M^{++}$

Table 2. Extrema of $f^{\nu }$, $1\le \nu \le 4$, for the map (15), in the interval $[a,c_1]$.

ν	$c_0$	$x_{3,1}$	$x_{2,1}$	$x_{3,2}$	$x_{4,1}$	$x_{2,2}$	$x_{4,2}$	$c_1$
1	$--$							$M^{++}$
2	$+-$		$M^{++}$			$m^{+-}$		$M^{+-}$
3	$+-$	$m^{+-}$	$M^{+-}$	$m^{+-}$		$M^{++}$		$m^{+-}$
4	$+-$	$M^{++}$	$m^{+-}$	$M^{++}$	$m^{+-}$	$M^{+-}$	$m^{+-}$	$M^{++}$

Table 3. Extrema of $f^{\nu }$, $1\le \nu \le 4$, for the map (15), in the interval $[c_1,b]$.

ν	$c_1$	$x_{4,3}$	$x_{2,3}$	$x_{4,4}$	$x_{3,3}$	$c_2$	$x_{3,4}$	$x_{4,5}$	$c_3$
1	$M^{++}$					$m^{+-}$			$+-$
2	$M^{+-}$		$m^{+-}$			$M^{++}$			$+-$
3	$m^{+-}$		$M^{++}$		$m^{+-}$	$M^{+-}$	$m^{+-}$		$++$
4	$M^{++}$	$m^{+-}$	$M^{+-}$	$m^{+-}$	$M^{++}$	$m^{+-}$	$M^{++}$	$m^{+-}$	$+-$

Table 3. Extrema of $f^{\nu }$, $1\le \nu \le 4$, for the map (15), in the interval $[c_1,b]$.

ν	$c_1$	$x_{4,3}$	$x_{2,3}$	$x_{4,4}$	$x_{3,3}$	$c_2$	$x_{3,4}$	$x_{4,5}$	$c_3$
1	$M^{++}$					$m^{+-}$			$+-$
2	$M^{+-}$		$m^{+-}$			$M^{++}$			$+-$
3	$m^{+-}$		$M^{++}$		$m^{+-}$	$M^{+-}$	$m^{+-}$		$++$
4	$M^{++}$	$m^{+-}$	$M^{+-}$	$m^{+-}$	$M^{++}$	$m^{+-}$	$M^{++}$	$m^{+-}$	$+-$

We call the MM-table of f a table constructed following the rules (A)–(D), as exemplified in Table 2 and Table 3. This construction provides the basic tools to derive our algorithm for the lap number ${\ell }_n$ (Theorem 5.3 below).

5. The Main Result

Given $f\in {\mathcal{F}}_l$, let ${\ell }_{\nu }$ denote the lap number of $f^{\nu }$, and $e_{\nu }$ the number of local extrema (or critical points) of $f^{\nu }$, with $\nu \ge 1$. Since $f^{\nu }$ is continuous and piecewise monotone, the laps are separated by critical points, hence the relation,

$${\ell }_{\nu }=e_{\nu }+1$$

(16)

holds. In particular,

$$e_0=0,\text{and}{\ell }_0=1$$

(17)

since $f^0$, the identity, is monotonically strictly increasing, and

$$e_1=l,\text{and}{\ell }_1=l+1$$

(18)

Furthermore, let $s_{\nu }^i$, $1\le i\le l$, stand for the number of interior simple zeros of $f^{\nu }\left(x\right)-c_i$, $\nu \ge 0$, i.e., solutions of $x-c_i=0$ ($\nu =0$), or (ii) solutions of $f^{\nu }\left(x\right)=c_i$, with $x\in (a,b)$, with $f^{\mu }\left(x\right)\ne c_i$ for $0\le \mu \le \nu -1$, and $f^{\nu \prime }\left(x\right)\ne 0$ ($\nu \ge 1$). Geometrically $s_{\nu }^i$ is the number of transversal intersections in the Cartesian plane $(x,y)$ of the curve $y=f^{\nu }\left(x\right)$ and the straight line $y=c_i$, over the interval $(a,b)$. Note that

$$s_0^i=1,\text{and}0\le s_1^i\le l+1\equiv s_{1,max}^i$$

(19)

for all i.

To streamline the notation in the forthcoming results, set

$$s_{\nu }=\sum _{i=1}^l{s}_{\nu }^i$$

(20)

for $\nu \ge 0$. In particular,

$$s_0=\sum _{i=1}^l{s}_0^i=l$$

(21)

Lemma 5.1. 

Let $f\in {\mathcal{F}}_l$. Then, for $\nu \ge 1$,

$$e_{\nu }=e_{\nu -1}+s_{\nu -1}$$

(22)

Proof. 

For $\nu =1$, Equation (22) spells out $e_1=e_0+s_0=l$ on account of (17) and (21), which holds true [see (18)].

For $\nu \ge 2$, use the fact that $e_{\nu }$ equals the number of sign changes of $f^{\nu \prime }$. Then, Equation (22) follows from the relation $f^{\nu \prime }\left(x\right)=f^{\prime }\left(f^{\nu -1}\left(x\right)\right)f^{\nu -1\prime }\left(x\right)$. Note that the x’s with $f^{\nu -1}\left(x\right)=c_i$ and $f^{\nu -1\prime }\left(x\right)=0$ are counted only once (by $e_{\nu -1}$), since they are not simple zeros of $f^{\nu -1}\left(x\right)-c_i=0$. ☐

From (16) and (22) we get

$${\ell }_{\nu }-{\ell }_{\nu -1}=e_{\nu }-e_{\nu -1}=s_{\nu -1}$$

(23)

Addition of $e_{\nu }-e_{\nu -1}=s_{\nu -1}$ for $\nu =1,...,n$ ($e_0=0$) leads to

$$e_n=\sum _{\nu =0}^{n-1}{s}_{\nu }$$

(24)

where $n\ge 1$.

Consider fixed but otherwise arbitrary indices $i\in \{1,...,l\}$ and $\nu \ge 1$. The following two observations are trivial: (i) the upper bound $s_{\nu ,max}^i\equiv$$e_{\nu }+1$ of $s_{\nu }^i$ corresponds to the case in which the graph of $f^{\nu }$ crosses the ith critical line $y=c_i$ on every lap; (ii) the row ν of the MM-table of $f\in {\mathcal{F}}_l$ contains alternating maxima and minima, i.e., alternating symbols $m^{\sigma }$ and $M^{{\sigma }^{\prime }}$ corresponding to the graph points, say, $(x_{r,s},f^{\nu }\left(x_{r,s}\right))$ and $(x_{r^{\prime },s^{\prime }},f^{\nu }\left(x_{r^{\prime },s^{\prime }}\right))$, respectively. If ${\sigma }_i·{\sigma }_i^{\prime }<0$, then the curve $y=f^{\nu }\left(x\right)$ joining the corresponding extrema crosses the critical line $y=c_i$. If, otherwise, ${\sigma }_i·{\sigma }_i^{\prime }\ge 0$, then one of the two symbols involved is necessarily a “bad” symbol, to wit: (i) $m^{\sigma }$ with ${\sigma }_i\in \{0,+\}$, so as the curve $y=f^{\nu }\left(x\right)$ does not cross the ith critical line on the lap $(x_{r,s},x_{r^{\prime },s^{\prime }})$, or (ii) $M^{{\sigma }^{\prime }}$ with ${\sigma }_i^{\prime }\in \{-,0\}$, so as the curve $y=f^{\nu }\left(x\right)$ does not cross either the ith critical line on the same lap. Call

$${\mathcal{B}}^i=\{M^{(...,{\sigma }_i=-,...)},M^{(...,{\sigma }_i=0,...)},m^{(...,{\sigma }_i=0,...)},m^{(...,{\sigma }_i=+,...)}\}$$

(25)

the set of bad symbols or types with respect to the ith critical line. Moreover note that if a bad symbol appears on a column other than the ${\xi }_{\nu }$- or ${\eta }_{\nu }$-column, then the same conclusion concerning the zeros of $f^{\nu }\left(x\right)-c_i$ applies to the two laps of $y=f^{\nu }\left(x\right)$ left and right of corresponding extremum. And if a bad symbol appears on the ${\xi }_{\nu }$- and/or ${\eta }_{\nu }$-column, then there is no zero of $f^{\nu }\left(x\right)-c_i$ in $(a,{\xi }_{\nu })$ and/or $({\eta }_{\nu },b)$.

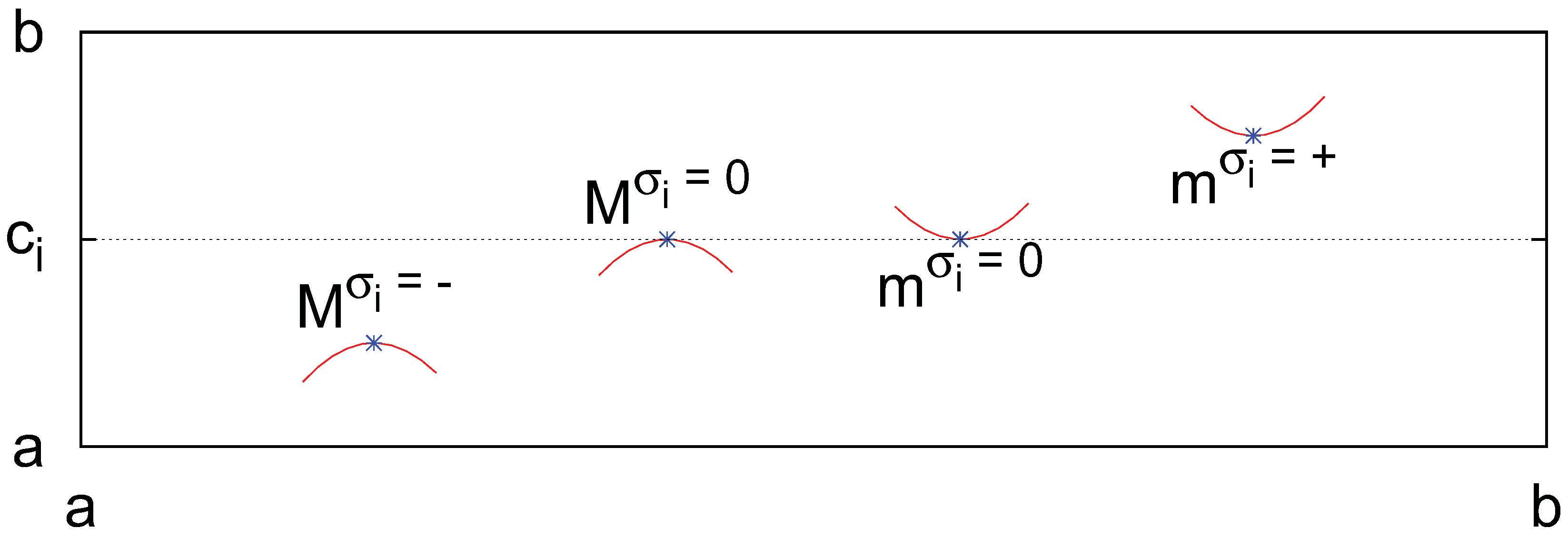
Figure 2 illustrates the geometrical meaning of a bad symbol ${\omega }_{\nu }^i\in {\mathcal{B}}^i$: The branches of the parabolic approximation to a local extrema $f^{\nu }\left(x\right)$ whose type is a bad symbol point away from the critical line $y=c_i$. It is easy to check that

$$\left|{\mathcal{B}}^i\right|=2l+2$$

For example, for $l=2$

$$\begin{array}{ccc}\hfill {\mathcal{B}}^1& =& \{M^{(-,-)},M^{(0,-)},m^{(0,-)},m^{(+,-)},m^{(+,0)},m^{(+,+)}\}\hfill \\ \hfill {\mathcal{B}}^2& =& \{M^{(-,-)},M^{(0,-)},M^{(+,-)},M^{(+,0)},m^{(+,0)},m^{(+,+)}\}\hfill \end{array}$$

If ${\omega }_{\nu }^i\notin {\mathcal{B}}^i$ we say that ${\omega }_{\nu }^i$ is a good symbol with respect to the ith critical line. Since there are $2l+1$ symbols $m^{\sigma }$ and $2l+1$ symbols $M^{\sigma }$, the number of good symbols with respect to the ith critical line is $(4l+2)-(2l+2)=2l$.

Figure 2. Geometrical meaning of the bad symbols (25).

Figure 2. Geometrical meaning of the bad symbols (25).

Therefore, the equality $s_{\nu }^i=e_{\nu }+1\equiv s_{\nu ,max}^i$ is only possible if the row ν in the MM-table of $f\in {\mathcal{F}}_l$ contains only good symbols with respect to the critical line $y=c_i$. Indeed, we have just seen that each bad symbol on row ν subtracts two simple zeros (solutions of $f^{\nu }\left(x\right)-c_i=0$, $f^{\nu \prime }\left(x\right)\ne 0$) from $s_{\nu ,max}^i$. But that condition is not sufficient. It could also happen that the leftmost extremum $f^{\nu }\left({\xi }_{\nu }\right)$ is of good type, but $f^{\nu }\left(x\right)-c_i$ has no zero in the interval $(a,{\xi }_{\nu })$ because ${\sigma }_i\left(f^{\nu }\left(a\right)\right)·{\sigma }_i\left(f^{\nu }\left({\xi }_{\nu }\right)\right)\ge 0$, i.e., the graph points $({\xi }_{\nu },f^{\nu }\left({\xi }_{\nu }\right))$ and $(a,f^{\nu }\left(a\right))$ are both above or both below the critical line $y=c_i$. Of course, a similar consideration holds for the rightmost extremum $f^{\nu }\left({\eta }_{\nu }\right)$ and $f^{\nu }\left(b\right)$ too.

All these facts can be encapsulated in the relation

$$s_{\nu }^i=e_{\nu }+1-2b_{\nu }^i-{\alpha }_{\nu }^i-{\beta }_{\nu }^i$$

(26)

where $b_{\nu }^i$ is the number of symbols from the bad set ${\mathcal{B}}^i$ and

$$\begin{array}{c}{\alpha }_{\nu }^i=\left\{\begin{array}{cc}\hfill 1& \text{if}{f}^{\nu }\left({\xi }_{\nu }\right)\notin {\mathcal{B}}^i\text{but}{\sigma }_i\left(f^{\nu }\left(a\right)\right)·{\sigma }_i\left(f^{\nu }\left({\xi }_{\nu }\right)\right)\ge 0\hfill \\ \hfill 0& \text{otherwise}\hfill \end{array}\right.\hfill \\ {\beta }_{\nu }^i=\left\{\begin{array}{cc}\hfill 1& \text{if}{f}^{\nu }\left({\eta }_{\nu }\right)\notin {\mathcal{B}}^i\text{but}{\sigma }_i\left(f^{\nu }\left(b\right)\right)·{\sigma }_i\left(f^{\nu }\left({\eta }_{\nu }\right)\right)\ge 0\hfill \\ \hfill 0& \text{otherwise}\hfill \end{array}\right.\hfill \end{array}$$

(27)

Before using the previous results to formulate a recursive procedure to calculate the lap number ${\ell }_n$, we need to relate the symbols ${\omega }_n^i$ on the ${\xi }_{\nu }$- and ${\eta }_{\nu }$-columns to the critical values $f^{\nu }\left({\xi }_{\nu }\right)$ and $f^{\nu }\left({\eta }_{\nu }\right)$.

Remember that in the construction of the MM-table of f, we may encounter two situations in the intervals $(a,{\xi }_{\nu })$ (a similar discussion holds for the intervals $({\eta }_{\nu },b)$).

(S1) 

If $\nu \ge 2$, ${\sigma }_i\left(f^{\nu -1}\left(a\right)\right)·{\sigma }_i\left(f^{\nu -1}\left({\xi }_{\nu -1}\right)\right)<0$ for $i_0\le i\le i_0+j_0-1$, and ${\sigma }_i\left(f^{\nu -1}\left(a\right)\right)·{\sigma }_i(f^{\nu -1}\left({\xi }_{\nu -1}\right)\ge 0$ otherwise, then ${\xi }_{\nu }<{\xi }_{\nu -1}$ [Lemma 3.2 (a)], and we write down ${\omega }^{i_0}$ (if ${\sigma }_{i_0}\left(f^{\nu -1}\left(a\right)\right)<{\sigma }_{i_0}(f^{\nu -1}\left({\xi }_{\nu -1}\right)$) or ${\omega }^{i_0+j_0-1}$ (if ${\sigma }_{i_0}\left(f^{\nu -1}\left(a\right)\right)>{\sigma }_{i_0}(f^{\nu -1}\left({\xi }_{\nu -1}\right)$) on the ${\xi }_{\nu }$-column, beginning at row ν. To address both possibilities in the present discussion, denote by ${\omega }^{p\left(\nu \right)}$ the sequence on the ${\xi }_{\nu }$-column (note $p\left(\nu \right)=i_0=i_0+j_0-1$ if $j_0=1$).

(S2) 

On the other hand, suppose ${\sigma }_i\left(f^{\nu -1}\left(a\right)\right)·{\sigma }_i\left(f^{\nu -1}\left({\xi }_{\nu -1}\right)\right)\ge 0$ for all $i=1,...,l$, and ${\xi }_{\nu -1}<{\xi }_{\nu -2}$ (or ${\xi }_{\nu -1}=c_1$ if $\nu =2$). In this case ${\xi }_{\nu }={\xi }_{\nu -1}$ [Lemma 3.2 (b)]. If again ${\sigma }_i\left(f^{\nu }\left(a\right)\right)·{\sigma }_i\left(f^{\nu }\left({\xi }_{\nu }\right)\right)\ge 0$ for all i, then ${\xi }_{\nu +1}={\xi }_{\nu }$. In general, if this happens τ consecutive times (i.e., for $f^{\nu -1},...,f^{\nu +\tau -2}$), then (i) ${\xi }_{\nu -1}={\xi }_{\nu }=...={\xi }_{\nu +\tau -1}$, and (ii) the leftmost extrema $f^{\nu }\left({\xi }_{\nu }\right),...,f^{\nu +\tau -1}\left({\xi }_{\nu +\tau -1}\right)$ are of type ${\omega }_2^{p(\nu -1)},...,{\omega }_{\tau +1}^{p(\nu -1)}$, respectively (see Table 2).

In order to accommodate all these possibilities in the notation, ${\omega }_{\lambda \left(\nu \right)}^{p\left(\nu \right)}$ will denote the $(\nu ,{\xi }_{\nu })$-entry in the MM-table of f, i.e., the symbol on the row ν of the ${\xi }_{\nu }$-column. Analogously, ${\omega }_{\rho \left(\nu \right)}^{q\left(\nu \right)}$ will designate the $(\nu ,{\eta }_{\nu })$-entry in the MM-table of f. From (27), (S1) and (S2), it follows

$$\begin{array}{c}{\alpha }_{\nu }^i=\left\{\begin{array}{cc}\hfill 1& \text{if}{\sigma }_i\left(f^{\nu }\left(a\right)\right)·{\sigma }_i\left({\omega }_{\lambda \left(\nu \right)}^{p\left(\nu \right)}\right)\ge 0\text{and}{\omega }_{\lambda \left(\nu \right)}^{p\left(\nu \right)}\notin {\mathcal{B}}^i\hfill \\ \hfill 0& \text{otherwise}\hfill \end{array}\right.\hfill \\ {\beta }_{\nu }^i=\left\{\begin{array}{cc}\hfill 1& \text{if}{\sigma }_i\left(f^{\nu }\left(b\right)\right)·{\sigma }_i\left({\omega }_{\rho \left(\nu \right)}^{q\left(\nu \right)}\right)\ge 0\text{and}{\omega }_{\rho \left(\nu \right)}^{q\left(\nu \right)}\notin {\mathcal{B}}^i\hfill \\ \hfill 0& \text{otherwise}\hfill \end{array}\right.\hfill \end{array}$$

(28)

where $p\left(1\right)=1$, $q\left(1\right)=l$, and for $\nu \ge 2$,

$$\begin{array}{ccc}\hfill p\left(\nu \right)& =& \left\{\begin{array}{cc}{p}_1& \text{if}{\sigma }_i\left(f^{\nu -1}\left(a\right)\right)·{\sigma }_i\left({\omega }_{\lambda (\nu -1)}^{p(\nu -1)}\right)<0\text{for}{p}_1\le i\le p_2\text{,}\text{and}{\omega }_{\lambda (\nu -1)}^{p(\nu -1)}=M^{*}\hfill \\ p_2& \text{if}{\sigma }_i\left(f^{\nu -1}\left(a\right)\right)·{\sigma }_i\left({\omega }_{\lambda (\nu -1)}^{p(\nu -1)}\right)<0\text{for}{p}_1\le i\le p_2\text{,}\text{and}{\omega }_{\lambda (\nu -1)}^{p(\nu -1)}=m^{*}\hfill \\ p(\nu -1)& \text{otherwise}\hfill \end{array}\right.\hfill \\ \hfill q\left(\nu \right)& =& \left\{\begin{array}{cc}{q}_1& \text{if}{\sigma }_i\left(f^{\nu -1}\left(b\right)\right)·{\sigma }_i\left({\omega }_{\rho (\nu -1)}^{q(\nu -1)}\right)<0\text{for}{q}_1\le i\le q_2\text{,}\text{and}{\omega }_{\rho (\nu -1)}^{q(\nu -1)}=M^{*}\hfill \\ q_2& \text{if}{\sigma }_i\left(f^{\nu -1}\left(b\right)\right)·{\sigma }_i\left({\omega }_{\rho (\nu -1)}^{q(\nu -1)}\right)<0\text{for}{q}_1\le i\le q_2\text{,}\text{and}{\omega }_{\rho (\nu -1)}^{q(\nu -1)}=m^{*}\hfill \\ q(\nu -1)& \text{otherwise}\hfill \end{array}\right.\hfill \end{array}$$

(29)

with $1\le p_1\le p_2\le l$, and $1\le q_1\le q_2\le l$. Here $p_1,q_1$ [resp. $p_2,q_2$] are meant to be the smallest [resp. greatest] values of the index i for which the corresponding inequalities hold, and $M^{*}$ [resp. $m^{*}$] stands for a maximum [resp. minimum] of any signature. The functions $\lambda \left(\nu \right)$, $\rho \left(\nu \right)$ are recursively calculated as follows: $\lambda \left(1\right)=\rho \left(1\right)=1$, and for $\nu \ge 2$,

$$\begin{array}{c}\lambda \left(\nu \right)=\left\{\begin{array}{cc}1& \text{if}{\sigma }_i\left(f^{\nu -1}\left(a\right)\right)·{\sigma }_i\left({\omega }_{\lambda (\nu -1)}^{p(\nu -1)}\right)<0\text{for}\text{some}i\hfill \\ \lambda (\nu -1)+1& \text{if}{\sigma }_i\left(f^{\nu -1}\left(a\right)\right)·{\sigma }_i\left({\omega }_{\lambda (\nu -1)}^{p(\nu -1)}\right)\ge 0\text{for}\text{all}i\hfill \end{array}\right.\hfill \\ \rho \left(\nu \right)=\left\{\begin{array}{cc}1& \text{if}{\sigma }_i\left(f^{\nu -1}\left(b\right)\right)·{\sigma }_i\left({\omega }_{\rho (\nu -1)}^{q(\nu -1)}\right)<0\text{for}\text{some}i\hfill \\ \rho (\nu -1)+1& \text{if}{\sigma }_i\left(f^{\nu -1}\left(b\right)\right)·{\sigma }_i\left({\omega }_{\rho (\nu -1)}^{q(\nu -1)}\right)\ge 0\text{for}\text{all}i\hfill \end{array}\right.\hfill \end{array}$$

(30)

In the unimodal case ($l=1$), Equations (28)–(30) simplify to (37)–(38), Section 6.

Example 5.2. 

(Cont’d) Let us illustrate the above formulas with the bimodal map (15) considered in Example 4.2. The following values in Table 4 can be calculated with data from Table 2 and Table 3.

Table 4. Values of ${\alpha }_{\nu }^i$ and ${\beta }_{\nu }^i$ for the bimodal map (15).

ν	$p\left(\nu \right)$	$\lambda \left(\nu \right)$	${\alpha }_{\nu }^1$	${\alpha }_{\nu }^2$	$q\left(\nu \right)$	$\rho \left(\nu \right)$	${\beta }_{\nu }^1$	${\beta }_{\nu }^2$
1	1	1	0	0	2	1	0	1
2	1	1	1	0	2	2	1	0
3	2	1	0	1	2	1	0	0
4	2	2	1	0	2	1	0	1

Table 4. Values of ${\alpha }_{\nu }^i$ and ${\beta }_{\nu }^i$ for the bimodal map (15).

ν	$p\left(\nu \right)$	$\lambda \left(\nu \right)$	${\alpha }_{\nu }^1$	${\alpha }_{\nu }^2$	$q\left(\nu \right)$	$\rho \left(\nu \right)$	${\beta }_{\nu }^1$	${\beta }_{\nu }^2$
1	1	1	0	0	2	1	0	1
2	1	1	1	0	2	2	1	0
3	2	1	0	1	2	1	0	0
4	2	2	1	0	2	1	0	1

Let us understand the geometrical meaning of the values of, say, row $\nu =3$ in view of the MM-table of f, Table 2 and Table 3.

• $p\left(3\right)=2$ and $\lambda \left(3\right)=1$ because the leftmost column beginning at or intersecting the row $\nu =3$ (the $x_{3,1}$-column) has the symbol $m^{+-}={\omega }_1^2\equiv {\omega }_{\lambda \left(3\right)}^{p\left(3\right)}$ on row $\nu =3$.
• ${\alpha }_3^1=0$ because ${\omega }_{\lambda \left(3\right)}^{p\left(3\right)}=m^{+-}$$\in {\mathcal{B}}^1$, i.e., it is a bad symbol with respect to the critical line $y=c_1$ (so the lack of a zero of $f^3\left(x\right)-c_1$ in the interval $(a,{\xi }_3)$ is already accounted for in the term $2b_3^1$ of Equation (26)). On the other hand, ${\alpha }_3^2=1$ because ${\omega }_{\lambda \left(3\right)}^{p\left(3\right)}=m^{+-}$$\notin {\mathcal{B}}^2$, i.e., it is a good symbol with respect to the critical line $y=c_2$ but $f^3\left(a\right)<c_2$ (see the second sign on row $\nu =3$ of the $c_0$-column), so $f^3\left(x\right)-c_2$ has no zero in the interval $(a,{\xi }_3)$.
• $q\left(3\right)=2$ and $\rho \left(3\right)=1$ because the rightmost column beginning at or intersecting the row $\nu =3$ (i.e., the $x_{3,4}$-column) has the symbol $m^{+-}={\omega }_1^2\equiv {\omega }_{\rho \left(3\right)}^{q\left(3\right)}$ on row $\nu =3$.
• ${\beta }_3^1=0$ because ${\omega }_{\rho \left(3\right)}^{q\left(3\right)}=m^{+-}$$\in {\mathcal{B}}^1$. On the other hand, ${\beta }_3^2=0$ because ${\omega }_{\rho \left(3\right)}^{q\left(3\right)}=m^{+-}$ is a good symbol with respect to the critical line $y=c_2$ and, furthermore, $f^3\left(b\right)>c_2$ (see the second sign on row $\nu =3$ of $c_3$-column), so $f^3\left(x\right)-c_2$ has one zero in the interval $({\eta }_3,b)$.

We can now derive the main result of this paper.

Theorem 5.3. 

Let ${\omega }^i={\left({\omega }_{\nu }^i\right)}_{\nu \ge 1}$, $1\le i\le l$, be the MMSs of $f\in {\mathcal{F}}_l$, and ${\left({\alpha }_{\nu }^i\right)}_{\nu \ge 1}$, ${\left({\beta }_{\nu }^i\right)}_{\nu \ge 1}$ the 0-1 sequences obtained from (28)–(30). Set

$$K_{\nu }^i=\{(k,\kappa ),1\le k\le l,1\le \kappa \le \nu :{\omega }_{\kappa }^k\in {\mathcal{B}}^i\}$$

Then the lap number of $f^n$, $n\ge 1$, is given by

$${\ell }_n=1+\sum _{\nu =0}^{n-1}{s}_{\nu }$$

(31)

where $s_{\nu }={\sum }_{i=1}^l{s}_{\nu }^i$ (20), $s_0^i=1$ (19), and for $\nu \ge 1$,

$$s_{\nu }^i=1+\sum _{\mu =0}^{\nu -1}{s}_{\mu }-2\sum _{(k,\kappa )\in K_{\nu }^i}{s}_{\nu -\kappa }^k-{\alpha }_{\nu }^i-{\beta }_{\nu }^i$$

(32)

Proof. 

Addition of ${\ell }_{\nu }-{\ell }_{\nu -1}=s_{\nu -1}$ (23) for $\nu =1,...,n$ [${\ell }_0=1$ (17)], yields the expression (31).

Let $N_{\nu }^i$ be the number of ${\omega }^i$ sequences that begin at row ν on the MM-table of f, and, as before, let $b_{\nu }^i$ be the number of symbols of ${\mathcal{B}}^i$ on row ν. Then,

$$b_{\nu }^i=\sum _{(k,\kappa )\in K_{\nu }^i}{N}_{\nu -\kappa +1}^k$$

(33)

By Lemma 3.1, $N_{\nu }^i=s_{\nu -1}^i$ for $\nu \ge 2$. Since $N_1^i=1$ and $s_0^i=1$ (19), $1\le i\le l$, we conclude that $N_{\nu }^i=s_{\nu -1}^i$ for $\nu \ge 1$ as well. Upon substitution of this equality and Equation (26) into Equation (33), we obtain

$$s_{\nu }^i=e_{\nu }+1-2\sum _{(k,\kappa )\in K_{\nu }^i}{s}_{\nu -\kappa }^k-{\alpha }_{\nu }^i-{\beta }_{\nu }^i$$

(34)

Finally, use (24) to derive the expression (32). ☐

In view of (31), Equation (32) can be shortened to

$$s_{\nu }^i={\ell }_{\nu }-2\sum _{(k,\kappa )\in K_{\nu }^i}{s}_{\nu -\kappa }^k-{\alpha }_{\nu }^i-{\beta }_{\nu }^i$$

(35)

In particular, ${\ell }_1=l+1$, and $K_1^i=\{(k,1),1\le k\le l:{\omega }_1^k\in {\mathcal{B}}^i\}$, hence ${\sum }_{(k,1)\in K_1^i}{s}_{1-\kappa }^k={\sum }_{(k,1)\in K_1^i}{s}_0^k=\left|K_1^i\right|$ since $s_0^k=1$ for every k (19). Therefore

$$s_1^i=l+1-2\left|K_1^i\right|-{\alpha }_1^i-{\beta }_1^i$$

Example 5.4. 

(Cont’d) Once again let f be the cubic map (15) restricted to the interval $[0,1]$. With the information provided in Example 5.2. and the formulas of Theorem 5.3., we get the following results in Table 5.

Table 5. Lap numbers of the first four iterates of the map (15).

ν	$K_{\nu }^1$	$K_{\nu }^2$	$s_{\nu }^1$	$s_{\nu }^2$	$s_{\nu }$	${\ell }_{\nu }$
1	$\left\{\right(2,1\left)\right\}$	∅	1	2	3	3
2	$\left\{\right(2,1\left)\right\}$	$\left\{\right(1,2\left)\right\}$	0	4	4	6
3	$\left\{\right(2,1),(1,3\left)\right\}$	$\left\{\right(1,2),(2,3\left)\right\}$	0	5	5	10
4	$\left\{\right(2,1),(1,3),(2,4\left)\right\}$	$\left\{\right(1,2),(2,3\left)\right\}$	0	10	10	15

Table 5. Lap numbers of the first four iterates of the map (15).

ν	$K_{\nu }^1$	$K_{\nu }^2$	$s_{\nu }^1$	$s_{\nu }^2$	$s_{\nu }$	${\ell }_{\nu }$
1	$\left\{\right(2,1\left)\right\}$	∅	1	2	3	3
2	$\left\{\right(2,1\left)\right\}$	$\left\{\right(1,2\left)\right\}$	0	4	4	6
3	$\left\{\right(2,1),(1,3\left)\right\}$	$\left\{\right(1,2),(2,3\left)\right\}$	0	5	5	10
4	$\left\{\right(2,1),(1,3),(2,4\left)\right\}$	$\left\{\right(1,2),(2,3\left)\right\}$	0	10	10	15

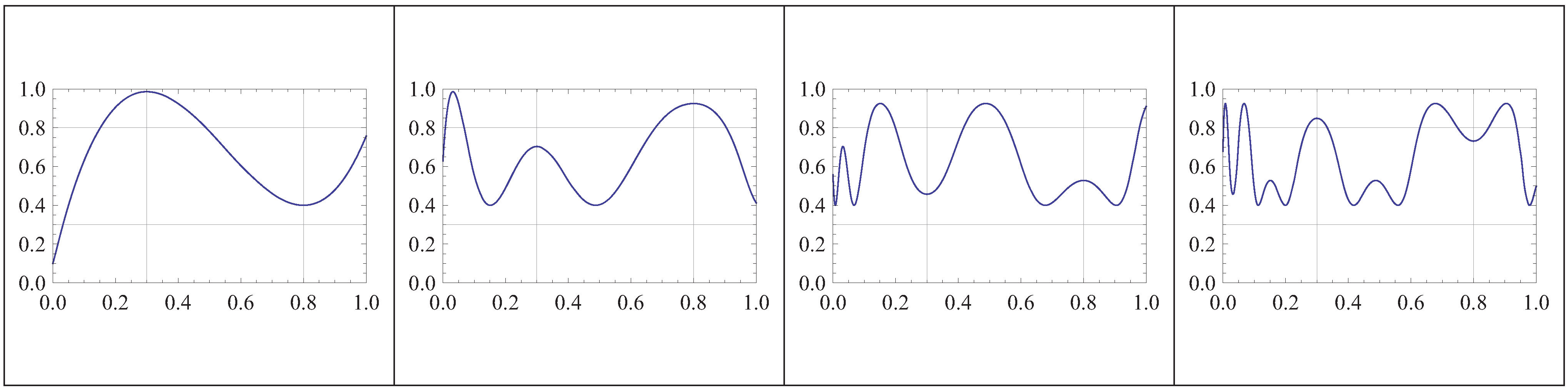
For instance,

$$\begin{array}{ccc}\hfill s_3^1& =& l+1+s_1+s_2-2(s_2^2+s_0^1)-{\alpha }_3^1-{\beta }_3^1\hfill \\ & =& 2+1+3+4-2(4+1)-0-0=0\hfill \\ \hfill s_3^2& =& l+1+s_1+s_2-2(s_1^1+s_0^2)-{\alpha }_3^2-{\beta }_3^2\hfill \\ & =& 2+1+3+4-2(1+1)-1-0=5\hfill \end{array}$$

hence, $s_3=s_3^1+s_3^2=5$. Finally, Equation (31),

$${\ell }_4=1+s_0+s_1+s_2+s_3=1+2+3+4+5=15$$

All these numerical results can be checked at Figure 1.

Two comments are in order at this point.

First, the computation scheme (31) and (32) for the lap number ${\ell }_n$ only involves two ingredients: The first n symbols of the l MMSs of f, and the first n signatures of the itineraries of both endpoints.

Secondly, the number of summations in (31) and (32) for the computation of ${\ell }_n$ is $O\left(n^2\right)$. Moreover, this scheme is almost recursive. Indeed the value of $s_{\nu }^i$ is determined by the values of $s_1^i$, $s_2^i$, ..., $s_{\nu -1}^i$ along with the values of ${\alpha }_{\nu }^i,{\beta }_{\nu }^i\in \{0,1\}$, which have to be calculated anew for each ν. Thus, in the particular case ${\alpha }_{\nu }^i={\beta }_{\nu }^i=0$ for all $i=1,...,l$ and $\nu \ge 1$, the algorithm is not only much simpler but fully recursive.

6. Special Cases

The next two lemmas provide sufficient conditions for all ${\alpha }_{\nu }^i$’s and ${\beta }_{\nu }^i$’s in (32) to vanish. Remember that a map is called quasi boundary-anchored if it satisfies the boundary conditions (BC1) and (BC2) of Section 3. The most prominent instance of quasi boundary-anchored maps are the boundary-anchored ones.

Lemma 6.1. 

Let $f\in {\mathcal{F}}_l$ be a quasi boundary-anchored map such that

(H1) 

$f\left(c_1\right)>c_l$, and

(H2) 

$f\left(c_l\right)>c_l$ (l odd) or $f\left(c_l\right)<c_1$ (l even).

Then $p\left(\nu \right)=1$, $q\left(\nu \right)=l$, $\lambda \left(\nu \right)=1$, $\rho \left(\nu \right)=1$, and

$${\alpha }_{\nu }^i={\beta }_{\nu }^i=0$$

(36)

for all $\nu \ge 1$, $1\le i\le l$.

Proof. 

From Lemma 3.4 (a)–(c) and their corresponding proofs, we conclude the following results.

(a) ${\sigma }_i\left(f^{\nu }\left(a\right)\right)·{\sigma }_i\left(f^{\nu }\left({\xi }_{\nu }\right)\right)<0$, ${\xi }_{\nu }<{\xi }_{\nu -1}$, and

$${\omega }_{\lambda \left(\nu \right)}^{p\left(\nu \right)}={\omega }_1^1=M^{(+,...,+)}\notin {\mathcal{B}}^i$$

[see (25)] for all $\nu \ge 1$, $1\le i\le l.$

(b) ${\sigma }_i\left(f^{\nu }\left(b\right)\right)·{\sigma }_i\left(f^{\nu }\left({\eta }_{\nu }\right)\right)<0$, ${\eta }_{\nu }>{\eta }_{\nu -1}$, and

$${\omega }_{\rho \left(\nu \right)}^{q\left(\nu \right)}={\omega }_1^l=M^{(+,...,+)}\notin {\mathcal{B}}^i$$

for all $\nu \ge 1$, $1\le i\le l$, l odd.

(c) ${\sigma }_i\left(f^{\nu }\left(b\right)\right)·{\sigma }_i\left(f^{\nu }\left({\eta }_{\nu }\right)\right)<0$, ${\eta }_{\nu }>{\eta }_{\nu -1}$, and

$${\omega }_{\rho \left(\nu \right)}^{q\left(\nu \right)}={\omega }_1^l=m^{(-,...,-)}\notin {\mathcal{B}}^i$$

for all $\nu \ge 1$, $1\le i\le l$, l even.

In sum,

$$\left\{\begin{array}{c}{\omega }_{\lambda \left(\nu \right)}^{p\left(\nu \right)}={\omega }_1^1\notin {\mathcal{B}}^i,{\omega }_{\rho \left(\nu \right)}^{q\left(\nu \right)}={\omega }_1^l\notin {\mathcal{B}}^i\hfill \\ {\sigma }_i\left(f^{\nu }\left(a\right)\right)·{\sigma }_i\left(f^{\nu }\left({\xi }_{\nu }\right)\right)<0,\text{ and }{\sigma }_i\left(f^{\nu }\left({\eta }_{\nu }\right)\right)·{\sigma }_i\left(f^{\nu }\left(b\right)\right)<0\hfill \end{array}\right.$$

for all $\nu \ge 1$, and $i\in \{1,...,l\}$. From the definition (28) it follows that all the ${\alpha }_{\nu }^i$’s and ${\beta }_{\nu }^i$’s vanish. ☐

Lemma 3.5 provides a second scenario for the vanishing of all ${\alpha }_{\nu }^i$’s and ${\beta }_{\nu }^i$’s.

Lemma 6.2. 

Let $f\in {\mathcal{F}}_l$ be a quasi boundary-anchored map such that

(H1)

$f\left(c_1\right)<c_1$, and

(H2)

$f\left(c_l\right)<c_1$ (l odd) or $f\left(c_l\right)>c_l$ (l even).

Then $p\left(\nu \right)=1$, $q\left(\nu \right)=l$, $\lambda \left(\nu \right)=\nu$, $\rho \left(\nu \right)=\nu$, and

$${\alpha }_{\nu }^i={\beta }_{\nu }^i=0$$

for all $\nu \ge 1$, $1\le i\le l$.

Proof. 

From Lemma 3.5 (a)–(c) and their corresponding proofs, we conclude the following results.

(a) ${\sigma }_i\left(f^{\nu }\left(a\right)\right)·{\sigma }_i\left(f^{\nu }\left({\xi }_{\nu }\right)\right)\ge 0$, ${\xi }_{\nu }=c_1$, and

$${\omega }_{\lambda \left(\nu \right)}^{p\left(\nu \right)}={\omega }_{\nu }^1=M^{(-,...,-)}\in {\mathcal{B}}^i$$

[check (25)] for all $\nu \ge 1$, $1\le i\le l.$

(b) ${\sigma }_i\left(f^{\nu }\left(b\right)\right)·{\sigma }_i\left(f^{\nu }\left({\eta }_{\nu }\right)\right)\ge 0$, ${\eta }_{\nu }=c_l$, and

$${\omega }_{\rho \left(\nu \right)}^{q\left(\nu \right)}={\omega }_{\nu }^l=M^{(-,...,-)}\in {\mathcal{B}}^i$$

for all $\nu \ge 1$, $1\le i\le l$, l odd.

(c) ${\sigma }_i\left(f^{\nu }\left(b\right)\right)·{\sigma }_i\left(f^{\nu }\left({\eta }_{\nu }\right)\right)\ge 0$, ${\eta }_{\nu }=c_l$, and

$${\omega }_{\rho \left(\nu \right)}^{q\left(\nu \right)}={\omega }_{\nu }^l=m^{(+,...,+)}\in {\mathcal{B}}^i$$

for all $\nu \ge 1$, $1\le i\le l$, l even.

In sum,

$$\left\{\begin{array}{c}{\omega }_{\lambda \left(\nu \right)}^{p\left(\nu \right)}={\omega }_{\nu }^1\in {\mathcal{B}}^i{\omega }_{\rho \left(\nu \right)}^{q\left(\nu \right)}={\omega }_{\nu }^l\in {\mathcal{B}}^i,\hfill \\ {\sigma }_i\left(f^{\nu }\left(a\right)\right)·{\sigma }_i\left(f^{\nu }\left({\xi }_{\nu }\right)\right)\ge 0,\text{ and }{\sigma }_i\left(f^{\nu }\left({\eta }_{\nu }\right)\right)·{\sigma }_i\left(f^{\nu }\left(b\right)\right)\ge 0\hfill \end{array}\right.$$

for all $\nu \ge 1$, and $i\in \{1,...,l\}$. From the definition (28) it follows that all the ${\alpha }_{\nu }^i$’s and ${\beta }_{\nu }^i$’s vanish. ☐

Another nice simplification occurs when the map is unimodal because then $s_n={\sum }_{i=1}^l{s}_n^i=s_n^1$. To make the notation uniform, set ${\omega }_{\nu }\equiv {\omega }_{\nu }^1$, $\mathcal{B}\equiv {\mathcal{B}}^1=\{m^0,m^{+},M^0,M^{-}\}$, $K_n\equiv K_n^1\subset \left\{1\right\}\times \{1,...,l\}$, ${\alpha }_{\nu }\equiv {\alpha }_{\nu }^1$, and ${\beta }_{\nu }\equiv {\beta }_{\nu }^1$ in the unimodal case. Furthermore, for $l=1$ Equations (28)–(30) get abridged to

$$\begin{array}{c}{\alpha }_{\nu }=\left\{\begin{array}{cc}\hfill 1& \text{if}\sigma \left(f^{\nu }\left(a\right)\right)·\sigma \left({\omega }_{\lambda \left(\nu \right)}\right)\ge 0\text{and}{\omega }_{\lambda \left(\nu \right)}\notin \mathcal{B}\hfill \\ \hfill 0& \text{otherwise}\hfill \end{array}\right.\hfill \\ {\beta }_{\nu }=\left\{\begin{array}{cc}\hfill 1& \text{if}\sigma \left(f^{\nu }\left(b\right)\right)·\sigma \left({\omega }_{\rho \left(\nu \right)}\right)\ge 0\text{and}{\omega }_{\rho \left(\nu \right)}\notin \mathcal{B}\hfill \\ \hfill 0& \text{otherwise}\hfill \end{array}\right.\hfill \end{array}$$

(37)

where $\sigma (·)\equiv {\sigma }_1(·)$, $\lambda \left(1\right)=\rho \left(1\right)=1$, and for $\nu \ge 2$,

$$\begin{array}{c}\lambda \left(\nu \right)=\left\{\begin{array}{cc}1& \text{if}\sigma \left(f^{\nu -1}\left(a\right)\right)·\sigma \left({\omega }_{\lambda (\nu -1)}\right)<0\hfill \\ \lambda (\nu -1)+1& \text{if}\sigma \left(f^{\nu -1}\left(a\right)\right)·\sigma \left({\omega }_{\lambda (\nu -1)}\right)\ge 0\hfill \end{array}\right.\hfill \\ \rho \left(\nu \right)=\left\{\begin{array}{cc}1& \text{if}\sigma \left(f^{\nu -1}\left(b\right)\right)·\sigma \left({\omega }_{\rho (\nu -1)}\right)<0\hfill \\ \rho (\nu -1)+1& \text{if}\sigma \left(f^{\nu -1}\left(b\right)\right)·\sigma \left({\omega }_{\rho (\nu -1)}\right)\ge 0\hfill \end{array}\right.\hfill \end{array}$$

(38)

Note that Equation (29) boils down to $p\left(\nu \right)=q\left(\nu \right)=1$ for any $\nu \ge 1$ (as it should, since unimodal maps have only one MMS).

Theorem 6.3 

([16]). Let $\omega ={\left({\omega }_{\nu }\right)}_{\nu \ge 1}$ be the MMS of $f\in {\mathcal{F}}_1$, $\mathcal{B}=\{m^0,m^{+},M^0,M^{-}\}$, and

$$K_n=\{1\le \kappa \le n:{\omega }_{\kappa }\in \mathcal{B}\}$$

If ${\left({\alpha }_{\nu }\right)}_{\nu \ge 1}$, ${\left({\beta }_{\nu }\right)}_{\nu \ge 1}$, are the 0-1 sequences obtained from (37)–(38), then

$${\ell }_{n+1}=2{\ell }_n-2\sum _{\kappa \in K_n}({\ell }_{n+1-\kappa }-{\ell }_{n-\kappa })-{\alpha }_n-{\beta }_n$$

(39)

where $n\ge 1$ and ${\ell }_0=1$ (17).

Proof. 

In the unimodal case, Equation (35) reads

$$s_n={\ell }_n-2\sum _{\kappa \in K_n}{s}_{n-\kappa }-{\alpha }_n-{\beta }_n$$

(40)

Substitution of $s_{\nu }={\ell }_{\nu +1}-{\ell }_{\nu }$ (23) with $\nu =n$ and $\nu =n-\kappa$ into (40), produces (39). ☐

Denote by c the only critical point $c_1$ of $f\in {\mathcal{F}}_1$. Application of Lemma 6.1 ($f\left(c\right)>c$) and Lemma 6.2 ($f\left(c\right)<c$) to Theorem 6.3 yields a further simplification.

Corollary 6.4 

([13,15]). Let $\omega ={\left({\omega }_{\nu }\right)}_{\nu \ge 1}$ be the MMS of a quasi boundary-anchored map $f\in {\mathcal{F}}_1$ (i.e., $f^{\nu }\left(a\right)<c,f^{\nu }\left(b\right)<c$ for all $\nu \ge 1$). Then,

$${\ell }_{n+1}=2{\ell }_n-2\sum _{\kappa \in K_n}({\ell }_{n+1-\kappa }-{\ell }_{n-\kappa })$$

(41)

for $n\ge 1$.

Alternatively, one can set $l=1$ and ${\alpha }_{\nu }^i={\beta }_{\nu }^i=0$ in (31)–(32) to derive, under the assumptions of Corollary 6.4,

$${\ell }_n=1+\sum _{\nu =0}^{n-1}{s}_{\nu }$$

(42)

where $s_0=1$ [see (17)], and

$$s_{\nu }=1+\sum _{\mu =0}^{\nu -1}{s}_{\mu }-2\sum _{\kappa \in K_{\nu }}{s}_{\nu -\kappa }$$

(43)

for $\nu \ge 1$.

As a quick check, observe that if $f\left(c\right)<c$, then $\omega ={\left(M^{-}\right)}^{\infty }$, hence $K_n=\{1,...,n\}$. In this case, (41) collapses to ${\ell }_{n+1}=2{\ell }_0=2$. Likewise, (43) provides $s_{\nu }=0$ for all $\nu \ge 1$, thus ${\ell }_n=1+s_0=2$ by (42).

7. An Algorithm for the Topological Entropy

The logical flow of the algorithm provided by Theorem 5.3 for the calculation of ${\ell }_n$ is as follows. We use the notation ‘$A⟶$Equation (n)$⟶B$’ to indicate that data B is computed from data A via the formula given in Equation (n).

• Preprocessing. Calculate the MMSs of $f\in {\mathcal{F}}_l$, ${\left({\omega }_{\nu }^k\right)}_{1\le \nu \le n-1}$ for $0\le k\le l+1$ [remember the convention (14)]. The sequences ${\left({\omega }_{\nu }^i\right)}_{1\le \nu \le n-1}$, $1\le i\le l$, readily follow from the initial symbols ${\omega }_1^i$ and the kneading sequences ${\gamma }^i$ via the transition rules given in Table 1.
• Seeds. $p\left(1\right)=1$, $q\left(1\right)=l$, $\lambda \left(1\right)=\rho \left(1\right)=1$, and $s_0^i=1$ ($1\le i\le l$).
• Steps $1\le \nu \le n-2$. For $1\le i,k\le l$:

  $$\begin{array}{ccc}\hfill {\omega }_{\nu }^0,{\omega }_{\lambda \left(\nu \right)}^{p\left(\nu \right)}& ⟶\text{Equations (28),(29),(30)}⟶& {\alpha }_{\nu }^i,p(\nu +1),\lambda (\nu +1)\hfill \\ \hfill {\omega }_{\rho \left(\nu \right)}^{q\left(\nu \right)},{\omega }_{\nu }^{l+1}& ⟶\text{Equations (28),(29),(30)}⟶& {\beta }_{\nu }^i,q(\nu +1),\rho (\nu +1)\hfill \\ \hfill s_0^k,s_1^k,...,s_{\nu -1}^k,{\alpha }_{\nu }^i,{\beta }_{\nu }^i& ⟶\text{Equation (32)}⟶& s_{\nu }^i,s_{\nu }\hfill \end{array}$$
• Final step $\nu =n-1$. For $1\le i,k\le l$:

  $$\begin{array}{ccc}\hfill {\omega }_{n-1}^0,{\omega }_{\lambda (n-1)}^{p(n-1)}& ⟶\text{Equation (28)}⟶& {\alpha }_{n-1}^i\hfill \\ \hfill {\omega }_{\rho (n-1)}^{q(n-1)},{\omega }_{n-1}^{l+1}& ⟶\text{Equation (28)}⟶& {\beta }_{n-1}^i\hfill \\ \hfill s_0^k,s_1^k,...,s_{n-2}^k,{\alpha }_{n-1}^i,{\beta }_{n-1}^i& ⟶\text{Equation (32)}⟶& s_{n-1}^i,s_{n-1}\hfill \\ \hfill s_{1,}{s}_2,...,s_{n-1}& ⟶\text{Equation (31)}⟶& {\ell }_n\hfill \end{array}$$

From a computational point of view, the core of the calculation program is a loop that is exited when a chosen precision $\epsilon ={10}^{-d}$ in the estimation of $h\left(f\right)$ has been reached, i.e., when

$$\left|\frac{1}{\nu }log{\ell }_{\nu }-\frac{1}{\nu -1}log{\ell }_{\nu -1}\right|\le \epsilon$$

(otherwise, the loop is left with a flag after exceeding a preset maximal number of iterations $n_{max}$). In other words, the final step n is dynamically determined by the number d of exact decimal digits in the estimation of $h\left(f\right)$ —unless $n=n_{max}$ before getting that precision.

8. Numerical Simulations

The algorithm of Section 7 was implemented with the software package MATHEMATICA for arbitrary l, and run on an Intel(R) Core(TM)2 Duo CPU. The logarithms were taken to base 2, so the values of $h\left(f\right)$ are given in bits per iteration. We summarize next some numerical results obtained with 2- and 3-modal maps. In all these simulations, $n_{max}=500$.

8.1. Simulations with Bimodal Maps

The workhorse in most of our numerical simulations with bimodal maps was the two-parametric family of cubic polynomials

$$f_{v_1,v_2}\left(x\right)=(v_1-v_2)(16x^3-24x^2+9x)+v_2$$

where $x\in [0,1]$. These maps have convenient properties for numerical simulations as they share the same fixed critical points,

$$c_1=1/4,c_2=3/4$$

the critical values are precisely the parameters,

$$f_{v_1,v_2}(1/4)=v_1,f_{v_1,v_2}(3/4)=v_2$$

and the values of f at the endpoints are explicitly given by the parameters as follows:

$$f_{v_1,v_2}\left(0\right)=v_2,f_{v_1,v_2}\left(1\right)=v_1$$

Therefore, if we choose $v_1,v_2\in [0,1]$ with $v_1>v_2$, we obtain bimodal maps with a positive shape. It is customary to call control parameter(s) the parameter(s) labeling the maps of a family.

Figure 3 (left) shows the graphs of the full range map $f_{1,0}$, together with $f_{0.9,0.1}$ and $f_{0.8,0.2}$. The convergence rate of ${\left({\ell }_n\right)}^{1/n}$ to $2^{h\left(f\right)}$ for these three maps when n increases is shown in Figure 3 (right). The precision obtained for $h\left(f_{v_1,v_2}\right)$ in this range of parameters and $n=200$, is the following:

$$\left|\frac{1}{200}{log}_2{\ell }_{200}-\frac{1}{199}{log}_2{\ell }_{199}\right|=\left\{\begin{array}{cc}0.0000942...& \text{for}{f}_{0.9,0.1}\\ 0.0002204...& \text{for}{f}_{0.8,0.2}\end{array}\right.$$

For $n=500$, the estimation of $h\left(f_{0.8,0.2}\right)$ has four exact decimal digits.

Figure 3. Left, graphs of the maps $f_{1,0},f_{0.9,0.1},f_{0.8,0.2}$. Right, the corresponding convergence plots of ${\left({\ell }_n\right)}^{1/n}$ to $2^{h\left(f\right)}$ as a function of n (top to bottom).

Figure 3. Left, graphs of the maps $f_{1,0},f_{0.9,0.1},f_{0.8,0.2}$. Right, the corresponding convergence plots of ${\left({\ell }_n\right)}^{1/n}$ to $2^{h\left(f\right)}$ as a function of n (top to bottom).

A typical benchmark for estimators of the topological entropy consists in determining the entropy as a function of the control parameter(s). Since $f_{v_1,v_2}$ depends on two control parameters, we have calculated that dependence both on one parameter (while keeping fixed the other one), and on the two of them. Figure 4 is a plot of $h\left(f_{1,v_2}\right)$ vs. $v_2$. As $h\left(f_{1,v_2}\right)$ gets smaller, the number of iterations needed to get the entropy with a given precision grows higher. In Figure 4, the mesh constant used was $\Delta v_2={10}^{-3}$, and the precision $\epsilon ={10}^{-4}$.

Figure 5 is the same kind of plot, this time for $h\left(f_{v_1,v_2}\right)$ as a function of both control parameters, with $0.5\le v_1\le 1$, and $0\le v_2\le v_1-0.5$. This figure depicts also some level sets, just to illustrate the monotonicity of the topological entropy in the parametric space. This property, first conjectured by Milnor and Thurston [17], was later proved for quadratic maps in [18,19]. Only recently did H. Bruin and S. van Strien succeed in proving it also for multimodal maps [20]. The computation parameters were set as follows: $\Delta v_1=\Delta v_2=\epsilon ={10}^{-2}$.

Figure 4. Plot of $h\left(f_{1,v_2}\right)$ vs. $v_2$, $0\le v_2\le 1$.

Figure 4. Plot of $h\left(f_{1,v_2}\right)$ vs. $v_2$, $0\le v_2\le 1$.

Figure 5. Level sets of the plot of $h\left(f_{v_1,v_2}\right)$ vs. $v_1,v_2$, $0\le v_2\le v_1-0.5$.

Figure 5. Level sets of the plot of $h\left(f_{v_1,v_2}\right)$ vs. $v_1,v_2$, $0\le v_2\le v_1-0.5$.

8.2. Simulations with 3-Modal Maps

Consider next the 3-modal maps $f_{v_2,v_3}:[0,1]\to [0,1]$ defined by the quartic polynomials

$$\begin{array}{ccc}\hfill f_{v_2,v_3}\left(x\right)& =& \frac{4\left[\left(2\sqrt{2}-1\right)v_2-2v_3\right]x}{2(2\sqrt{2}+1)v_3-7v_2}\left[4\left(1+2\sqrt{2}\right)(x-1){(1-2x)}^2{v}_3\right.\hfill \\ & & +\left.\left(-56x^3+20\left(4+\sqrt{2}\right)x^2-\left(37+18\sqrt{2}\right)x+3\sqrt{2}+5\right)v_2\right]\hfill \end{array}$$

where $0\le v_2<v_3\le 1$. The derivative is

$$f_{v_2,v_3}^{\prime }\left(x\right)=A(x-c_1)(x-c_2)(x-c_3)$$

where $A=128\left(2\sqrt{2}{v}_2-v_2-2v_3\right)$, and

$$c_1=\frac{-\sqrt{2}{v}_2-4v_2+12\sqrt{2}{v}_3-8v_3}{8\left(-7v_2+4\sqrt{2}{v}_3+2v_3\right)},c_2=1/2,c_3=\frac{1}{4}(2+\sqrt{2})$$

This family verifies $f_{v_2,v_3}\left(0\right)=0$, $f_{v_2,v_3}\left(c_2\right)=v_2$, $f\left(c_3\right)=v_3$, and

$$f_{v_2,v_3}\left(1\right)=\frac{4\left(5\sqrt{2}-8\right)v_2\left(\left(2\sqrt{2}-1\right)v_2-2v_3\right)}{-7v_2+4\sqrt{2}{v}_3+2v_3}$$

Thus, $f_{v_2,v_3}$ has two fixed critical points ($c_2$ and $c_3$), while the critical point $c_1$ depends on the control parameters $v_2$, $v_3$. And again, $v_2$, $v_3$ coincide with the critical values at $c_2$ and $c_3$, respectively. The restriction $v_2<v_3$ postulated above relates to $v_2$ being a local minimum and $v_3$ a local maximum. Moreover, the left endpoint, $x=0$, is a fixed point.

In particular, the choice $v_2=0$ and $v_3=1$ produces a full range quartic, Figure 6, with equation

$$f_{0,1}\left(x\right)=-16x(x-1){(1-2x)}^2$$

Figure 7 (left) shows the dependence of $h\left(f_{v_2,1}\right)$ on the control parameter $0\le v_2<1$, while Figure 7 (right) does the same for $h\left(f_{0,v_3}\right)$ with $0<v_3\le 1$. As in the previous computation with a uniparametric cubic, $\Delta v_1=\Delta v_2={10}^{-3}$, and $\epsilon ={10}^{-4}$. Finally, Figure 8 depicts some level sets of $h\left(f_{v_2,v_3}\right)$ with $0\le v_2\le 5$ and $v_2+0.3\le v_3\le 1$. Here $\Delta v_1=\Delta v_2=\epsilon ={10}^{-2}$.

Figure 6. The full range quartic $f_{0,1}$.

Figure 6. The full range quartic $f_{0,1}$.

Figure 7. Left, plot of $h\left(f_{v_2,1}\right)$ vs. $v_2$, $0\le v_2<1$. Right, plot of $h\left(f_{0,v_3}\right)$ vs. $v_3$, $0<v_3\le 1$.

Figure 7. Left, plot of $h\left(f_{v_2,1}\right)$ vs. $v_2$, $0\le v_2<1$. Right, plot of $h\left(f_{0,v_3}\right)$ vs. $v_3$, $0<v_3\le 1$.

Figure 8. Level sets of the plot of $h\left(f_{v_2,v_3}\right)$ vs. $v_2,v_3$, $v_2+0.3\le v_3\le 1$.

Figure 8. Level sets of the plot of $h\left(f_{v_2,v_3}\right)$ vs. $v_2,v_3$, $v_2+0.3\le v_3\le 1$.

9. Conclusions

We have given an algorithm to efficiently calculate the lap number ${\ell }_n$ (hence, the topological entropy) for the iterates of a twice differentiable l-modal map f. The algorithm is based on $l+1$ symbolic sequences ${\left({\omega }_{\nu }^i\right)}_{\nu \in \mathbb{N}}$, $0\le i\le l+1$, —the min-max sequences of f—that contains qualitative information about the structure of maxima and minima of the map iterates $f^n$ and the orbits of the endpoints. Theorem 6.3 shows that ${\ell }_n$ is determined by the initial segments ${\left({\omega }_n^i\right)}_{1\le \nu \le n-1}$, hence by the itineraries of the critical and boundary points up to order $n-1$. This approach builds on previous results for unimodal, boundary-anchored maps obtained in [13] and [15] (Corollary 6.4) and [16]. To test if the topological entropy is positive, we test if the kneading sequences are similar or differ from the kneading sequences associated with the Feigenbaum period doubling cascade ([16], Section 5). If the kneading sequences are similar, than the map has zero topological entropy. Finally, we would like to add that the counting techniques developed here can be extended to maps with jump discontinuities and to piecewise continuous and monotonous maps. However in this case, the kneading sequence calculus must be substantially changed.