Compensated Transfer Entropy as a Tool for Reliably Estimating Information Transfer in Physiological Time Series
Abstract
:1. Introduction
2. Methods
2.1. Transfer Entropy
2.2. Compensated Transfer Entropy
2.3. Estimation Approach
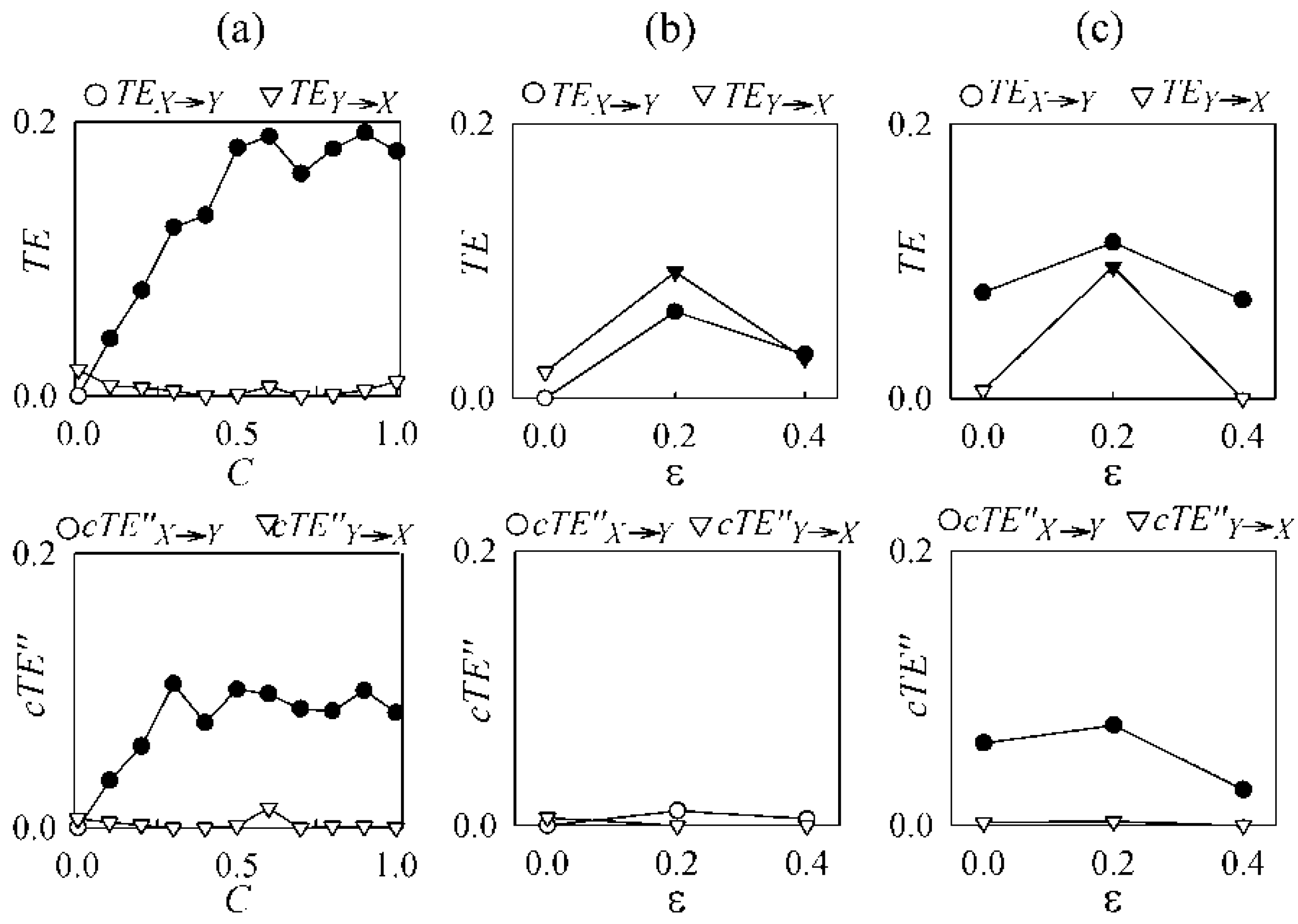
3. Validation
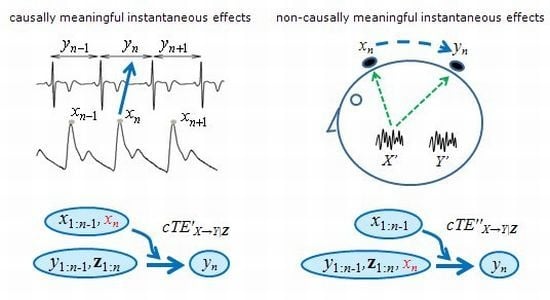
3.1. Physiologically Meaningful Instantaneous Causality
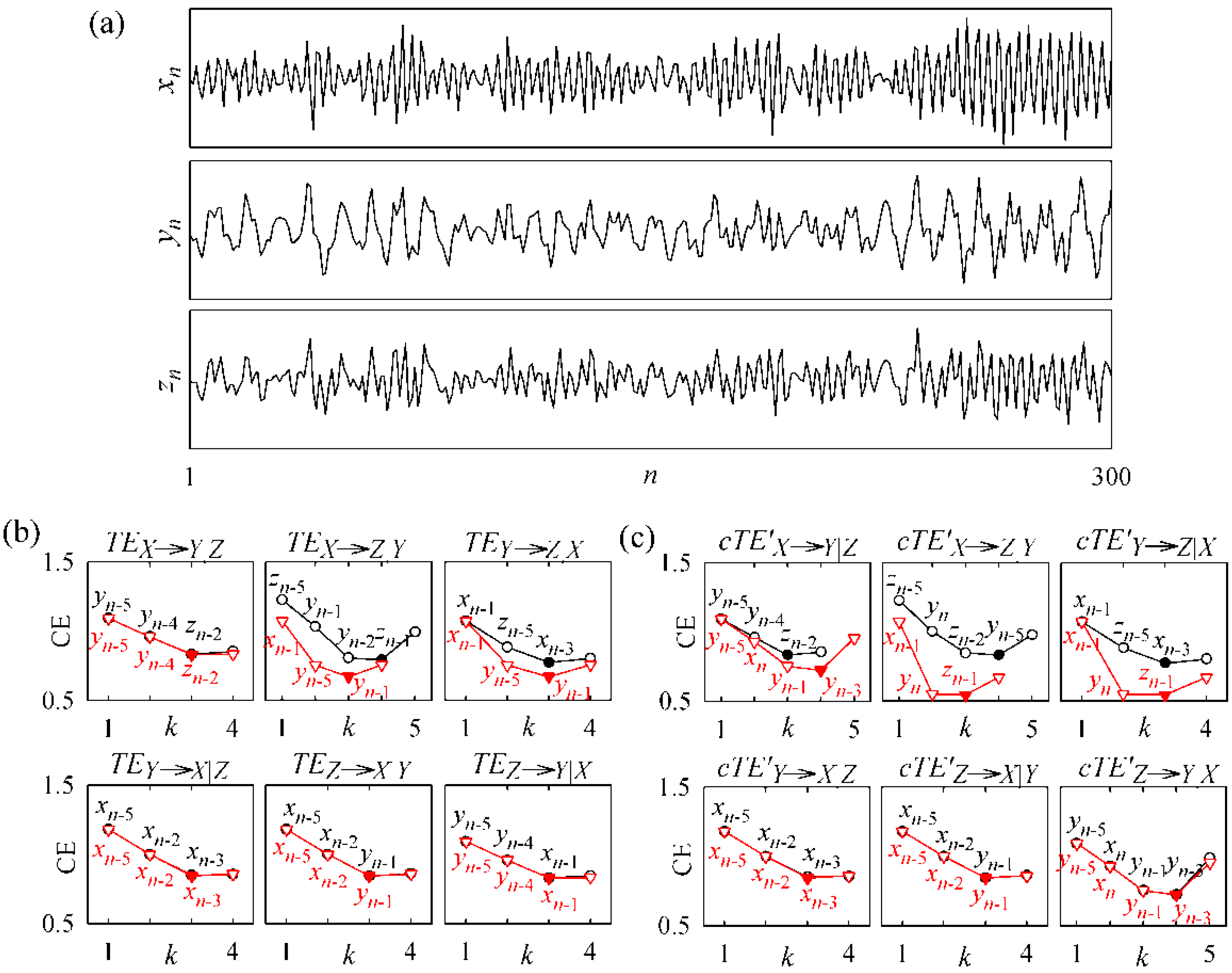
3.2. Non-Physiological Instantaneous Causality

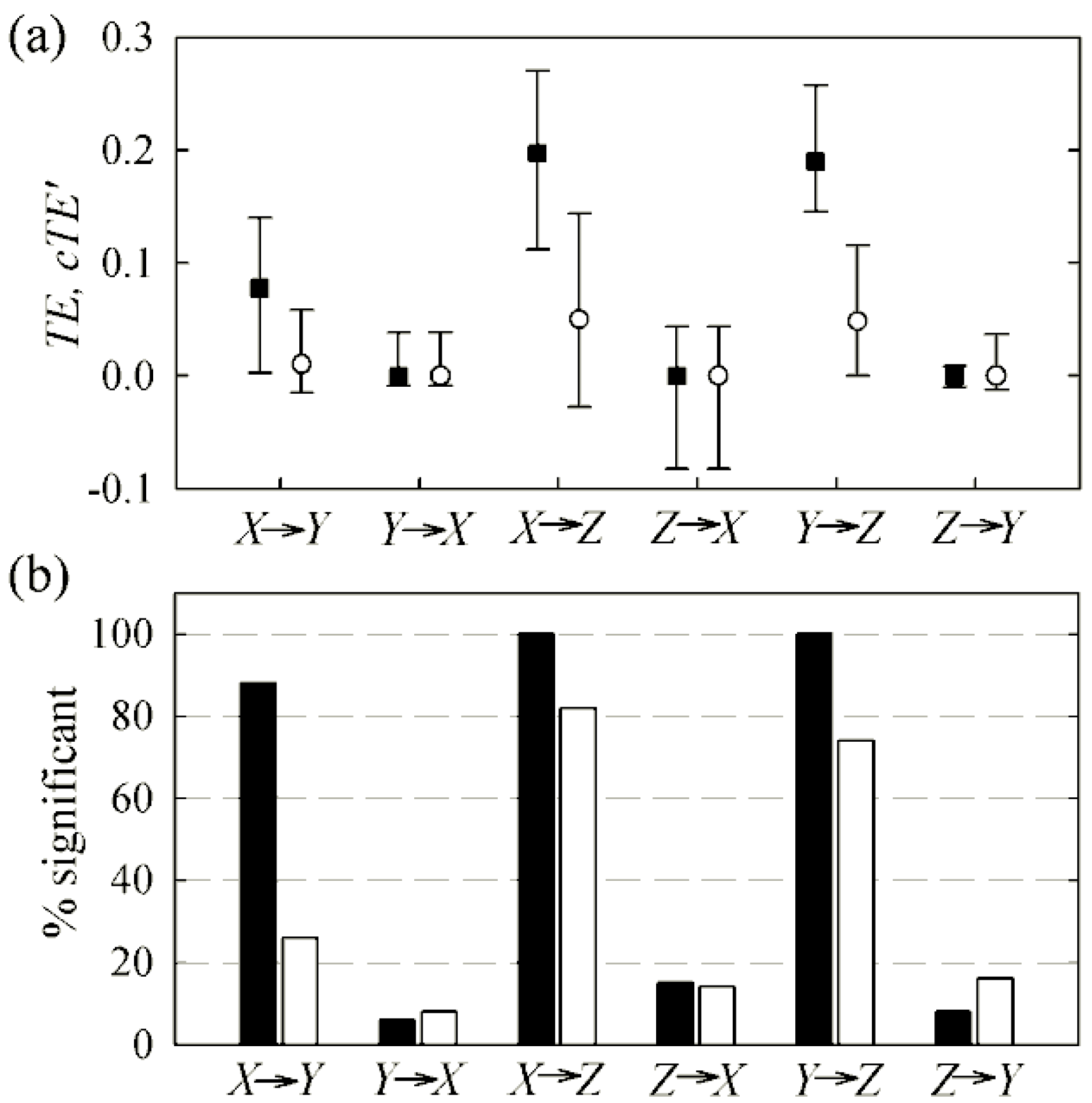
4. Application Examples
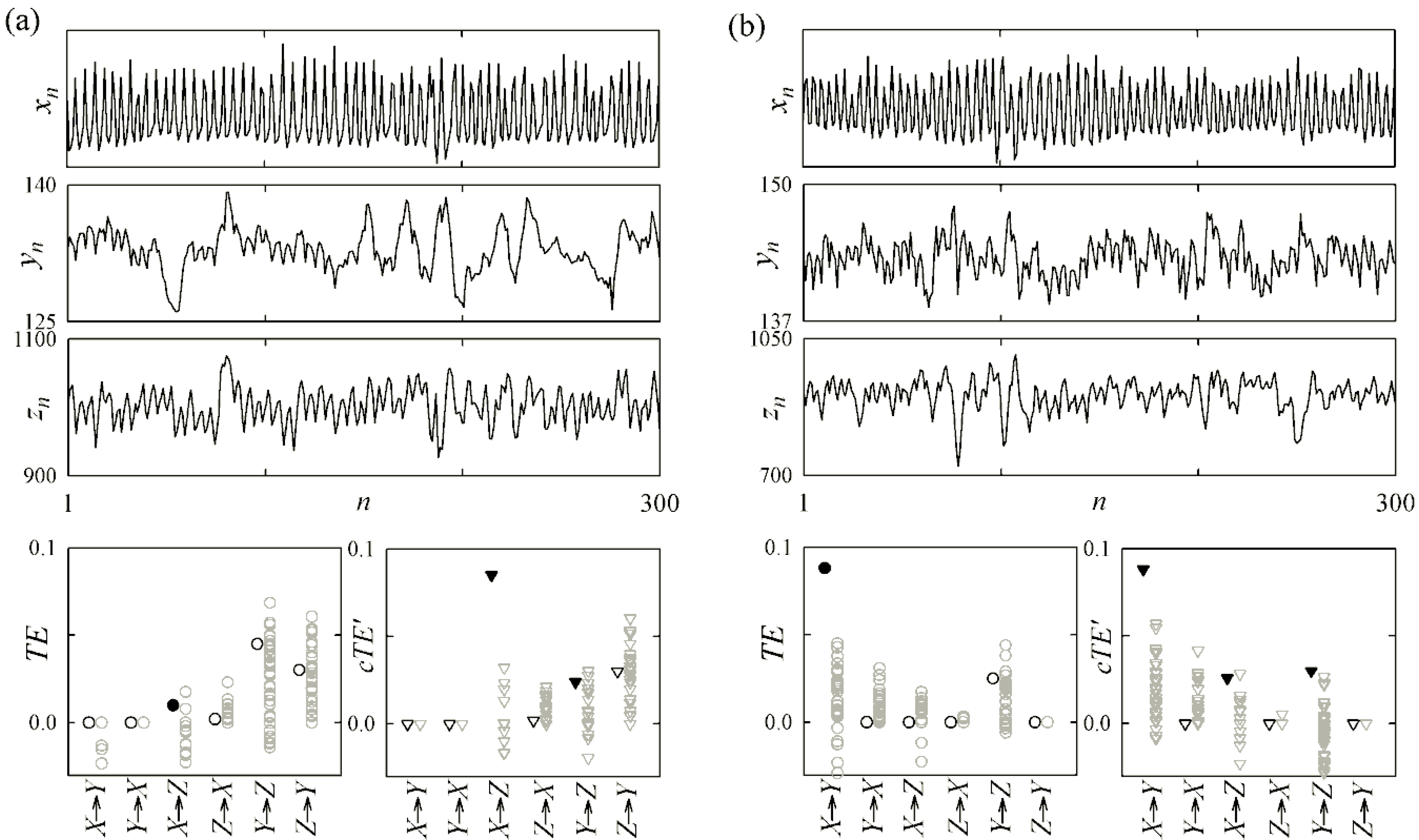
4.1. Cardiovascular and Cardiorespiratory Variability
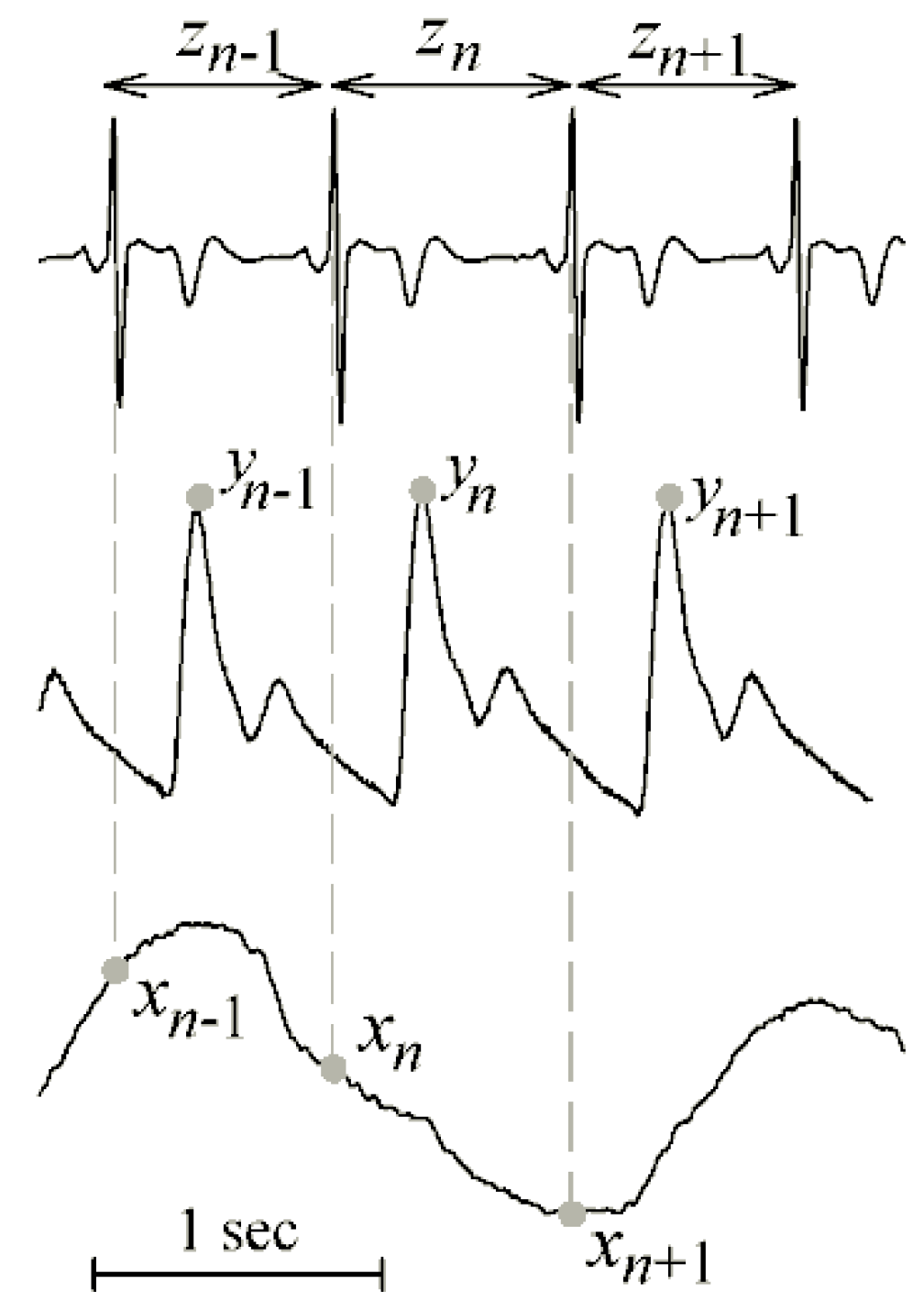
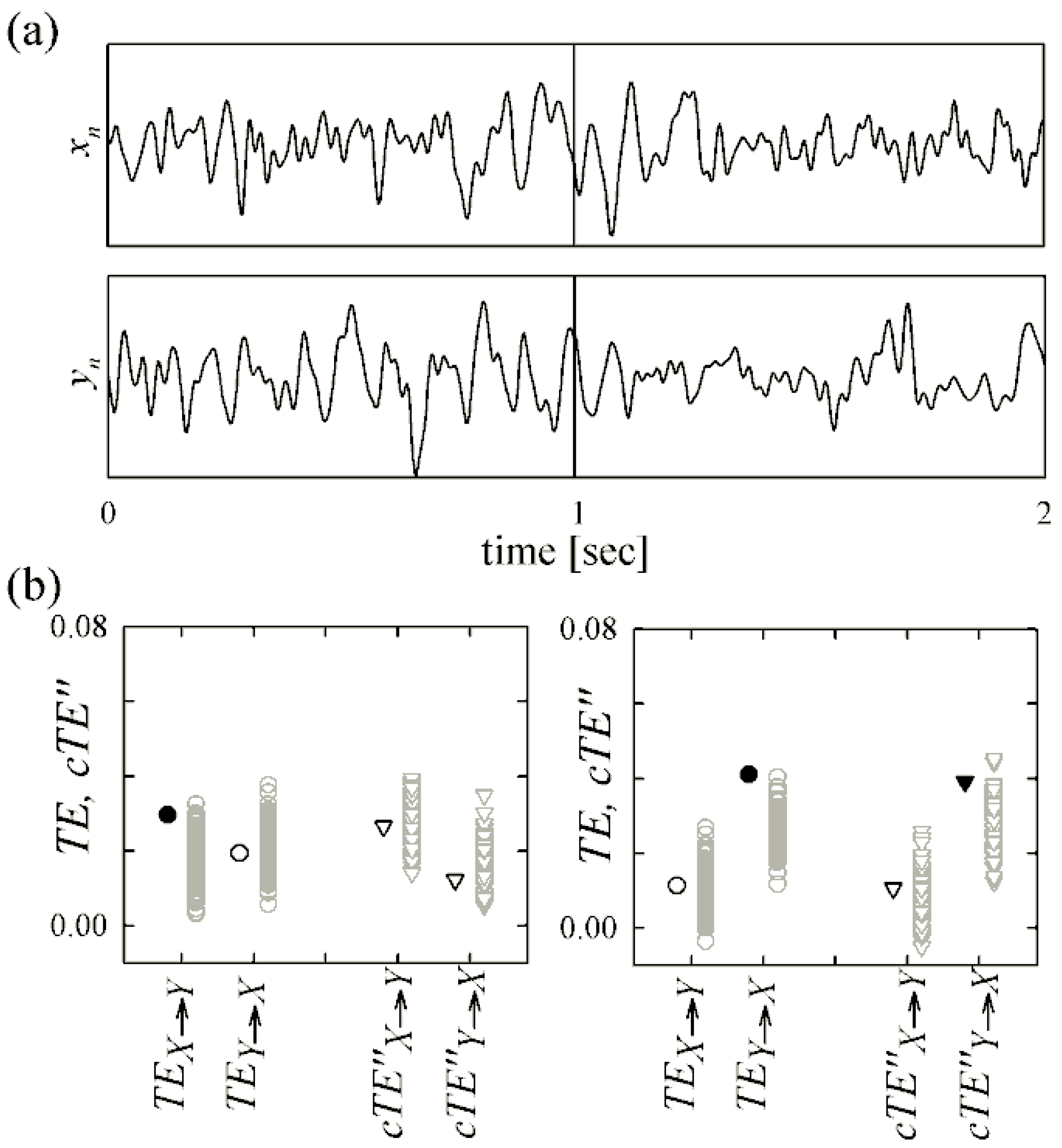
4.2. Magnetoencephalography
5. Discussion
References
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 2000, 461–464. [Google Scholar] [CrossRef]
- Barnett, L.; Barrett, A.B.; Seth, A.K. Granger causality and transfer entropy are equivalent for Gaussian variables. Phys. Rev. Lett. 2009, 103, 238701. [Google Scholar] [CrossRef] [PubMed]
- Wibral, M.; Rahm, B.; Rieder, M.; Lindner, M.; Vicente, R.; Kaiser, J. Transfer entropy in magnetoencephalographic data: Quantifying information flow in cortical and cerebellar networks. Progr. Biophys. Mol. Biol. 2011, 105, 80–97. [Google Scholar] [CrossRef] [PubMed]
- Vicente, R.; Wibral, M.; Lindner, M.; Pipa, G. Transfer entropy-a model-free measure of effective connectivity for the neurosciences. J. Comp. Neurosci. 2011, 30, 45–67. [Google Scholar] [CrossRef] [PubMed]
- Vakorin, V.A.; Kovacevic, N.; McIntosh, A.R. Exploring transient transfer entropy based on a group-wise ICA decomposition of EEG data. Neuroimage 2010, 49, 1593–1600. [Google Scholar] [CrossRef] [PubMed]
- Gourevitch, B.; Eggermont, J.J. Evaluating information transfer between auditory cortical neurons. J. Neurophysiol. 2007, 97, 2533–2543. [Google Scholar] [CrossRef] [PubMed]
- Faes, L.; Nollo, G.; Porta, A. Information domain approach to the investigation of cardio-vascular, cardio-pulmonary, and vasculo-pulmonary causal couplings. Front. Physiol. 2011, 2, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Faes, L.; Nollo, G.; Porta, A. Non-uniform multivariate embedding to assess the information transfer in cardiovascular and cardiorespiratory variability series. Comput. Biol. Med. 2012, 42, 290–297. [Google Scholar] [CrossRef] [PubMed]
- Vejmelka, M.; Palus, M. Inferring the directionality of coupling with conditional mutual information. Phys. Rev. E 2008, 77, 026214. [Google Scholar] [CrossRef]
- Chicharro, D.; Ledberg, A. Framework to study dynamic dependencies in networks of interacting processes. Phys. Rev. E 2012, 86, 041901. [Google Scholar] [CrossRef]
- Chicharro, D.; Ledberg, A. When two become one: The limits of causality analysis of brain dynamics. PLoS One 2012. [Google Scholar] [CrossRef] [PubMed]
- Lizier, J.T.; Prokopenko, M. Differentiating information transfer and causal effect. Eur. Phys. J. B 2010, 73, 605–615. [Google Scholar] [CrossRef]
- Hlavackova-Schindler, K.; Palus, M.; Vejmelka, M.; Bhattacharya, J. Causality detection based on information-theoretic approaches in time series analysis. Phys. Rep. 2007, 441, 1–46. [Google Scholar] [CrossRef]
- Lee, J.; Nemati, S.; Silva, I.; Edwards, B.A.; Butler, J.P.; Malhotra, A. Transfer Entropy Estimation and Directional Coupling Change Detection in Biomedical Time Series. Biomed. Eng. 2012. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Faes, L.; Nollo, G.; Porta, A. Information-based detection of nonlinear Granger causality in multivariate processes via a nonuniform embedding technique. Phys. Rev. E 2011, 83, 051112. [Google Scholar] [CrossRef]
- Lutkepohl, H. New Introduction to Multiple Time Series Analysis; Springer-Verlag: Heidelberg, Germany, 2005. [Google Scholar]
- Faes, L.; Erla, S.; Porta, A.; Nollo, G. A framework for assessing frequency domain causality in physiological time series with instantaneous effects. Philos. Transact. A 2013, in press. [Google Scholar] [CrossRef] [PubMed]
- Faes, L.; Nollo, G. Extended causal modelling to assess Partial Directed Coherence in multiple time series with significant instantaneous interactions. Biol. Cybern. 2010, 103, 387–400. [Google Scholar] [CrossRef] [PubMed]
- Granger, C.W.J. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Geweke, J. Measurement of linear dependence and feedback between multiple time series. J. Am. Stat. Assoc. 1982, 77, 304–313. [Google Scholar] [CrossRef]
- Guo, S.X.; Seth, A.K.; Kendrick, K.M.; Zhou, C.; Feng, J.F. Partial Granger causality—Eliminating exogenous inputs and latent variables. J. Neurosci. Methods 2008, 172, 79–93. [Google Scholar] [CrossRef] [PubMed]
- Barrett, A.B.; Barnett, L.; Seth, A.K. Multivariate Granger causality and generalized variance. Phys. Rev. E 2010, 81, 041907. [Google Scholar] [CrossRef]
- Hyvarinen, A.; Zhang, K.; Shimizu, S.; Hoyer, P.O. Estimation of a Structural Vector Autoregression Model Using Non-Gaussianity. J. Machine Learn. Res. 2010, 11, 1709–1731. [Google Scholar]
- Porta, A.; Bassani, T.; Bari, V.; Pinna, G.D.; Maestri, R.; Guzzetti, S. Accounting for Respiration is Necessary to Reliably Infer Granger Causality From Cardiovascular Variability Series. IEEE Trans. Biomed. Eng. 2012, 59, 832–841. [Google Scholar] [CrossRef] [PubMed]
- Vakorin, V.A.; Krakovska, O.A.; McIntosh, A.R. Confounding effects of indirect connections on causality estimation. J. Neurosci. Methods 2009, 184, 152–160. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Bressler, S.L.; Ding, M. Frequency decomposition of conditional Granger causality and application to multivariate neural field potential data. J. Neurosci. Methods 2006, 150, 228–237. [Google Scholar] [CrossRef] [PubMed]
- Kraskov, A.; Stogbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef]
- Porta, A.; Baselli, G.; Lombardi, F.; Montano, N.; Malliani, A.; Cerutti, S. Conditional entropy approach for the evaluation of the coupling strength. Biol. Cybern. 1999, 81, 119–129. [Google Scholar] [CrossRef] [PubMed]
- Takens, F. Detecting strange attractors in fluid turbulence. In Dynamical Systems and Turbulence; Rand, D., Young, S.L., Eds.; Springer-Verlag: Berlin, Germany, 1981; pp. 336–381. [Google Scholar]
- Vlachos, I.; Kugiumtzis, D. Nonuniform state-space reconstruction and coupling detection. Phys. Rev. E 2010, 82, 016207. [Google Scholar] [CrossRef]
- Small, M. Applied nonlinear time series analysis: Applications in physics, physiology and finance; World Scientific Publishing: Singapore, 2005. [Google Scholar]
- Runge, J.; Heitzig, J.; Petoukhov, V.; Kurths, J. Escaping the Curse of Dimensionality in Estimating Multivariate Transfer Entropy. Phys. Rev. Lett. 2012, 108, 258701. [Google Scholar] [CrossRef] [PubMed]
- Pincus, S.M. Approximate Entropy As A Measure of System-Complexity. Proc. Nat. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Porta, A.; Baselli, G.; Liberati, D.; Montano, N.; Cogliati, C.; Gnecchi-Ruscone, T.; Malliani, A.; Cerutti, S. Measuring regularity by means of a corrected conditional entropy in sympathetic outflow. Biol. Cybern. 1998, 78, 71–78. [Google Scholar] [CrossRef] [PubMed]
- Bollen, K.A. Structural equations with latent variables; John Wiley & Sons: NY, USA, 1989. [Google Scholar]
- Yu, G.H.; Huang, C.C. A distribution free plotting position. Stoch. Env. Res. Risk Ass. 2001, 15, 462–476. [Google Scholar] [CrossRef]
- Erla, S.; Faes, L.; Nollo, G.; Arfeller, C.; Braun, C.; Papadelis, C. Multivariate EEG spectral analysis elicits the functional link between motor and visual cortex during integrative sensorimotor tasks. Biomed. Signal Process. Contr. 2011, 7, 221–227. [Google Scholar] [CrossRef]
- Magagnin, V.; Bassani, T.; Bari, V.; Turiel, M.; Maestri, R.; Pinna, G.D.; Porta, A. Non-stationarities significantly distort short-term spectral, symbolic and entropy heart rate variability indices. Physiol Meas. 2011, 32, 1775–1786. [Google Scholar] [CrossRef] [PubMed]
- Cohen, M.A.; Taylor, J.A. Short-term cardiovascular oscillations in man: measuring and modelling the physiologies. J. Physiol 2002, 542, 669–683. [Google Scholar] [CrossRef] [PubMed]
- Hirsch, J.A.; Bishop, B. Respiratory sinus arrhythmia in humans: how breathing pattern modulates heart rate. Am. J. Physiol. 1981, 241, H620–H629. [Google Scholar] [PubMed]
- Toska, K.; Eriksen, M. Respiration-synchronous fluctuations in stroke volume, heart rate and arterial pressure in humans. J. Physiol 1993, 472, 501–512. [Google Scholar] [CrossRef] [PubMed]
- Erla, S.; Papadelis, C.; Faes, L.; Braun, C.; Nollo, G. Studying brain visuo-tactile integration through cross-spectral analysis of human MEG recordings. In Medicon 2010, IFMBE Proceedings; Bamidis, P.D., Pallikarakis, N., Eds.; Springer: Berlin, Germany, 2010; pp. 73–76. [Google Scholar]
- Marzetti, L.; del Gratta, C.; Nolte, G. Understanding brain connectivity from EEG data by identifying systems composed of interacting sources. Neuroimage 2008, 42, 87–98. [Google Scholar] [CrossRef] [PubMed]
- Bauer, M. Multisensory integration: A functional role for inter-area synchronization? Curr. Biol. 2008, 18, R709–R710. [Google Scholar] [CrossRef] [PubMed]
- Cole, S.R.; Platt, R.W.; Schisterman, E.F.; Chu, H.; Westreich, D.; Richardson, D.; Poole, C. Illustrating bias due to conditioning on a collider. Int. J. Epidemiol. 2010, 36, 417–420. [Google Scholar] [CrossRef] [PubMed]
- Marinazzo, D.; Pellicoro, M.; Stramaglia, S. Causal information approach to partial conditioning in multivariate data sets. Comput. Math. Methods Med. 2012, 2012, 303601. [Google Scholar] [CrossRef] [PubMed]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Faes, L.; Nollo, G.; Porta, A. Compensated Transfer Entropy as a Tool for Reliably Estimating Information Transfer in Physiological Time Series. Entropy 2013, 15, 198-219. https://doi.org/10.3390/e15010198
Faes L, Nollo G, Porta A. Compensated Transfer Entropy as a Tool for Reliably Estimating Information Transfer in Physiological Time Series. Entropy. 2013; 15(1):198-219. https://doi.org/10.3390/e15010198
Chicago/Turabian StyleFaes, Luca, Giandomenico Nollo, and Alberto Porta. 2013. "Compensated Transfer Entropy as a Tool for Reliably Estimating Information Transfer in Physiological Time Series" Entropy 15, no. 1: 198-219. https://doi.org/10.3390/e15010198