Expanding the Algorithmic Information Theory Frame for Applications to Earth Observation
Abstract
:1. Introduction
2. Preliminaries
3. Expanding the Frame
3.1. Pattern Recognition Based on Data Compression
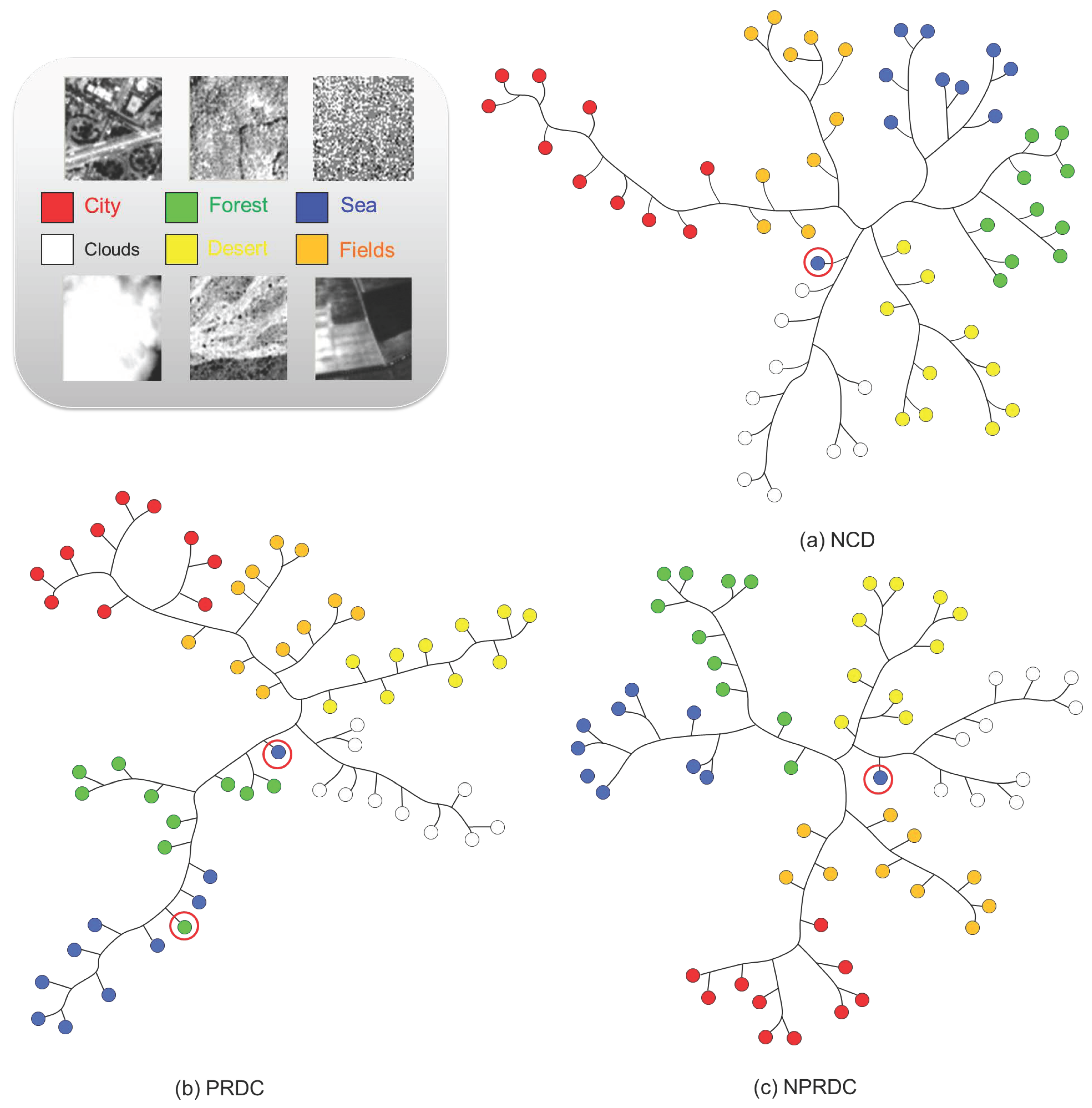
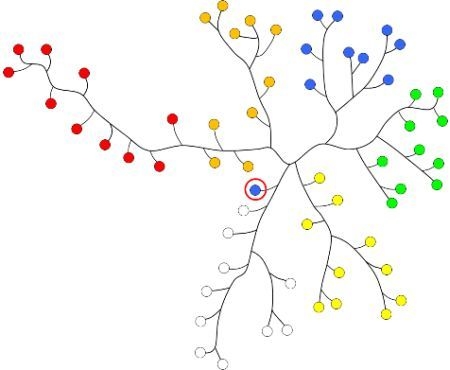
3.2. Relative Entropy
3.3. Delta Encoding as Conditional Compression
4. Conclusions
Acknowledgements
References
- Datcu, M.; Seidel, K.; Walessa, M. Spatial information retrieval from remote sensing images: Part A. information theoretical perspective. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1431–1445. [Google Scholar] [CrossRef]
- Cloude, S.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. Geosci. Remote Sens. IEEE Trans. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- Hegarat-Mascle, S.L.; Vidal-Madjar, D.; Taconet, O.; Zribi, M. Application of shannon information theory to a comparison between L- and C-band SIR-C polarimetric data versus incidence angle. Remote Sens. Environ. 1997, 60, 121–130. [Google Scholar] [CrossRef]
- Du, H.; Chang, C.; Ren, H.; Chang, C.; Jensen, J.; D’Amico, F. New hyperspectral discrimination measure for spectral characterization. Opt. Eng. 2004, 43, 1777–1786. [Google Scholar]
- Li, M.; Vitányi, P. An Introduction to Kolmogorov Complexity and Its Applications; Springer-Verlag: New York, NY, USA, 2008. [Google Scholar]
- Li, M.; Chen, X.; Li, X.; Ma, B.; Vitányi, P.M.B. The similarity metric. IEEE Trans. Inf. Theory 2004, 50, 3250–3264. [Google Scholar] [CrossRef]
- Keogh, E.; Lonardi, S.; Ratanamahatana, C. Towards Parameter-free Data Mining. In Proceedings of the tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Seattle, WA, USA, 22–25 August 2004; p. 215.
- Cerra, D.; Mallet, A.; Gueguen, L.; Datcu, M. Algorithmic information theory-based analysis of earth observation images: An assessment. IEEE Geosci. Remote Sens. Lett. 2010, 7, 8–12. [Google Scholar] [CrossRef]
- Quartulli, M.; Olaizola, I.G. A review of EO image information mining. ISPRS J. Photogr. Remote Sens. 2013, 75, 11–28. [Google Scholar] [CrossRef]
- Campana, B.J.L.; Keogh, E.J. A compression-based distance measure for texture. Stat. Anal. Data Min. 2010, 3, 381–398. [Google Scholar] [CrossRef]
- Cilibrasi, R.; Vitányi, P.M.B. Clustering by compression. IEEE Trans. Inf. Theory 2005, 51, 1523–1545. [Google Scholar] [CrossRef]
- Granados, A.; Cebrian, M.; Camacho, D.; Rodriguez, F. Evaluating the impact of information distortion on normalized compression distance. Coding Theory Appl. 2008, 5228, 69–79. [Google Scholar]
- Veganzones, M.A.; Datcu, M.; Graña, M. Dictionary based Hyperspectral Image Retrieval. In Proceedings of the1st International Conference on Pattern Recognition Applications and Methods, Vilamoura, Algarve, Portugal; 2012; pp. 426–432. [Google Scholar]
- Cerra, D.; Bieniarz, J.; Avbelj, J.; Reinartz, P.; Mueller, R. Compression-based unsupervised clustering of spectral signatures. In Proceedings of the Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), 2011 3rd Workshop on, Lisbon, Portugal, 6–9 June 2011; pp. 1–4.
- Cerra, D.; Datcu, M. Compression-based hierarchical clustering of SAR images. Remote Sens. Lett. 2010, 1, 141–147. [Google Scholar] [CrossRef]
- Cerra, D.; Datcu, M. Algorithmic relative complexity. Entropy 2011, 13, 902–914. [Google Scholar] [CrossRef]
- Watanabe, T.; Sugawara, K.; Sugihara, H. A new pattern representation scheme using data compression. IEEE Trans. Patt. Anal. Mach. Intell. 2002, 24, 579–590. [Google Scholar] [CrossRef]
- Nakajima, M.; Watanabe, T.; Koga, H. Compression-based Semantic-Sensitive Image Segmentation: PRDC-SSIS. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS’12), Munich, Germany, 22–27 July 2012.
- Ziv, J.; Lempel, A. Compression of individual sequences via variable-rate coding. IEEE Trans. Inf. Theory 1978, 24, 530–536. [Google Scholar] [CrossRef]
- Ziv, J.; Merhav, N. A measure of relative entropy between individual sequences with application to universal classification. IEEE Trans. Inf. Theory 1993, 39, 1270–1279. [Google Scholar] [CrossRef]
- Welch, T. Technique for high-performance data compression. Computer 1984, 17, 8–19. [Google Scholar] [CrossRef]
- Kaspar, F.; Schuster, H. Easily calculable measure for the complexity of spatiotemporal patterns. Phys. Rev. A 1987, 36, 842–848. [Google Scholar] [CrossRef] [PubMed]
- Soklakov, A. Occam’s razor as a formal basis for a physical theory. Found. Phys. Lett. 2002, 15, 107–135. [Google Scholar] [CrossRef]
- Solomonoff, R. The universal distribution and machine learning. Comput. J. 2003, 46, 598. [Google Scholar] [CrossRef]
- Sculley, D.; Brodley, C. Compression and Machine Learning: A New Perspective on Feature Space Vectors. In Proceedings of the Data Compression Conference, Snowbird, UT, USA, 28–30 March 2006; pp. 332–341.
- Cilibrasi, R.; Cruz, A.; de Rooij, S.; Keijzer, M. CompLearn. 2002. Available online: http://www.complearn.org (accessed on 20 November 2012).
- Benedetto, D.; Caglioti, E.; Loreto, V. Language trees and zipping. Phys. Rev. Lett. 2002, 88, 48702. [Google Scholar] [CrossRef]
- Goodman, J. Extended comment on language trees and zipping. 2002; arXiv:cond-mat/020238. [Google Scholar]
- Benedetto, D.; Caglioti, E.; Loreto, V. On J. Goodman’s comment to” Language Trees and Zipping”. 2002; arxiv: cond-mat/0203275. [Google Scholar]
- Puglisi, A.; Benedetto, D.; Caglioti, E.; Loreto, V.; Vulpiani, A. Data compression and learning in time sequences analysis. Phys. D 2003, 180, 92–107. [Google Scholar] [CrossRef]
- Shapira, D.; Storer, J. In place differential file compression. Comput. J. 2005, 48, 677. [Google Scholar] [CrossRef]
- Wyner, A.; Ziv, J.; Wyner, A. On the role of pattern matching in information theory. IEEE Trans. Inf. Theory 1998, 44, 2045–2056. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Cerra, D.; Datcu, M. Expanding the Algorithmic Information Theory Frame for Applications to Earth Observation. Entropy 2013, 15, 407-415. https://doi.org/10.3390/e15010407
Cerra D, Datcu M. Expanding the Algorithmic Information Theory Frame for Applications to Earth Observation. Entropy. 2013; 15(1):407-415. https://doi.org/10.3390/e15010407
Chicago/Turabian StyleCerra, Daniele, and Mihai Datcu. 2013. "Expanding the Algorithmic Information Theory Frame for Applications to Earth Observation" Entropy 15, no. 1: 407-415. https://doi.org/10.3390/e15010407