Law of Multiplicative Error and Its Generalization to the Correlated Observations Represented by the q-Product
Abstract
:1. Introduction
2. Additive Error and Multiplicative Error
3. Law of Error for Independent Observations
3.1. Additive Error
3.2. Multiplicative Error
4. Law of Error for Correlated Observations Represented by the q-Product
4.1. Additive Error
4.2. Multiplicative Error
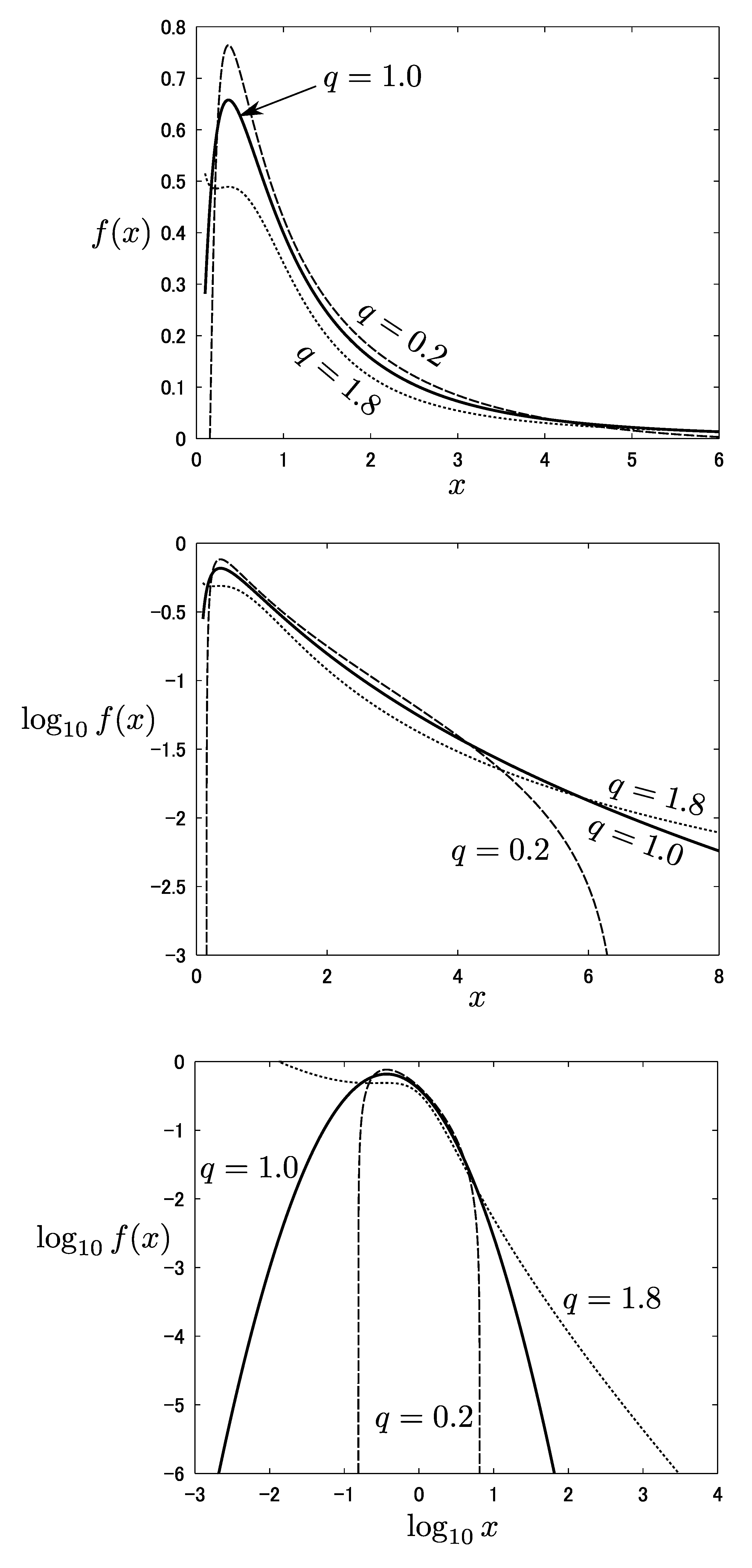
4.3. Reconsideration of Queirós’ q-Log-Normal Distribution in the Framework of the Law of Error
- independent observations, i.e., are i.i.d. random variables,
- The likelihood function of identical random variables is given by the -product of its pdf,
5. Conclusions
Acknowledgments
Conflict of Interest
Appendix: Proof of Theorem 13
References
- Tolman, R.C. The Principles of Statistical Mechanics; Dover: New York, NY, USA, 1938. [Google Scholar]
- Lavenda, B.H. Statistical Physics: A Probabilistic Approach; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Suyari, H. Mathematical structures derived from the q-multinomial coefficient in Tsallis statistics. Physica A 2006, 368, 63–82. [Google Scholar] [CrossRef]
- Gauss, C.F. Theoria Motus Corporum Coelestium in Sectionibus Conicis Solem Ambientium; Perthes: Hamburg, German, 1809; (translation with appendix by Davis, C.H. Theory of the Motion of the Heavenly Bodies Moving About the Sun in Conic Sections; Dover: New York, NY, 1963.). [Google Scholar]
- Hald, A. A History of Mathematical Statistics From 1750 to 1930; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Fisher, A.R. On the mathematical foundations of theoretical statistics. Philos. Trans. Roy. Soc. A, 1922, 222, 309–368. [Google Scholar] [CrossRef]
- Casella, G.; Berger, R.L. Statistical Inference, 2nd ed.; Cengage Learning: Stamford, CA, USA, 2001. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World; Springer: New York, NY, USA, 2009. [Google Scholar]
- Nivanen, L.; le Mehaute, A.; Wang, Q.A. Generalized algebra within a nonextensive statistics. Rep. Math. Phys. 2003, 52, 437–444. [Google Scholar] [CrossRef]
- Borges, E.P. A possible deformed algebra and calculus inspired in nonextensive thermostatistics. Physica A 2004, 340, 95–101. [Google Scholar] [CrossRef]
- Suyari, H.; Tsukada, M. Law of error in Tsallis statistics. IEEE Trans. Inform. Theory 2005, 51, 753–757. [Google Scholar] [CrossRef]
- Wada, T.; Suyari, H. κ-generalization of Gauss’ law of error. Phys. Lett. A 2006, 348, 89–93. [Google Scholar] [CrossRef]
- Scarfone, A.M.; Suyari, H.; Wada, T. Gauss’ law of error revisited in the framework of Sharma-Taneja-Mittal information measure. Centr. Eur. J. Phys. 2009, 7, 414–420. [Google Scholar] [CrossRef]
- Tsallis, C.; Levy, S.V.F.; Souza, A.M.C.; Maynard, R. Statistical-mechanical foundation of the ubiquity of Lévy distributions in nature. Phys. Rev. Lett. 1995, 75, 3589–3593. [Google Scholar] [CrossRef] [PubMed]
- Prato, D.; Tsallis, C. Nonextensive foundation of Levy distributions. Phys. Rev. E 1999, 60, 2398–2401. [Google Scholar] [CrossRef]
- Tsallis, C. What are the numbers that experiments provide? Quimica Nova 1994, 17, 468. [Google Scholar]
- Tsallis, C. What should a statistical mechanics satisfy to reflect nature? Physica D 2004, 193, 3–34. [Google Scholar] [CrossRef]
- Suyari, H.; Wada, T. Scaling Property and the Generalized Entropy Uniquely Determined by a Fundamental Nonlinear Differential Equation. In Proceedings of the 2006 International Symposium on Information Theory and its Applications, COEX, Seoul, Korea, 29 October 2006.
- Hilhorst, H.J.; Schehr, G. A note on q-Gaussians and non-Gaussians in statistical mechanics. J. Stat. Mech. 2007, P06003. [Google Scholar] [CrossRef]
- Dauxois, T. Non-Gaussian distributions under scrutiny. J. Stat. Mech. 2007, N08001. [Google Scholar] [CrossRef]
- Tsallis, C.; Mendes, R.S.; Plastino, A.R. The role of constraints within generalized nonextensive statistics. Physica A 1998, 261, 534–554. [Google Scholar] [CrossRef]
- Tsallis, C. What should a statistical mechanics satisfy to reflect nature? Physica D 2004, 193, 3–34. [Google Scholar] [CrossRef]
- Naudts, J. Generalised Thermostatistics; Springer: London, UK, 2011. [Google Scholar]
- Queirós, S.M.D. Generalised cascades. Braz. J. Phys. 2009, 39, 448–452. [Google Scholar] [CrossRef]
- Queirós, S.M.D. On generalisations of the log-Normal distribution by means of a new product definition in the Kaypten process. Physica A 2012, 391, 3594–3606. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Suyari, H. Law of Multiplicative Error and Its Generalization to the Correlated Observations Represented by the q-Product. Entropy 2013, 15, 4634-4647. https://doi.org/10.3390/e15114634
Suyari H. Law of Multiplicative Error and Its Generalization to the Correlated Observations Represented by the q-Product. Entropy. 2013; 15(11):4634-4647. https://doi.org/10.3390/e15114634
Chicago/Turabian StyleSuyari, Hiroki. 2013. "Law of Multiplicative Error and Its Generalization to the Correlated Observations Represented by the q-Product" Entropy 15, no. 11: 4634-4647. https://doi.org/10.3390/e15114634



