Statistical Mechanics Ideas and Techniques Applied to Selected Problems in Ecology
Abstract
:1. Introduction

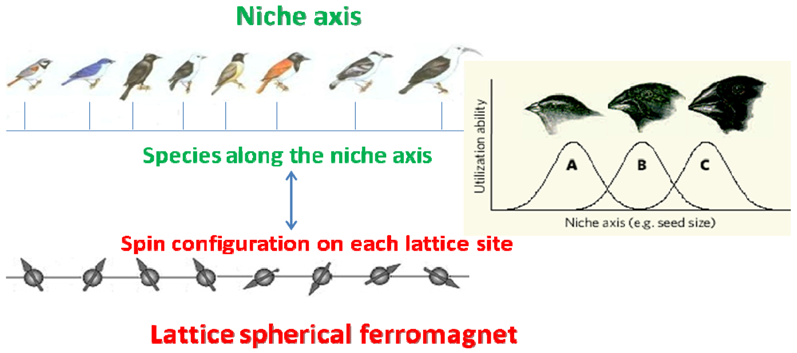
2. Mean Field Competition between Many Species along a Niche Axis: Emergent Neutrality
2.1. The Lotka-Volterra Competition Model and the MacArthur-Levins Niche Overlap Formula
2.2. An Analytical Proof of Self-Organized Similarity in a Simplified Case
- S1. The n species are evenly distributed along a finite niche axis of length L = 1, i.e., their mean sizes are given by μi = (i − 1)/n (i = 1, ..., n).
- S2. To avoid border effects, the niche is defined as circular, i.e., periodic boundary conditions (PBC) are imposed. This is done by just taking the smallest of |μi − μj| and 1 − |μi − μj| as the distance between the niche centers.
- S3. All species have the same niche width: σi = σ ∀i.
- S4. All species have the same per capita growth rate which we take equal to 1: ri = 1 ∀i.
- S5. All species have the same carrying capacity: Ki = K ∀i.



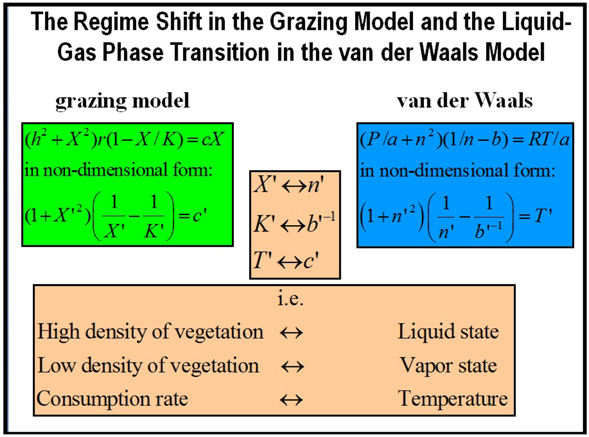
3. The Parallelism between a Spatial Grazing Model and Liquid-Gas Phase Transition: Metastability, Catastrophic Shifts in Ecosystems and Early Warnings [38]
3.1. Catastrophic Shifts beyond Mean Field Theory
- (i)
- How spatial heterogeneity of the environment and diffusion of matter and organisms affects the existence of alternative stable states.
- (ii)
- Whether emergent characteristic spatial patterns are really useful as early warnings and how they are connected with temporal signs of catastrophic shifts.
- (iii)
- The search for scaling laws underlying spatial patterns and self-organization.
3.2. The Mean Field Ecological Model


3.3. Spatial Model
- The spatial mean <X(t)>:
- The spatial variance σ2X:
- The temporal variance σ2t, computed from mean values of X at different times, which is defined as:for temporal bins of size τ (typical values for τ are from 50 to 150).
- The patchiness or cluster structure. Clusters of high (low) X are defined as connected regions of cells with X(i, j, t) > Xm (X(i, j, t) < Xm) where Xm is a threshold value. There are different criteria for defining Xm (see below).
- The two-point correlation function for pairs of cells at (i1, j1) and (i2, j2), separated by a given distance R, which is given by:G2(R) = <X(i1, j1)X(i2, j2)> − <X(i1, j1)><X(i2, j2)>
3.4. Alternative Stable States and Early Warnings
- Mean and Variances


- Correlation Function

- Patchiness: Cluster Structure

3.5. Usefulness of the Spatial Early Warnings


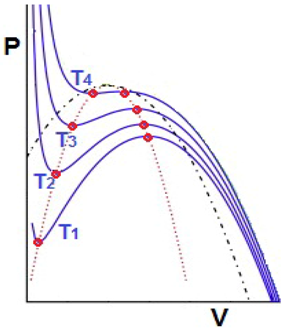
3.6. Comparison with the Boiling Phase Transition: From the Delay to the Maxwell Convention
- Modality: the fluid is bimodal within the coexistence region, having well defined liquid and gas states. Hence in this aspect both systems are similar.
- Sudden jumps: in the case of the fluid it is certainly true that sudden jumps occur, since there is an abrupt increase in volume when a liquid transforms into vapor. However, this large change in volume occurs when a slight change in the temperature and pressure moves the fluid from one side of the coexistence curve to the other. Hence, the liquid-vapor coexistence curve can be identified with SM and the water changes of state obey in general the Maxwell convention. On the other hand, the shift in the ecological model considered always obeys the delay convention: the ecosystem remains in the higher attractor (higher values of X) until the bifurcation set is completely traversed. However as mentioned before that, when perturbations are big enough to allow the switching between equilibriums on different stability branches, the system may follow the Maxwell convention. Hence we will consider the effect of a sudden perturbation of the environment, represented here by a sharp decrease of the average carrying capacity <K> followed by a slow recovery. Figure 13 shows the evolution of the system for such a perturbation in <K>. Instead of remaining close to the initial attractor (upper branch of K = 7.5), the system rapidly falls to the lower branch of K = 6.0 (which corresponds to the minimum value of the potential V). Next it approaches slowly to the lower branch of K = 7.5 until it arrives at it for c ≅ 1.915. So one can conclude that this type of perturbation on the system produces a change of convention: from delay to Maxwell.Figure 13. The effect on <X> of a global perturbation on <K> which suddenly decreases from <K> = 7.5 to 6 and slowly recovers later. Thin lines represent “iso-K” curves for K = 7.5 and K = 6.0.Figure 13. The effect on <X> of a global perturbation on <K> which suddenly decreases from <K> = 7.5 to 6 and slowly recovers later. Thin lines represent “iso-K” curves for K = 7.5 and K = 6.0.
- Hysteresis: in everyday situations one does not observe hysteresis in the liquid-gas phase transition of water—the liquid usually boils at the same temperature as the vapor condenses at. In other words, water changes of state obey in general the Maxwell convention. Nevertheless, a careful experimentalist can obtain a hysteresis cycle by first raising the temperature and superheating the liquid, and after evaporation, cooling the gas below the condensation point. Indeed the coexistence curve is surrounded by two spinodal lines which determine the limits to superheating and supersaturation. These spinodal or fold lines can then be identified with SB.
- Anomalous variance: when a fluid condenses (boils) from its gas (liquid) to its liquid (gas) state, small droplets (bubbles) are formed. As a consequence, the variance of the volume may become large, which is similar to what happens for the ecosystem. This study illustrates well that the ultimate cause of the wide variations in patch size, giving rise to scale invariance, is spatial heterogeneity both in the initial conditions and the physical environment (i.e., in K).
4. Nonequilibrium Dynamics in Cellular Automata Model for the Dynamics of Tropical Forests
4.1. Three Main Theories for Biodiversity—Classical, Neutral and Maxent—and the Use of Statistical Mechanics Methods
4.2. Describing Tropical Forests by the Transient Regime of Spatial LVCNT
4.3. A Cellular Automaton Model Based on Lotka-Volterra Competition Niche Theory
4.3.1. Estimation of Parameters
| Forest | L | n | σ, m, T | Species richness, S | |
|---|---|---|---|---|---|
| Pasoh (Malaysia) | 580 | 823 | 0.085, 0.11, 0.5 | 0.842 | 823, 819, 811, 808 823, 821 ± 2, 815 ± 4, 808 ± 5 |
| Barro Colorado (Panamá) | 500 | 320 | 0.077, 0.10, 3.0 | 0.694 | 320, 318, 303, 299, 292, 283 320, 314 ± 4, 300 ± 5, 293 ± 6, 287 ± 7, 281 ± 7 |
4.4. Results and Discussion



| Genus | Species | <dbh> (cm) * | max dbh (cm) * | Empirical Abundance ** | Theor. Abundance | Niche position |
|---|---|---|---|---|---|---|
| Hybanthus | Prunifolius | 2.24 | 8.8 | 29,846 | 31,115 | 0.008 |
| Faramea | Occidentalis | 4.54 | 23.2 | 26,038 | 29,560 | 0.998 |
| Trichilia | Tuberculata | 5.49 | 65.3 | 11,344 | 13,711 | 0.995 |
| Desmopsis | Panamensis | 2.59 | 13.1 | 11,327 | 13,152 | 0.012 |
| Alseis | Blackiana | 5.64 | 91.1 | 7,754 | 8,013 | 0.993 |
| Mouriri | Myrtilloides | 2.17 | 5.0 | 6,540 | 7,758 | 0.013 |
| Garcinia | Intermedia | 5.68 | 41.5 | 4,602 | 4,707 | 0.988 |
| Hirtella | Triandra | 4.71 | 48.3 | 4,566 | 4,193 | 0.984 |
| Tetragastris | Panamensis | 4.64 | 75.9 | 4,493 | 3,744 | 0.981 |
| Psychotria | Horizontalis | 1.77 | 6.3 | 3,119 | 3,443 | 0.021 |

5. Concluding Remarks
Acknowledgment
Conflicts of Interest
References
- Nee, S. The neutral theory of biodiversity: Do the numbers add up? Funct. Ecol. 2005, 19, 173–176. [Google Scholar]
- Scheffer, M. Critical Transitions in Nature and Society; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Cody, M.L.; Diamond, J.M. (Eds.) Ecology and Evolution of Communities; Belknap Press: Cambridge, MA, USA, 1975; pp. 342–444.
- McKane, A.J.; Newman, T.J. Predator-prey cycles from resonant amplification of demographic stochasticity. Phys. Rev. Lett. 2005, 94, 218102. [Google Scholar]
- Butler, T.; Goldenfeld, N. Robust ecological pattern formation induced by demographic noise. Phys. Rev. E 2009, 80. [Google Scholar] [CrossRef]
- Chia, N.; Goldenfeld, N. Statistical mechanics of horizontal gene transfer in evolutionary ecology. J. Stat. Phys. 2011, 142, 1287–1301. [Google Scholar]
- Blythe, R.A.; McKane, A.J. Stochastic models of evolution in genetics, ecology and linguistics. J. Stat. Mech. 2007. [Google Scholar] [CrossRef]
- Vladar, H.P.; Barton, N.H. The contribution of statistical physics to evolutionary biology. Trends Ecol. Evol. 2011, 26, 424–432. [Google Scholar]
- Harte, J.; Zillio, T.; Conlisk, E.; Smith, A.B. Maximum entropy and the state-variable approach to macroecology. Ecology 2008, 89, 2700–2711. [Google Scholar]
- Dewar, R.C.; Porté, A. Statistical mechanics unifies different ecological patterns. J. Theor. Biol. 2008, 251, 389–403. [Google Scholar]
- Volkov, I.; Banavar, J.; Hubbell, S.P.; Maritan, A. Neutral theory and relative species abundance in ecology. Nature 2003, 424, 1035–1037. [Google Scholar]
- Volkov, I.; Banavar, J.; He, F.; Hubbell, S.P.; Maritan, A. Density dependence explains tree species abundance and diversity in tropical forests. Nature 2005, 438, 658–661. [Google Scholar] [CrossRef] [PubMed]
- Volkov, I.; Banavar, J.; Hubbell, S.P.; Maritan, A. Patterns of relative species abundance in rainforests and coral reef. Nature 2007, 450, 45–49. [Google Scholar] [CrossRef] [PubMed]
- Banavar, J.R.; Maritan, A.; Volkov, I. Applications of the principle of maximum entropy: From physics to ecology. J. Phys. Condens. Matter 2010, 22. [Google Scholar] [CrossRef] [PubMed]
- Houchmandzadeh, B. Neutral clustering in a simple experimental ecological community. Phys. Rev. Lett. 2008, 101, 078103. [Google Scholar]
- Maurer, B.A. Statistical mechanics of complex ecological aggregates. Ecol. Complex. 2005, 2, 71–85. [Google Scholar]
- Solé, R.V.; Montoya, M. Complexity and fragility in ecological networks. Proc. R. Soc. Lond. B 2001, 268, 2039–2045. [Google Scholar] [CrossRef] [PubMed]
- Montoya, J.M.; Pimm, S.L.; Sole, R.V. Ecological networks and their fragility. Nature 2006, 442, 259–264. [Google Scholar] [CrossRef] [PubMed]
- Bastolla, U.; Fortuna, M.A.; Pascual-García, A.; Ferrera, A.; Luque, B.; Bascompte, J. The architecture of mutualistic networks minimizes competition and increases biodiversity. Nature 2009, 458, 1018–1020. [Google Scholar] [CrossRef] [PubMed]
- Suweis, S.; Simini, F.; Banavar, J.R.; Maritan, A. Emergence of structural and dynamical properties of ecological mutualistic networks. Nature 2013, 500, 449–452. [Google Scholar] [CrossRef] [PubMed]
- May, R.M. Stability and Complexity in Model Ecosystems; Princeton University Press: Princeton, NJ, USA, 1974. [Google Scholar]
- Tilman, D.; Lehman, C.L.; Kareiva, P. Population Dynamics in Spatial Habitats. In Spatial Ecology: The Role of Space in Population Dynamics and Interspecific Interaction; Tilman, D., Kareiva, P.M., Eds.; Princeton University Press: Princeton, NJ, USA, 1997; pp. 3–20. [Google Scholar]
- Lomolino, M.; Brown, J.; Brown, T.E. Biogeography; Sinauer Associates: Sunderland, MA, USA, 1998. [Google Scholar]
- MacArthur, R.H.; Levins, R. The limiting similarity, convergence and divergence of coexisting species. Am. Nat. 1967, 101, 377–385. [Google Scholar]
- Scheffer, M.; van Nes, E. Self-organized similarity, the evolutionary emergence of groups of similar species. Proc. Natl. Acad. Sci. USA 2006, 103, 6230–6235. [Google Scholar]
- Nee, S.; Colegrave, N. Ecology: Paradox of the clumps. Nature 2006, 441, 417–418. [Google Scholar]
- May, R.M.; Crawley, J.M.; Sugihara, G. Theoretical Ecology Principles and Applications; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Siemann, E.; Brown, J.H. Gaps in mammalian body size distributions reexamined. Ecology 1999, 80, 2788–2792. [Google Scholar]
- Holling, C.S. Cross-scale morphology, geometry and dynamics of ecosystems. Ecol. Monogr. 1992, 62, 447–502. [Google Scholar]
- Segura, A.M.; Kruk, C.; Calliari, D.; García-Rodriguez, F.; Conde, D.; Widdicombe, C.E.; Fort, H. Competition drives clumpy species coexistence in estuarine phytoplankton. Sci. Rep. 2013. [Google Scholar] [CrossRef]
- Segura, A.M.; Calliari, D.; Kruk, C.; Bonilla, S.; Conde, D.; Fort, H. Emergent neutrality drives phytoplankton species coexistence. Proc. R. Soc. B 2011, 278, 2355–2361. [Google Scholar]
- Fort, H.; Scheffer, M.; van Nes, E. The paradox of the clumps mathematically explained. Theor. Ecol. 2009, 2, 171–176. [Google Scholar]
- Fort, H.; Scheffer, M.; van Nes, E. The clumping transition in niche competition: A robust critical phenomenon. J. Stat. Mech. 2010, 2010. [Google Scholar] [CrossRef]
- Vergnon, R.; van Nes, E.H.; Scheffer, M. Emergent neutrality leads to multimodal species abundance distributions. Nat. Commun. 2012, 3. [Google Scholar] [CrossRef]
- Berlin, T.H.; Kac, M. The spherical model of a ferromagnet. Phys. Rev. 1952, 86, 821–835. [Google Scholar]
- Ziman, J.M. Models of Disorder: The Theoretical Physics of Homogeneously Disordered Systems; Cambridge University Press: Cambridge, UK, 1979; pp. 182–186. [Google Scholar]
- Gray, R.M. Toeplitz and Circulant Matrices: A Review; Now Publisher Inc.: Hanover, MA, USA, 2006; pp. 1–5. [Google Scholar]
- Fernández, A.; Fort, H. Catastrophic phase transitions and early warnings in a spatial ecological model. J. Stat. Mech. 2009, 2009. [Google Scholar] [CrossRef]
- Dregne, H.E. Desertification of Arid Lands. In Physics of Desertification; El-Baz, F., Hassan, M.H.A., Eds.; Martinus Nijhoff: Dordrecht, The Netherlands, 1986. [Google Scholar]
- Scheffer, M. Ecology of Shallow Lakes; Chapman and Hall: London, UK, 1998. [Google Scholar]
- Carpenter, S.R.; Ludwig, D.; Brock, W.A. Management of eutrophication for lakes subject to potentially irreversible change. Ecol. Appl. 1999, 9, 751–771. [Google Scholar]
- Scheffer, M.; Carpenter, S.; Foley, J.A.; Folke, C.; Walker, B. Catastrophic shifts in ecosystems. Nature 2001, 413, 591–596. [Google Scholar]
- Carpenter, S. Alternate States of Ecosystems: Evidence and Some Implications. In Ecology: Achievement and Challenge; Huntly, N., Press, M.C., Levin, S., Eds.; Blackwell: Oxford, UK, 2001; pp. 357–383. [Google Scholar]
- Steinberg, E.K.; Kareiva, P. Challenges and Opportunities for Empirical Evaluation of Spatial Theory. In Spatial Ecology: The Role of Space in Population Dynamics and Interspecific Interaction; Tilman, D., Kareiva Princeton, P., Eds.; Princeton University Press: Princeton, NJ, USA, 1997; pp. 318–332. [Google Scholar]
- Levin, S.A.; Pacala, S.W. Theories of Simplification and Scaling of Spatially Distributed Processes. In Spatial Ecology: The Role of Space in Population Dynamics and Interspecific Interaction; Tilman, D., Kareiva Princeton, P., Eds.; Princeton University Press: Princeton, NJ, USA, 1997; pp. 271–296. [Google Scholar]
- Aguiar, M.R.; Sala, O.E. Patch structure, dynamics and implications for the functioning of arid ecosystems. Tree 1999, 14, 273–277. [Google Scholar]
- Klausmeier, C.A. Regular and irregular patterns in semiarid vegetation. Science 1999, 284, 1826–1828. [Google Scholar]
- Von Hardenberg, J.; Meron, E.; Shachak, M.; Zarmi, Y. Diversity of vegetation patterns and desertification. Phys. Rev. Lett. 2001, 87, 1981011. [Google Scholar] [CrossRef]
- Von Hardenberg, J.; Kletter, A. Y.; Yizhaq, H.; Nathan, J.; Meron, E. Periodic versus scale-free patterns in dryland vegetation. Proc. R. Soc. B 2010, 277, 1771–1776. [Google Scholar] [CrossRef] [PubMed]
- Bel, G.; Hagberg, A.; Meron, E. Gradual regime shifts in spatially extended ecosystems. Theoretical Ecology 2012, 5, 591–604. [Google Scholar]
- Rietkerk, M.; Dekker, S.C.; de Ruiter, P.C.; van de Koppel, J. Self-organized patchiness and catastrophic shifts in ecosystems. Science 2004, 305, 1926–1928. [Google Scholar]
- Kéfi, S.; Rietkerk, M.; Alados, C.L.; Pueyo, Y.; Papanastasis, V.P.; ElAich, A.; de Ruiter, P.C. Spatial vegetation patterns and imminent desertification in Mediterranean arid ecosystems. Nature 2007, 449, 213–217. [Google Scholar]
- Carpenter, S.R.; Brock, W.A. Rising variance: A leading indicator of ecological transition. Ecol. Lett. 2006, 9, 311–318. [Google Scholar]
- Brock, W.A.; Carpenter, S.R. Variance as a leading indicator of regime shift in ecosystem services. Ecol. Soc. 2006, 11. Art. 9. [Google Scholar]
- Noy-Meir, I. Stability of grazing systems: An application of predator-prey graphs. J. Ecol. 1975, 63, 459–481. [Google Scholar]
- World Resources Institute. World Resources 1988–89; Basic Books: New York, NY, USA, 1988. [Google Scholar]
- Wade, N. Sahelian drought: No victory for western aid. Science 1974, 185, 234–237. [Google Scholar]
- May, R.M. Thresholds and breakpoints in ecosystems with a multiplicity of stable states. Nature 1977, 269, 471–477. [Google Scholar]
- Ludwig, D.; Jones, D.D.; Holling, C.S. Qualitative analysis of insect outbreak systems: The spruce budworm and forest. J. Anim. Ecol. 1978, 47, 315–322. [Google Scholar]
- Murray, J.D. Mathematical Biology; Springer: Berlin, Germany, 1993. [Google Scholar]
- Holling, C.S. The components of predation as revealed by a study of small mammal predation of the European pine sawfly. Can. Entomol. 1959, 91, 293–320. [Google Scholar]
- Thom, R. Structural Stability and Morphogenesis: An Outline of a General Theory of Models; Addison-Wesley: Boston, MA, USA, 1975. [Google Scholar]
- Gilmore, R. Catastrophe Theory for Scientists and Engineers; Dover: New York, NY, USA, 1981. [Google Scholar]
- Boettiger, C.; Ross, N.; Hastings, A. Early warning signals: The charted and uncharted territories. Theor. Ecol. 2013, 6, 255–264. [Google Scholar]
- Goldenfeld, N. Lecture on Phase Transitions and the Renormalization Group; Perseus Books: Reading, MA, USA, 1992; pp. 219–222. [Google Scholar]
- Monette, L.; Klein, W. Spinodal decomposition as a coalescence process. Phys. Rev. Lett. 1992, 68, 2336–2339. [Google Scholar]
- Preston, F.W. The commonness, and rarity, of species. Ecology 1948, 29, 254–283. [Google Scholar]
- Rosenzweig, M.L. Species Diversity in Space and Time; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Gaston, K.J.; Blackburn, T.M. Pattern and Process in Macroecology; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Brown, J.H. Macroecology; University of Chicago Press: Chicago, IL, USA, 1995. [Google Scholar]
- Harte, J.; Conlisk, E.; Ostling, A.; Green, J.L.; Smith, A.B. A theory of spatial-abundance and species-abundance distributions in ecological communities at multiple spatial scales. Ecol. Monogr. 2004, 75, 179–197. [Google Scholar]
- Begon, M.; Townsend, C.; Harper, J. Ecology: From Individuals to Ecosystems, 4th ed.; Blackwell: New York, NY, USA, 2006. [Google Scholar]
- Hutchinson, G.E. Concluding remarks. Cold Spring Harb. Symp. Quant. Biol. 1957, 22, 415–427. [Google Scholar]
- Hubbell, S.P. The Unified Neutral Theory of Biodiversity and Biogeography; Princeton University Press: Princeton, NJ, USA, 2001. [Google Scholar]
- Condit, R.; Hubbell, S.P.; Lafrankie, J.V.; Sukumar, R.; Manokaran, N.; Foster, R.B.; Ashton, P.S. Species-area and species-individual relationships for tropical trees: A comparison of three 50-ha plots. J. Ecol. 1996, 84, 549–562. [Google Scholar]
- Chave, J. Neutral theory and community ecology. Ecol. Lett. 2004, 7, 241–253. [Google Scholar]
- Harte, J. Maximum Entropy and Ecology: A Theory of Abundance, Distribution, and Energetics; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Harte, J.; Smith, A.; Storch, D. Biodiversity scales from plots to biomes with a universal species-area curve. Ecol. Lett. 2009, 12, 789–797. [Google Scholar] [CrossRef] [PubMed]
- Jaynes, E.T. Notes on Present Status and Future Prospects. In Maximum Entropy and Bayesian Methods; Grandy, W.T., Jr., Schick, L.H., Eds.; Springer: Dordrecht, The Netherlands, 1991; Volume 43, pp. 1–13. [Google Scholar]
- McKane, A.J.; Alonso, D.; Sole, R.V. Analytic solution of Hubbell’s model of local community dynamics. Theor. Popul. Biol. 2004, 65, 67–73. [Google Scholar]
- Zillio, T.; Volkov, I.; Banavar, J.; Hubbell, S.P.; Maritan, A. Spatial scaling in model plant communities. Phys. Rev. E 2005, 71, 1507–1519. [Google Scholar] [CrossRef]
- Chave, J.; Leigh, E.G., Jr. A spatially explicit neutral model of beta-diversity in tropical forests. Theor. Popul. Biol. 2002, 62, 153–158. [Google Scholar] [CrossRef] [PubMed]
- Rosindell, J.; Cornell, S.J. Species-area relationships from a spatially explicit neutral model in an infinite landscape. Ecol. Lett. 2007, 10, 586–595. [Google Scholar] [CrossRef] [PubMed]
- Etienne, R.S.; Alonso, D. Neutral community theory: How stochasticity and and dispersal-limitation can explain species coexistence. J. Stat. Phys. 2007, 128, 485–510. [Google Scholar] [CrossRef]
- Bertuzzo, E.; Suweis, S.; Mari, L.; Maritan, A.; Rodríguez-Iturbe, I.; Rinaldo, A. Spatial effects on species persistence and implications for biodiversity. Proc. Natl. Acad. Sci. USA 2011, 108, 4346–4351. [Google Scholar] [CrossRef] [PubMed]
- Goel, N.S.; Maitra, S.C.; Montroll, E.W. On the volterra and other nonlinear models of intereacting populations. Rev. Mod. Phys. 1971, 43, 231–276. [Google Scholar] [CrossRef]
- Maynard Smith, J. Models in Ecology; Cambridge University Press: Cambridge, UK, 1974; pp. 90–97. [Google Scholar]
- Wilson, A. Boltzmann, Lotka and Volterra and spatial structural evolution: An integrated methodology for some dynamical systems. J. R. Soc. Interface 2008, 5, 865–871. [Google Scholar] [CrossRef] [PubMed]
- Tainaka, K. Lattice model for the Lotka-Volterra system. J. Phys. Soc. Jpn. 1988, 57, 2588–2590. [Google Scholar] [CrossRef]
- Matsuda, H.; Ogita, N.; Sasaki, A.; Sato, K. Statistical mechanics of population: The lattice Lotka-Volterra model. Prog. Theor. Phys. 1992, 88, 1035–1049. [Google Scholar] [CrossRef]
- Wilson, W.G.; de Roos, A.M.; McCauley, E. Spatial instabilities whitin the diffusive Lotka-Volterra system: Individual-based simulation results. Theor. Popul. Biol. 1993, 43, 91–127. [Google Scholar] [CrossRef]
- Szabó, G.; Czárán, T. Phase transition in a spatial Lotka-Volterra model. Phys. Rev. E 2001, 63, 061904. [Google Scholar] [CrossRef]
- Leimar, O.; Sasaki, A.; Doebeli, M.; Dieckmann, U. Limiting similarity, species packing, and the shape of competition kernels. J. Theor. Biol. 2013, 339, 3–13. [Google Scholar] [CrossRef] [PubMed]
- Fort, H.; Inchausti, P. Biodiversity patterns from an individual-based competition model on niche and physical spaces. J. Stat. Mech. 2012, 2012. [Google Scholar] [CrossRef]
- Fort, H.; Inchausti, P. Tropical forests are non-equilibrium ecosystems governed by interspecific competition based on a universal 1/6 niche width. PLOS One 2013, in press. [Google Scholar] [CrossRef] [PubMed]
- Center for Tropical Forest Science. Available online: http://www.ctfs.si.edu/ (accessed on 25 November 2013).
- Azaele, S.; Pigolotti, S.; Banavar, J.; Maritan, A. Dynamical evolution of ecosystems. Nature 2006, 444, 926–928. [Google Scholar] [CrossRef] [PubMed]
- Vanpeteghem, D.; Haegeman, B. An analytical approach to spatio-temporal dynamics of neutral community models. J. Math. Biol. 2010, 61, 323–357. [Google Scholar] [CrossRef] [PubMed]
- Chisholm, R.A. Time-dependent solutions of the spatially implicit neutral model of biodiversity. Theor. Popul. Biol. 2011, 80, 71–79. [Google Scholar] [CrossRef] [PubMed]
- Suweis, S.; Rinaldo, A.; Maritan, A. An exactly solvable coarse-grained model for species diversity. J. Stat. Mech. 2012, 2012. [Google Scholar] [CrossRef]
- Carey, S.; Ostling, A.; Harte, J.; del Moral, R. Impact of curve construction and community dynamics on the species-time relationship. Ecology 2007, 88, 2145–2153. [Google Scholar] [CrossRef] [PubMed]
- Hubbell, S.P. Neutral theory and the evolution of ecological equivalence. Ecology 2006, 87, 1387–1398. [Google Scholar]
- Morin, R.J. Community Ecology, 2nd ed.; John Wiley & Sons: Chichester, West Sussex, UK, 2011; pp. 26–27. [Google Scholar]
- Dieckmann, U.; Law, R.; Metz, J.A. (Eds.) The Geometry of Ecological Interactions; Cambridge University Press: Cambridge, UK, 2000.
- Glauber, R.J. Time-dependent statistics of the ising model. J. Math. Phys. 1963, 4, 294–307. [Google Scholar]
- Krapivsky, P.J.; Redner, S.; Ben Naim, E. A Kinetic View of Statistical Physics; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Fort, H. A minimal model for the evolution of cooperation through evolving heterogeneous games. Europhys. Lett. 2008, 81. [Google Scholar] [CrossRef]
- Condit, R.; Ashton, P.S.; Manokaran, N.; LaFrankie, J.V.; Hubbell, S.P.; Foster, R.B. Dynamics of the forest communities at Pasoh and Barro Colorado: Comparing two 50-ha plots. Philos. Trans. R. Soc. B 1999, 354, 1739–1748. [Google Scholar]
- Hubbell, S.P.; Condit, R.; Foster, R.B. Forest Census Plot on Barro Colorado Island. Available online: http://ctfs.arnarb.harvard.edu/webatlas/datasets/bci (accessed on 25 November 2013).
- Condit, R. Tropical Forest Census Plots; Springer: New York, NY, USA, 1998. [Google Scholar]
- Hubbell, S.P.; Ahumada, J.A.; Condit, R.; Foster, R.B. Local neighborhood effects on long-term survival of individual trees in a neotropical forest. Ecological Research 2001, 16, 859–875. [Google Scholar]
- O’Brien, S.T.; Hubbell, S.P.; Spiro, P.; Condit, R.; Foster, R.B. Diameter, height, crown, and age relationship in eight neotropical tree species. Ecology 1995, 76, 1926–1939. [Google Scholar]
- Chisholm, R.; Pacala, S. Niche and neutral models predict asymptotically equivalent species abundance distributions in high-diversity ecological communities. Proc. Nat. Acad. Sci. USA 2010, 107, 15821–15825. [Google Scholar]
- Seri, E.; Maruvka, Y.E.; Shnerb, N.M. Neutral dynamics and cluster statistics in a tropical forest. Am. Nat. 2012, 180, E161–E173. [Google Scholar]
- Rogers, T.; McKane, A.J.; Rossberg, A.G. Spontaneous genetic clustering in populations of competing organisms. Phys. Biol. 2012, 9. [Google Scholar] [CrossRef]
- García-Martín, H.; Goldenfeld, N. On the origin and robustness of power-law species-area relationships in ecology. Proc. Natl. Acad. Sci. USA 2006, 103, 10310–10315. [Google Scholar]
- Pueyo, S.; He, F.; Zillio, T. The maximum entropy formalism and the idiosyncratic theory of biodiversity. Ecol. Lett. 2007, 10, 1017–1028. [Google Scholar] [CrossRef] [PubMed]
- Jeraldo, P.; Sipos, M.; Chia, N.; Brulc, J.M.; Dhillon, A.S.; Konkel, M.E.; Larson, C.L.; Nelson, K.E.; Qu, A.; Schook, L.B.; et al. Quantification of the relative roles of niche and neutral processes in structuring gastrointestinal microbiomes. Proc. Natl. Acad. Sci. USA 2012, 109, 9692–9698. [Google Scholar] [CrossRef] [PubMed]
- Bowler, M.G.; Kelly, C.K. On the statistical mechanics of species abundance distributions. Theor. Popul. Biol. 2012, 82, 85–91. [Google Scholar] [CrossRef] [PubMed]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Fort, H. Statistical Mechanics Ideas and Techniques Applied to Selected Problems in Ecology. Entropy 2013, 15, 5237-5276. https://doi.org/10.3390/e15125237
Fort H. Statistical Mechanics Ideas and Techniques Applied to Selected Problems in Ecology. Entropy. 2013; 15(12):5237-5276. https://doi.org/10.3390/e15125237
Chicago/Turabian StyleFort, Hugo. 2013. "Statistical Mechanics Ideas and Techniques Applied to Selected Problems in Ecology" Entropy 15, no. 12: 5237-5276. https://doi.org/10.3390/e15125237





