Consistency and Generalization Bounds for Maximum Entropy Density Estimation
Abstract
:1. Introduction
2. Maximum Entropy Density Estimation: Complete Data
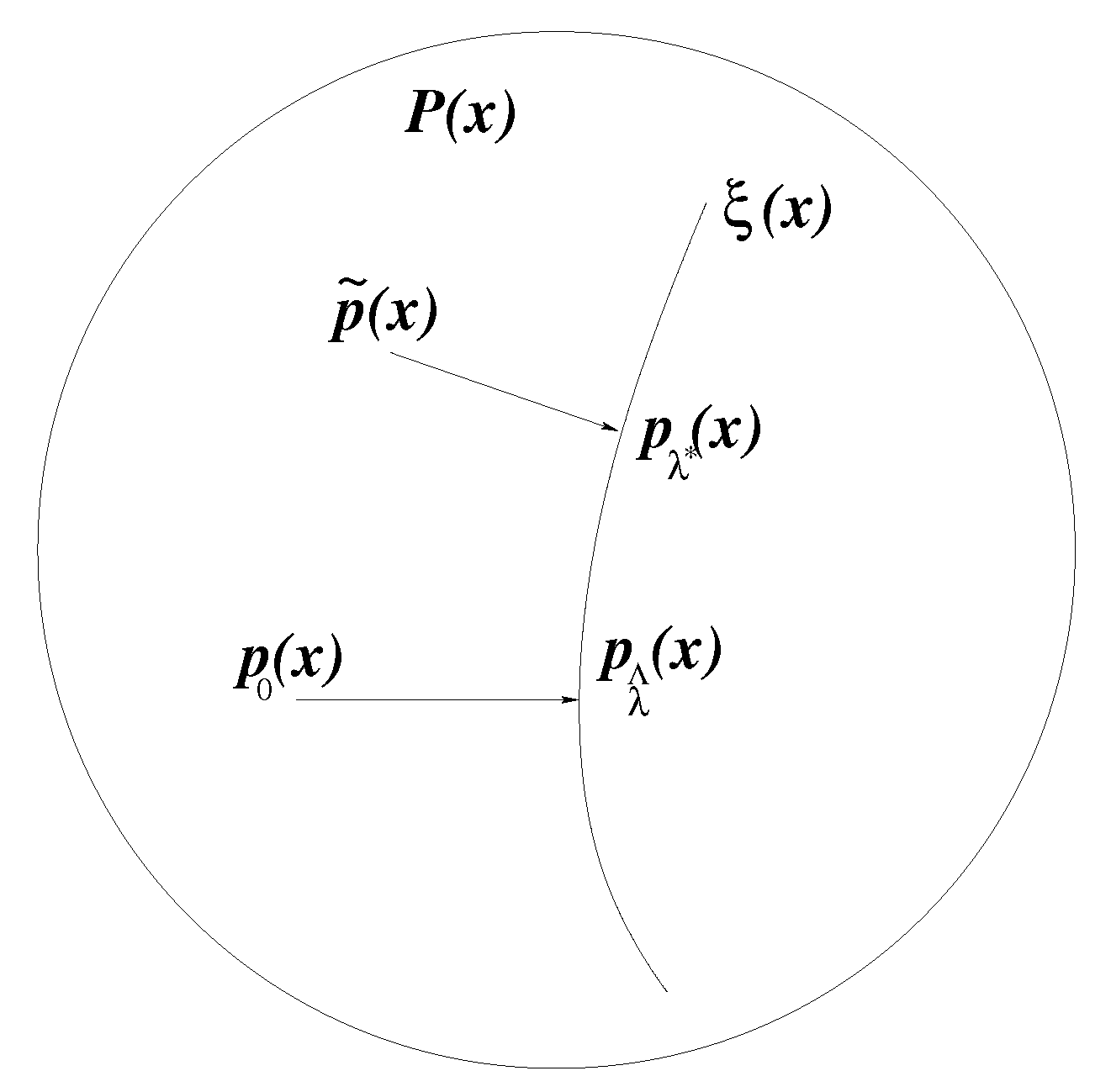
2.1. Consistency and Generalization Bounds of Estimation Error
2.1.1. Maximum Entropy Principle
2.1.2. Regularized Maximum Entropy Principle
3. Maximum Entropy Density Estimation: Incomplete Data
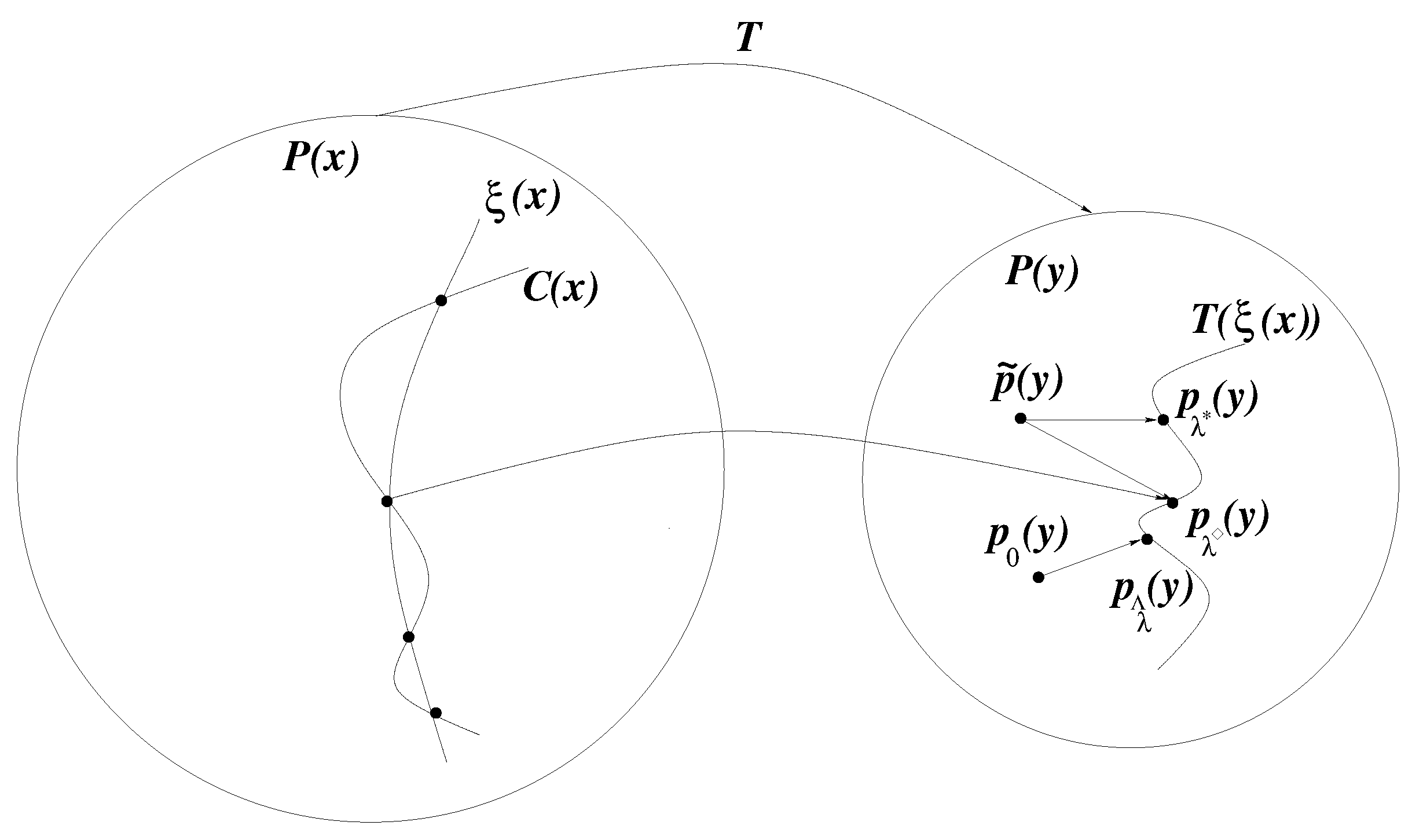
3.1. Consistency and Generalization Bounds for Estimation Error
3.1.1. Maximum Likelihood Estimate
3.1.2. Latent Maximum Entropy Estimate
3.1.3. Maximum a Posteriori Estimate
3.1.4. Regularized Latent Maximum Entropy Estimate
4. Conclusions
Acknowledgments
Conflicts of Interest
Appendix
References
- Jaynes, E. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Della Pietra, S.; Della Pietra, V.; Lafferty, J. Inducing features of random fields. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 380–393. [Google Scholar] [CrossRef]
- Palmieri, F.; Ciuonzo, D. Objective priors from maximum entropy in data classification. Inf. Fusion 2013, 14, 186–198. [Google Scholar] [CrossRef]
- Ziebart, B.; Maas, A.; Bagnell, J.; Dey, A. Maximum Entropy Inverse Reinforcement Learning. In Proceeding of The 23rd National Conference on Artificial Intelligence (AAAI), Chicago, IL, USA, 13–17 July 2008; pp. 1433–1438.
- Wang, S.; Schuurmans, D.; Zhao, Y. The latent maximum entropy principle. ACM Trans. Knowl. Discov. Data 2012, 6, No. 8. 1–42. [Google Scholar] [CrossRef]
- McLachlan, G.; Krishnan, T. The EM Algorithm and Extensions, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2008. [Google Scholar]
- Lehmann, E.L.; Casella, G. Theory of Point Estimation; Springer-Verlag: New York, NY, USA, 1998. [Google Scholar]
- Vapnik, V.; Chervonenkis, A. The necessary and sufficient conditions for consistency in the empirical risk minimization method. Pattern Recognit. Image Anal. 1991, 1, 283–305. [Google Scholar]
- Vapnik, V.N. Statistical Learning Theory; Wiley-Interscience: Hoboken, NJ, USA, 1998. [Google Scholar]
- Barron, A.; Sheu, C. Approximation of density functions by sequences of exponential families. Ann. Stat. 1991, 19, 1347–1369. [Google Scholar] [CrossRef]
- Dudik, M.; Phillips, S.; Schapire, R. Performance Guarantees for Regularized Maximum Entropy Density Estimation. In Proceedings of The 17th Annual Conference on Learning Theory (COLT), Banff, Canada, 1–4 July 2004; pp. 472–486.
- Van de Geer, S. Empirical Processes in M-Estimation; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Jelinek, F. Statistical Methods for Speech Recognition; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Rosenfeld, R. A maximum entropy approach to adaptive statistical language modeling. Comput. Speech Lang. 1996, 10, 187–228. [Google Scholar] [CrossRef]
- Koltchinskii, V.; Panchenko, D. Empirical margin distributions and bounding the generalization error of combined classifiers. Ann. Stat. 2002, 30, 1–50. [Google Scholar]
- Rakhlin, A.; Panchenko, D.; Mukherjee, S. Risk bounds for mixture density estimation. ESAIM: Probab. Stat. 2005, 9, 220–229. [Google Scholar] [CrossRef]
- Csiszar, I. I-divergence geometry of probability distributions and minimization problems. Ann. Probab. 1975, 3, 146–158. [Google Scholar] [CrossRef]
- Barron, A. Approximation and estimation bounds for artificial neural networks. Mach. Learn. 1994, 14, 115–133. [Google Scholar] [CrossRef]
- Zhang, T. Statistical behavior and consistency of classification methods based on convex risk minimization. Ann. Stat. 2004, 32, 56–85. [Google Scholar] [CrossRef]
- Panchenko, D. Class Lecture Notes of MIT 18.465: Statistical Learning Theory; Massachusetts Institute of Technology: Cambridge, MA, USA, 2002. [Google Scholar]
- Zhang, T. Covering number bounds of certain regularized linear function classes. J. Mach. Learn. Res. 2002, 2, 527–550. [Google Scholar]
- Dudley, R. Uniform Central Limit Theorems; Cambridge University Press: New York, NY, USA, 1999. [Google Scholar]
- Wainwright, M.; Jordan, M. Graphical models, exponential families, and variational inference. Found. Trends Mach. Learn. 2008, 1, 1–305. [Google Scholar] [CrossRef]
- Meir, R.; Zhang, T. Generalization error bounds for Bayesian mixture algorithms. J. Mach. Learn. Res. 2003, 4, 839–860. [Google Scholar]
- Chen, S.F.; Rosenfeld, R. A survey of smoothing techniques for ME models. IEEE Trans. Speech Audio Process. 2000, 8, 37–50. [Google Scholar] [CrossRef]
- Borwein, J.; Lewis, A. Convex Analysis and Nonlinear Optimization: Theory and Examples; Springer-Verlag: New York, NY, USA, 2000. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Lebanon, G.; Lafferty, J. Boosting and maximum likelihood for exponential models. Adv. Neural Inf. Process. Syst. 2001, 14, 447–454. [Google Scholar]
- Wang, S.; Schuurmans, D.; Peng, F.; Zhao, Y. Learning mixture models with the regularized latent maximum entropy principle. IEEE Trans. Neural Netw. 2004, 15, 903–916. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T. Leave-one-out bounds for kernel methods. Neural Comput. 2003, 15, 1397–1437. [Google Scholar] [CrossRef]
- Zhang, T. Class-size independent generalization analsysis of some discriminative multi-category classification methods. Adv. Neural Inf. Process. Syst. 2004, 17, 1625–1632. [Google Scholar]
- Wang, S.; Schuurmans, D.; Peng, F.; Zhao, Y. Combining statistical language models via the latent maximum entropy principle. Mach. Learn. J. 2005, 60, 229–250. [Google Scholar] [CrossRef]
- Ledoux, M.; Talagrand, M. Probability in Banach Spaces: Isoperimetry and Processes; Springer-Verlag: Berlin and Heidelberg, Germany, 1991. [Google Scholar]
- Opper, M.; Haussler, D. Worst Case Prediction over Sequences under Log Loss. In The Mathematics of Information Coding, Extraction and Distribution; Cybenko, G., O’Leary, D., Rissanen, J., Eds.; Springer-Verlag: New York, NY, USA, 1998. [Google Scholar]
- Lafferty, J.; Della Pietra, V.; Della Pietra, S. Statistical Learning Algorithms Based on Bregman Distance. In Proceedings of the Canadian Workshop on Information Theory, Toronto, Ontario, Canada, 3–6 June 1997; pp. 77–80.
- Wang, S.; Schuurmans, D. Learning Continuous Latent Variable Models with Bregman Divergences. In Proceedings of The 14th International Conference on Algorithmic Learning Theory (ALT), Sapporo, Japan, 17–19 October 2003; pp. 190–204.
- Bartlett, P. Class Lecture Notes of UC-Berkeley CS281B/Stat241B: Statistical Learning Theory; University of California, Berkeley: Berkeley, CA, USA, 2003. [Google Scholar]
- McDiarmid, C. On the Method of Bounded Differences. In Surveys in Combinatorics; Siemons, J., Ed.; Cambridge University Press: Cambridge, UK, 1989; pp. 148–188. [Google Scholar]
- Van der Vaart, A.; Wellner, J. Weak Convergence and Empirical Processes; Springer-Verlag: New York, NY, USA, 1996. [Google Scholar]
- Zhang, T.; Yu, B. Boosting with early stopping: Convergence and consistency. Ann. Stat. 2005, 33, 1538–1579. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wang, S.; Greiner, R.; Wang, S. Consistency and Generalization Bounds for Maximum Entropy Density Estimation. Entropy 2013, 15, 5439-5463. https://doi.org/10.3390/e15125439
Wang S, Greiner R, Wang S. Consistency and Generalization Bounds for Maximum Entropy Density Estimation. Entropy. 2013; 15(12):5439-5463. https://doi.org/10.3390/e15125439
Chicago/Turabian StyleWang, Shaojun, Russell Greiner, and Shaomin Wang. 2013. "Consistency and Generalization Bounds for Maximum Entropy Density Estimation" Entropy 15, no. 12: 5439-5463. https://doi.org/10.3390/e15125439




