1. Introduction
Classical mechanics, developed in the last few centuries by Galileo, Newton, Lagrange, Hamilton and many others, possesses a rich geometric structure, which was originally unraveled by Poincaré (see, e.g., [
1], for a historical account of these developments). This qualitative approach, widely accepted and explored in the last few decades, has led to many powerful results and
symmetry, broadly understood as invariance under changes in a configuration, has played a central role in many of them [
2,
3,
4,
5,
6]. For instance, the concept of symmetry in Hamiltonian and Lagrangian mechanics has allowed compact formulations of Noether’s theorem, the study of conserved quantities (the momentum maps) and deeper results, such as reduction theory, all of them resulting in a better qualitative understanding of the dynamics of conservative problems.
Non-equilibrium thermodynamics lacks a universally accepted formalism, but it will undoubtedly gain from a similar geometric/qualitative approach, as the one developed for classical mechanics (see [
7] for detailed discussions in this respect). A significant advance in this direction came from GENERIC (General Equations for Non-Equilibrium Reversible-Irreversible Coupling), a complete mathematical framework for the development of non-equilibrium thermodynamical models introduced by Grmela, Öttinger and co-workers [
8,
9,
10]. Based on a solid geometric foundation, GENERIC has opened new avenues to describing in a unifying manner non-equilibrium thermodynamic problems of very diverse class, including hydrodynamics [
10], molecular dynamics [
11], relativistic hydrodynamics [
12], elasticity [
13],
etc. GENERIC expresses the evolution of thermodynamically consistent systems as the sum of a reversible and an irreversible contribution. The reversible part is associated with the total energy through a Poisson operator, just as in the case of Hamiltonian mechanics. The irreversible part, in turn, depends on the total entropy through a symmetric, positive definite bracket. In view of this particular structure, GENERIC can be understood as a generalization of Hamiltonian mechanics to coupled, dissipative systems.
Since GENERIC generalizes Hamiltonian mechanics, it seems natural that the basic notion of symmetry and its associated conserved quantity (as a result of Noether’s theorem) carry on to this extended framework. While symmetry itself has already been addressed in the context of GENERIC ([
10] (section 6.1.6)), we are unaware, however, of an accepted definition in this formalism of the conserved quantity associated with a given symmetry, nor the related Noether’s theorem. The motivation for the current work is precisely to fill this gap, describing precisely the concept of symmetry in GENERIC’s framework and stating the appropriate version of Noether’s theorem.
In the article, we will provide a definition of a momentum map that applies to both finite and infinite dimensional, non-equilibrium thermodynamical problems expressed in the GENERIC formalism. The main use of such a definition will be a theorem proving the preservation of these momentum maps under certain invariance conditions on the energy, that is, the appropriate statement of Noether’s theorem in the context of GENERIC. As expected, the proposed notion of first integral reduces to that of classical Hamiltonian mechanics for the purely reversible case.
While investigating the notion of conserved quantity, we will study the different roles played by the energy and the entropy in generating the reversible and irreversible dynamics of a given system and their relation with the possible symmetries of the evolution equations. We will show that symmetry transformations must lead only to reversible trajectories in the state space, remaining at the same time “orthogonal” to the irreversible dynamics, in a sense made precise below. This geometric insight is explored first in the context of finite dimensional thermodynamical systems and then extended to the more abstract setting of infinite dimensions. It must be noted that the kind of systems we envision are closed and that energy is thus preserved in them. This choice does not preclude the (non-equilibrium) transfer of energy among their subsystems.
To verify that the definition of a momentum map provided is correct, we will work out in detail two examples. Since non-equilibrium thermodynamics has a wide range of applications, including simple rheological models, field theories, cosmology, material modeling, etc., we have chosen to discuss two examples in which symmetries play an important role. The simplicity of the selected examples enables a straightforward derivation of the momentum map and a direct comparison with their conservative (purely Hamiltonian) counterparts. The first one is a simple, finite dimensional model of a nonlinear thermoelastic spring moving inside an insulated cavity. The second example is the infinite dimensional problem of finite strain thermoelasticity. In both cases, we show that the proposed definition of conserved quantity identifies the classical linear and angular momenta, which are also shown to be preserved by the solutions. Both examples are cast in the form of GENERIC models, which is particularly of interest in the infinite dimensional case.
2. GENERIC for Finite Dimensional Problems
The GENERIC framework (General Equations for Non-Equilibrium Reversible-Irreversible Coupling) provides a common mathematical structure for the evolution equations of many thermodynamical systems. As explained in the monograph [
10], thermodynamical systems can be mathematically described by means of a pair of differentiable operators: the first one models the reversible phenomena and the second one, the dissipative effects. When there are no irreversible effects, the GENERIC evolution equations reduce to those of Hamiltonian mechanics, explaining why GENERIC can be understood as a generalization of the latter to coupled thermodynamical problems.
For well-known thermodynamical models, GENERIC might be considered simply as a methodology for writing their evolution equations, which clearly identifies its reversible and irreversible parts. For less understood models, this formalism can be used to check the thermodynamic soundness of the equations, to rule out incorrect terms or even to suggest possible functional expressions for unknown ones. In the present article, we will employ GENERIC only for the first reason, and we will discuss examples whose thermodynamic correctness is not questioned.
We next summarize the basic ingredients of GENERIC in the context of finite dimensional thermodynamical problems. Let
be the state space of a closed thermodynamical system. To describe the evolution in time of the system, we define
and
to be its total energy and entropy, respectively. According to the theory of GENERIC, the time evolution of the system is a curve,
, satisfying the initial condition
, such that:
In this equation, and below, the superposed dot indicates the time derivative; the symbol,
, is the so-called Poisson matrix, and similarly,
is the the friction matrix; finally, the symbol, ∇, denotes the gradient with respect to the state variable.
The Poisson and friction matrices model, respectively, the reversible and irreversible mechanisms of the system dynamics. The matrix,
, must be skew-symmetric, and this property is associated with the conservation of energy in the system; in turn, the matrix,
, must be symmetric and positive-semidefinite, and this is related to the non-monotonic growth of the entropy. The separation of the reversible and irreversible dynamics is expressed by the degeneracy conditions:
One advantage of the formulation (
1) is that, without further conditions, it is simple to prove that such thermodynamical systems possess the following property:
Theorem 1. A thermodynamical model that satisfies (1) and (2) verifies the two laws of thermodynamics, namely: Hamilton’s equations for conservative systems are similar to (
1), the difference being that the term modeling the irreversible effects (the
term) obviously is not included. A more subtle difference, but crucial for the analysis point of view, is that the
matrix in Hamiltonian mechanics must be non-degenerate. This property is important for the definition of conserved quantities.
3. Conserved Quantities in Finite Dimensional Systems
In this section, we explore the geometric characterization of symmetries within the structure afforded by GENERIC. By exploiting the properties of the operators,
and
, the appropriate notion of conserved quantity or momentum map follows, as well as its geometric interpretation. The notation employed closely follows [
14].
Let
G be a Lie group with an associated algebra,
, and its dual
. The exponential map,
, takes elements of the Lie algebra onto the group,
G. Assume the group,
G, acts on the state space,
, via an action,
, and we denote
. In particular, for any
, we can consider the one parameter family of actions,
, of the form
. The tangent of this curve at the origin is given by:
and it is called the infinitesimal generator of the action corresponding to
ξ.
Furthermore, let us assume that the action, Φ, preserves the GENERIC structure, that is:
for any
. The previous two conditions can be written more succinctly as:
where
is the pull-back operation by the action,
.
Extending the classical concept for Hamiltonian systems, we propose the following:
Definition 1. Let
G be a Lie group acting on a state space with actions that preserve the GENERIC structure. Let
be a mapping,
, and define, for any
, the scalar function,
, as:
Then,
is the momentum map associated with the action, Φ, if it satisfies:
In Hamiltonian mechanics, the first of these two conditions uniquely defines the momentum, because the matrix,
, is non-degenerate. Since
is degenerate in GENERIC systems, there are infinite functions in this case that satisfy the first of the two conditions in Equation (
8). Only the two of them correctly define the momentum in general thermodynamic systems.
The identities (
8) geometrically characterize the function,
(or
, in view of the arbitrariness of
ξ): it is the only function that generates “the velocity field” of the symmetry,
i.e., its infinitesimal generator, and does it by means of purely reversible mappings, since it is “orthogonal” to the dissipative mechanisms in the problem.
The definition shows that the function,
, depends on the geometry of the state space and on the thermodynamic phenomena modeled by the evolution Equation (
1), but not on the specific properties of each of the bodies to which these equations can be applied to, which determine the specific forms of
E and
S. Finally, we note that the mapping,
, need not be a conserved quantity of the thermodynamic solution. For that to occur, further conditions need to be met, as shown in the following result:
Theorem 2. Let be the momentum map associated with the action, Φ. If the action preserves the total energy, i.e.
: for any , then is a conserved quantity of the solution. Proof. In Equation (
9), choose
, and take the derivative with respect to
ϵ to obtain:
For any
, we consider the rate of change of the scalar function,
, along a solution of the GENERIC equations. Using the evolution Equation (
1) and the properties (
8) of the momentum map, we obtain:
which identically vanishes in view of Equation (
10). Since
is constant along the solution
for any
ξ, the momentum map
itself must be constant, too. □
The previous result is the appropriate statement of Noether’s theorem in the framework of GENERIC and clearly reveals the different roles played by the energy and the entropy and their relations with the symmetries of the thermodynamic system.
4. A Finite Dimensional Example: The Thermoelastic Pendulum
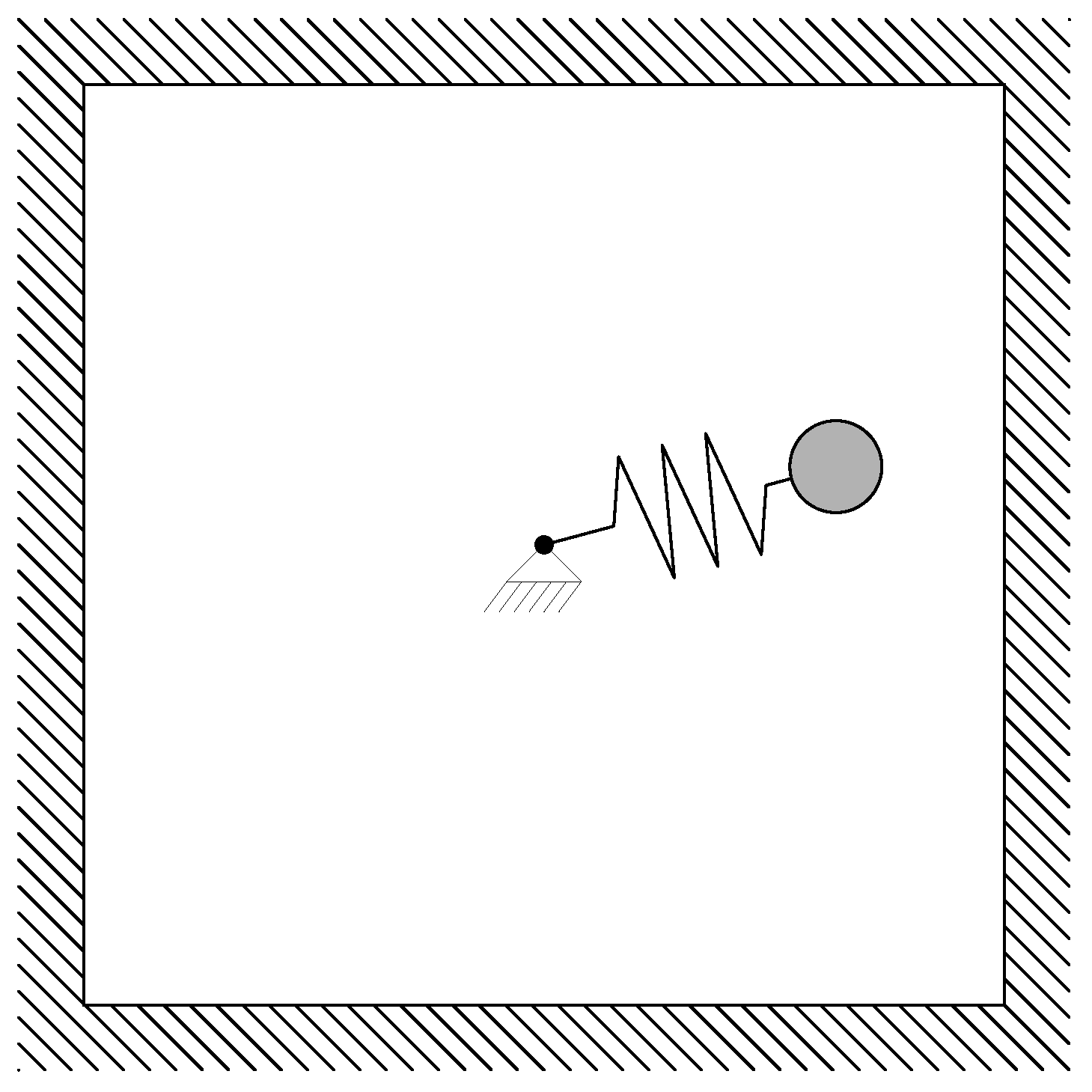
The first example we consider is a simple planar thermoelastic pendulum moving inside an isolated box, as depicted in
Figure 1. The system consists of a thermoelastic spring connecting a fixed point to a moving point mass of value
m. Due to the thermoelastic coupling, changes in the length of the spring produce temperature changes, which might drive heat flowing from the spring into the box, or
vice versa, with flow proportional to the temperature difference and a constant
c.
The state space for this problem is the finite dimensional set:
The position of the point mass is represented by the vector,
, and its momentum by
. The entropy of the spring and the box are denoted, respectively,
and
.
Figure 1.
Thermoelastic pendulum in an insulated cavity.
Figure 1.
Thermoelastic pendulum in an insulated cavity.
The internal energy of the spring and the box are, respectively, the functions
and
. The total energy of the system is the sum of internal energies plus the kinetic energy of the point mass,
i.e.:
Similarly, the total entropy of the system is the sum of the spring and box contributions:
The evolution equations of this nonlinear, finite-dimensional, thermomechanical system are of the form Equation (
1) with discrete operators defined as:
In the previous equation, the temperatures of the spring and the box,
, must be understood as functions of the state variable,
, given by:
Let
be the unit disc. This set is a (commutative) Lie group that acts on the state space of the thermoelastic pendulum via actions of the form:
where
is the operator that rotates by an angle
α vectors in
. If we denote by
the two unit vectors of a Cartesian basis for
, then, for any vector
, the rotation operation reads:
We identify the Lie algebra
of
with the space of vectors in the direction of
, where the symbol “×” denotes the cross product in
. In this way, the infinitesimal generator of the action is the vector field,
, associated with
and defined as:
To prove the existence of a momentum map associated with this action, we first verify that the maps,
, preserve the structure of he GENERIC equations, hence satisfying (
5). Let
be two arbitrary tangent vectors to the state space with components
and
. The push forward of these vectors by the tangent map of the action,
, is:
We start by proving that
, which is equivalent to showing that, for an arbitrary pair of vectors,
:
In view of the specific form Equation (
15) of the Poisson operator,
, and the property of the rotations,
, the left-hand side of this equation can be written as:
which is precisely the invariance that needed to be shown. The proof that the dissipative operator,
, is preserved by the action,
, is identical to the previous one. The details are omitted.
Finally, we verify that the thermoelastic pendulum possesses a momentum map in the sense of Definition 1, which coincides with the classical notion of angular momentum for a purely mechanical pendulum. Let
. To show that this function is a momentum map of the motion, we construct the scalar function:
where the dot stands for the standard Euclidean inner product in
. It only remains to be shown that indeed Equation (
23) is an energy-like function that generates the symmetry orbits as indicated in Equation (
8):
and that it does not generate any irreversible dynamics:
We conclude that the function,
, is the momentum map associated with the rotational action, Φ, which is a symmetry of the thermoelastic pendulum in the sense of Equation (
5).
To verify whether or not the angular momentum is a conserved quantity of the thermoelastic solution, we verify that the action, Φ, preserves the energy. A simple calculation shows that:
since the rotations,
, are isometries. Then, according to Theorem 2, the angular momentum will be preserved along any arbitrary motion of the thermoelastic pendulum.
5. GENERIC in Infinite Dimensional Thermodynamical Systems
In the previous sections, we have discussed conserved quantities in thermodynamical systems with finite dimensional state spaces. The concept of momentum map and the corresponding Noether theorem are extended next to cover systems with infinite dimensional state spaces. For that, the GENERIC formalism is first generalized, and later, the most general definition of a momentum map and Noether’s theorem are stated and proven, respectively.
Let be the state space of a closed thermodynamical system, which can be finite- or infinite-dimensional. If is a state in , then the tangent space of at will be denoted as .
A Poisson bracket is an operation mapping two functionals
into a new functional
. The operation,
, must be bilinear, skew-symmetric and satisfy Leibniz and Jacobi properties. We refer to [
14] for a detailed description of these concepts.
A dissipative bracket is another bilinear operation taking again two functionals, , as above, into a new functional, . In contrast with the Poisson bracket, the dissipative bracket, , must be symmetric and positive semidefinite.
Additionally, in the finite dimensional case, the time evolution of the thermodynamic system requires for its mathematical description a total energy,
, and entropy,
. Then, according to the theory of GENERIC, the state of the system is a curve,
, satisfying the initial condition
, such that, for any functional,
, the following holds:
The time derivative of the arbitrary functional,
, along the solution,
, has two contributions. The first one, associated with the Poisson bracket and the energy, corresponds to the reversible mechanisms in the system. The second part, associated with the dissipative bracket and the entropy is, on the other hand, linked to the dissipation in the model.
The GENERIC framework establishes that every thermodynamically sound model must have evolution equations of the form (
27), provided two additional degeneracy conditions that the bilinear forms must verify, namely:
for every functional,
.
Without any further conditions on the mathematical structure of the brackets, it is simple to prove that such thermodynamical systems possess the following property:
Theorem 3. A thermodynamical model defined by Equation (27) that satisfies the degeneracy conditions (28) verifies the two laws of thermodynamics, that is: 7. A Infinite Dimensional Example: Finite Strain Thermoelasticity
The second example we study is the infinite dimensional problem of finite strain thermoelasticity. A different approach to this problem in the context of GENERIC has been presented in [
15].
A thermoelastic body, , is an open bounded set in with boundary and points labeled as . At every instant , the body deforms under a configuration, , mapping the reference placement to the current placement of the body. The motion of the body is the one-parameter curve of configurations , which will be assumed to be smooth enough. The deformation gradient, , is the tangent map of the motion. The body has a reference density , and the thermodynamical state of each point is completed with its momentum, , and its entropy per unit of reference volume, η. Both of these quantities depend, in general, on the particle, , and the time instant, t.
The thermoelastic behavior of the body is described by means of the internal energy density . Taking into consideration frame invariance restrictions on the functional form of e, it can be shown with standard arguments that the internal energy can only depend on the deformation gradient through its symmetric part. Defining the right Cauchy–Green deformation tensor as , we can conclude that the internal energy must be of the form .
The configuration space of the thermoelastic body is defined as:
Under the previous definitions, the total energy,
, and entropy,
, of the body,
, are, respectively:
The time evolution of the state variables
at every point of the thermoelastic body is governed by the balance of linear momentum and energy. Let
denote the symmetric Piola–Kirchhoff stress tensor. If the body,
, is thermally isolated and there are no external forces acting on it, these two balance laws reduce, respectively, to:
where
is the heat flux per unit of reference area,
is the material divergence operator, and
is the material temperature field defined as
. The heat flux is assumed to satisfy Fourier’s law: given a symmetric, positive definite tensor of conductivities
, the material formulation of the heat conduction equation reads:
where
is the material gradient operator. We note that in the two previous equations the temperature field is a function of the deformation gradient and the entropy density.
The complete description of the evolution problem of thermoelasticity requires initial conditions for the state variables at every point
:
and the boundary conditions at every point
:
where
is the outward normal to the boundary of the body at point
.
To study momentum maps on a thermoelastic body within the context of GENERIC, we first postulate the Poisson and dissipative operators and then verify that they give rise to the initial value problem previously described. For any two functionals,
and
, we define the Poisson bracket to be identical to the canonical bracket of Hamiltonian mechanics (see [
16]):
In the previous equation and below, the notation,
, denotes the inner product:
for every pair of scalars, or vectors, or tensors,
, defined over
. The dissipative bracket is defined to be, for any two functionals,
, as above, of the form:
In view of the properties of the material conductivity tensor,
, the dissipative bracket is symmetric and positive semidefinite.
The functional derivatives of the total energy and entropy can be calculated in a straightforward manner to be:
The symbol,
, denotes the Dirac delta distribution on the body boundary. With the previous functional derivatives, the degeneracy conditions
can be easily verified. Finally, by replacing expressions (
42)–(
45) in main GENERIC Equation (
27), we obtain that the time derivative of any functional,
, can be calculated as:
On the other hand, by definition, the time derivative of
can also be written as:
Integrating by parts the dissipative bracket in Equation (
46) and identifying the terms multiplying the arbitrary functional derivatives of
, we obtain:
which correspond to the evolution Equation (
38), the definition of momentum density and the boundary conditions on tractions and heat flux.
To study the symmetries of the coupled thermoelastic problem, we consider two different actions on the state space,
. The first one is the action,
Φ, of
on
by means of translations of the form:
with infinitesimal generator:
for any
. In the purely mechanical theory of deformable bodies, this action is associated with the classical linear momentum:
which is a first integral of the motion if the Hamiltonian is invariant under the action, Φ. The same conservation law holds for the thermoelastic problem, as we will now show by verifying the conditions of Theorem 4.
As a first step, we calculate the functional derivatives of the composed map: for every functional,
, the functional derivatives of
, with respect to the state variables are:
Using these expressions, it is straightforward to verify the invariance of the Poisson operator (
42) under the action, Φ. To show the invariance of the dissipative operator (
44), in addition to (
51), we need the following relation:
with
being an arbitrary functional as above. Using the previous identity and Equation (
51), it follows that:
which proves that the action preserves the dissipative bracket.
The scalar function:
can be employed to verify the two conditions in Equation (
32). To check the first one, the two following quantities are calculated, for any functional,
:
which are identical. The second identity in Equation (
32) is trivially satisfied. Thus, according to Definition 2, the function,
, is the momentum map associated with the action (
48). Furthermore, since the energy depends on the configuration only through the Cauchy–Green tensor, it is invariant under the action of Φ; hence, according to Theorem 4, the linear momentum,
, is the first integral in the evolution of the thermoelastic solid.
The second relevant action on the state space is Ψ, defined as the action of the special orthogonal group, SO(3):
on
by means of finite rotations:
Identifying
with the lie algebra of SO(3), the infinitesimal generator of this action can be calculated to be, for any
, of the form:
where the symbol “×” denotes the standard cross product for vectors in
. Associated with the action, Ψ, is the classical angular momentum:
which, in Hamiltonian mechanics, is constant if
Ψ preserves the total energy.
The analysis of the rotational action (
57) and its attendant symmetry follows the same arguments employed for the translational action. In the purely mechanical case, it is known that the function,
, is associated with the action (
57). In order to extend the same conclusion to the coupled thermomechanical problem, we need to verify first, based on the conditions of Definition 2, that
Ψ preserves the GENERIC structure. To that end, we note the following relations for the functional derivatives of an arbitrary composite functional,
, are straightforwardly obtained:
Next, to show that the Poisson bracket is preserved by the action, Ψ, we verify the first condition in Equation (
30) using the properties of the elements in SO(3):
Since the dissipative bracket only depends on the functional derivatives with respect to the specific entropy and the action, Ψ, preserves them, the same argument employed in Equation (
53) is valid for the rotational action, and we conclude that the two operators in the GENERIC evolution equations are preserved by the action.
To conclude that
is the momentum map associated with the rotational action, Ψ, we still need to verify the conditions (
32). For that purpose we define, for every
, the functional:
Then, we calculate the directional derivatives of an arbitrary functional,
:
which are identical, due to the skew-symmetry of the cross product, proving the first of the two conditions. The condition
follows from the form of the dissipative bracket and the fact that the momentum map does not depend on the specific entropy. Since both conditions are satisfied, the angular momentum (
59) is the appropriate momentum map associated with the action (
57).
Finally, to verify that the angular momentum is a conserved quantity of the thermoelastic solution, it suffices, according to Theorem 4, to verify the invariance of the energy with respect to Ψ. Using, again, the property
for rotations
, it follows that:
We conclude that the angular momentum is a conserved quantity of the finite strain, thermoelastic problem.