Capacity Region of a New Bus Communication Model
Abstract
:1. Introduction
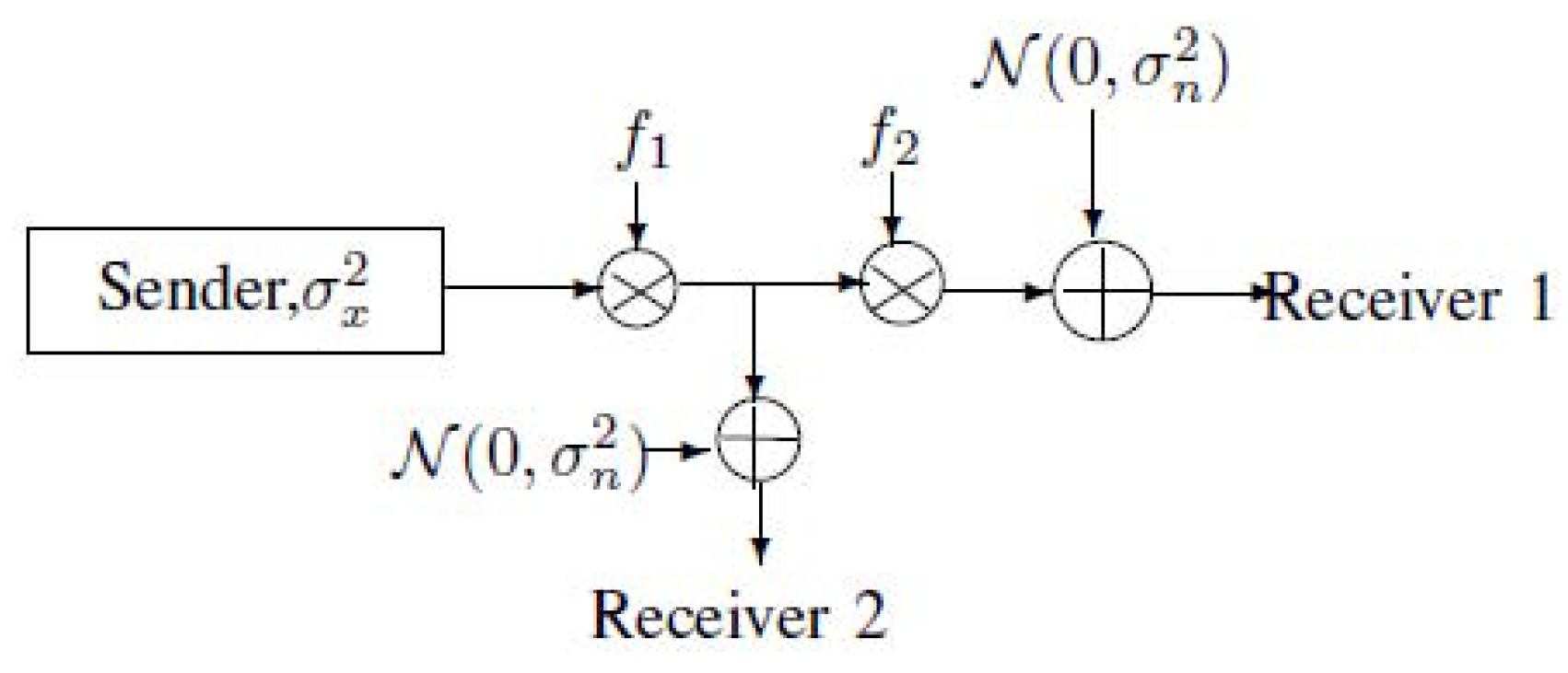
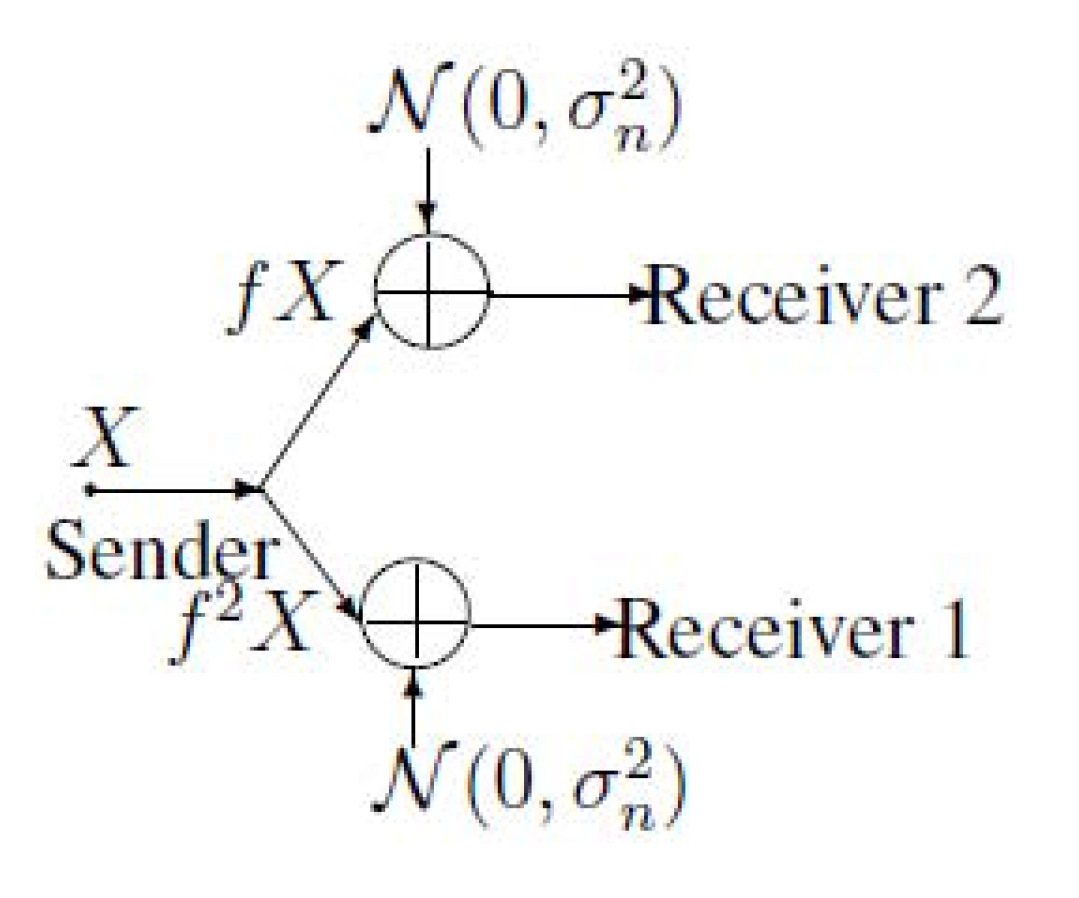
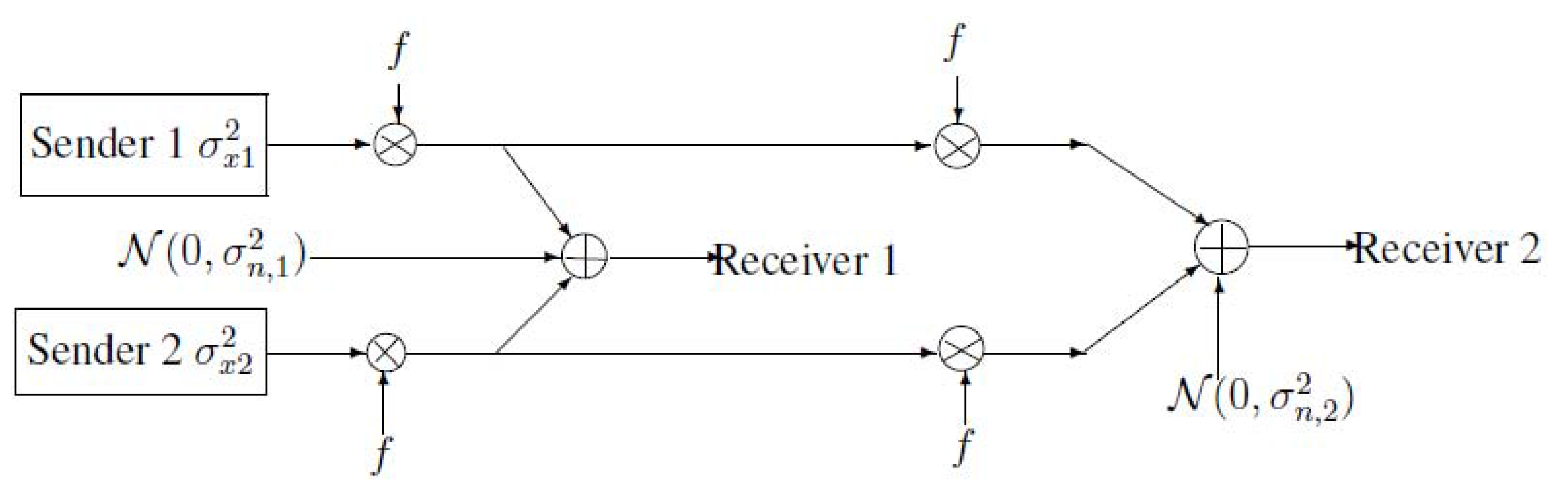
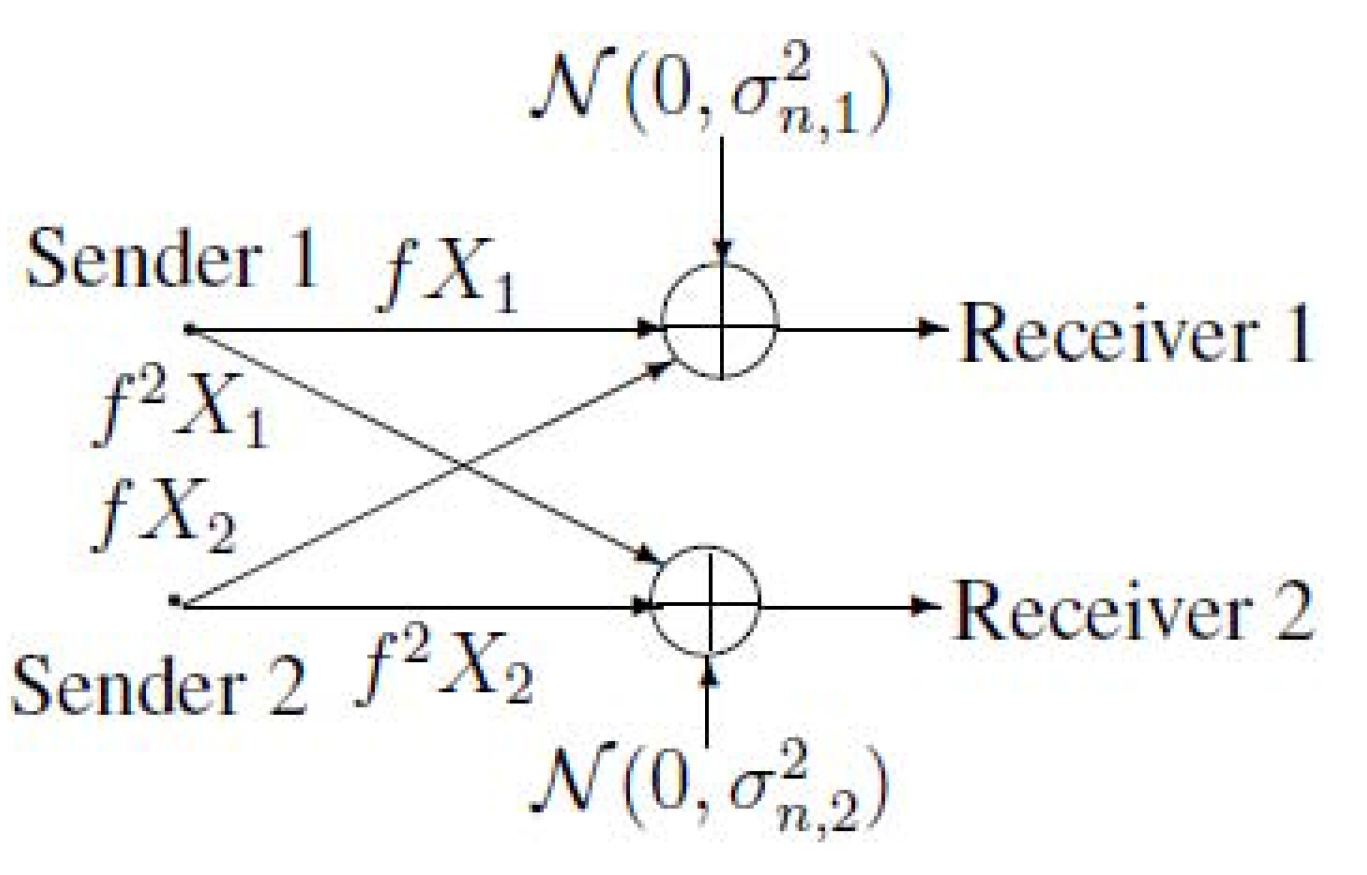

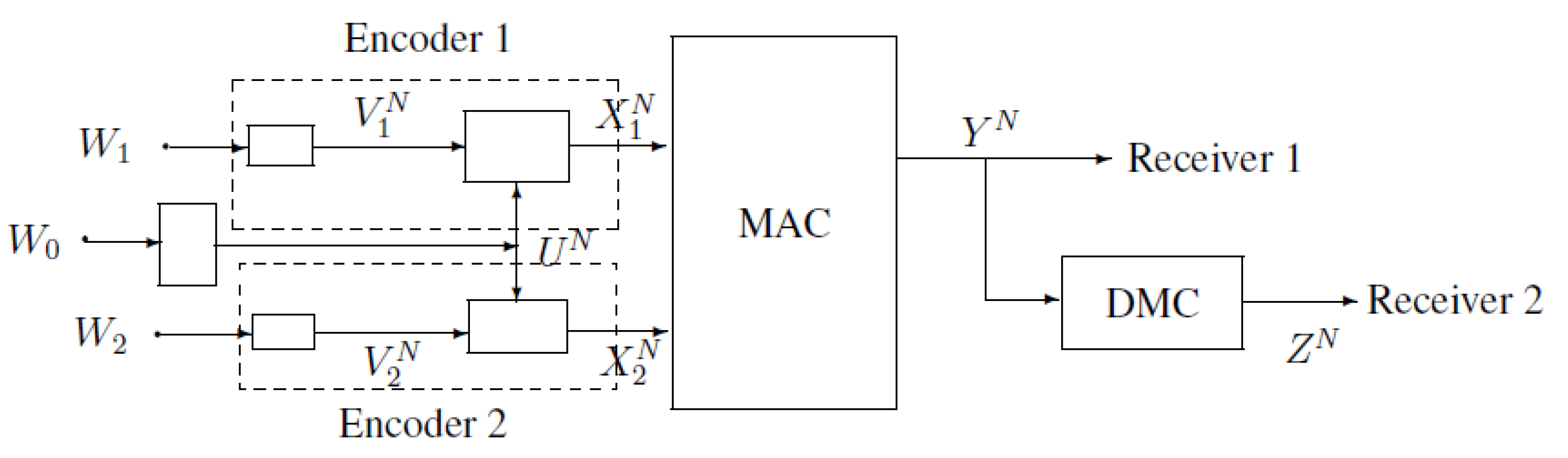
2. Notations, Definitions and the Main Results of MAC-DBC
3. A Gaussian Example of MAC-DBC and the Capacity Region of the Model of Figure 4
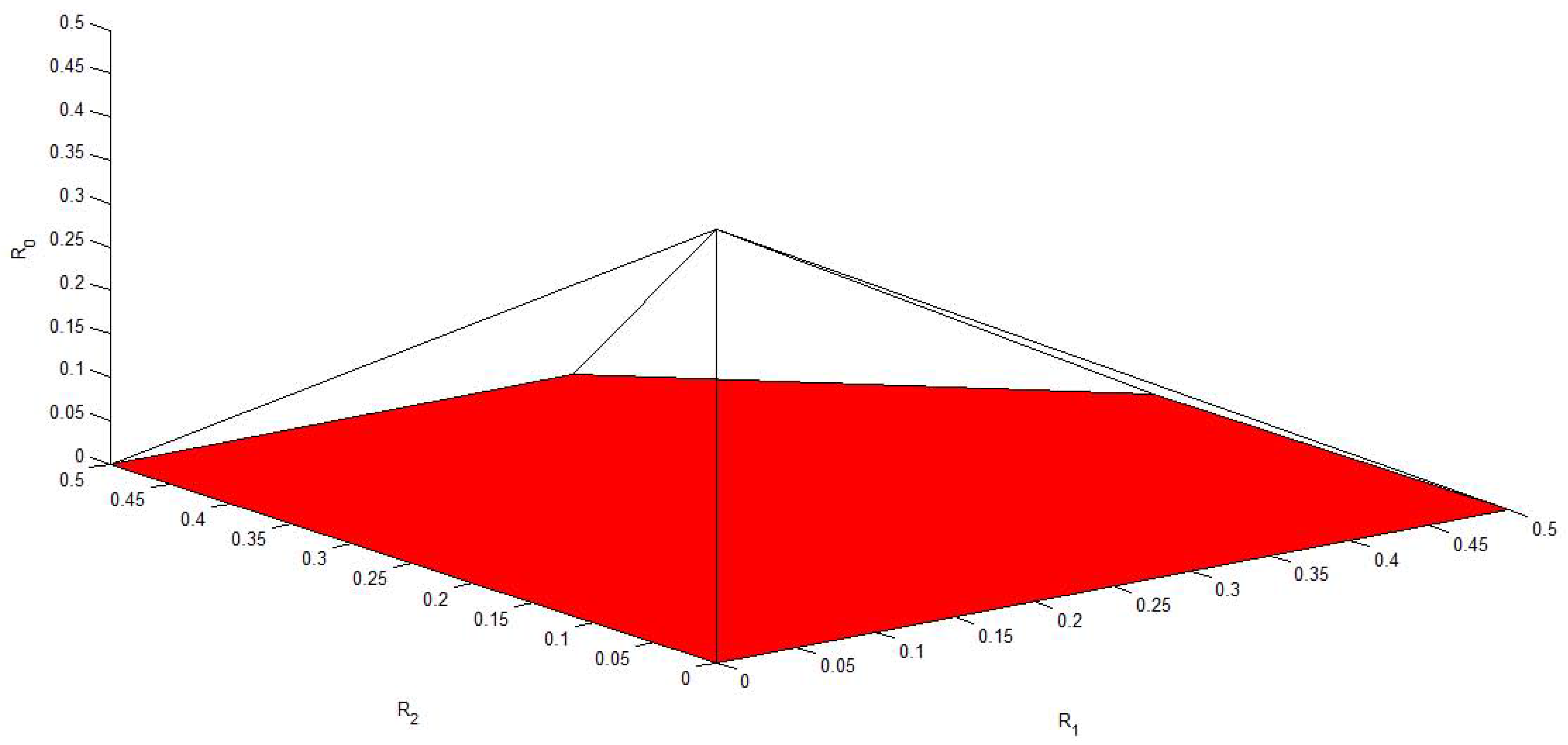
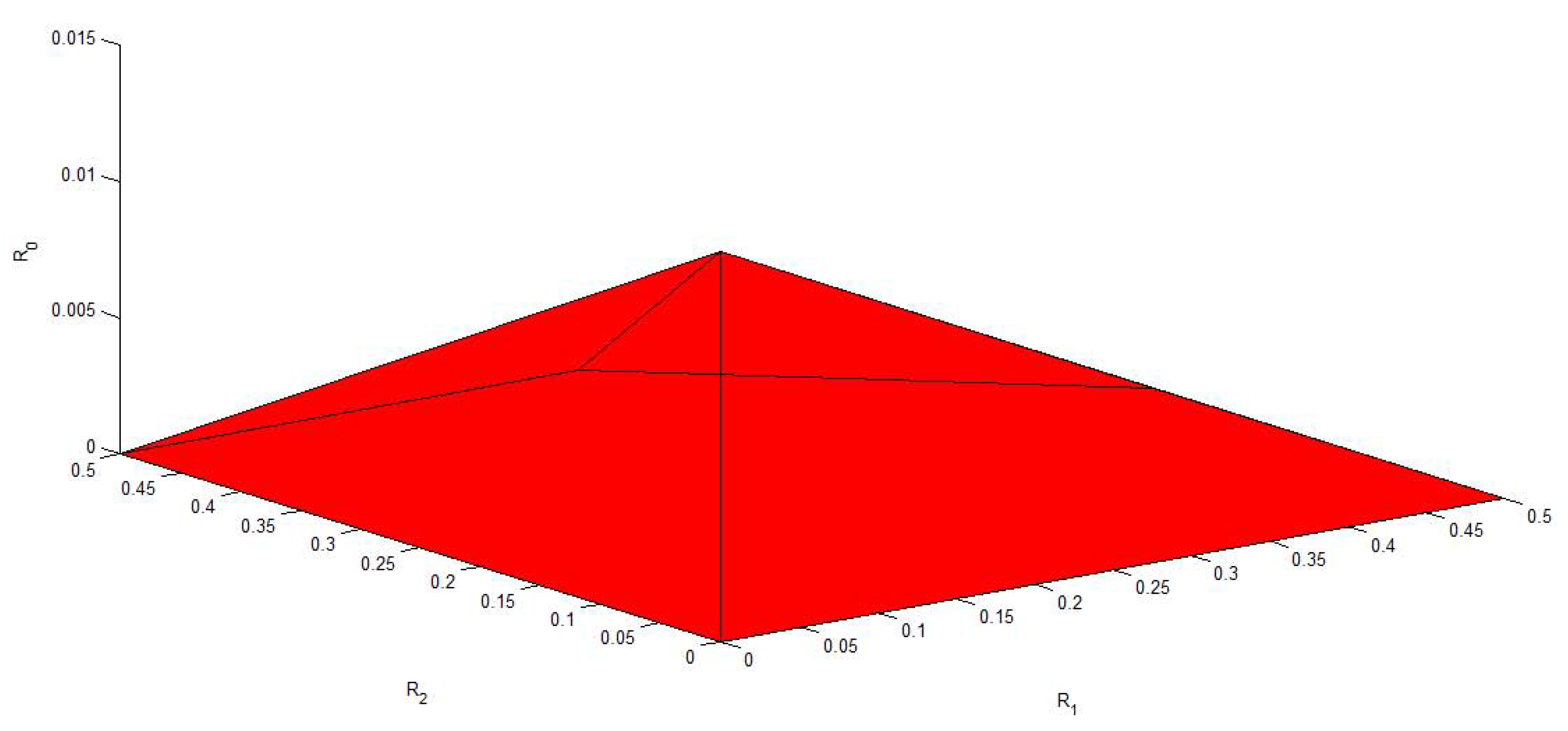
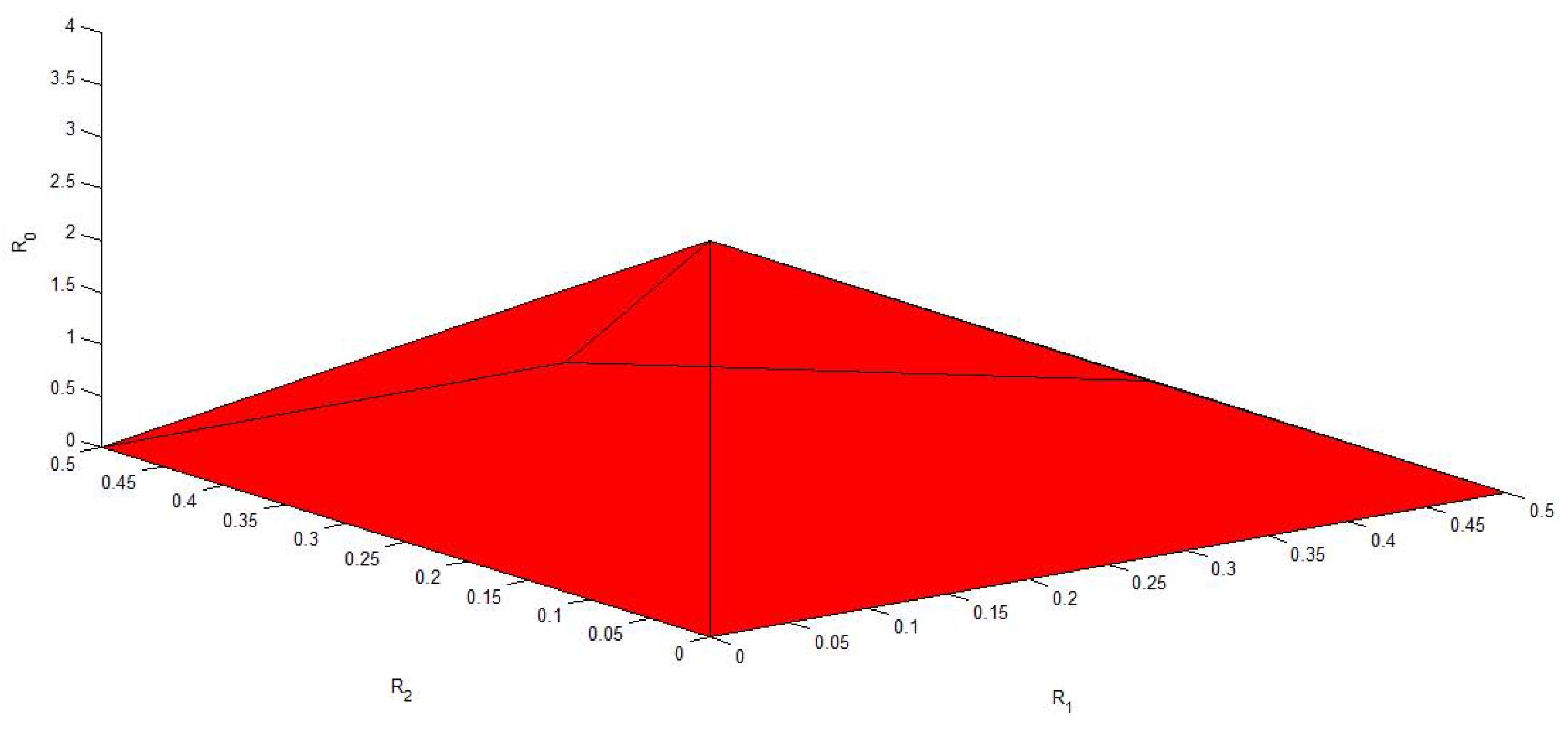
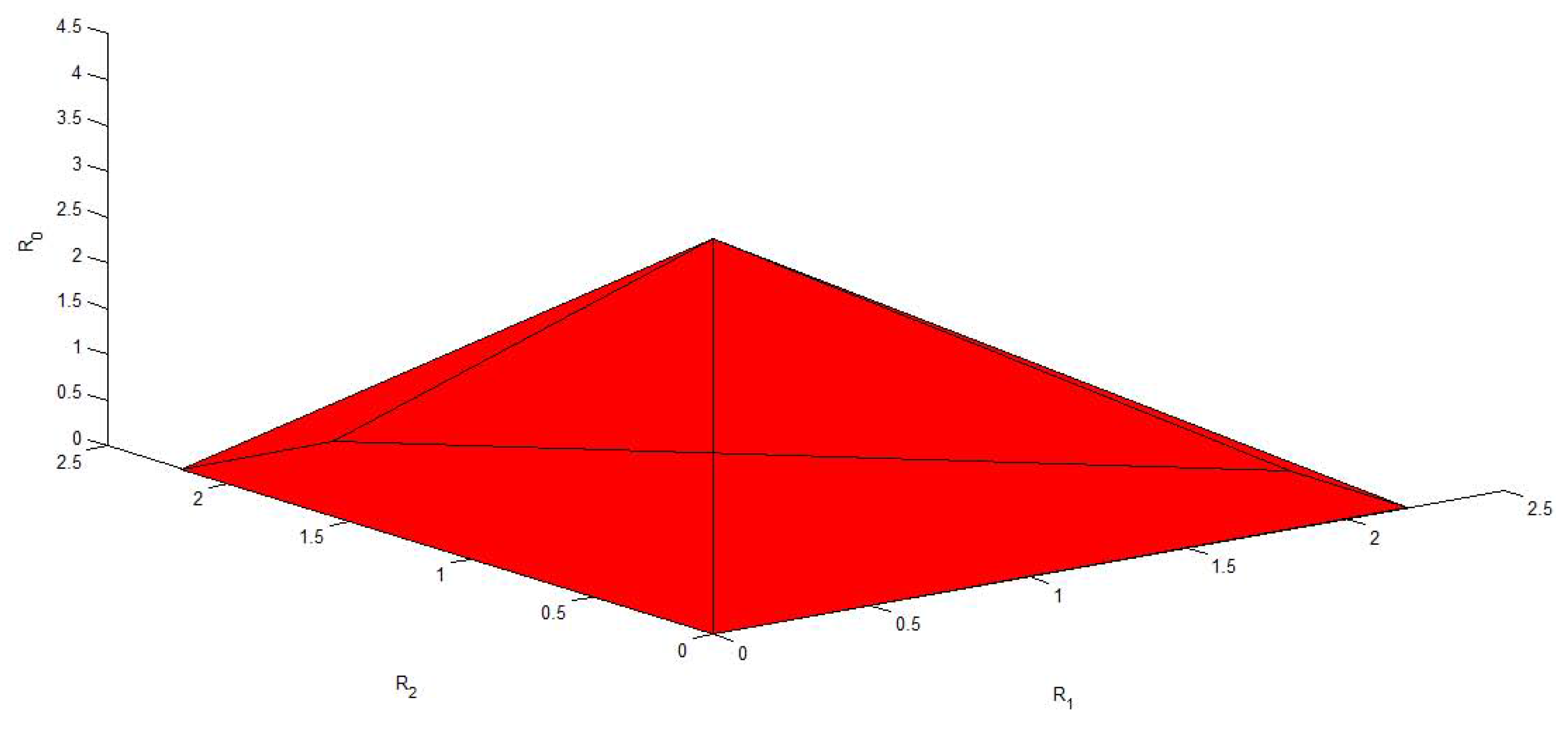
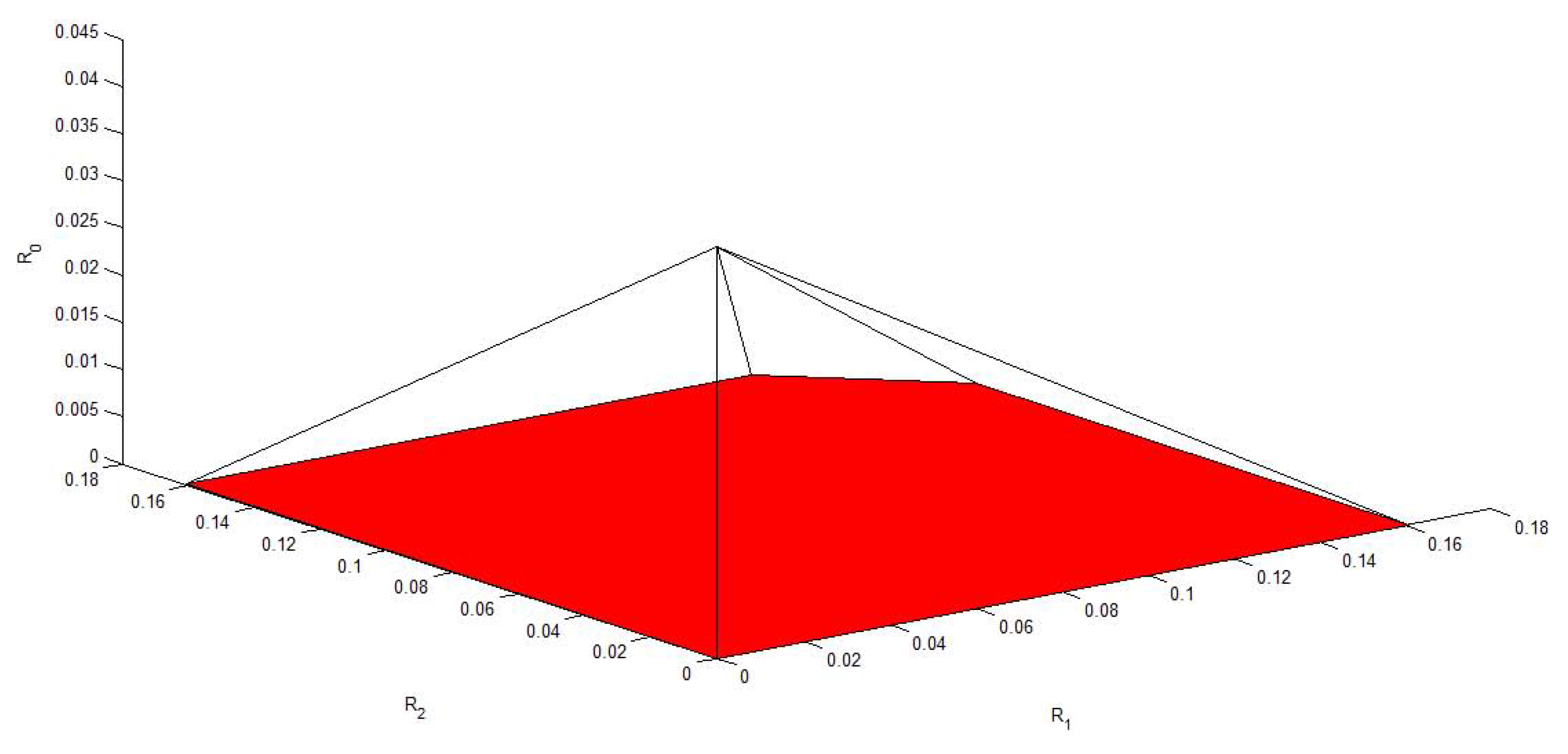
4. Conclusions
Acknowledgement
References
- Lampe, L.; Schober, R.; Yiu, S. Distributed space-time block coding for multihop transmission in power line communication networks. IEEE J. Select. Areas Commun. 2006, 24, 1389–1400. [Google Scholar] [CrossRef]
- Bumiller, G.; Lampe, L.; Hrasnica, H. Power line communications for large-scale control and automation systems. IEEE Commun. Mag. 2010, 48, 106–113. [Google Scholar] [CrossRef]
- Lampe, L.; Han Vinck, A.J. On cooperative coding for narrow band PLC networks. Int. J. Electron. Commun. (AEÜ) 2011, 8, 681–687. [Google Scholar] [CrossRef]
- Balakirsky, V.; Vinck, A. Potential performance of PLC systems composed of several communication links. Intl. Symp. Power Line Commun. Appl. Vancouver 2005, 10, 12–16. [Google Scholar]
- Johansson, M.; Nielsen, L. Vehicle applications of controller area network. Tech. Rep. 2003, 7, 27–52. [Google Scholar]
- Cover, T.M. Broadcast channels. IEEE Trans. Inf. Theory 1972, 18, 2–14. [Google Scholar] [CrossRef]
- Körner, J.; Marton, K. General broadcast channels with degraded message sets. IEEE Trans. Inf. Theory 1977, 23, 60–64. [Google Scholar] [CrossRef]
- Gallager, R.G. Capacity and coding for degraded broadcast channels. Probl. Inf. Transm. 1974, 10, 3–14. [Google Scholar]
- Bergmans, P.P. A simple converse for broadcast channels with additive white Gaussian noise. IEEE Trans. Inf. Theory 1974, 20, 279–280. [Google Scholar] [CrossRef]
- Bergmans, P.P. Random coding theorem for broadcast channels with degraded components. IEEE Trans. Inf. Theory 1973, 19, 197–207. [Google Scholar] [CrossRef]
- El Gamal, A.; Cover, T.M. Multiple user information theory. Proc. IEEE 1980, 68, 1466–1483. [Google Scholar] [CrossRef]
- Ahlswede, R. Multiway Communication Channels. In Proceedings of the 2nd International Symposium Information Theory, Tsahkadsor, Armenia, /hlconference date, day and month 1971; pp. 23–52.
- Liao, H.H.J. Multiple access channels. Ph.D. Thesis, University of Hawaii, Honolulu, 1972. [Google Scholar]
- Csisza´r, I.; Körner, J. Information Theory. Coding Theorems for Discrete Memoryless Systems; Academic: London, UK, 1981. [Google Scholar]
- El Gamal, A.; Kim, Y. Lecture notes on network information theory. Available online: http://arxiv.org/abs/1001.3404 (accessed on 20 January 2010).
- Yeung, R.W. Information Theory and Network Coding; Springer: New York, NY, USA, 1981. [Google Scholar]
- Liang, Y.; Poor, H.V. Multiple-access channels with confidential messages. IEEE Trans. Inf. Theory 2008, 54, 976–1002. [Google Scholar] [CrossRef]
Appendix
A. Proof of the Converse Part of Theorem 2
B. Proof of the Direct Part of Theorem 2
- Given a probability mass function, , for any , let be the strong typical set of all , such that for all , where is the number of occurences of the letter v in the . We say that the sequences, , are V-typical.
- Analogously, given a joint probability mass function, , for any , let be the joint strong typical set of all pairs , such that for all and , where is the number of occurences of in the pair of sequences . We say that the pairs of sequences, are -typical.
- Moreover, is called -generated by iff is V- typical and . For any given , define .
- Lemma 1 For any ,where as .
- For a given , generate a corresponding i.i.d., according to the probability mass function .
- For a given , generate a corresponding i.i.d., according to the probability mass function .
- For a given , generate a corresponding i.i.d., according to the probability mass function .
- is generated according to a new discrete memoryless channel (DMC), with inputs and , and output . The transition probability of this new DMC is .Similarly, is generated according to a new discrete memoryless channel (DMC), with inputs and , and output . The transition probability of this new DMC is .
- (Receiver 1) Receiver 1 declares that messages, , and , are sent if they are the unique messages, such that , otherwise, it declares an error.
- (Receiver 2) Receiver 2 declares that a message is sent if it is the unique message, such that ; otherwise it declares an error.
2.3.1.
2.3.2.
C. Proof of the Convexity of
D. Size Constraints of the Auxiliary Random Variables in Theorem 2
E. Proof of Theorem 3
E.1. Proof of the Achievability
E.2. Proof of the Converse
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Dai, B.; Vinck, A.J.H.; Luo, Y.; Zhuang, Z. Capacity Region of a New Bus Communication Model. Entropy 2013, 15, 678-697. https://doi.org/10.3390/e15020678
Dai B, Vinck AJH, Luo Y, Zhuang Z. Capacity Region of a New Bus Communication Model. Entropy. 2013; 15(2):678-697. https://doi.org/10.3390/e15020678
Chicago/Turabian StyleDai, Bin, A. J. Han Vinck, Yuan Luo, and Zhuojun Zhuang. 2013. "Capacity Region of a New Bus Communication Model" Entropy 15, no. 2: 678-697. https://doi.org/10.3390/e15020678



