Truncation Effects of Shift Function Methods in Bulk Water Systems
Abstract
:1. Introduction
2. Experimental
3. Results and Discussions
3.1. Bulk Water
3.1.1. Potential Energy
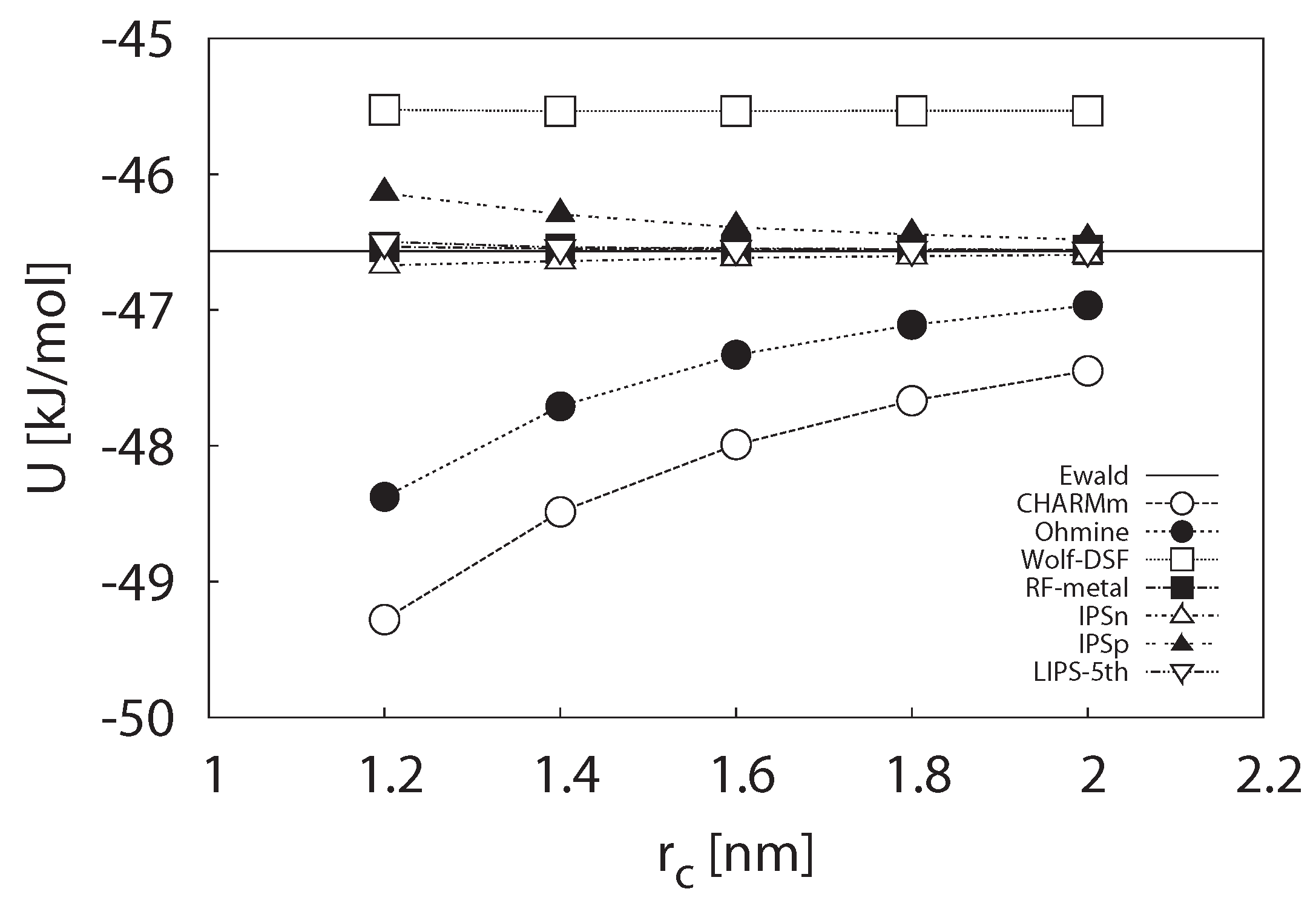
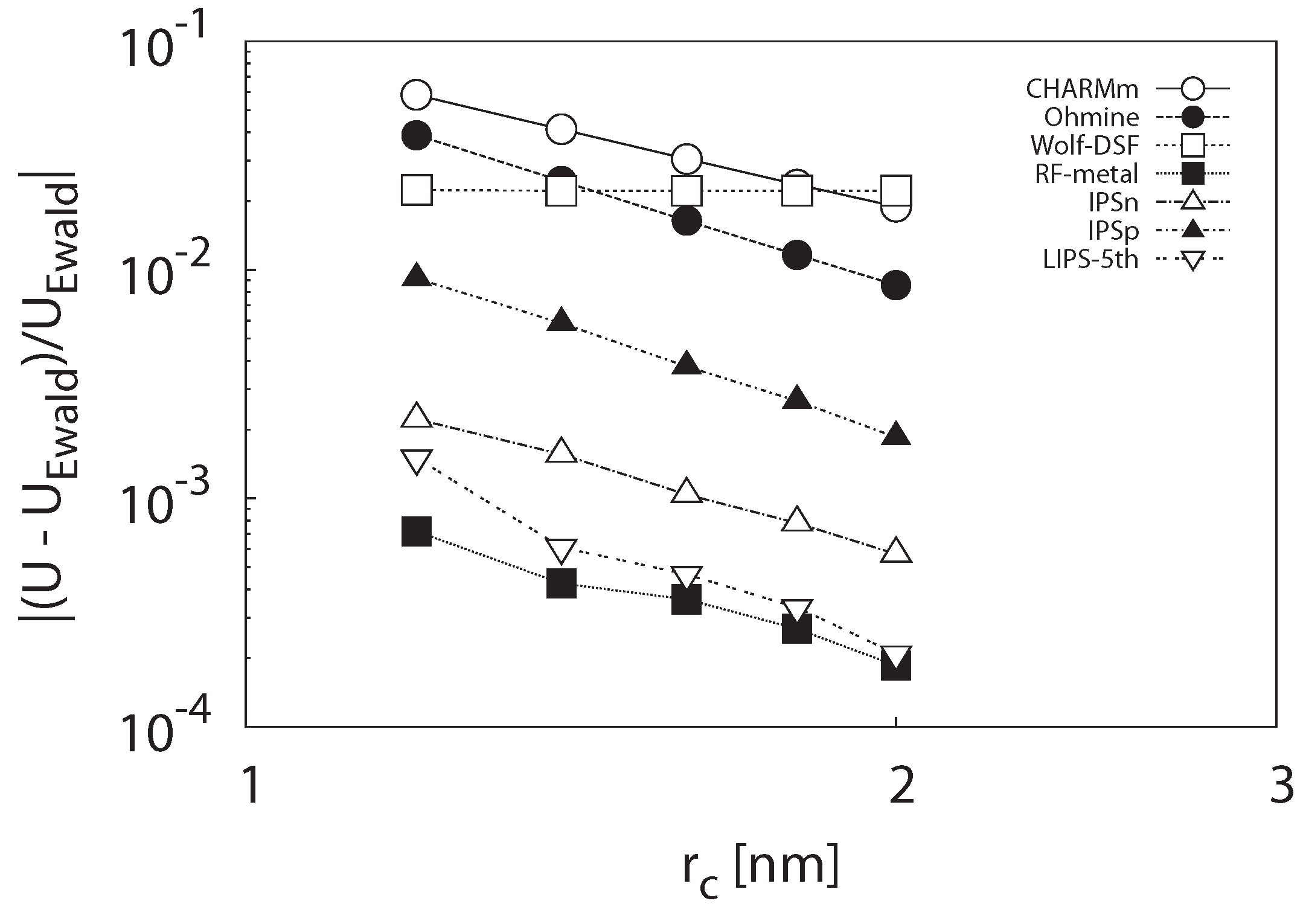
3.1.2. Self-Diffusion Coefficient
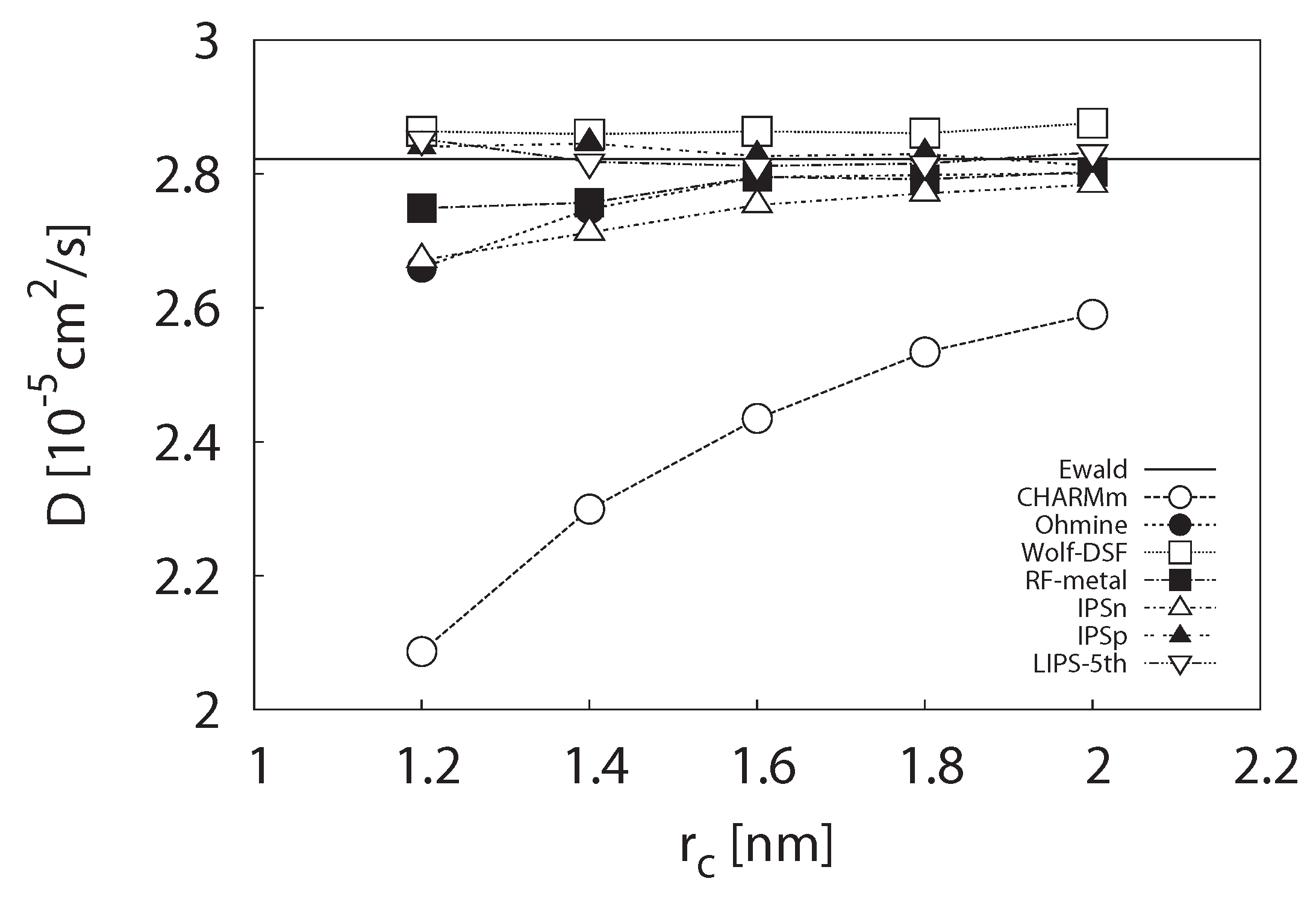
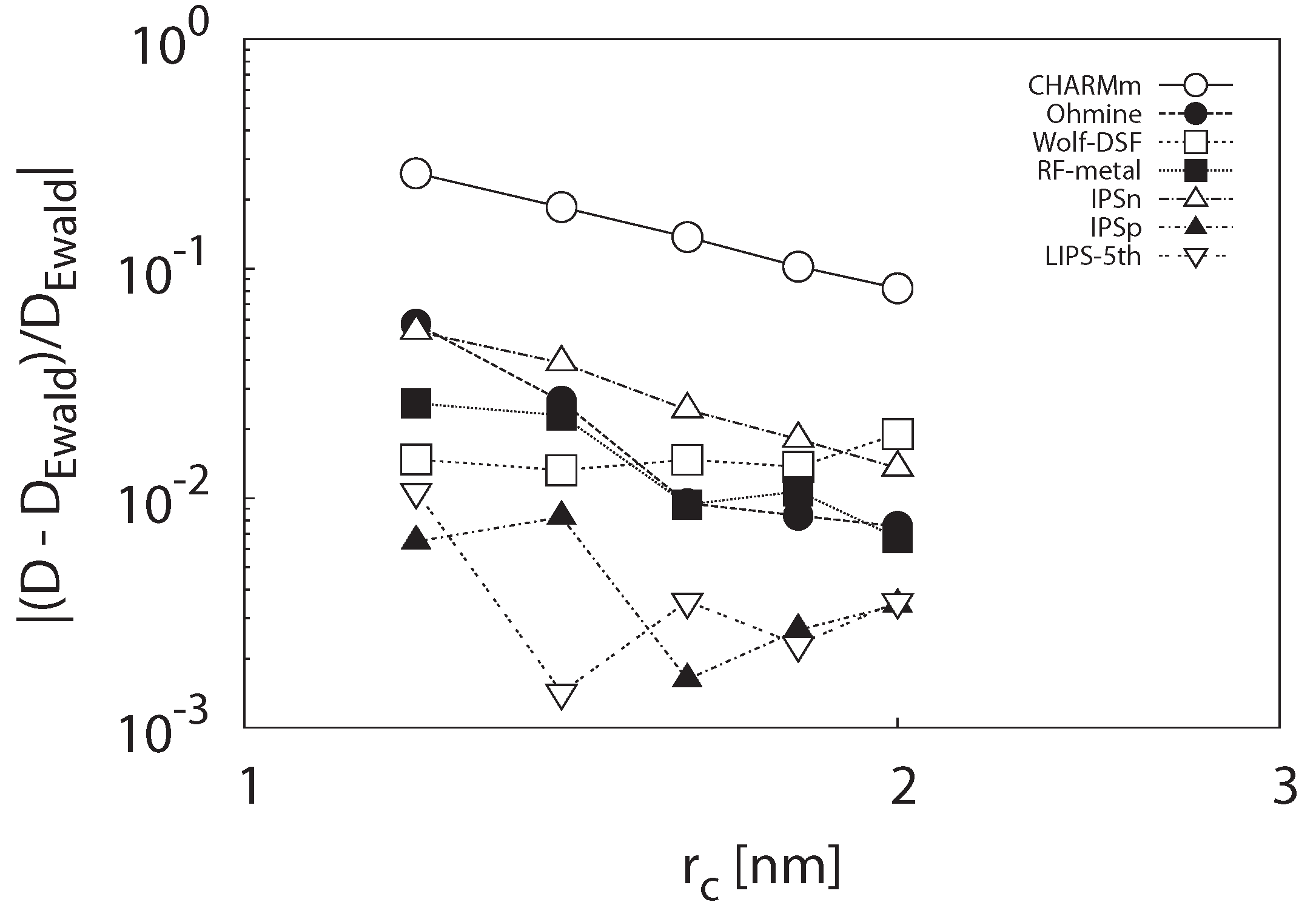
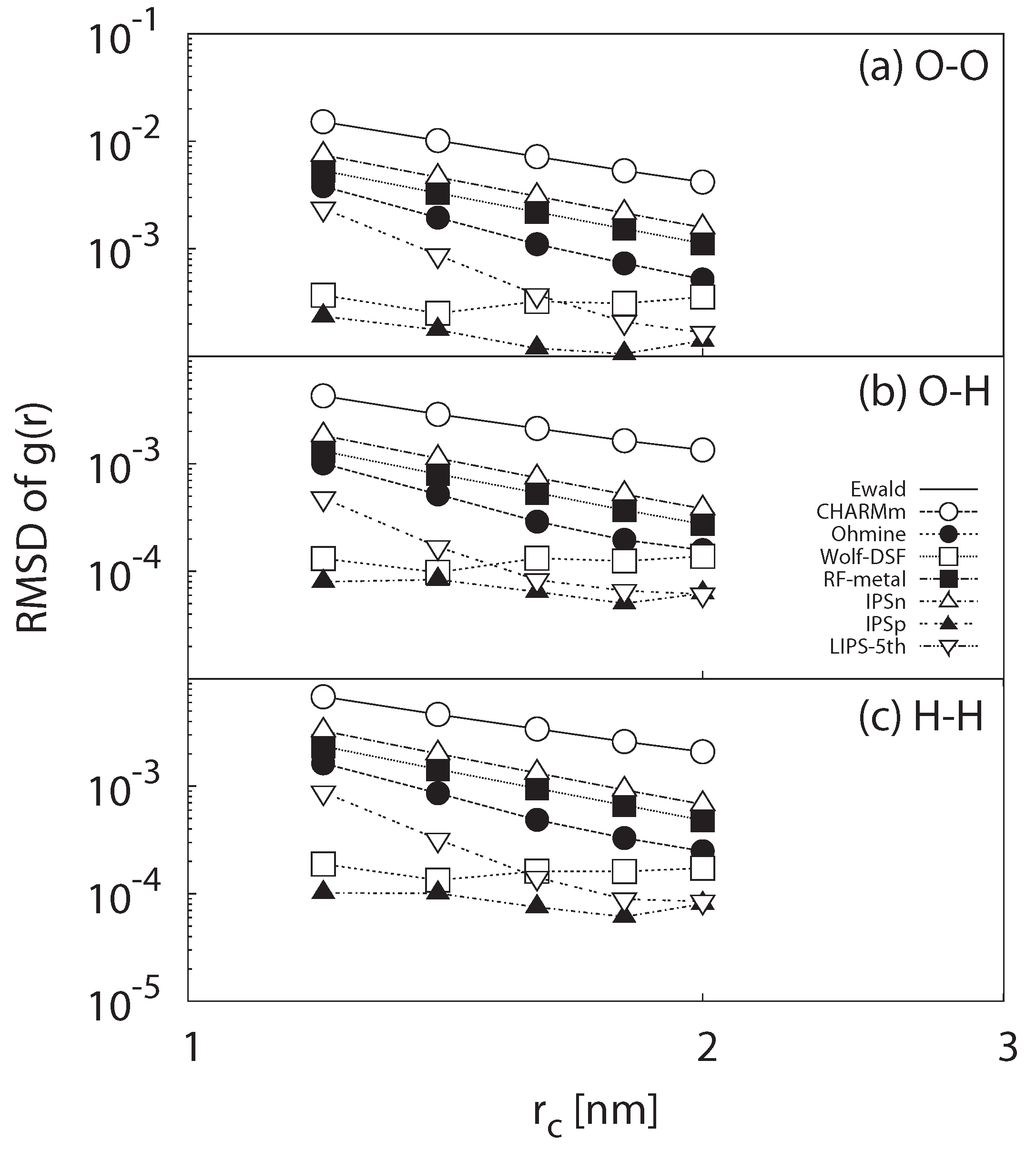
3.1.3. Radial Distribution Function

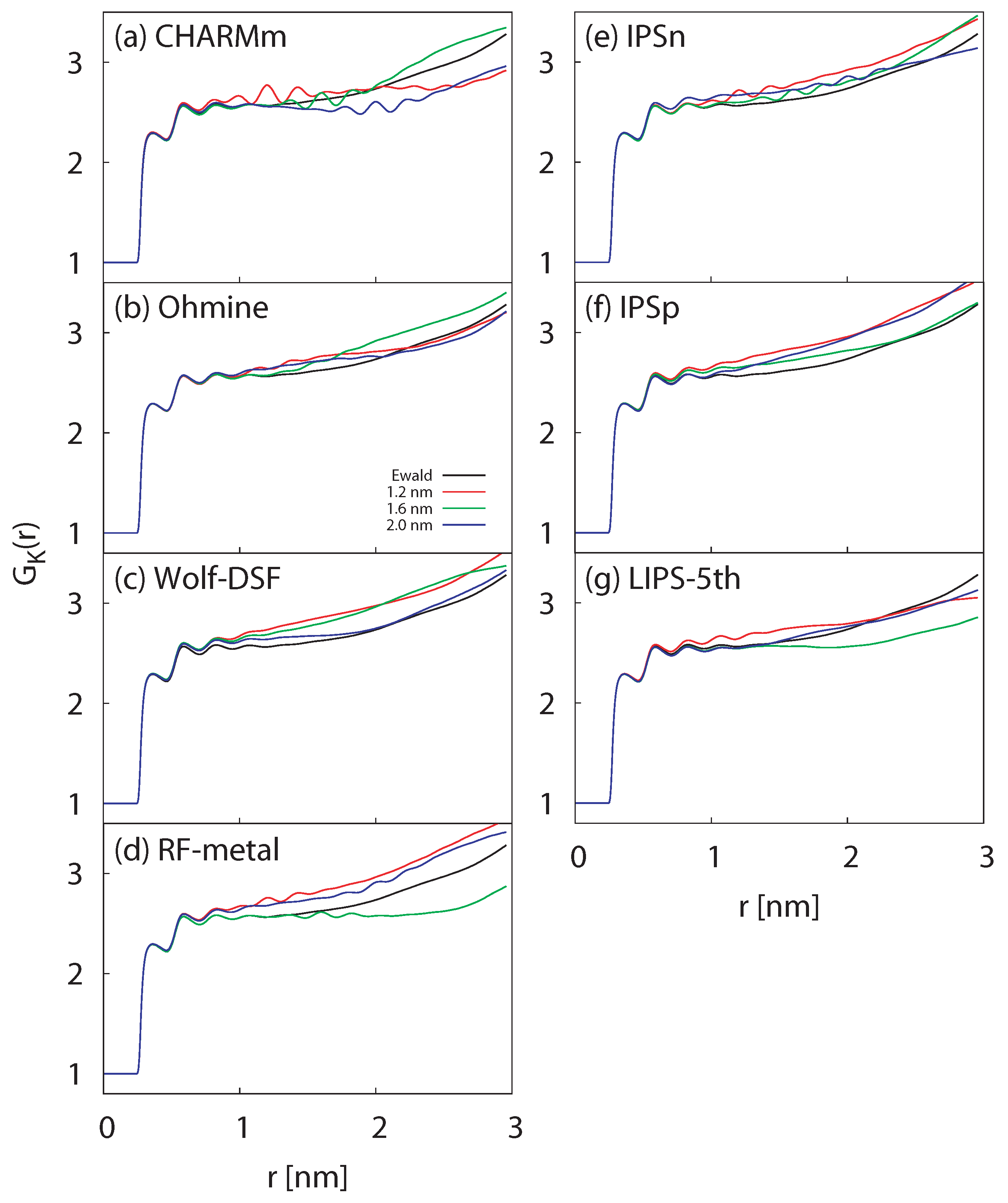
3.1.4. Dipole-Dipole Correlation
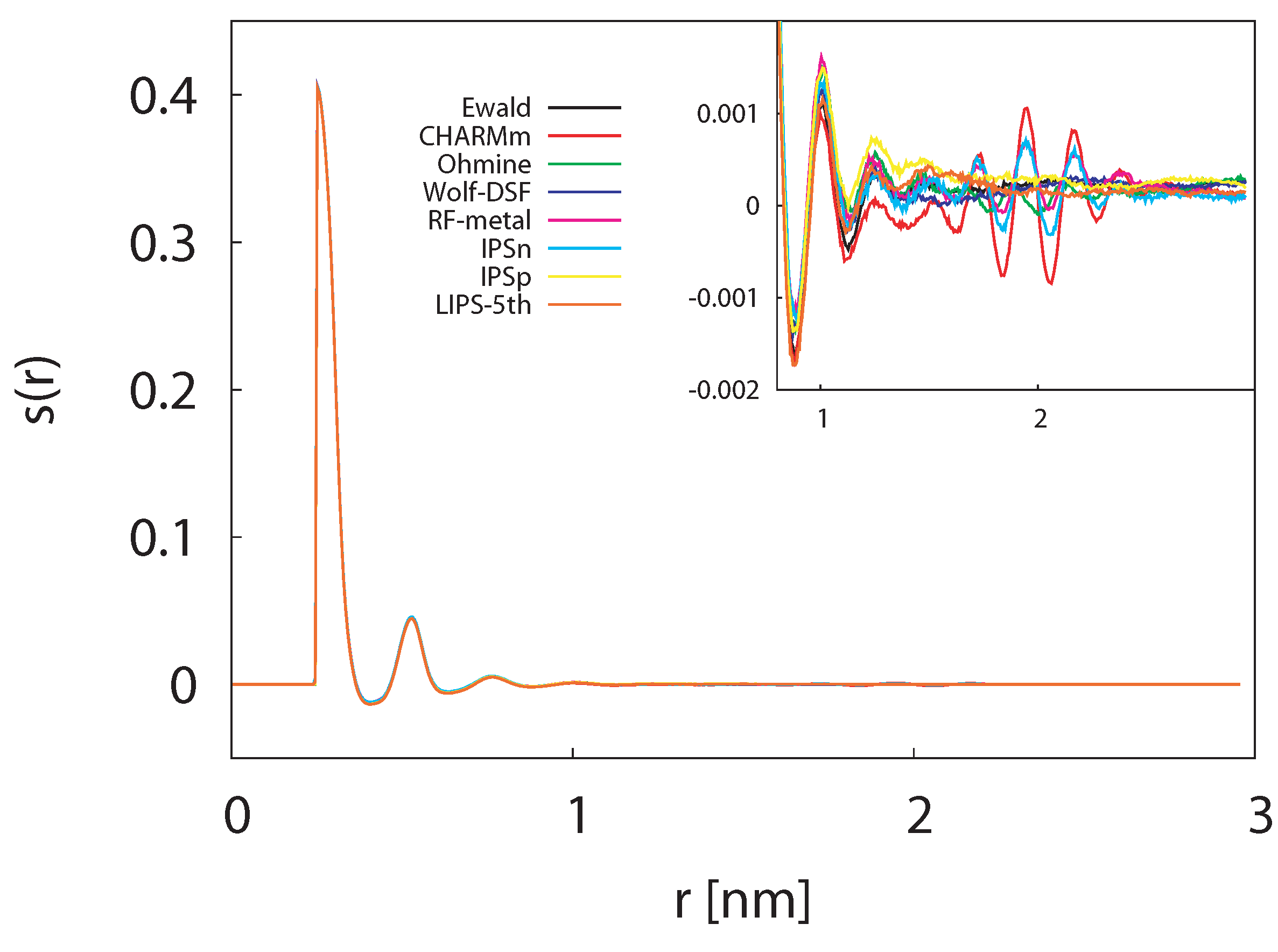
4. Conclusions
Acknowledgments
Conflict of Interest
References
- Ewald, P. The calculation of optical and electrostatic grid potential. Ann. Phys. 1921, 64, 253–287. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N log (N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.; Darden, T.; Lee, H.; Pedersen, L. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Yokota, R.; Barba, L.A.; Narumi, T.; Yasuoka, K. Petascale turbulence simulation using a highly parallel fast multipole method on GPUs. Comput. Phys. Commun. 2012, 184, 445–455. [Google Scholar] [CrossRef]
- Roberts, J.; Schnitker, J. How the unit cell surface charge distribution affects the energetics of ion–solvent interactions in simulations. J. Chem. Phys. 1994, 101, 5024–5031. [Google Scholar] [CrossRef]
- Roberts, J.; Schnitker, J. Boundary conditions in simulations of aqueous ionic solutions: A systematic study. J. Chem. Phys. 1995, 99, 1322–1331. [Google Scholar] [CrossRef]
- Luty, B.; van Gunsteren, W. Calculating electrostatic interactions using the particle-particle particle-mesh method with nonperiodic long-range interactions. J. Chem. Phys. 1996, 100, 2581–2587. [Google Scholar] [CrossRef]
- Hünenberger, P.; McCammon, J. Ewald artifacts in computer simulations of ionic solvation and ion–ion interaction: A continuum electrostatics study. J. Chem. Phys. 1999, 110, 1856–1873. [Google Scholar] [CrossRef]
- Hünenberger, P.; McCammon, J. Effect of artificial periodicity in simulations of biomolecules under Ewald boundary conditions: A continuum electrostatics study. Biophys. Chem. 1999, 78, 69–88. [Google Scholar] [CrossRef]
- Weber, W.; Hünenberger, P.; McCammon, J. Molecular dynamics simulations of a polyalanine octapeptide under Ewald boundary conditions: Influence of artificial periodicity on peptide conformation. J. Phys. Chem. B 2000, 104, 3668–3675. [Google Scholar] [CrossRef]
- Patra, M.; Karttunen, M.; Hyvönen, M.; Falck, E.; Vattulainen, I. Lipid bilayers driven to a wrong lane in molecular dynamics simulations by subtle changes in long-range electrostatic interactions. J. Phys. Chem. B 2004, 108, 4485–4494. [Google Scholar] [CrossRef]
- Beck, D.; Armen, R.; Daggett, V. Cutoff size need not strongly influence molecular dynamics results for solvated polypeptides. Biochemistry 2005, 44, 609–616. [Google Scholar] [CrossRef] [PubMed]
- Monticelli, L.; Simões, C.; Belvisi, L.; Colombo, G. Assessing the influence of electrostatic schemes on molecular dynamics simulations of secondary structure forming peptides. J. Phys. Condens. Matter 2006. [Google Scholar] [CrossRef]
- Reif, M.; KraÌĹutler, V.; Kastenholz, M.; Daura, X.; HuÌĹnenberger, P. Molecular dynamics simulations of a reversibly folding β-heptapeptide in methanol: Influence of the treatment of long-range electrostatic interactions. J. Phys. Chem. B 2009, 113, 3112–3128. [Google Scholar] [CrossRef] [PubMed]
- Linse, P.; Andersen, H.C. Truncation of Coulombic interactions in computer simulations of liquids. J. Chem. Phys. 1986, 85, 3027–3041. [Google Scholar] [CrossRef]
- Hoheisel, C. Bulk viscosity of model fluids. A comparison of equilibrium and nonequilibrium molecular dynamics results. J. Chem. Phys. 1987, 86, 2328–2334. [Google Scholar] [CrossRef]
- Hoheisel, C.; Vogelsang, R.; Schoen, M. Bulk viscosity of the Lennard-Jones fluid for a wide range of states computed by equilibrium molecular dynamics. J. Chem. Phys. 1987, 87, 7195–7198. [Google Scholar] [CrossRef]
- Smit, B. Phase diagrams of Lennard-Jones fluids. J. Chem. Phys. 1992, 96, 8639–8640. [Google Scholar] [CrossRef]
- Trokhymchuk, A.; Alejandre, J. Computer simulations of liquid/vapor interface in Lennard-Jones fluids: Some questions and answers. J. Chem. Phys. 1999, 111, 8510–8524. [Google Scholar] [CrossRef]
- Lopez-Lemus, J.; Alejandre, J. Thermodynamic and transport properties of simple fluids using lattice sums: Bulk phases and liquid-vapour interface. Mol. Phys. 2002, 100, 2983–2992. [Google Scholar] [CrossRef]
- Neumann, M.; Steinhauser, O. The influence of boundary conditions used in machine simulations on the structure of polar systems. Mol. Phys. 1980, 39, 437–454. [Google Scholar] [CrossRef]
- Alper, H.; Levy, R. Computer simulations of the dielectric properties of water: Studies of the simple point charge and transferrable intermolecular potential models. J. Chem. Phys. 1989, 91, 1242–1251. [Google Scholar] [CrossRef]
- Kitchen, D.; Hirata, F.; Westbrook, J.; Levy, R.; Kofke, D.; Yarmush, M. Conserving energy during molecular dynamics simulations of water, proteins, and proteins in water. J. Comput. Chem. 1990, 11, 1169–1180. [Google Scholar] [CrossRef]
- Tasaki, K.; McDonald, S.; Brady, J. Observations concerning the treatment of long-range interactions in molecular dynamics simulations. J. Comput. Chem. 1993, 14, 278–284. [Google Scholar] [CrossRef]
- Smith, P.; van Gunsteren, W. Consistent dielectric properties of the simple point charge and extended simple point charge water models at 277 and 300 K. J. Chem. Phys. 1994, 100, 3169–3175. [Google Scholar] [CrossRef]
- Feller, S.; Pastor, R.; Rojnuckarin, A.; Bogusz, S.; Brooks, B. Effect of electrostatic force truncation on interfacial and transport properties of water. J. Phys. Chem. 1996, 100, 17011–17020. [Google Scholar] [CrossRef]
- Van der Spoel, D.; van Maaren, P.; Berendsen, H. A systematic study of water models for molecular simulation: Derivation of water models optimized for use with a reaction field. J. Chem. Phys. 1998, 108, 10220–10231. [Google Scholar] [CrossRef]
- Mark, P.; Nilsson, L. Structure and dynamics of liquid water with different long-range interaction truncation and temperature control methods in molecular dynamics simulations. J. Comput. Chem. 2002, 23, 1211–1219. [Google Scholar] [CrossRef] [PubMed]
- Yonetani, Y. A severe artifact in simulation of liquid water using a long cut-off length: Appearance of a strange layer structure. Chem. Phys. Lett. 2005, 406, 49–53. [Google Scholar] [CrossRef]
- Van der Spoel, D.; van Maaren, P. The origin of layer structure artifacts in simulations of liquid water. J. Chem. Theory Comput. 2006, 2, 1–11. [Google Scholar] [CrossRef]
- Yonetani, Y. Liquid water simulation: A critical examination of cutoff length. J. Chem. Phys. 2006, 124, 204501–204512. [Google Scholar] [CrossRef] [PubMed]
- Loncharich, R.; Brooks, B. The effects of truncating long-range forces on protein dynamics. Proteins Struct. Funct. Bioinform. 1989, 6, 32–45. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, H.; Steinhauser, O. Cutoff size does strongly influence molecular dynamics results on solvated polypeptides. Biochemistry 1992, 31, 5856–5860. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, H.; Steinhauser, O. Molecular dynamics studies of solvated polypeptides: Why the cut-off scheme does not work. Chem. Phys. 1992, 168, 75–89. [Google Scholar] [CrossRef]
- Schreiber, H.; Steinhauser, O. Taming cut-off induced artifacts in molecular dynamics studies of solvated polypeptides. The reaction field method. J. Mol. Biol. 1992, 228, 909–923. [Google Scholar] [CrossRef]
- Saito, M. Molecular dynamics simulations of proteins in water without the truncation of long-range Coulomb interactions. Mol. Simul. 1992, 8, 321–333. [Google Scholar] [CrossRef]
- Guenot, J.; Kollman, P. Conformational and energetic effects of truncating nonbonded interactions in an aqueous protein dynamics simulation. J. Comput. Chem. 1993, 14, 295–311. [Google Scholar] [CrossRef]
- Saito, M. Molecular dynamics simulations of proteins in solution: Artifacts caused by the cutoff approximation. J. Chem. Phys. 1994, 101, 4055–4062. [Google Scholar] [CrossRef]
- Oda, K.; Miyagawa, H.; Kitamura, K. How does the electrostatic force cut-off generate non-uniform temperature distributions in proteins? Mol. Simul. 1996, 16, 167–177. [Google Scholar] [CrossRef]
- Norberg, J.; Nilsson, L. On the truncation of long-range electrostatic interactions in DNA. Biophys. J. 2000, 79, 1537–1553. [Google Scholar] [CrossRef]
- Patra, M.; Karttunen, M.; Hyvönen, M.; Falck, E.; Lindqvist, P.; Vattulainen, I. Molecular dynamics simulations of lipid bilayers: Major artifacts due to truncating electrostatic interactions. Biophys. J. 2003, 84, 3636–3645. [Google Scholar] [CrossRef]
- Mazars, M. Long ranged interactions in computer simulations and for quasi-2D systems. Phys. Rep. 2011, 500, 43–116. [Google Scholar] [CrossRef]
- Piana, S.; Lindorff-Larsen, K.; Dirks, R.M.; Salmon, J.K.; Dror, R.O.; Shaw, D.E. Evaluating the effects of cutoffs and treatment of long-range electrostatics in protein folding simulations. PLoS One 2012, 7, e39918. [Google Scholar] [CrossRef] [PubMed]
- Wolf, D.; Keblinski, P.; Phillpot, S.; Eggebrecht, J. Exact method for the simulation of Coulombic systems by spherically truncated, pairwise r summation. J. Chem. Phys. 1999, 110, 8254–8283. [Google Scholar] [CrossRef]
- Fennell, C.J.; Gezelter, J.D. Is the Ewald summation still necessary? Pairwise alternatives to the accepted standard for long-range electrostatics. J. Chem. Phys. 2006, 124, e234104. [Google Scholar] [CrossRef] [PubMed]
- Mendoza, F.; López-Lemus, J.; Chapela, G.; Alejandre, J. The wolf method applied to the liquid-vapor interface of water. J. Chem. Phys. 2008, 129, e024706. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, K.Z.; Narumi, T.; Yasuoka, K. Cutoff radius effect of the isotropic periodic sum and Wolf method in liquid-vapor interfaces of water. J. Chem. Phys. 2011, 134, e174112. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Brooks, B. Isotropic periodic sum: A method for the calculation of long-range interactions. J. Chem. Phys. 2005, 122, e44107. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Brooks, B. Using the isotropic periodic sum method to calculate long-range interactions of heterogeneous systems. J. Chem. Phys. 2008, 129, e154115. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Brooks, B. Isotropic periodic sum of electrostatic interactions for polar systems. J. Chem. Phys. 2009, 131, e024107. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, K.; Yasuoka, K.; Narumi, T. Cutoff radius effect of isotropic periodic sum method for transport coefficients of Lennard-Jones liquid. J. Chem. Phys. 2007, 127, e114511. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, K.; Narumi, T.; Yasuoka, K. Cutoff radius effect of the isotropic periodic sum method in homogeneous system. II. Water. J. Chem. Phys. 2010, 133, e014109. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, K.; Narumi, T.; Yasuoka, K. Cut-off radius effect of the isotropic periodic sum method for polar molecules in a bulk water system. Mol. Simul. 2012, 38, 397–403. [Google Scholar] [CrossRef]
- Kameoka, S.; Takahashi, K.Z.; Nozawa, T.; Narumi, T.; Yasuoka, K. Application of isotropic periodic sum method for macromolecular systems. I. 4-pentyl-4’-cyanobiphenyl liquid crystal. 2013; submitted. [Google Scholar]
- Klauda, J.; Wu, X.; Pastor, R.; Brooks, B. Long-range Lennard-Jones and electrostatic interactions in interfaces: Application of the isotropic periodic sum method. J. Chem. Phys. B 2007, 111, 4393–4400. [Google Scholar] [CrossRef] [PubMed]
- Venable, R.; Chen, L.; Pastor, R. Comparison of the extended isotropic periodic sum and particle mesh ewald methods for simulations of lipid bilayers and monolayers. J. Chem. Phys. B 2009, 113, 5855–5862. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, H.; Ohto, T.; Nagata, Y. Polarizable site charge model at liquid/solid interfaces for describing surface polarity: Application to structure and molecular dynamics of water/rutile TiO2 (110) interface. J. Chem. Theory Comput. 2013, 9, 1193–1201. [Google Scholar] [CrossRef]
- Takahashi, K.Z.; Narumi, T.; Yasuoka, K. A combination of the tree-code and IPS method to simulate large scale systems by molecular dynamics. J. Chem. Phys. 2011, 135, e174108. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, K.Z.; Narumi, T.; Suh, D.; Yasuoka, K. An improved isotropic periodic sum method using linear combinations of basis potentials. J. Chem. Theory Comput. 2012, 8, 4503–4516. [Google Scholar] [CrossRef]
- Takahashi, K.Z. Design of a reaction field using a linear-combination-based isotropic periodic sum method. J. Chem. Phys. 2013. submitted. [Google Scholar] [CrossRef] [PubMed]
- Brooks, B.R.; Bruccoleri, R.E.; Olafson, B.D.; States, D.J.; Swaminathan, S.; Karplus, M. CHARMM: A program for macromolecular energy, minimization and dynamic calculations. J. Comput. Chem. 1983, 4, 187–217. [Google Scholar] [CrossRef]
- Matsumoto, M.; Saito, S.; Ohmine, I. Molecular dynamics simulation of the ice nucleation and growth process leading to water freezing. Nature 2002, 416, 409–413. [Google Scholar] [CrossRef] [PubMed]
- Berendsen, H.; Grigera, J.; Straatsma, T. The missing term in effective pair potentials. J. Phys. Chem. 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Swope, W.; Andersen, H.; Berens, P.; Wilson, K. A computer simulation method for the calculation of equilibrium constants for the formation of physical clusters of molecules: Application to small water clusters. J. Phys. Chem. 1982, 76, 637–650. [Google Scholar] [CrossRef]
- Andersen, H. Rattle: A “velocity" version of the shake algorithm for molecular dynamics calculations. J. Comput. Phys. 1983, 52, 24–34. [Google Scholar] [CrossRef]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–520. [Google Scholar] [CrossRef]
- Hoover, W. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [PubMed]
© 2013 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Takahashi, K.Z. Truncation Effects of Shift Function Methods in Bulk Water Systems. Entropy 2013, 15, 3249-3264. https://doi.org/10.3390/e15083339
Takahashi KZ. Truncation Effects of Shift Function Methods in Bulk Water Systems. Entropy. 2013; 15(8):3249-3264. https://doi.org/10.3390/e15083339
Chicago/Turabian StyleTakahashi, Kazuaki Z. 2013. "Truncation Effects of Shift Function Methods in Bulk Water Systems" Entropy 15, no. 8: 3249-3264. https://doi.org/10.3390/e15083339



