Optimal Forgery and Suppression of Ratings for Privacy Enhancement in Recommendation Systems
Abstract
: Recommendation systems are information-filtering systems that tailor information to users on the basis of knowledge about their preferences. The ability of these systems to profile users is what enables such intelligent functionality, but at the same time, it is the source of serious privacy concerns. In this paper we investigate a privacy-enhancing technology that aims at hindering an attacker in its efforts to accurately profile users based on the items they rate. Our approach capitalizes on the combination of two perturbative mechanisms—the forgery and the suppression of ratings. While this technique enhances user privacy to a certain extent, it inevitably comes at the cost of a loss in data utility, namely a degradation of the recommendation’s accuracy. In short, it poses a trade-off between privacy and utility. The theoretical analysis of such trade-off is the object of this work. We measure privacy as the Kullback-Leibler divergence between the user’s and the population’s item distributions, and quantify utility as the proportion of ratings users consent to forge and eliminate. Equipped with these quantitative measures, we find a closed-form solution to the problem of optimal forgery and suppression of ratings, an optimization problem that includes, as a particular case, the maximization of the entropy of the perturbed profile. We characterize the optimal trade-off surface among privacy, forgery rate and suppression rate, and experimentally evaluate how our approach could contribute to privacy protection in a real-world recommendation system.1. Introduction
From the advent of the Internet and the World Wide Web, the amount of information available to users has grown exponentially. As a result, the ability to find information relevant for their interests has become a central issue in recent years. In this context of information overload, recommendation systems arise to provide information tailored to users on the basis of knowledge about their preferences [2]. In essence, a recommendation system may be regarded as a type of information-filtering system that suggests information items users may be interested in. Examples of such systems include recommending music at Last.fm and Pandora Radio, movies by MovieLens and Netflix, videos at YouTube, news at Digg and Google News, and books and other products at Amazon.
Most of these systems capitalize on the creation of profiles that represent interests and preferences of users. Such profiles are the result of the collection and analysis of the data that users communicate to those systems. A distinction is frequently made between explicit and implicit forms of data collection. The most popular form of explicit data collection is that users communicate their preferences by rating items. This is the case of many of the applications mentioned above, where users assign ratings to songs, movies or news they have already listened, watched or read. Other strategies to capture users’ interests include asking them to sort a number of items by order of predilection, or suggesting that they mark the items they like. On the other hand, recommendation systems may collect data from users without requiring them to explicitly convey their preferences [3]. These practices comprise observing the items clicked by users in an online store, analyzing the time it takes users to examine an item, or simply keeping a record of the purchased items.
The prolonged collection of these personal data allows the system to extract an accurate snapshot of user interests, i.e., their profiles. With this invaluable source of information, the recommendation system applies some technique [4] to generate a prediction of users’ interests for those items they have not yet considered. For example, Movielens and Digg use collaborative-filtering techniques [5] to predict the rating that a user would give to a movie and to create a personalized list of recommended news, respectively. In a nutshell, the ability of profiling users based on such personal information is precisely what enables the intelligent functionality of those systems.
Despite the many advantages recommendation systems are bringing to users, the information collected, processed and stored by these systems prompts serious privacy concerns. One of the main privacy risks perceived by users is that of a computer “figuring things out” about them [6]. Many users are worried about the idea that their profiles may reveal sensitive information such as health-related issues, political preferences, salary or religion. Such privacy risk is exacerbated especially when these profiles are combined across several information services or enriched with data from social networks. An illustrative example is [7], which demonstrates that it is possible to unveil sensitive information about a person from their movie rating history by cross-referencing data from other sources. The authors analyzed the Netflix Prize data set [8], which contained anonymous movie ratings of around half a million users of Netflix, and were able to uncover the identity, political leaning and even sexual orientation of some of those users, by simply correlating their ratings with reviews they posted on the popular movie Web site IMDb. Apart from the risk of cross-referencing, users are also concerned that the system’s predictions may be totally erroneous and be later used to defame them. This latter situation is examined in [9], where the accuracy of the predictions provided by TiVo digital video recorder and Amazon is questioned. Lastly, other privacy risks embrace unsolicited marketing, information leaked to other users of the same computer, court subpoenas, and government surveillance [6].
Some of the privacy risks described above arise from a lack of confidence in recommendation systems. Knowing how users’ data are treated and protected would certainly help engender trust. However, even in those cases where users could completely trust a recommendation system, such system could also be subject to security breaches resulting in theft or disclosure of sensitive information. Some examples include Sony’s security breach [10] and Evernote’s [11]. So whether privacy is preserved or not depends not only on the trustworthiness of the data controller but also on its capacity to effectively manage the entrusted data.
Systems like Amazon or Delicious protect users’ data during transmission by using secure sockets layer software, which in essence encrypts the information users submit. However, beyond this, most recommendation systems do not specify which security measures are adopted once those data have been collected. Encrypting those data and using numbers instead of names might be a common strategy to give their users anonymity. However, this strategy may not always be effective. AOL user No. 4417749 found this out the hard way in 2006, when AOL released a text file intended for research purposes containing twenty million search keywords including hers. Reporters were able to narrow down the 62-year-old widow in Lilburn, Ga., by examining the content of her search queries [12].
On the other hand, systems such as Last.fm and Movielens claim to use firewalls and to store users’ data on terminals which require password access. However, as these systems know such level of protection may be insufficient, they explicitly claim that those measures could not stop an attacker from “getting around the privacy or security settings on the Web site through unforeseen and/or illegal activity” [13]. In the unlikely event of an absolutely secure recommendation system, we must also bear in mind that the system could be legally enforced to reveal the information they have access to. In 2008, for example, as part of a copyright infringement lawsuit against YouTube, a US judge ordered the popular online video-sharing service to hand over a database linking users with every video clip they had watched [14].
As a result of all these privacy and security concerns, it is therefore not surprising that some users are reticent to reveal their interests. In fact, [15] reports that the 24% of Internet users surveyed provided false information in order to avoid giving private information to a Web site. Alternatively, another study [16] finds that 95% of the respondents refused, at some point, to provide personal information when requested by aWeb site. In closing, these studies seem to indicate that submitting false information and refusing to give private information are strategies accepted by users concerned with their privacy.
1.1. Contribution and Plan of this Paper
In this paper, we approach the problem of protecting user privacy in those recommendation systems that profile users on the basis of the items they rate. Our set of potential privacy attackers comprises any entity who may ascertain the interests of users from their ratings. Obviously, this set includes the recommender itself, but also the network operator and any passive eavesdropper.
Given the willingness of users to provide fake information and elude disclosing private data, we investigate a privacy-enhancing technology (PET) that combines these two forms of data perturbation, namely, the forgery and the suppression of ratings. Concordantly, in our scenario users rate those items they have an opinion on. However, in order to avoid being accurately profiled by an attacker, users may wish to refrain from rating some of those items and/or rate items that do not reflect their actual preferences. Our approach thus protects user privacy to a certain degree, without having to trust the recommendation system or the network operator, but at the cost of a loss in utility, a degradation of the quality of the recommendation. In other words, our PET poses a trade-off between privacy and utility.
The theoretical analysis of the trade-off between these two contrasting aspects is the object of this work. We tackle the issue in a systematic fashion, drawing upon the methodology of multiobjective optimization. Before proceeding, though, we adopt a quantifiable measure of user privacy—the Kullback-Leibler (KL) divergence or relative entropy between the probability distribution of the user’s items and the population’s distribution, a criterion that we justified and interpreted in previous work [17,18] by leveraging on the rationale behind entropy-maximization methods. Equipped with a measure of both privacy and utility, we formulate an optimization problem modeling the trade-off between privacy on the one hand, and on the other forgery rate and suppression rate as utility metrics. The proposed formulation contemplates, as a special case, the maximization of the entropy of the user’s perturbed profile. Our theoretical analysis finds a closed-form solution to the problem of optimal forgery and suppression of ratings, and characterizes the optimal trade-off between the aspects of privacy and utility.
In addition, we provide an empirical evaluation of our data-perturbative approach. Specifically, we apply the forgery and the suppression of ratings in the popular movie recommendation system Movielens, and show how these two strategies may preserve the privacy of its users.
Section 2 reviews several data-perturbative approaches aimed at enhancing user privacy in the context of recommender systems. Section 3 introduces our privacy-enhancing technology, proposes a quantitative measure of the privacy of user profiles, and formulates the trade-off between privacy and utility. Section 4 presents a theoretical analysis of the optimization problem characterizing the privacy-forgery-suppression trade-off. In this same section we also provide a numerical example that illustrates our formulation and theoretical results. Section 5 evaluates our privacy-protecting mechanism in a real recommendation system. Conclusions are drawn in Section 6. Finally, Appendices A–D provide the proofs of the results included in Section 4.
2. State of the Art
Numerous approaches have been proposed to protect user privacy in the context of recommendation systems. These approaches fundamentally suggest either perturbing the information provided by users or using cryptographic techniques.
In the case of perturbative methods for recommendation systems, [19] proposes that users add random values to their ratings and then submit these perturbed ratings to the recommender. After receiving these ratings, the system executes an algorithm and sends the users some information that allows them to compute the prediction. When the number of participating users is sufficiently large, the authors find that user privacy is protected to a certain extent and the system reaches a decent level of accuracy. However, even though a user disguises all their ratings, it is evident that the items themselves may uncover sensitive information. Simply put, the mere fact of showing interest in a certain item may be more revealing than the rating assigned to that item. For instance, a user rating a book called “How to Overcome Depression” indicates a clear interest in depression, regardless of the score assigned to this book. Apart from this critique, other works [20,21] stress that the use of randomized data distortion techniques might not be able to preserve privacy.
The authors of [19] propose in [22] the same data-perturbative technique but applied to collaborative-filtering algorithms based on singular-value decomposition. An important difference between both works is that the null entries, i.e., those items the user has not rated, are now replaced with the mean value of their ratings. In addition, the authors measure the level of privacy achieved by using the metric proposed in [23], which is essentially equivalent to differential entropy. Experimental results in Movielens and Jester show the trade-off curve between accuracy in recommendations and privacy. In particular, they assess accuracy as the mean absolute error between the predicted values from the original ratings and the predictions obtained from the perturbed ratings.
Although this latter approach prevents the recommendation system from learning about which items a user has rated and which not, it still suffers from a variety of drawbacks that limit its adoption. One of these limitations is that both [19,22] require the server to cooperate and participate in the execution of a protocol. But it is the user who is interested in their own privacy. The motivation for the system may be dubious, especially because privacy protection comes at the cost of a degradation of the quality of its recommendation algorithm. Besides, it is the recommendation system who decides how users will perturb their ratings. In particular, the system first chooses whether the random values to be added to the user’s ratings will be distributed according to either a uniform distribution or a Gaussian distribution; and then, the parameters of the distribution chosen are communicated to all users. Simply put, users do not decide to which extent their ratings will be altered, and cannot specify the level of privacy they wish to achieve with such perturbation. All this depends on the recommendation system.
As we shall see in the coming sections, our privacy-enhancing mechanism differs significantly from these two rating-perturbative schemes. Specifically, the proposed PET does not require infrastructure, it allows each user to configure the point of operation of the mechanism within the optimal privacy-utility trade-off surface, in the sense of maximizing privacy for a desired utility, or vice versa; it contemplates not only the submission of false ratings, but also the possibility of eliminating genuine data; and last but not least, far from being mutually exclusive, our PET may be combined synergically with other approaches based on user collaboration [24–26], anonymizers or pseudonymizers.
At this point, we would like to remark that the use of perturbative techniques is by no means new in other scenarios such as private information retrieval and the semantic Web. In the former scenario, users send general-purpose queries to an information service provider. A perturbative approach to protect user profiles in this context consists in combining genuine with false queries. Precisely, [27] proposes a nonrandomized method for query forgery and investigates the trade-off between privacy and the additional traffic overhead. In the semantic Web scenario, users annotate resources with the purpose of classifying them. In this application domain, the perturbation of user profiles for privacy preservation may be carried out by dropping certain annotations or tags. An example of this kind of perturbation may be found in [28–30], where the authors propose the elimination of tags as a privacy-enhancing strategy.
Regarding the use of cryptographic techniques, [31,32] propose a method that enables a community of users to calculate a public aggregate of their profiles without revealing them on an individual basis. In particular, the authors use a homomorphic encryption scheme and a peer-to-peer communication protocol for the recommender to perform this calculation. Once the aggregated profile is computed, the system sends it to users, who finally use local computation to obtain personalized recommendations. This proposal prevents the system or any external attacker from ascertaining the individual user profiles. However, its main handicap is assuming that an acceptable number of users is online and willing to participate in the protocol. In line with this, [33] uses a variant of Pailliers’ homomorphic cryptosystem which improves the efficiency in the communication protocol. Another solution [34] presents an algorithm aimed at providing more efficiency by using the scalar product protocol.
3. Privacy Protection via Forgery and Suppression of Ratings
In this section, first we present the forgery and the suppression of ratings as a privacy-enhancing technology. The description of our approach is prefaced by a brief introduction of the concepts of soft privacy and hard privacy. Secondly, we propose a model of user profile and set forth our assumptions about the adversary capabilities. Finally, we provide a quantitative measure of both privacy and utility, and present a formulation of the trade-off between these two contrasting aspects.
3.1. Soft Privacy vs. Hard Privacy
The privacy research literature [35] recognizes the distinction between the concepts of soft privacy and hard privacy. A privacy-enhancing mechanism providing soft privacy assumes that users entrust their private data to an entity, which is thereafter responsible for the protection of their data. In the literature, numerous attempts to protect privacy have followed the traditional method of anonymous communications [36–45], which is fundamentally based on the suppositions of soft privacy. Unfortunately, anonymous-communication systems are not completely effective [46–49], they normally come at the cost of infrastructure, and assume that users are willing to trust other parties (a).
Our privacy-protecting technique, per contra, leverages on the principle of hard privacy, which assumes that users mistrust communicating entities and therefore strive to reveal as little private information as possible. In the motivating scenario of this work, hard privacy means that users need not trust an external entity such as the recommender or the network operator. Consequently, because users just trust themselves, it is their own responsibility to protect their privacy. In this state of affairs, the forgery and the suppression of ratings appear as a technique that may hinder privacy attackers in their efforts to accurately profile users on the basis of the items they rate. Specifically, when users are adhered to this technique, they have the possibility to submit ratings to items that do not reflect their genuine preferences, and/or refrain from rating some items of their interest—this is what we refer to as the forgery and the suppression of ratings, respectively.
3.2. User Profile and Adversary Model
In the scenario of recommendation systems, users rate items of a very different nature, e.g., music, pictures, videos or news, according to their personal preferences. The information conveyed allows those systems to extract a profile of interests or user profile, which turns to be essential in the provision of personalized recommendations.
We mentioned in Section 1 that Movielens represents user profiles by using some kind of histogram. Other systems such as Jinni and Last.fm show this information by means of a tag cloud, which in essence may be regarded as another kind of histogram. In this same spirit, recent privacy-protecting approaches in the scenario of recommendation systems also propose using histograms of absolute frequencies for modeling user profiles [51,52].
According to these examples and inspired by other works in the field [1,28–30,53,54], we model the items rated by users as random variables (r.v.’s) taking on values in a common finite alphabet of categories, namely the set {1, . . . , n} for some integer n ≥ 2. Concordantly, we model the profile of a user as a probability mass function (PMF) q = (q1, . . . , qn), that is, a histogram of relative frequencies of items within a predefined set of categories of interest.
Although for simplicity our user-profile model captures only the items rated by users, we would like to remark that this same model could also include information of implicit nature. In other words, our user-profile model could very well be applied to those recommendation systems which collect not only the ratings explicitly conveyed by users, but also the Web pages they explore, the time it takes them to examine those pages or the items purchased. Examples of such systems include Amazon and Google News.
We would also like to emphasize that, under our user-profile model based on explicit ratings, profiles do not capture the particular scores given to items, but what we consider to be more sensitive: the categories these items belong to. This is exactly the case of Movielens and numerous content-based recommendation systems. Figure 1 provides an example that illustrates how user profiles are constructed in Movielens. In this particular example, a user assigns two stars to a movie, meaning that they consider it to be “fairly bad”. However, the recommender updates their profile based only on the categories this movie belongs to.
According to this model, a privacy attacker supposedly observes a perturbed version of this profile, resulting from the forgery and the suppression of certain ratings, and is unaware or ignores the fact that the observed user profile, also in the form of a histogram, does not reflect the actual profile of interests of the user in question. In principle, our passive attacker could be the recommender itself or the network operator. However, the set of potential attackers is not restricted merely to these two entities. Since ratings are often publicly available to other users of the recommendation system, any other attacker able to crawl through this information is taken into consideration in our adversary model.
When users adhere to the forgery and the suppression of ratings, they specify a forgery rate ρ isin; [0,∞) and a suppression rate σ isin; [0, 1). The former is the ratio of forged ratings to total genuine ratings that a user consents to submit. The latter ratio is the fraction of genuine ratings that the user agrees to eliminate (b). Note that, in our approach, the number of false ratings submitted by the user can exceed the number of genuine ratings, that is, ρ can be greater than 1. Nevertheless, the number of suppressed ratings is always lower than the number of genuine ratings.
By forging and suppressing ratings, the actual profile of interests q is then perceived from the outside as the apparent PMF , according to a forgery strategy r = (r1, . . . , rn) and a suppression strategy s = (s1, . . . , sn). Such strategies represent the proportion of ratings that the user should forge and eliminate in each of the n categories. Naturally, these strategies must satisfy, on the one hand, that ri ≥ 0, si ≥ 0 and qi +ri −si ≥ 0 for i = 1, . . . , n, and on the other, that and . In conclusion, the apparent profile is the result of the addition and the substraction of certain items to/from the actual profile, and the posterior normalization by so that .
3.3. Measuring the Privacy of User Profiles
Inspired by the privacy measures proposed in [17,27,28,55], and according to the model of user profile assumed in Section 3.2, we define initial privacy risk as the KL divergence [56] between the user’s genuine profile and the population’s distribution, that is,
Similarly, we define (final) privacy risk as the KL divergence between the user’s apparent profile and the population’s distribution,
In our attempt to quantify privacy risk, we have therefore assumed that the user knows, or is able to estimate, the distribution p representing the average interest. We consider this is a reasonable assumption, in part because many recommendation systems provide the categories their items belong to as well as detailed statistics about the ratings assigned by users. If this information were not enough to build the population’s profile, users could alternatively resort to databases containing this kind of data. An example of such databases is Google AdWords Display Planner [57], which provides estimates of the number of times that ads, classified according to a predefined set of topics, are shown on a search result page or other site on the Google Display Network [58]. Since ads of this network are displayed based on the search queries submitted by users and the content of the Web pages browsed, those estimates provide a means to compute the population’s profile. Precisely, this is the methodology followed by [59,60] to estimate p.
Once we have defined our measure of privacy, next we proceed to justify it. An intuitive justification of our privacy metric stems from the observation that, whenever the user’s apparent item distribution diverges too much from the population’s, a privacy attacker will have actually gained some information about the user, in contrast to the statistics of the general population.
A richer interpretation arises from the fact that Shannon’s entropy may be regarded as a special case of KL divergence. Precisely, let u denote the uniform distribution on {1, . . . , n}, that is, ui = 1/n. In the special case when p = u, the privacy risk becomes
In other words, minimizing the KL divergence is equivalent to maximizing the entropy of the user’s apparent item distribution. Accordingly, instead of using the measure of privacy risk represented by the KL divergence, relative to the population’s distribution, we would use the entropy H(t) as an absolute measure of privacy gain.
This observation enables us to establish some riveting connections between Jaynes’ rationale on entropy-maximization methods and the use of entropies and divergences as measures of privacy. The leading idea is that the method of types from information theory establishes an approximate monotonic relationship between the likelihood of a PMF in a stochastic system and its Shannon’s entropy. Loosely speaking and in our context, the higher the entropy of a profile, the more likely it is, the more users behave similarly. This is in absence of a probability distribution model for the PMFs, viewed abstractly as r.v.’s themselves. Under this interpretation, Shannon’s entropy is a measure of anonymity, not in the sense that the user’s identity remains unknown, but only in the sense that higher likelihood of an apparent profile, believed by an external observer to be the actual profile, makes that profile more common, helping the user go unnoticed, less interesting to an attacker assumed to strive to target peculiar users.
If an aggregated histogram of the population were available as a reference profile, as we assume in this work, the extension of Jaynes’ argument to relative entropy also gives an acceptable measure of privacy (or anonymity). Recall [56] that KL divergence is a measure of discrepancy between probability distributions, which includes Shannon’s entropy as the special case when the reference distribution is uniform. Conceptually, a lower KL divergence hides discrepancies with respect to a reference profile, say the population’s, and there also exists a monotonic relationship between the likelihood of a distribution and its divergence with respect to the reference distribution of choice, which enables us to regard KL divergence as a measure of anonymity in a sense entirely analogous to the above mentioned.
Under this interpretation, the KL divergence is therefore interpreted as an (inverse) indicator of the commonness of similar profiles in said population. As such, we should hasten to stress that the KL divergence is a measure of anonymity rather than privacy, in the sense that the obfuscated information is the uniqueness of the profile behind the online activity, rather than the actual profile itself. Indeed, a profile of interests already matching the population’s would not require perturbation.
3.4. Formulation of the Trade-Off among Privacy, Forgery and Suppression
Our data-perturbative mechanism allows users to enhance their privacy to a certain extent, since the resulting profile, as observed from the outside, no longer captures their actual interests. The price to be paid, however, is a loss in data utility, in particular in the accuracy of the recommender’s predictions.
For the sake of tractability, in this work we consider as utility metrics the forgery rate and the suppression rate. This consideration enables us to formulate the problem of choosing a forgery strategy and a suppression strategy as a multiobjective optimization problem that takes into account privacy, forgery rate and suppression rate. Specifically, under the assumption that the population of users is large enough to neglect the impact of the choice of r and s on p, we define the privacy-forgery-suppression function
which characterizes the optimal trade-off among privacy, forgery rate and suppression rate.
Conceptually, the result of this optimization are two strategies r and s that contain information about which item categories should be forged and which ones should be suppressed, in order to achieve the minimum privacy risk. More precisely, the component ri is the percentage of items that the user should forge in the category i. The component si is defined analogously for suppression.
From a practical perspective, our rating-perturbative mechanism would be implemented as software installed on the user’s local machine, for example, in the form of a Web browser add-on. Specifically, building on the optimal forgery and the suppression strategies, the software implementation would advise the user when to refrain from rating a given item and when to submit false ratings to items that do not reflect their actual interests. For the sake of usability, the forgery and the suppression of ratings should in fact be completely transparent to the user. For this, the software could submit false ratings in an autonomous manner, without requiring the continuous supervision of the user. And the same could be done with suppression: users would be submitting genuine ratings while logged into the recommendation system, but the software could decide, at some point, not to forward some of those ratings. Further details on this can be found in [1], where we presented an architecture describing some practical implementation issues.
Last but not least, we would like to emphasize that the architecture proposed in the cited work could also be extended to recommendation systems relying on implicit feedback. To adapt this architecture to recommenders which profile users, for example, based on the pages they visit, the software could run processes in background that would browse the recommender’s site according to r. As for suppression, the proposed architecture could simply block access to the content suggested by s.
4. Optimal Forgery and Suppression of Ratings
This section is entirely devoted to the theoretical analysis of the privacy-forgery-suppression Function (4) defined in Section 3.4. In our attempt to characterize the trade-off among privacy risk, forgery rate and suppression rate, we shall present a closed-form solution to the optimization problem inherent in the definition of this function. Afterwards, we shall analyze some fundamental properties of said trade-off. For the sake of brevity, our theoretical analysis only contemplates the case when all given probabilities are strictly positive:
The general case can easily be dealt with, occasionally via continuity arguments, using the convention that and . Additionally, we suppose without loss of generality that
Before diving into the mathematical analysis, it is immediate from the definition of the privacy-forgery-suppression function that its initial value is (0, 0) = D(q || p). The characterization of the optimal trade-off surface modeled by (ρ, σ) at any other values of ρ and σ is the focus of this section.
4.1. Closed-Form Solution
Our first theorem, Theorem 3, will present a closed-form solution to the minimization problem involved in the definition of Function (4). The solution will be derived from Lemma 1, which addresses a resource allocation problem. This a theoretical problem encountered in many fields, from load distribution and production planning to communication networks, computer scheduling and portfolio selection [61]. Although this lemma provides a parametric-form solution, we shall be able to proceed towards an explicit closed-form solution, albeit piecewise.
Lemma 1 (Resource Allocation)
For all k = 1, . . . , n, let fk be a real-valued function on {(xk, yk) isin; ℝ2: κk + xk − yk ≥ 0}, twice differentiable in the interior of its domain. Assume that, that and that the Hessian H(fk) is positive semidefinite. Define. Because and, it follows that hk is strictly increasing in xk and strictly decreasing in yk. Consequently, for a fixed yk, hk(xk, yk) is an invertible function of xk. Denote by the inverse of hk(xk, 0). Suppose further that hk(xk, yk) = hk(xk − yk, 0) and finally that. Now consider the following optimization problem in the variables x1, . . . , xn and y1, . . . , yn:
- (i)
The solution to the problem ( ) depends on two real numbers ψ, ω that satisfy the equality constraints and. The solution exists provided that ψ ≤ ω. If ψ < ω, then the solution is unique and yields
If ψ = ω, then there exists an infinite number of solutions of the form ( ) for all αk isin; ℝ+ meeting the two aforementioned equality constraints.
Without loss of generality, suppose that h1(0, 0) ≤ ··· ≤ hn(0, 0).
- (ii)
For ψ < ω, consider the following cases:
- (a)
hi(0, 0) < ψ ≤ hi+1(0, 0) for some i = 1, . . . , j − 1 and hj−1(0, 0) ≤ ω < hj (0, 0) for some j = 2, . . . , n.
- (b)
hj−1(0, 0) ≤ ω for j = n+1 and, either hi(0, 0) < ψ ≤ hi+1(0, 0) for some i = 1, . . . , n−1 or hi(0, 0) < ψ for i = n.
- (c)
ψ ≤ hi+1(0, 0) for i = 0 and, either hj−1(0, 0) ≤ ω < hj (0, 0) for some j = 2, . . . , n or ω < hj (0, 0) for j = 1.
- (d)
hj−1(0, 0) ≤ ω for j = n + 1 and ψ ≤ hi+1(0, 0) for i = 0.
In each case, and for the corresponding indexes i and j,
- (iii)
For ψ = ω, consider the following cases:
- (a)
either hi(0, 0) < ψ < hj(0, 0) for some j = 2, . . . , n and i = j − 1, or hi(0, 0) < ψ = hi+1(0, 0) = ··· = hj−1(0, 0) < hj(0, 0) for some i = 1, . . . , j − 2 and some j = 3, . . . , n.
- (b)
for j = n+1, either hi(0, 0) < hi+1(0, 0) = ··· = hj−1(0, 0) = ω for some i = 1, . . . , j −2 or hj−1(0, 0) < ω with i = n.
- (c)
for i = 0, either ψ = hi+1(0, 0) = ··· = hj−1(0, 0) < hj(0, 0) for some j = 2, . . . , n or ψ < hi+1(0, 0) with j = 1.
In each case, and for the corresponding indexes i and j,
Proof
The proof is provided in Appendix A.
The previous lemma presented the solution to a resource allocation problem that minimizes a rather general but convex objective function, subject to affine constraints. Our next theorem, Theorem3, applies the results of this lemma to the special case of the objective function of problem (4). In doing so, we shall confirm the intuition that there must exist a set of ordered pairs (ρ, σ) where the privacy risk vanishes and another set where it does not. We shall refer to the former set as the critical-privacy region and formally define it as
The latter set will be the complementary set

Before proceeding with Theorem 3, first we shall introduce what we term forgery and suppression thresholds, two sequences of rates that will play a fundamental role in the characterization of the solution to the minimization problem defining the privacy-forgery-suppression function. Secondly, we shall investigate certain properties of these thresholds in Proposition 2. And thereafter, we shall introduce some definitions that will facilitate the exposition of the aforementioned theorem. Let and be the cumulative distribution functions corresponding to q and p. Denote by and the complementary cumulative distribution functions of q and p. Define the forgery thresholds ρi as
for j = 2, . . . , n. Additionally, define the suppression thresholds σj as
for j = 1, . . . , n, and σ0 = 1. Observe that ρ1 = σn = 0 and that the forgery threshold ρj is a linear function of σ. We shall refer to this latter threshold as the critical forgery-suppression threshold and denote it also by ρcrit(σ). The reason is that said threshold will determine the boundary of the critical-privacy region, as we shall see later. The following result, Proposition 2, characterizes the monotonicity of the forgery and the suppression thresholds.
Proposition 2 (Monotonicity of Thresholds)
- (i)
For j = 3, . . . , n and i = 1, . . . , j − 2, the forgery thresholds satisfy ρi ≤ ρi+1, with equality if, and only if,.
- (ii)
For j = 2, . . . , n, the suppression thresholds satisfy σj ≤ σj−1, with equality if, and only if,.
- (iii)
Further, for any j = 2, . . . , n and any σ isin; (σj, σj−1], the critical forgery-suppression threshold satisfies ρj(σ) ≥ ρj−1, with equality if, and only if, σ = σj−1.
Proof
The proof is presented in Appendix A.
Prior to investigate a closed-form solution to the problem (4), we introduce some definitions for ease of presentation. For i = 1, . . . , j − 1 and j = 2, . . . , n, define
where q̃ and p̃ are distributions in the probability simplex of j − i + 1 dimensions, and r̃ and s̃ are tuples of the same dimension that represent a forgery strategy and a suppression strategy, respectively. Particularly, note that the indexes i = 1 and j = n lead to q̃ = q and p̃ = p.
Theorem 3
Let ∂ 



- (i)
∂
⊂
and
- (ii)
For any (ρ, σ) isin; cl
, either ρ isin; [ρi, ρi+1] for i = 1 or ρ isin; (ρi, ρi+1] for some i = 2, . . . , j − 1, and either σ isin; [σj, σj−1] for j = n or σ isin; (σj, σj−1] for some j = 2, . . . , n − 1. Then, for the corresponding indexes i, j, the optimal forgery and suppression strategies are
and the corresponding, minimum KL divergence yields the privacy-forgery-suppression function
Proof
The proof is shown in Appendix A.
In light of this result, we would like to remark the intuitive principle that both the optimal forgery and suppression strategies follow. On the one hand, the forgery strategy suggests adding ratings to those categories with a low ratio , that is, to those in which the user’s interest is considerably lower than the population’s. On the other hand, the suppression strategy recommends eliminating ratings from those categories where the ratio is high, i.e., where the interest of the user exceeds that of the population.
Another straightforward consequence of Theorem 3 is the role of the forgery and the suppression thresholds. In particular, we identify ρi as the forgery rate beyond which the components of rk for k = 1, . . . , i become positive. A similar reasoning applies to σj, which indicates the suppression rate beyond which the components of sk for k = j, . . . , n are positive. In a nutshell, these thresholds determine the number of nonzero components of the optimal strategies.
Also, from this theorem we deduce that the perturbation of the user profile does not only affect those categories where either rk > 0 or sk > 0. In fact, since we are dealing with relative frequencies, the components of the apparent distribution tk belonging to the categories k = i + 1, . . . , j − 1 are normalized by . Figure 2 illustrates these three conclusions by means of a simple example with n = 5 categories of interest.
In this example we consider a user who is disposed to submit a percentage of false ratings ρ isin; (ρ2, ρ3], and to refrain from sending a fraction of genuine ratings σ isin; (σ4, σ3]. Given these rates, the optimal forgery strategy recommends that the user forge ratings belonging to the categories 1 and 2, where clearly there is a lack of interest, compared to the reference distribution. On the contrary, the suppression strategy specifies that the user eliminate ratings from the categories 4 and 5, that is, from those categories where they show too much interest, again compared to the population’s profile. In adopting these two strategies, the apparent user profile approaches the population’s distribution, especially in those components where the ratio deviates significantly from 1. Finally, the component of the apparent profile t3, which is not directly affected by the forgery and the suppression strategies, gets closer to p3 as a result of the aforementioned normalization.
In the following subsections, we shall analyze a number of important consequences of Theorem 3.
4.2. Orthogonality, Continuity and Proportionality
In this subsection we study some interesting properties of the closed-form solution obtained in Section 4.1. Specifically, we investigate the orthogonality and continuity of the optimal forgery and suppression strategies, and then establish a proportionality relationship between the optimal apparent user profile and the population’s distribution.
Corollary 4 (Orthogonality and Continuity)
- (i)
For any (ρ, σ) isin; cl
, the optimal forgery and suppression strategies satisfy for k = 1, . . . , n.
- (ii)
The components of r* and s*, interpreted as functions of ρ and σ respectively, are continuous on cl
.
Proof
The proof is provided in Appendix B.
The orthogonality of the optimal forgery and suppression strategies, in the sense indicated by Corollary 4 (i), conforms to intuition—it would not make any sense to submit false ratings to items of a particular category and, at the same time, eliminate genuine ratings from this category. This intuitive result is illustrated in Figure 2. The second part of this corollary is applied to show our next result, Proposition 5.
Proposition 5 (Proportionality)
Define the piecewise functions and on the intervals [σj, σj−1] for j = 2, . . . , n and [ρi, ρi+1] for i = 1, . . . , j − 1.
- (i)
For any j = 2, . . . , n and i = 1, . . . , j − 1, and for any σ isin; [σj, σj−1] and ρ isin; [ρi, ρi+1], the optimal apparent profile t* and the population’s distribution p satisfy
and
- (ii)
The function φ is continuous and strictly increasing in each of its arguments, and satisfies φ(ρ, σ) ≤ 1, with equality if, and only if, (ρ, σ) = (ρj(σ), σ).
- (iii)
The function χ is continuous and strictly decreasing in each of its arguments, and satisfies χ(ρ, σ) ≥ 1, with equality if, and only if, (ρ, σ) = (ρj(σ), σ).
Proof
The proof is presented in Appendix B.
Our previous result tells us how perturbation operates. According to Proposition 5, the optimal strategies perturb the user profile in such a manner that, in those categories with the lowest and highest ratios , the apparent profile becomes proportional to the population’s distribution. More precisely, the common ratio increases with both ρ and σ in those categories affected by forgery, that is, k = 1, . . . , i. Exactly the opposite happens in those categories affected by suppression, where the common ratio decreases with both rates. This tendency continues until ρ = ρcrit(σ), at which point t* = p. Figure 3 illustrates this proportionality property in the case of the example depicted in Figure 2.
4.3. Critical-Privacy Region
One of the results of Theorem 3 is that the boundary of the critical-privacy region is determined by the critical forgery-suppression threshold ρj(σ), which we also denote by ρcrit(σ) to highlight this fact. The following proposition leverages on this result and characterizes said region. In particular, Proposition 6 first examines some properties of this threshold and then investigates the convexity of the critical-privacy region.
Proposition 6 (Convexity of the Critical-Privacy Region)
- (i)
ρj is a convex, piecewise linear function of σ isin; [σj, σj−1] for j = 2, . . . , n.
- (ii)
is convex.
Proof
The proof is presented in Appendix C.
The conclusions drawn from this theoretical result are illustrated in Figure 4. In this figure we represent the critical and noncritical-privacy regions for n = 5 categories of interest; the distributions q and p assumed in this conceptual example are different from those considered in Figures 2 and 3. That said, the figure in question shows a straightforward consequence of our previous proposition—the noncritical-privacy region is nonconvex.
In this illustrative example, the sequences of forgery thresholds {ρ1 . . . , ρ5} and suppression thresholds {σ5, . . . , σ1} are strictly increasing. By Proposition 2, we can conclude then that the inequalities of the labeling assumption (6) hold strictly. Related to these thresholds is also the number of nonzero components of the optimal strategies, as follows from Theorem 3. Figure 4 shows the sets of pairs (ρ, σ) where the number of nonzero components of r* and s* is fixed. Thus, in the triangular area shown darker, corresponding to the Cartesian product of the intervals [ρ3, ρ4] and [σ4, σ3], the solutions r* and s* have i = 3 and n − j +1 = 2 nonzero components, respectively.
4.4. Case of Low Forgery and Suppression
This subsection characterizes the privacy-forgery-suppression function in the special case when ρ, σ ≃ 0.
Proposition 7 (Low Rates of Forgery and Suppression)
Assume the nontrivial case in which q ≠ p. Then, there exist two indexes i, j such that 0 = ρ1 = ··· = ρi < ρi+1 and 0 = σn = ··· = σj < σj−1. For any ρ isin; [0, ρi+1] and σ isin; [0, σj−1], the number of nonzero components of the optimal forgery and suppression strategies is i and n − j + 1, respectively. Further, the gradient of the privacy-forgery-suppression function at the origin is
Proof
The proof is presented in Appendix D.
Next, we shall derive an expression for the relative decrement of the privacy-risk function at ρ, σ ≃ 0. To this end, we define the forgery relative decrement factor
and the suppression relative decrement factor
By dint of Proposition 7, the first-order Taylor approximation of function (4) around ρ = σ = 0 yields
or more compactly, in terms of the decrement factors,
In words, the minimum and maximum ratios characterize the relative reduction in privacy risk. The following result, Proposition 8, establishes a bound on these relative decrement factors.
Proposition 8 (Relative Decrement Factors)
In the nontrivial case when q ≠ p, the relative decrement factors satisfy δρ > 1 and δσ > 0.
Proof
The proof is shown in Appendix D.
Conceptually, the bound on δρ tells us that the relative decrement in privacy risk is greater than the forgery rate introduced. This is under the assumption that q ≠ p and at low rates of forgery and suppression. The bound on δσ, however, is looser than the previous one and just ensures that an increase in the suppression rate always leads to a decrease in privacy risk, as one would expect.
4.5. Pure Strategies
In the previous subsections we investigated the forgery and the suppression of ratings as a mixed strategy that users may adopt to enhance their privacy. In this subsection we contemplate the case in which users may be reluctant to use these two mechanisms in conjunction; and as a consequence, they may opt for a pure strategy consisting in the application of either forgery or suppression. In this case, it would be useful to determine which is the most appropriate technique in terms of the privacy-utility trade-off posed. Our next result, Corollary 9, provides some insight on this, under the assumption that, from the user’s perspective, the impact on utility due to forgery is equivalent to that caused by the effect of suppression.
Before showing this result, observe from Theorem 3 that is the minimum forgery rate such that (ρ, 0) = 0. Analogously, is the minimum suppression rate satisfying (0, σ) = 0. In other words, ρn and σ1 are the critical rates of the pure forgery and suppression strategies, respectively. Further, note that σ1 < σ0 = 1, on account of the positivity assumption (5). However, ρn > 1 if, and only if, .
Corollary 9 (Pure Strategies)
Consider the nontrivial case when q ≠ p.
- (i)
The critical rates of the pure forgery and suppression strategies satisfy ρn < σ1 if, and only if,
- (ii)
The forgery and the suppression relative decrement factors satisfy δρ > δσ if, and only if,
Proof
Both statements are immediate from the definitions of ρn and σ1 on the one hand, and δρ and δσ on the other.
In conceptual terms, the condition ρn < σ1 means that the pure forgery strategy is the most appropriate mechanism in terms of causing the minimum distortion to attain the critical-privacy region. On the other hand, the condition δρ > δσ implies that, at low rates, the pure forgery strategy offers better privacy protection than the pure suppression strategy does. Therefore, the conclusion that follows from Corollary 9 is that, together with the quantity D(q || p), the arithmetic and geometric mean of the ratios and determine which strategy to choose. Since the choice of the pure strategy depends on each particular user and each particular application, obviously it is not possible to draw further general conclusions on which one is more convenient. Later on in Section 5, however, we shall investigate this issue in a real-world application and examine the percentage of users that would opt for either forgery or suppression as pure strategies.
Another interesting remark is the duality of these two ratios and . The former characterizes the minimum rate for the pure suppression strategy to reach the critical-privacy region and, at the same time, it establishes the privacy gain at low forgery rates. Conversely, the latter ratio defines the critical rate of the pure forgery strategy and determines the relative decrement in privacy risk at low suppression rates.
Lastly, we would like to establish a connection between our work and that of [27,29], where the pure forgery and suppression strategies are investigated. Denote by F the function derived in [27] modeling the trade-off between forgery rate and privacy risk, the latter being measured as the KL divergence between the user’s apparent profile and the population’s distribution. Define ρ′ as the ratio of forged ratings to total number of ratings. Accordingly, it can be shown that and that . On the other hand, denote by ℘S the function in [29] characterizing the trade-off between suppression rate and privacy gain. In this case, privacy is measured as the Shannon’s entropy of the user’s apparent profile. Under the assumption that the population’s profile is uniform, it can be proven that . In short, our formulation of the problem of optimal forgery and suppression of ratings encompasses, as particular cases, the cited works.
4.6. Numerical Example
This subsection presents a numerical example that illustrates the theoretical analysis conducted in the previous subsections. Later on in Section 5 we shall evaluate the effectiveness of our approach in a real scenario, namely in the movie recommendation system Movielens. In our numerical example we assume n = 3 categories of interests. Although the example shown here is synthetic, these three categories could very well represent interests across topics such as technology, sports and beauty. Accordingly, we suppose that the user’s rating distribution is
and the population’s,
Note that these distributions satisfy the positivity and labeling assumptions (5) and (6).
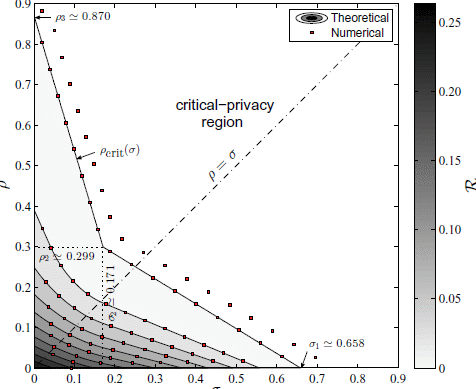
From Section 4.1, we easily obtain the forgery thresholds ρ1 = 0, ρ2 ≃ 0.299 and ρ3 ≃ 0.870 on the one hand, and on the other the suppression thresholds σ3 = 0, σ2 ≃ 0.171 and σ1 ≃ 0.658. The thresholds ρ3 and σ1 are the critical rates of the pure strategies. If we are to reach the critical-privacy region and do not have any preference for either forgery or suppression, the fact that ρ3 > σ1 leads us to opt for suppression as pure strategy. However, the geometric mean of and is approximately 0.799, which is lower than 2D(q || p) ≃ 1.20. On account of Corollary 9, this means that the pure forgery strategy contributes to a greater reduction in privacy risk at low rates than suppression does. In fact, the gradient of the privacy-forgery-suppression function at the origin is ∇(0, 0)T ≃ (−1.81,−0.639), by virtue of Proposition 7.
Figure 5 shows the contour lines of this function, computed analytically from Theorem 3 and numerically (c). The region plotted in gray shades corresponds to the noncritical-privacy region


Next, we examine the optimal apparent rating distribution for different values of ρ and σ. For this purpose, the user’s genuine distribution q, the population’s distribution p and the optimal apparent distribution t* are depicted in the probability simplices shown in Figure 6. In each simplex, we also represent the contour lines of the KL divergence D(· || p) between every distribution in the simplex and p. Further, we plot the set of feasible apparent user distributions, not necessarily optimal, for four different combinations of ρ and σ; in any of these cases, the set takes the form of a hexagon. Having said this, now we turn our attention to Figure 6a. In this case, the optimal forgery and suppression strategies have i = n−j+1 = 1 nonzero component, since ρ isin; [0, ρ2] and σ isin; [0, σ2]. This places the solution t* at one vertex of the hexagon. A remarkable fact is that, for these rates, the privacy risk is approximately halved. In the end, consistently with Proposition 8, the forgery and the suppression relative decrement factors are δρ ≃ 6.87 > 1 and δσ ≃ 2.42 > 0.
In the case shown in Figure 6b, r* still has i = 1nonzero components, while s* contains n−j+1 = 2 nonzero components. Geometrically, the optimal apparent distribution lies at one edge of the feasible region. This lowers privacy risk to a 19% of its initial value. The case in which (ρ, σ) = (ρcrit(σ), σ) is depicted in Figure 6c. Here, the number of nonzero components of r* and s* remains the same as in the previous case, but the privacy risk becomes zero. The last case, illustrated in Figure 6d, does not have any practical application, as (ρ, σ) = 0 for any (ρ, σ) isin; ∂ 
5. Experimental Evaluation
In this section we evaluate the extent to which the forgery and the suppression of ratings could enhance user privacy in a real-world recommendation system. The system chosen to conduct this evaluation is Movielens, a popular movie recommender developed by the GroupLens Research Lab [63] at the University of Minnesota. As many other recommenders, Movielens allows users to both rate and tag movies according to their preferences. These preferences are then exploited by the recommender to suggest movies that users have not watched yet.
5.1. Data Set
The data set that we used to assess our data-perturbative mechanism is the Movielens 10M data set [64], which contains 10,000,054 ratings and 95,580 tags. The ratings and tags included in this data set were assigned to 10,681 movies by 71,567 users. The data are organized in the form of quadruples (username, movie, rating, time), each one representing the action of a user rating a movie at a certain time. Usernames have been replaced with numbers in an attempt to anonymize the data set.
For our purposes of experimentation, we just needed the data fields username and movie, together with the categories each movie belongs to. Movielens contemplates n = 19 categories or movies genres, listed in alphabetical order as follows: action, adventure, animation, children’s, comedy, crime, documentary, drama, fantasy, film-noir, horror, IMAX, musical, mystery, romance, sci-fi, thriller, war and western. As we shall see later in Section 5.2, for each particular user, we shall have to rearrange those categories in such a way that the labeling assumption (6) is satisfied.
In our data set, all users rated, at least, 20 movies. This was the minimum number of ratings for the recommender to start working (d). After the elimination of those users who exclusively tagged movies, the total number of users reduced to 69,878. We found that only 4,099 of those users satisfied the positivity assumption (5). Although we commented in Section 4 that our analysis is also valid for nonstrictly positive distributions, our experimental analysis was conducted with profiles which do satisfy the aforementioned assumption, in particular with those 4,099 users. We decided to use strictly positive profiles as a procedure for eliminating outliers, since, in practice, for an appropriately representative choice of topic categories and a large volume of data, nearly all users should have a minimal interest in all those categories.
Considering that this small group of users represents just the 5.8% of the total number of users, we can assume that the application of our technique will have a negligible effect on the population’s profile p, as supposed in Section 3.4.
5.2. Results
In this subsection we examine how the forgery and the suppression of ratings may help users of Movielens to enhance their privacy. With this aim, first, we analyze the effect of the perturbation of ratings on the privacy protection of two particular users from our data set. Secondly, we consider the entire set of 4,099 users and assess the relative reduction in privacy risk when these users apply the same forgery and suppression rates. Lastly, we investigate the forgery and the suppression strategies separately, and draw some conclusions about these two pure strategies.
To conduct our first experiments, we choose two users with rather different profiles, in particular those identified by the numbers 3301 and 26589 in [64]. For the sake of brevity, we shall denote these users by v1 and v2, respectively. Before perturbing the movie rating history of these two users, it is necessary that the components of their actual profiles and the population’s distribution be rearranged to satisfy the labeling assumption (6). Table 1 shows how movie categories have been sorted, and then indexed from 1 to n, to fulfill the assumption above.
Figure 7a depicts the actual profile of v1 as well as the population’s distribution, the latter being computed by averaging across the 69,878 users. From this figure we note that the interests of this user far exceeds the population’s in categories such as musical, romance, IMAX, drama and documentary. More precisely, such ratios yield
In this figure, we also observe that the user’s interest and the population’s in the category 17 are nearly zero, namely q17 ≃ 0.0005 and p17 ≃ 0.0003. On the other hand, Figure 7a indicates that v1 shows little interest, compared to the population’s preferences, in categories such as animation, action, film-noir or children’s, to name just a few. Specifically, the first five smallest ratios yield
Figure 7b and 7c show the optimal forgery and suppression strategies that this particular user should apply, in the case when σ = 0.150 and ρcrit(σ) ≃ 0.180. The solutions plotted in these figures are consistent with our two previous observations—the optimal forgery strategy recommends that the user submit false ratings to movies falling into the categories where the ratio is low; and the optimal suppression strategy suggests that the user refrain from rating movies belonging to categories where the ratio is high. Just as an example, the fact that means that the user at hand should eliminate one in five ratings to movies classified as IMAX.
Figure 8a represents the population’s item distribution and the genuine profile of the second user, υ2. As this figure illustrates, the interests of this user differ significantly from those of υ1. The categories where υ2 shows too much interest (compared to the population’s profile) are action, animation, fantasy, adventure and IMAX, categories where the ratios are rather low for υ1. More specifically, the ratios for this second user are
Another important difference between these users is that the quotient for υ1 is greater than that for υ2. Since , the latter user will need therefore a higher pure forgery rate than that required by the former user to achieve the critical-privacy region. At the same time, we observe from Figure 8a that the first five smallest ratios of user υ2 yield
These indexes correspond, more precisely, to the categories musical, western, film-noir, horror and drama. Because , we also note from Equation (31) that the pure suppression rate needed to achieve the critical-privacy region will be lower than that required by υ1. Figure 8b and 8c show the optimal strategies to be adopted by υ2 in order for their apparent profile to become the population’s distribution. This is in the special case when this user accepts eliminating and forging σ = 20% and ρcrit(σ) ≃ 10.5% of their ratings, respectively.
Figure 9 represents the optimal trade-off surfaces among privacy, forgery rate and suppression rate for our two concrete users. In this figure we plot the contour levels of the two functions (ρ, σ), which we computed theoretically. As for user υ1, the initial privacy risk is (0, 0) ≃ 0.101 and the arithmetic mean between the ratios and yields approximately 1.37. Since the mean is higher than 1, Corollary 9 tells us that this user should opt for suppression as pure strategy, in lieu of forgery. This is under the assumption that they wish to achieve the minimum privacy risk and do not have any preference for any of the pure strategies. Nevertheless, the fact that δρ ≃ 12.6 > δσ ≃ 10.9 leads us to choose forgery as pure strategy for ρ, σ ≃ 0. When both strategies are combined, note that a forgery and suppression rate of just 0.1% leads to a relative reduction in privacy risk of 2.35%, on account of the first-order Taylor approximation derived in Section 4.4.
The differences observed in Figures 7a and 8a between υ1 and υ2 are also evidenced in Figure 9a and 9b. The initial privacy risk for υ2 is (0, 0) ≃ 0.079 and the arithmetic mean between the minimum and maximum ratios is approximately 0.887. This latter result implies that this user should choose forgery instead of suppression as pure strategy. This is an effect that we anticipated previously and that can also be seen immediately from Figure 9b, on account of the fact that ρn ≃0.516 < σ1 ≃ 0.742. Another interesting observation is that δρ≃25.8 > δσ ≃ 6.62, which means that, for low perturbation rates, forgery provides almost 4 times more reduction in privacy risk than suppression does. In light of this, we may conclude that, for this particular user, the pure forgery strategy is more convenient than suppression, not only at low rates but also when they want to attain the critical-privacy region.
In Figure 9a we have also plotted 4 points, which correspond to the following pairs of values (ρ, σ): (0.03, 0.04), (0.06, 0.08), (0.11, 0.12) and (0.18, 0.15). For each of these pairs, we have represented in Figure 10 the quotient corresponding to the user υ1. The aim is to show how the optimal apparent profile becomes proportional to the population’s distribution, as this user approaches the critical-privacy region. Figure 10a considers the first pair of values. Here, ρ and σ fall into the intervals [ρ6, ρ7] and [σ18, σ17], respectively. Consistently with Proposition 5, we check that and that .
In Figure 10b we double the rates of forgery and suppression. On the one hand, this leads to . On the other, the fact that σ ∈ [σ15, σ14] implies that . It is also interesting to note that, for these relatively small values of ρ and σ, the final privacy risk is 26% of the initial value D(q || p).
As ρ and σ increase, so does the function φ. The contrary happens with the function χ, which decreases with both rates. In Figure 10c, for example, the proportionality relationship between t* and p holds for all except 4 categories. The last pair (ρ, σ) ≃ (0.18, 0.15) lies at the boundary of

Having examined the case of two specific users, in our next series of experiments we evaluate the privacy-protection level that all users can achieve if they are disposed to forge and eliminate a fraction of their ratings. For simplicity, we suppose that the 4099 users apply a common forgery rate and a common suppression rate. Figure 11 depicts the contours of the 10th, 50th and 90th percentile surfaces of relative reduction in privacy risk, for different values of ρ and σ. Two conclusions can be drawn from this figure.
First, for relatively small values of ρ and σ (lower than 15%), a vast majority of users lowered privacy risk significantly. In quantitative terms, we observe in Figure 11a that, for ρ = σ = 0.05, the 90% of users adhered to our technique obtained a reduction in privacy risk greater than 52.4%. For those same rates of forgery and suppression, the 50th and 90th percentiles are 73.9% and 94.8%. For higher rates, e.g., ρ = σ = 0.13, Figure 11b shows that half of users experienced a reduction in privacy risk equal to 100%.
Secondly, the three percentile surfaces exhibit a certain symmetry with respect to the line ρ = σ. If this symmetry were exact, the exchange of the rates of forgery and suppression would not have any impact on the resulting privacy-protection achieved. However, this is not the case. For example, Figure 11a shows a lower reduction in privacy risk for ρ < σ, particularly accentuated when σ ≃ 0. The reason for this may be found in the fact that, for most users, ρn is greater than σ1. We shall elaborate more on this later on when we consider forgery and suppression as pure strategies.
Next, we analyze the privacy protection provided by our technique for ρ, σ ≃ 0. In the theoretical analysis conducted in Section 4.4 we derived an expression for the relative reduction in privacy risk at low rates. Particularly, said expression was in terms of two factors, namely δρ and δσ. In Figure 12 we show the probability distribution of these factors. Consistently with Proposition 8, the minimum values of these factors are δρ ≃ 3.12 > 1 and δσ ≃ 2.30 > 0. The maximum values attained by these forgery and the suppression factors are approximately 324.98 and 266.13. On the other hand, in favour of suppression is the fact that the percentage of users with δρ ≥ 30 is lower than those users with δσ ≥ 30. More precisely, these percentages yield 26.8% and 33.1%, respectively. In the end, an eye-opening finding is that δρ > δσ in 43.45% of users, which suggests introducing a suppression rate higher than that of forgery, at least at low rates.
After analyzing the forgery and the suppression of ratings as a mixed strategy, our last experimental results contemplate the application of forgery and suppression as pure strategies. In Figure 13 we illustrate the probability distribution of the critical rates ρn and σ1. The critical forgery rate ranges approximately from 0.171 to 54.18, and its average is 3.45. The critical suppression rate, on the other hand, goes from 0.153 to 0.963, and its average is 0.632. These figures indicate that, on average, a user will have either to refrain from rating an item six out of ten times, or submit nearly 3.45 false ratings per each original rating. This is, of course, when the user wishes to reach the critical-privacy region. Bearing these figures in mind, it is not surprising then that 95.3% of the users in our data set would opt for suppression as pure strategy, as it comes at the cost of a lower impact on utility.
6. Conclusions
In the literature of recommendation systems there exists a variety of approaches aimed at protecting user privacy. Among these approaches, the forgery and the suppression of ratings emerge as a technique that may hinder attackers in their efforts to accurately profile users on the basis of the items they rate. Our technique does not require that users trust neither the recommender nor the network operator, it is simple in terms of infrastructure requirements, and it can be used in combination with other approaches providing soft privacy. However, as any data-perturbative approach, our privacy-enhancing technology comes at the expense of a loss in data utility, in particular a degradation of the quality of the recommender’s predictions. Put another way, it poses a trade-off between privacy and utility.
The objective of this paper is to investigate mathematically said trade-off. For this purpose, first we propose a quantitative measure of both privacy and utility. We quantify privacy risk as the KL divergence between the user’s rating distribution and the population’s, and measure utility as the fraction of ratings the user is willing to forge and suppress. With these two quantities, we formulate a multiobjective optimization problem characterizing the trade-off between privacy risk on the one hand, and on the other forgery rate and suppression rate.
Our theoretical analysis provides a closed-form solution to this problem and characterizes the optimal trade-off surface between privacy and utility. The solution is confined to the closure of the noncritical-privacy region. The interior of the critical-privacy region is of no interest as the privacy risk attains its minimum value at the boundary of

Our theoretical study also examines how these optimal strategies perturb user profiles. It is interesting to observe that the optimal apparent profile becomes proportional to the population’s distribution in those categories with the lowest and highest ratios . Our analysis also includes the characterization of at low rates of forgery and suppression. More accurately, we provide a first-order Taylor approximation of the privacy-utility trade-off function, from which we conclude that the ratios and determine, together with the quantity D(q || p), the privacy risk at low rates. An eye-opening fact is that the relative decrement in privacy risk is greater than the forgery rate introduced.
Further, we consider the special case when forgery and suppression are not used in combination. Under this consideration, we investigate which one is the most appropriate technique, first, in terms of causing the minimum distortion to reach the critical-privacy region, and secondly, in terms of offering better privacy protection at low rates. Our findings show that the arithmetic and geometric mean of the maximum and minimum ratios play a fundamental role in deciding the best technique to use.
Afterwards, our formulation and theoretical analysis are illustrated with a numerical example.
In the end, the last section is devoted to the experimental evaluation of our data-perturbative mechanism in a real-world recommendation system. In particular, we examine how the application of the forgery and the suppression of ratings may preserve user privacy in Movielens. Among other results, we find that a large majority of users significantly reduce privacy risk for forgery and suppression rates of just 13%. Moreover, we observe that the mixed strategy may provide stronger privacy protection for the same total rate than the pure strategies. In our data set, the probability distributions of the relative decrement factors indicate that, at low rates, forgery provides a higher reduction in privacy risk than suppression does. By contrast, we notice that the suppression relative decrement factor is greater than that of forgery in 56.55% of users. Lastly, we consider the case when users must opt for either forgery or suppression; and find that the latter is the best strategy to use in 95.3% of users who wish to vanish privacy risk while causing the minimum distortion.
Acknowledgments
This work was partly supported by the Spanish Government through projects Consolider Ingenio 2010 CSD2007-00004 “ARES”, TEC2010-20572-C02-02 “Consequence” and by the Government of Catalonia under grant 2009 SGR 1362.
Appendix
A. Closed-Form Solution
In this appendix, we provide the proofs of the theoretical results included in Section 4.1, namely, Lemma 1, Proposition 2 and Theorem 3.
Proof of Lemma 1
The proof of statement (i) consists of two steps. In the first step, we show that the optimization problem stated in the lemma is convex; then we apply Karush-Kuhn-Tucker (KKT) conditions to said problem, and finally reformulate these conditions into a reduced number of equations. The bulk of this proof comes later, in the second step, where we proceed to solve the system of equations for the two cases considered in the lemma, ψ < ω and ψ = ω. Lastly, statements (ii) and (iii) follow from (i).
To see that the problem is convex, simply observe that the objective function is convex on account of H(fk) ≽ 0, and that the inequality and equality constraint functions are affine. Since the objective and constraint functions are also differentiable and Slater’s constraint qualification holds, KKT conditions are necessary and sufficient conditions for optimality [62]. Systematic application of these optimality conditions leads to the Lagrangian cost,
and finally to the conditions
Because , it follows from the dual optimality conditions that κk+xk−yk > 0, which implies, by complementary slackness, that νk = 0. Subsequently, we may rewrite the dual optimality conditions as λk = hk(xk, yk) – ψ and μk = ω – hk(xk, yk). By eliminating the slack variables λk, μk, we obtain the simplified conditions hk(xk, yk) ≥ ψ and hk(xk, yk) ≤ ω. Lastly, we substitute the above expressions of λk and μk into the complementary slackness conditions, so that we can formulate the dual optimality and complementary slackness conditions equivalently as
In the following, we shall proceed to solve these equations which, together with the primal and dual feasibility conditions, are necessary and sufficient conditions for optimality. To this end, first note that, if ψ > ω, then there exists no (xk, yk) that satisfies Equations (35) and (36) at the same time, and consequently, as stated in part (i) of the lemma, there is no solution. Concordantly, next we shall study the case when ψ < ω; afterwards we shall tackle the other case when ψ = ω.
Before plunging into the analysis of the former case, recall that the function hk is strictly increasing in xk and strictly decreasing in yk. Having said this, observe that, under the assumption ψ < ω, the variables xk and yk cannot be positive simultaneously by virtue of Equations (37) and (38). Bearing this in mind, consider these three possibilities for each k: hk(0, 0) < ψ, ψ ≤ hk(0, 0) ≤ ω and ω < hk(0, 0).
When hk(0, 0) < ψ, the only conclusion consistent with (35) and with the fact that hk is strictly increasing in xk is that xk > 0. Since xk must be positive, the complementary slackness condition (37) implies that hk(xk, yk) = ψ and, because of (38), that yk = 0. As a result, xk must satisfy hk(xk, 0) = ψ, or equivalently, . Next, we show that the solution (xk, 0) is unique. For this purpose, suppose that yk > 0 and, in consequence, that xk = 0. It follows from (38), however, that hk(0, yk) = ω, which contradicts the fact that hk is a strictly decreasing function of yk. In the end, we verify that xk = yk = 0 does not satisfy (35) and thus prove that is the unique minimizer of the objective function when hk(0, 0) < ψ.
Now consider the case when ψ ≤ hk(0, 0) ≤ ω. First, suppose that xk > 0, and therefore that yk = 0. By complementary slackness, it follows that hk(xk, 0) = ψ, which is not consistent with the fact that hk is strictly increasing in xk. Consequently, xk cannot be positive. Secondly, assume that xk is zero and yk positive. Under this assumption, Equation (38) implies that hk(0, yk) = ω, a contradiction since hk is a strictly decreasing function of yk. Accordingly, yk cannot be positive either. Finally, check that xk = yk = 0 satisfies the optimality conditions and hence it is the unique solution.
The last possibility corresponds to the case when ω < hk (0, 0). Note that, in this case, the only conclusion consistent with (36) and with the fact that hk is strictly decreasing in yk is that yk > 0. Thus, because of (38), yk must satisfy hk(0, yk) = ω. Recalling from the lemma that hk(xk, yk) = hk(xk − yk, 0), we may express the condition hk(0, yk) = ω equivalently as . Lastly, we check that this solution is unique in the case under study. To this end, note that a solution such that xk > 0 and yk = 0 contradicts the fact that hk is strictly increasing in xk. As a result, xk cannot be positive. Finally, we confirm that Equation (36) does not hold for xk = yk = 0 and therefore prove that is the unique solution when ω < hk(0, 0).
In summary, if hk(0, 0) < ψ, or equivalently, ; otherwise xk = 0. Further, if hk(0, 0) > ω, or equivalently, ; otherwise yk = 0. Accordingly, we may write the solution compactly as
where ψ, ω must satisfy the primal equality constraints ∑k xk = η and ∑k yk = θ.
Having examined the case when ψ < ω, next we proceed to solve the optimality conditions at hand for ψ = ω. Observe that, in this new case, Equations (35) and (36) transform into the equation
Moreover, note that any pair (xk, yk) satisfying (40) also meets the complementary slackness conditions (37) and (38). However, notice that this does not mean that all those pairs are optimal. To elaborate on this point, consider the following three possibilities for each k: hk(0, 0) < ψ, hk(0, 0) = ψ and ψ < hk(0, 0).
In the case when hk(0, 0) < ψ, the only condition consistent with (40) and with the fact that hk is strictly increasing in xk is that xk > 0. From the lemma, it is immediate that , which implies that xk must also be greater than yk. Hence, the set of solutions is
where every pair in this set must also fulfill the primal equality conditions. Let satisfy , or equivalently, . Then, because for any α ≥ 0, this set may be recast equivalently as
For the two remaining cases, i.e., hk(0, 0) = ψ and ψ < hk(0, 0), the set of solutions is obtained in a completely analogous way as above. In the former case, the pairs (xk, yk) must satisfy xk = yk, and the set of solutions may be expressed as
In the latter case, it follows that yk > xk and, consequently, that the set of solutions is
where must satisfy .
To sum up, the case ψ = ω leads to the following solutions: if hk(0, 0) < ψ, or equivalently, ; otherwise xk = αk. In addition, if hk(0, 0) > ω, or equivalently, ; otherwise yk = αk. Accordingly, the solutions (xk, yk) yield
for some ψ, ω and nonnegative sequence α1, . . . , αn such that ∑k xk = η and ∑k yk = θ. Note that, although ψ = ω, we intentionally write ω in the second term instead of ψ to highlight that the solutions for ψ < ω and for ψ = ω just differ in the term αk, as we claimed in part (i) of the lemma.
To complete the proof of statement (i), it suffices to show that the number of solutions is infinite when ψ = ω. To this end, simply observe that there exists an infinite number of sequences α1, . . . , αn such that
and
which results in an infinite number of solutions of the form given in Equation (45).
Now we proceed to prove (ii), which is an immediate consequence of (i). For this purpose, observe that if ψ ≤ hi+1(0, 0) ≤ · · · ≤ hn(0, 0) holds for some i = 0, . . . , n − 1, then , and accordingly xi+1 = · · · = xn = 0. Similarly, if h1(0, 0) ≤ · · · ≤ hj−1(0, 0) ≤ ω is satisfied for some j = 2, . . . , n + 1, then , and thus y1 = · · · = yj−1 = 0.
Note that the particular case when the index i ranges from 1 to j −1 and the index j goes from 2 to n is the case described in (ii) (a), which corresponds to η, θ > 0. Further, observe that the case assumed in (ii) (b), i.e., when j = n + 1, implies that θ = 0. Here, the index i starts at 1, therefore excluding η = 0, and ends at n, including the possibility that xi > 0 for all i. In part (ii) (c), we consider i = 0, which is equivalent to the condition η = 0. In this case, the index j starts at 1, permitting yj > 0 for all j, and ends at n, avoiding θ = 0. Finally, the case described in (ii) (d), namely when j = n + 1 and i = 0, is precisely the trivial case x = y = 0.
In order to verify statement (iii), we proceed analogously by noting that if ψ = hi+1(0, 0) = · · · = hj−1(0, 0) holds for some i = 1, . . . , j − 2 and some j = 3, . . . , n, then , and consequently xk = yk = αk for k = i + 1, . . . , j − 1.
Proof of Proposition 2
The first statement can be shown from the definition of the forgery thresholds by routine algebraic manipulation and under the labeling assumption (6). To this end, it is helpful to note that
The second statement can be shown analogously, observing that
For the last statement, use the definitions of the forgery and the suppression thresholds to note that the condition ρj(σ) ≥ ρj−1 is equivalent to σ ≤ σj−1.
Proof of Theorem 3
The proof is structured as follows. We begin by showing that the optimization problem (4) may be construed as a particular case of that stated in Lemma 1. Accordingly, we apply this lemma, namely the cases (ii) and (iii), to obtain the optimal forgery and suppression strategies. The application of the former case allows us to derive the solution for (ρ, σ) ∈


Use the definition of KL divergence to write the objective function of the optimization problem as , with . Observe that the functions are twice differentiable on {(rk, sk) : qk + rk − sk > 0}. Denote by hk the derivative of fk with respect to rk,
Then, note that the functions fk and hk satisfy the assumptions of Lemma 1, and that the inequality and equality constraints of function (4) coincide with those in the lemma. This exposes the structure of the optimization problem as a special case of the resource allocation lemma.
Before proceeding any further, notice from Equation (50) that hk(rk, 0) is a strictly increasing function of rk and hence invertible. Note also that, according to the lemma, the solutions are completely determined by the inverse of this function, which is denoted by and yields
Finally, observe that the assumption h1(0, 0) ≤ · · · ≤ hn(0, 0) in the lemma is equivalent to the labeling assumption (6), as hk(0, 0) is a strictly increasing function of .
Next we apply Lemma 1 (ii), where it is assumed the condition ψ < ω. We start with case (ii) (a). On account of part (i) of the lemma, the optimal forgery strategy must satisfy
or equivalently,
Analogously for the suppression strategy,
and therefore
Then it suffices to substitute the expressions of ψ and ω into the function , to obtain the nonzero optimal solutions claimed in assertion (ii) of the theorem.
Now we proceed to confirm the interval of values of ρ and σ where these solutions are defined. In the case under study, ψ and ω satisfy hi(0, 0) < ψ ≤ hi+1(0, 0) for some i = 1, . . . , j − 1 and hj−1(0, 0) ≤ ω < hj (0, 0) for some j = 2, . . . , n. We split the discussion into two cases, namely i < j − 1 and i = j − 1.
Assume the former case. Observe that the condition hi(0, 0) < ψ is equivalent to
and finally, after routine algebraic manipulation, to
Similarly, the upper-bound condition ψ ≤ hi+1(0, 0) leads to
Hence, the intervals resulting from imposing hi(0, 0) < ψ ≤ hi+1(0, 0) are of the form (ρi, ρi+1]. The monotonicity of the thresholds ρi, demonstrated in Proposition 2, guarantees that these intervals are contiguous and nonoverlapping. In an analogous manner, it can be shown that the condition hj−1(0, 0) ≤ ω < hj (0, 0) leads to intervals of the form (σj, σj−1], also contiguous and nonoverlapping by virtue of Proposition 2.
Now assume the latter case, where hi(0, 0) < ψ < ω < hj(0, 0) with i = j − 1. On the one hand, the assumption hj−1(0, 0) < ψ is, as shown above, equivalent to the condition ρ > ρj−1. On the other hand, straightforward manipulation allows us to write the inequality ψ < ω as
Combining these two bounds on ψ, we obtain the interval (ρj−1, ρcrit(σ)). With this last interval, we complete the range of validity of the solution for the case (ii) (a) in the lemma. Ultimately, it is easy to verify that, in those intervals of ρ and σ, the optimal apparent profile does not coincide with the population’s profile p. In consequence, D(t _ p) > 0.
Next, we turn to case (ii) (b) of the lemma. Here, the assumption hn(0, 0) ≤ ω leads to σ = 0, or equivalently, to the solution s = 0. Note that, precisely, this is the solution given in the theorem for σ = σj with j = n. On the other hand, the application of the condition
results in the same optimal forgery strategy obtained in case (ii) (a). Proceeding analogously as in this case, from the assumptions on ψ we derive the intervals of values of ρ where the solution is defined: (ρi, ρi+1] for i = 1, . . . , n − 1 and (ρi, ρi+1) for i = n. Given these intervals, it is then straightforward to check that R(ρ, 0) = 0 if, and only if, ρ ≥ ρn. This provides us with the pairs (ρ, 0) that belong to cl

In case (ii) (c), the condition ψ ≤ h1(0, 0) means that ρ = 0, or equivalently, r = 0. Observe that this is the solution stated in the theorem for ρ = ρi with i = 1. Then again, the condition
leads to the same optimal suppression strategy found in case (ii) (a). From the assumptions in the lemma on ω, we obtain the intervals (σj, σj−1] for j = 2, . . . , n and (σj, σj−1) for j = 1. Then, we verify that R(0, σ) = 0 if, and only if, σ ≥ σ1, from which it follows the pairs (0, σ) that belong to cl

Finally, the case (ii) (d) in the lemma, in which hn(0, 0) ≤ ω and ψ ≤ h1(0, 0), corresponds to the trivial case σ = σj for j = n and ρ = ρi for i = 1, that is, the solution r = s = 0.
After having applied Lemma 1 (ii) to function (4), now we proceed with case (iii) (a). In applying it, we shall show that the solution claimed in the theorem is also valid for the extreme values of the intervals in case (ii) (a), specifically the set
Assume the case (iii) (a) in which hi(0, 0) < ψ = ω < hj (0, 0) for some j = 2, . . . , n and i = j − 1. Under this assumption, the equality constraint in the lemma is equivalent, after simple algebraic manipulation, to
where we define . Similarly, the equality constraint becomes
But ψ = ω, therefore
or equivalently,
In short, the assumption ψ = ω imposes the condition (ρ, σ) ≽ (ρcrit(σ), σ) for some nonnegative sequence α1, . . . , αn satisfying the above equality. Next we examine, for a given σ, these two possibilities, ρ = ρcrit(σ) and ρ > ρcrit(σ).
Consider the former possibility and observe that ρ = ρcrit(σ) if, and only if, αk = 0 for k = 1, . . . , n. According to the lemma, the nonzero optimal solutions yield
for k = 1, . . . , j − 1, and
for k = j, . . . , n, that is, the solutions obtained after applying case (ii) (a), but evaluated at ρ = ρcrit(σ). From these expression for r and s, it is immediate to verify then that t = p and thus R(ρ, σ) = 0.
Now we assume the latter possibility, i.e., (ρ, σ) ≻ (ρcrit(σ), σ), to show that the privacy-risk function also vanishes for these values of ρ and σ. On account of part (iii) (a) of the lemma and (61), we derive the optimal forgery and suppression strategies
and sk = αk for k = 1, . . . , j − 1, and
and rk = αk for k = j, . . . , n. Then, we substitute r and s back into the apparent profile t and check that D(t _ p) = 0. In doing so, we determine the pairs (ρ, σ) ≻ 0 that belong to cl

To conclude the proof, it remains only to write the privacy-risk function in terms of the optimal apparent distribution. With this aim, we split the summation into three parts. The first part, corresponding to is
where we leverage on the fact that does not depend on k. The second part of the sum, corresponding to yields
The last part, corresponding to , is
where we also note that does not depend on k either. Now, it is straightforward to identify the terms of R(ρ, σ) as the KL divergence between the distributions
and
precisely the distributions stated in the theorem.
B. Orthogonality, Continuity and Proportionality
This appendix provides the proof of the results shown in Section 4.2, in particular, Corollary 4 and Proposition 5.
Proof of Corollary 4
The proof of (i) is trivial from Theorem 3. To prove statement (ii) we also resort to this theorem. According to it, each component may be regarded as a piecewise function of ρ defined on the contiguous, nonoverlapping intervals [ρi, ρi+1] for i = 1 and (ρi, ρi+1] for i = 2, . . . , j−1. A direct verification shows that, for any k = j, . . . , n, the component is identically zero on the whole interval [ρ1, ρj ] and hence continuous. For any k = 1, . . . , j − 1, we immediately check the continuity of on the interior of each of the intervals parameterized by i. Now we examine the endpoints of such intervals. The continuity at the extreme points ρ1 and ρj is verified straightforwardly as the intervals are closed at these points. Then, we check that the limit at the remaining endpoints ρi exists, since
for i = 2, . . . , j − 1. Because each limit coincides with the corresponding value , we prove the continuity of the components r1, . . . , rj−1. The proof of the continuity of the components of s* is analogous to that of r*.
Proof of Proposition 5
The continuity of the components of t* on cl

Next, we proceed to demonstrate the strict monotonicity of φ. A simple calculation shows that
To prove that , it is sufficient to verify that .Q̄j > σj−1, or equivalently, that . Then, by the positivity assumption (5), we immediately see that this latter inequality holds for any j = 2, . . . , n. The strict monotonicity of φ in σ also follows from assumption (5).
To complete (ii), we write the condition φ(ρ, σ) ≤ 1 as
A routine computation shows that the equality holds for ρj(σ) and any σ ∈ [σj, σj−1] with j = 2, . . . , n. Therefore, for any fixed σ, the inequality holds strictly for any other ρ. The converse, that is, φ(ρ, σ) = 1 implies (ρ, σ) = (ρj(σ), σ), is immediate from the strict monotonicity of φ. The proof of statement (iii) proceeds along the same lines of that of (ii) and is omitted.
C. Critical-Privacy Region
Next, we provide the proof of Proposition 6, included in Section 4.3.
Proof of Proposition 6
From Theorem 3, it is routine to check the continuity of ρj on [σn, σ1]. To show its convexity, we conveniently write this function as ρj(σ) = mj σ + bj , where and . Next, we prove that the slopes satisfy mj < mj−1 for all j = 3, . . . , n. We proceed by contradiction, assuming that mj ≥ mj−1. Note that this inequality is equivalent to Pj−1 . P̄j−1 ≤ P̄j – . P̄j . P̄j−1 and, after algebraic simplification, to pj−1 ≤ 0. This contradicts the positivity assumption (5), which, in turn, implies that mj < 0 for all j = 2, . . . , n. Therefore, since ρj is a piecewise linear function defined by the strictly increasing sequence of negative slopes {mn, . . . , m2}, we can conclude that ρj is convex. This proves statement (i). The second statement follows from the first one. As ρj is convex, so is its epigraph, i.e., the critical-privacy region.
D. Case of Low Forgery and Suppression
Finally, this appendix provides the proofs of the theoretical results shown Section 4.4, namely, Propositions 7 and 8.
Proof of Proposition 7
The existence of the indexes i and j is guaranteed by the assumption that q _= p. The number of nonzero components of r* and s* is trivial from Theorem 3. In view of this theorem, for any ρ ∈ [0, ρi+1] and σ ∈ [0, σj−1], we have
The continuity of the components of r* and s* proven in Corollary 4 (ii) ensures the continuity of the privacy-forgery-suppression function on

On account of Proposition 2, the conditions ρ1 = · · · = ρi and σj = · · · = σn imply
and
Therefore,
The derivative of R with respect to ρ at ρ = σ = 0 follows analogously.
Proof of Proposition 8
Observe that the statement δρ > 1 is equivalent to the condition q1 < p1. We prove this by contradiction. Suppose that q1 > p1. By the labeling assumption (6), it follows that qk > pk for all k, what leads to the contradiction that 1 = ∑qk > ∑pk = 1. Now assume that q1 = p1. Since q _= p, there must exist an index i such that
But this implies that
a contradiction. This proves the first part of the proposition.
For the second part, note that the statement δσ > 0 is equivalent to
and, after algebraic manipulation, to
The positivity and labeling assumptions (5) and (6) ensure that all terms in the sum are nonpositive. However, the additional assumption q _= p implies that , which in turn implies that the first term is negative and so is, consequently, the entire summation.
Conflicts of Interest
The authors declare no conflicts of interest.
- *Some parts of this paper (a reduced version of Sections 1 and 2) were presented at the International Workshop on Data Privacy Management, Leuven, Belgium, September 2011 [1]. The formulation of the trade-off between privacy and utility (Section 3), the current theoretical analysis (Section 4), the experimental work (Section 5), the conclusions (Section 6) and the proofs given in the Appendices are all new work.
- (a)A recent survey [50] reports that 69% of the respondents just trust themselves when it comes to protecting their own personal information online.
- (b)The description of an architecture implementing this data-perturbative approach may be found in [1].
- (c)The numerical method chosen is the interior-point algorithm [62] implemented by the Matlab R2012b function fmincon.
- (d)Nowadays, the algorithm implemented by Movielens requires only 15 ratings to start generating predictions.
- Author ContributionsAll authors made substantial contributions to conception and design. J. P.-A. conducted the theoretical and experimental analysis, and wrote the manuscript. D. R.-M. contributed to the formulation of the problem and, together with J. F., directed and made critical revision of the manuscript for important intellectual content at all stages of preparation. All authors gave final approval of the version to be submitted and any revised version.
References
- Parra-Arnau, J.; Rebollo-Monedero, D.; Forné, J. A privacy-protecting architecture for collaborative filtering via forgery and suppression of ratings. Proceedings of the International Workshop Data Private Management (DPM), Leuven, Belgium, 15–16 September 2011; 7122, pp. 42–57.
- Hanani, U.; Shapira, B.; Shoval, P. Information filtering: Overview of issues, research and systems. User Model. User-Adap. Interact 2001, 11, 203–259. [Google Scholar]
- Oard, D.; Kim, J. Implicit Feedback for Recommender Systems. Proceedings AAAI Workshop Recommender System, Madison, WI, USA, 27 July 1998; pp. 81–83.
- Adomavicius, G.; Tuzhilin, A. Toward the next generation of recommender systems: A survey of the state-of-the-art and possible extensions. IEEE Trans. Knowl. Data Eng 2005, 17, 734–749. [Google Scholar]
- Su, X.; Khoshgoftaar, T.M. A survey of collaborative filtering techniques. Adv. Artif. Intell 2009, 2009. Article No. 4. [Google Scholar]
- Cranor, L.F. ‘I Didn’t Buy it for Myself’: Privacy and Ecommerce Personalization. Proceedings of the Workshop Private Electronic Society, Washington, DC, USA, 30 October 2003; pp. 111–117.
- Narayanan, A.; Shmatikov, V. Robust De-anonymization of Large Sparse Datasets. Proceedings IEEE Symposium Security Privacy (SP), Washington, DC, USA, 16 February 2008; pp. 111–125.
- Netflix prize, Available online: http://en.wikipedia.org/wiki/NetflixPrize accessed on 9 January 2014.
- Zaslow, J. If TiVo thinks you are gay, here’s how to set it straight. Available online: http://online.wsj.com/news/articles/SB1038261936872356908 accessed on 10 January, 2014.
- Bilton, N.; Stelter, B. Sony says Playstation hacker got personal data. Available online: http://www.nytimes.com/2011/04/27/technology/27playstation.html accessed on 18 February 2014.
- Ovide, S. Evernote discloses security breach. Available online: http://online.wsj.com/article/SB10001424127887323478304578336373531236296.html accessed on 2 March 2013.
- AOL search data scandal, Available online: http://en.wikipedia.org/wiki/AOLsearchdatascandal accessed on 12 February 2014.
- Last.fm privacy policy, Available online: http://www.lastfm.es/legal/privacy accessed on 12 February 2014.
- Helft, M. U.S. judge orders youtube to hand over video logs. Available online: http://www.nytimes.com/2008/07/03/technology/03iht-04youtube.14219540.html?r=0 accessed on 10 February 2014.
- Fox, S. Trust and Privacy Online: Why Americans Want to Rewrite the Rules; Pew Charitable Trusts: Philadelphia, PA, USA, 2000. [Google Scholar]
- Hoffman, D.L.; Novak, T.P.; Peralta, M. Building consumer trust online. Commun. ACM 1999, 42, 80–85. [Google Scholar]
- Parra-Arnau, J.; Rebollo-Monedero, D.; Forné, J. Measuring the privacy of user profiles in personalized information systems. Future Gen. Comput. Syst 2014, 33, 53–63. [Google Scholar]
- Rebollo-Monedero, D.; Parra-Arnau, J.; Forné, J. An information-theoretic privacy criterion for query forgery in information retrieval. Proceedings of the International Conference Security Technology (SecTech), Jeju Island, Korea, 8–10 December 2011; 259, pp. 146–154.
- Polat, H.; Du, W. Privacy-preserving collaborative filtering using randomized perturbation techniques. Proceedings of the SIAM International Conference Data Mining (SDM), San Francisco, CA, USA, 1–3 May 2003.
- Kargupta, H.; Datta, S.; Wang, Q.; Sivakumar, K. On the privacy preserving properties of random data perturbation techniques. Proceedings of the IEEE International Conference Data Mining (ICDM), Washington, DC, USA, 19–22 November 2003; pp. 99–106.
- Huang, Z.; Du, W.; Chen, B. Deriving private information from randomized data. Proceedings of the ACM SIGMOD International Conference Management Data, Baltimore, MD, USA, 14–16 June 2005; pp. 37–48.
- Polat, H.; Du, W. SVD-based collaborative filtering with privacy. Proceedings of the ACM International Symposium Applications Computing (SASC), Santa Fe, NM, USA, 13–17 March 2005; pp. 791–795.
- Agrawal, D.; Aggarwal, C.C. On the design and quantification of privacy preserving data mining algorithms. Proceedings of the ACM SIGMOD International Conference Management Data, Santa Barbara, CA, USA, 21–24 May 2001; pp. 247–255.
- Reiter, M.K.; Rubin, A.D. Crowds: Anonymity for Web transactions. ACM Trans. Inf. Syst. Secur 1998, 1, 66–92. [Google Scholar]
- Chow, C.; Mokbel, M.F.; Liu, X. A peer-to-peer spatial cloaking algorithm for anonymous location-based services. Proceedings of the ACM International Symposium Advances Geographic Information Systems (GIS), Arlington, VA, USA, 10–11 November 2006; pp. 171–178.
- Rebollo-Monedero, D.; Forné, J.; Subirats, L.; Solanas, A.; Martínez-Ballesté, A. A collaborative protocol for private retrieval of location-based information. Proceedings of the IADIS International Conference e-Society, Barcelona, Spain, 25–28 February 2009.
- Rebollo-Monedero, D.; Forné, J. Optimal query forgery for private information retrieval. IEEE Trans. Inf. Theory 2010, 56, 4631–4642. [Google Scholar]
- Parra-Arnau, J.; Rebollo-Monedero, D.; Forné, J. A privacy-preserving architecture for the semantic Web based on tag suppression. Proceedings International Conference Trust, Privacy, Security, Digital Business (TrustBus), Bilbao, Spain, 30 August–3 September 2010; 6264, pp. 58–68.
- Parra-Arnau, J.; Rebollo-Monedero, D.; Forné, J.; Muñoz, J.L.; Esparza, O. Optimal tag suppression for privacy protection in the semantic Web. Data Knowl. Eng 2012, 81–82, 46–66. [Google Scholar]
- Parra-Arnau, J.; Perego, A.; Ferrari, E.; Forné, J.; Rebollo-Monedero, D. Privacy-preserving enhanced collaborative tagging. IEEE Trans. Knowl. Data Eng 2014, 26, 180–193. [Google Scholar]
- Canny, J. Collaborative filtering with privacy via factor analysis. Proceedings of the ACM SIGIR Conference Research Development on Information Retrieval, Tampere, Finland, 11–15 August 2002; pp. 238–245.
- Canny, J.F. Collaborative filtering with privacy. Proceedings of the IEEE Symposium Security, Private (SP), Oakland, CA, USA, 12–15 May 2002; pp. 45–57.
- Ahmad, W.; Khokhar, A. An architecture for privacy preserving collaborative filtering on Web portals. Proceedings of the IEEE International Symposium on Information Assurance and Security, Washington, DC, USA, 29–31 August 2007; pp. 273–278.
- Zhan, J.; Hsieh, C.L.; Wang, I.C.; Hsu, T.S.; Liau, C.J.; Wang, D.W. Privacy-preserving collaborative recommender systems. IEEE Trans. Syst. Man Cybern 2010, 40, 472–476. [Google Scholar]
- Deng, M. Privacy preserving content protection. Ph.D. Dissertation, Katholieke University, Leuven, Belgium, June 2010. [Google Scholar]
- Cottrell, L. Mixmaster and remailer attacks, 1994. Available online: http://obscura.com/~loki/remailer/remailer-essay.html accessed on 9 January 2014.
- Serjantov, A.; Newman, R.E. On the anonymity of timed pool mixes. In Security and Privacy in the Age of Uncertainty, Athens, Greece, Proceedings of the Workshop Private, Anonymous Issues Network, Distribution System, 26–28 May 2003; Springer: New York, NY, USA, 2003; pp. 427–434. [Google Scholar]
- Möller, U.; Cottrell, L.; Palfrader, P.; Sassaman, L. Mixmaster protocol—Version 2. Available online: http://www.freehaven.net/anonbib/cache/mixmaster-spec.txt accessed on 11 December 2013.
- Kesdogan, D.; Egner, J.; Büschkes, R. Stop-and-go mixes: Providing probabilistic anonymity in an open system. Proceedings of the Informationa Hiding Workshop (IH), Portland, OR, USA, 14–17 April 1998; Springer: New York, NY, USA, 1998; pp. 83–98. [Google Scholar]
- Chaum, D. Untraceable electronic mail, return addresses, and digital pseudonyms. Commun. ACM 1981, 24, 84–88. [Google Scholar]
- Rennhard, M.; Plattner, B. Practical anonymity for the masses with mix-networks. Proceedings of the International Workshop Enabling Technology: Infrastructure Collaborative Enterprises (WETICE), Linz, Austria, 9–11 June 2003; pp. 255–260.
- Danezis, G. Mix-networks with restricted routes. Proceedings of the International Symposium Private Enhancing Technology (PETS), Dresden, Germany, 26–28 March 2003; pp. 1–17.
- Goldschlag, D.; Reed, M.; Syverson, P. Hiding routing information. Proceedings of the Information Hiding Workshop (IH), Cambridge, UK, 30 May–1 June 1996; pp. 137–150.
- Reed, M.G.; Syverson, P.F.; Goldschlag, D.M. Proxies for anonymous routing. Proceedings of the Computing Security Application Conference (CSAC), San Diego, CA, USA, 9–13 December 1996; pp. 9–13.
- Dingledine, R.; Mathewson, N.; Syverson, P. Tor: The second-generation onion router. Proceedings of the Conference USENIX Security Symposium, Berkeley, CA, USA, 9–13 August 2004; p. 21.
- Levine, B.N.; Reiter, M.K.; Wang, C.; Wright, M. Timing attacks in low-latency mix systems. Proceedings of the International Financial Cryptography Conference, San Diego, CA, USA, 9–13 August 2004; Springer: New York, NY, USA, 2004; pp. 251–265. [Google Scholar]
- Bauer, K.; McCoy, D.; Grunwald, D.; Kohno, T.; Sicker, D. Low-resource routing attacks against anonymous systems; Technical Report; University of Colorado: Boulder, CO, USA, 2007. [Google Scholar]
- Murdoch, S.J.; Danezis, G. Low-cost traffic analysis of tor. Proceedings of the IEEE Symposium Security, Private (SP), Washington, DC, USA, 8–11 May 2005; pp. 183–195.
- Pfitzmann, B.; Pfitzmann, A. How to break the direct RSA implementation of mixes. Proceedings of the Annual International Conference Theory, Application of Cryptographic Techniques (EUROCRYPT), Aarhus, Denmark, 21–24 May 1990; Springer: New York, NY, USA, 1990; pp. 373–381. [Google Scholar]
- U.S. online and mobile privacy perceptions report. 2012. Available online: http://www.truste.com/about-TRUSTe/press-room/newstrustereleasesuscustomerfindingsreport accessed on 9 January 2014.
- Toubiana, V.; Narayanan, A.; Boneh, D.; Nissenbaum, H.; Barocas, S. Adnostic: Privacy preserving targeted advertising. Proceedings of the IEEE Symposium Networks Distribution System Security (SNDSS), San Diego, CA, USA, 28 February–3 March 2010; pp. 1–21.
- Fredrikson, M.; Livshits, B. RePriv: Re-envisioning in-browser privacy. Proceedings of the IEEE Symposium Security, Private (SP), Berkeley, CA, USA, 22–25 May 2011; pp. 131–146.
- Rebollo-Monedero, D.; Forné, J.; Domingo-Ferrer, J. Query profile obfuscation by means of optimal query exchange between users. IEEE Trans. Depend. Secure Comput 2012, 9, 641–654. [Google Scholar]
- Parra-Arnau, J.; Rebollo-Monedero, D.; Forné, J. A privacy-protecting architecture for recommendation systems via the suppression of ratings. Int. J. Security, Appl 2012, 6, 61–80. [Google Scholar]
- Li, N.; Li, T.; Venkatasubramanian, S. t-Closeness: Privacy beyond k-anonymity and l-diversity. Proceedings of the IEEE International Conference Data Engineering (ICDE), Istanbul, Turkey, 15–20 April 2007; pp. 106–115.
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Google adwords display planner, Available online: https://support.google.com/adwords/answer/3056153 accessed on 9 January 2014.
- Google display network, Available online: http://www.google.es/ads/displaynetwork accessed on 9 January 2014.
- Estra da Jiménez, J.A. Implementation of a firefox extension that measures user privacy risk in web search. Master’s Thesis; Technical University of Catalonia: Barcelona, Spanish, 2013. Available online: http://hdl.handle.net/2099.1/19549 accessed on 9 January 2014. [Google Scholar]
- Hoyos, A.F.R. Evaluation of the privacy risk for online search and social tagging systems. Master’s Thesis; Technical University of Catalonia: Barcelona, Spanish, 2013. Available online: http://hdl.handle.net/2099.1/19550 accessed on 9 January 2014. [Google Scholar]
- Ibaraki, T.; Katoh, N. Resource Allocation Problems: Algorithmic Approaches; MIT Press: Cambridge, MA, USA, 1988. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- GroupLens research, Available online: http://www.grouplens.org accessed on 9 January 2014.
- MovieLens 10M data set, Available online: http://www.grouplens.org/system/files/ml-10m-README.html accessed on 24 August 2011.













| Category name | Index 1 | Index 2 |
|---|---|---|
| action | 2 | 15 |
| adventure | 5 | 18 |
| animation | 1 | 16 |
| children’s | 4 | 12 |
| comedy | 8 | 14 |
| crime | 6 | 11 |
| documentary | 19 | 9 |
| drama | 18 | 5 |
| fantasy | 10 | 17 |
| film-noir | 3 | 3 |
| horror | 11 | 4 |
| IMAX | 17 | 19 |
| musical | 15 | 1 |
| mystery | 14 | 8 |
| romance | 16 | 6 |
| sci-fi | 7 | 13 |
| thriller | 9 | 10 |
| war | 13 | 7 |
| western | 12 | 2 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Parra-Arnau, J.; Rebollo-Monedero, D.; Forné, J. Optimal Forgery and Suppression of Ratings for Privacy Enhancement in Recommendation Systems. Entropy 2014, 16, 1586-1631. https://doi.org/10.3390/e16031586
Parra-Arnau J, Rebollo-Monedero D, Forné J. Optimal Forgery and Suppression of Ratings for Privacy Enhancement in Recommendation Systems. Entropy. 2014; 16(3):1586-1631. https://doi.org/10.3390/e16031586
Chicago/Turabian StyleParra-Arnau, Javier, David Rebollo-Monedero, and Jordi Forné. 2014. "Optimal Forgery and Suppression of Ratings for Privacy Enhancement in Recommendation Systems" Entropy 16, no. 3: 1586-1631. https://doi.org/10.3390/e16031586