Numerical Simulation of Entropy Generation with Thermal Radiation on MHD Carreau Nanofluid towards a Shrinking Sheet
Abstract
:1. Introduction
2. Mathematical Formulation
3. Physical Quantities of Interest
4. Numerical Method
5. Entropy Generation Analysis
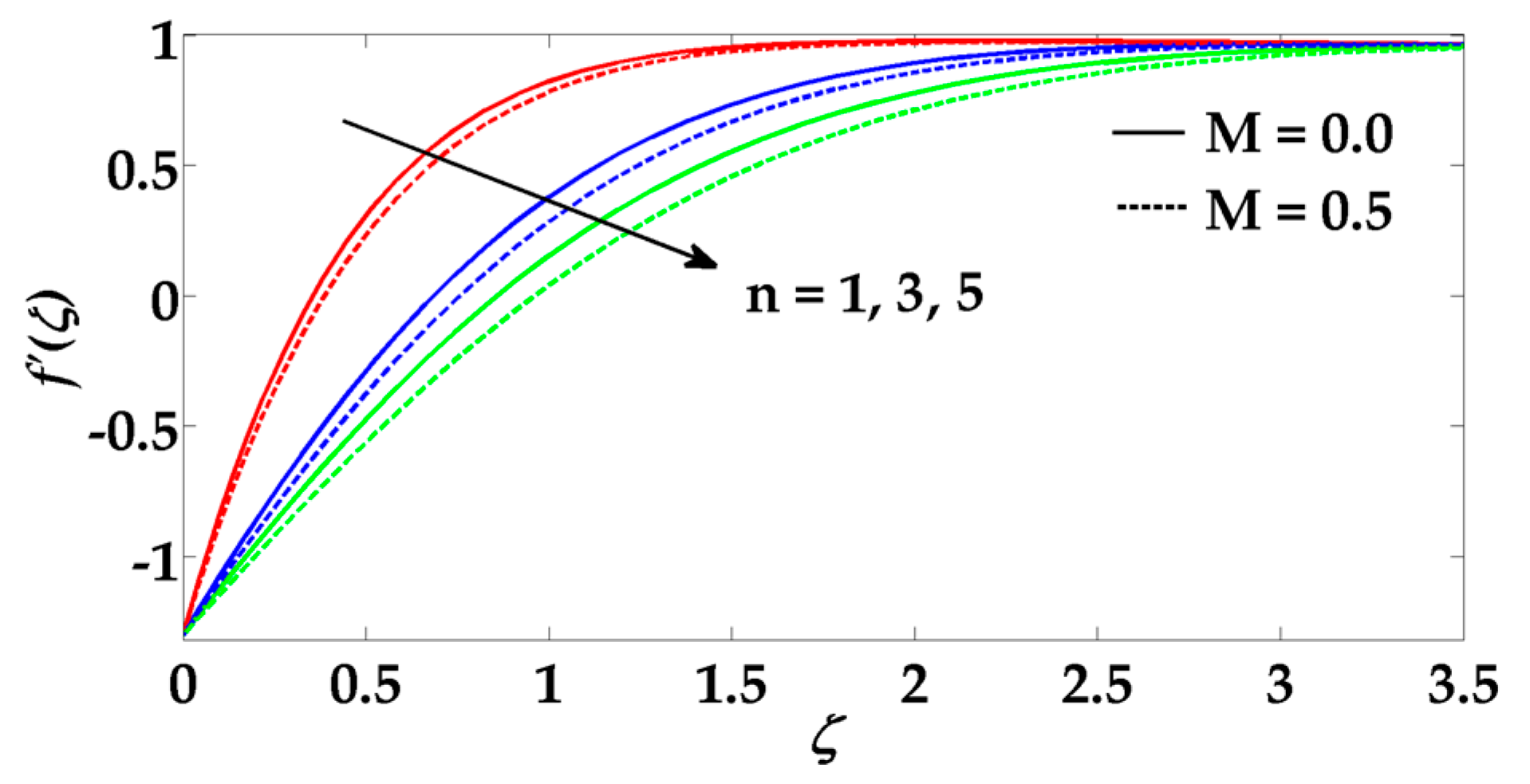
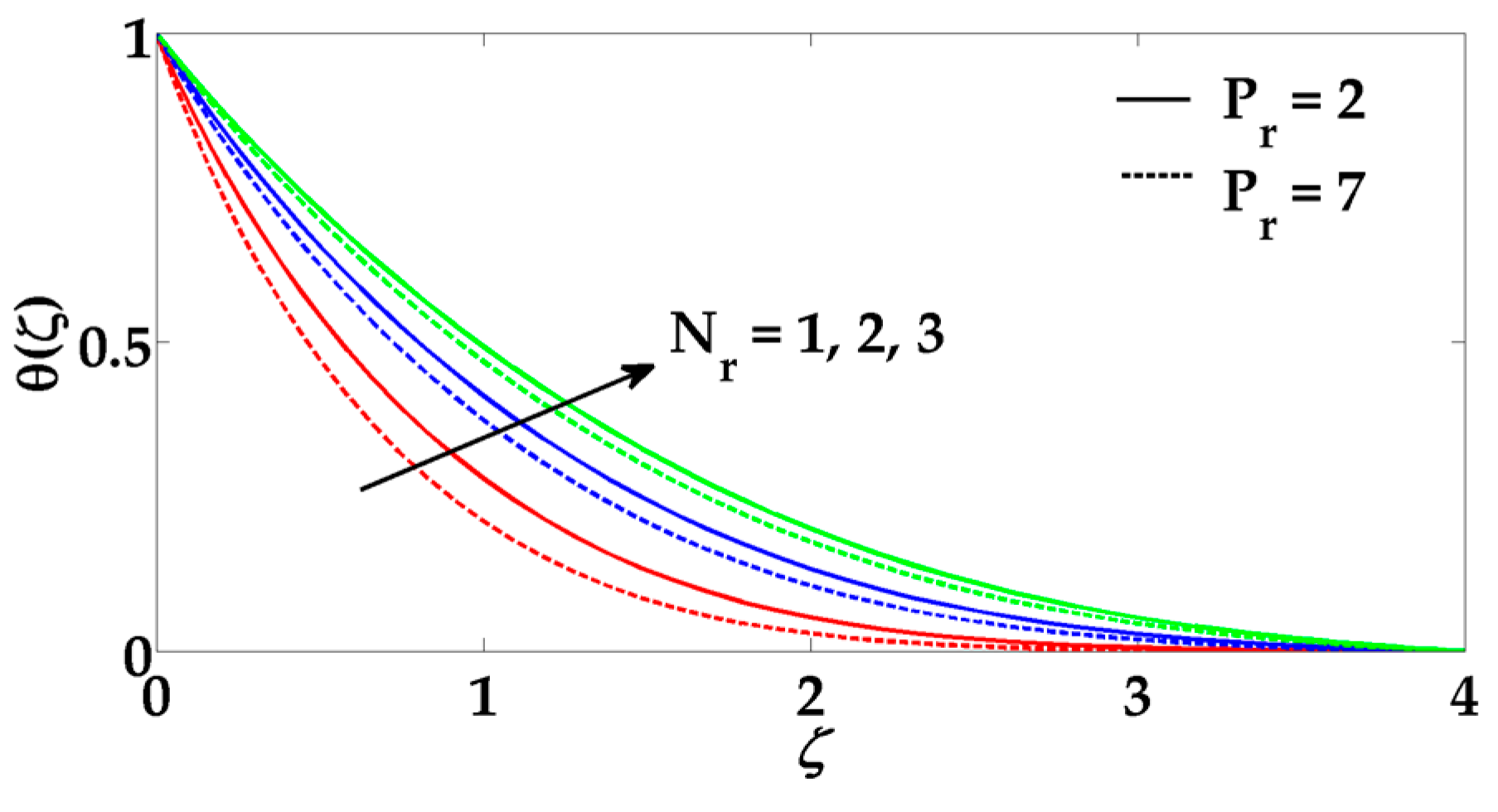
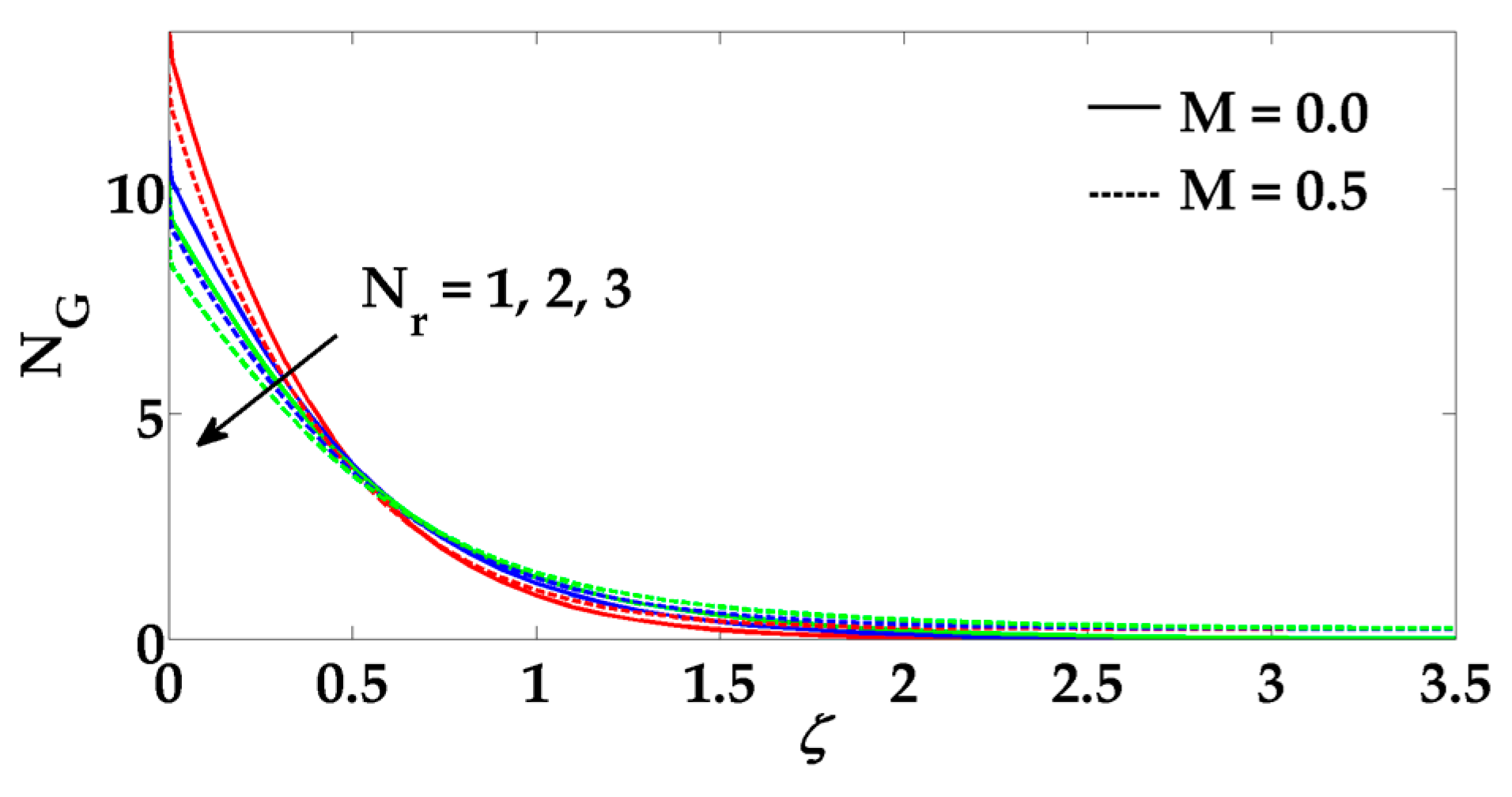
6. Results and Discussions
7. Conclusions
- The magnitude of the velocity decreases for larger values of Hartmann numbers and fluid parameters.
- The Brownian motion parameter and thermophoresis parameter show similar behavior on the temperature profile.
- Larger values of the thermal radiation parameter enhance the temperature profile.
- The concentration profile also behaves as a decreasing function due to the increment in the Lewis number.
- The entropy profile behaves as an increasing function of all the physical parameters of interest.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Velocity components | |
| Cartesian coordinate | |
| Pressure | |
| Power law index | |
| Weissenberg number | |
| Reynolds number | |
| Dimensionless entropy number | |
| Reynolds number | |
| Time | |
| Prandtl number | |
| Mean absorption coefficient | |
| Suction/injection parameter | |
| Brownian motion parameter | |
| Thermophoresis parameter | |
| Heat flux | |
| Lewis number | |
| Mass flux | |
| Brinkman number | |
| Environmental temperature (K) | |
| Hartman number | |
| Magnetic field | |
| Radiation parameter | |
| Temperature and Concentration | |
| Acceleration due to gravity | |
| Brownian diffusion coefficient | |
| Thermophoretic diffusion coefficient |
Greek Symbol
| Thermal conductivity of the nano particles | |
| Stretching parameter | |
| Williamson fluid parameter | |
| Stefan-Boltzmann constant | |
| Viscosity of the fluid | |
| Dimensionless constant parameter | |
| Dimensionless temperature difference | |
| Dimensionless concentration difference | |
| Dimensionless Nanoparticle concentration | |
| Dimensionless Temperature profile | |
| Electrical conductivity | |
| Stream function | |
| Effective heat capacity of nano particle | |
| Nano fluid kinematic viscosity |
References
- Saidur, R.; Leong, K.Y.; Mohammad, H.A. A review on applications and challenges of nanofluids. Renew. Sustain. Energy Rev. 2011, 15, 1646–1668. [Google Scholar] [CrossRef]
- Liu, Z.H.; Li, Y.Y. A new frontier of nanofluid research–application of nanofluids in heat pipes. Int. J. Heat Mass Transf. 2012, 55, 6786–6797. [Google Scholar] [CrossRef]
- Akbar, N.S.; Khan, Z.H. Magnetic field analysis in a suspension of gyrotactic microorganisms and nanoparticles over a stretching surface. J. Magn. Magn. Mater. 2016, 410, 72–80. [Google Scholar] [CrossRef]
- Hayat, T.; Imtiaz, M.; Alsaedi, A. Unsteady flow of nanofluid with double stratification and magnetohydrodynamics. Int. J. Heat Mass Transf. 2016, 92, 100–109. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Study of natural convection MHD nanofluid by means of single and multi-walled carbon nanotubes suspended in a salt-water solution. IEEE Trans. Nanotechnol. 2015, 14, 726–734. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A.; Khan, A.A. The shape effects of nanoparticles suspended in HFE-7100 over wedge with entropy generation and mixed convection. Appl. Nanosci. 2015, 1–11. [Google Scholar] [CrossRef]
- Garoosi, F.; Hoseininejad, F.; Rashidi, M.M. Numerical study of heat transfer performance of nanofluids in a heat exchanger. Appl. Thermal Eng. 2016. [Google Scholar] [CrossRef]
- Ali, M.; Zeitoun, O.; Almotairi, S. Natural convection heat transfer inside vertical circular enclosure filled with water-based Al2O3 nanofluids. Int. J. Therm. Sci. 2013, 63, 115–124. [Google Scholar] [CrossRef]
- Ali, M.; Zeitoun, O.; Almotairi, S.; Al-Ansary, H. The effect of Alumina-water nanofluid on natural convection heat transfer inside vertical circular enclosure heated from above. Heat Transf. Eng. 2013, 34, 1289–1299. [Google Scholar] [CrossRef]
- Zeitoun, O.; Ali, M. Nanofluid impingement jet heat transfer. Nanoscale Res. Lett. 2012, 7, 139. [Google Scholar] [CrossRef] [PubMed]
- Zeitoun, O.; Ali, M.; Al-Ansary, H. The effect of particle concentration on cooling of a circular horizontal surface using nanofluid jets. Nanoscale Microscale Thermophys. Eng. 2013, 17, 154–171. [Google Scholar] [CrossRef]
- Ali, M; Zeitoun, O. Nanofluids forced convection heat transfer inside circular tubes. Int. J. Nanopart. 2009, 2, 164–172. [Google Scholar]
- Murshed, S.M.S.; Leong, K.C.; Yang, C. Thermophysical and electrokinetic properties of nanofluids—A critical review. Appl. Thermal Eng. 2008, 28, 2109–2125. [Google Scholar] [CrossRef]
- Scherer, C.; Figueiredo Neto, A.M. Ferrofluids: Properties and applications. Braz. J. Phys. 2005, 35, 718–727. [Google Scholar] [CrossRef]
- Baumgartl, J.; Hubert, A.; Müller, G. The use of magnetohydrodynamic effects to investigate fluid flow in electrically conducting melts. Phys. Fluids A Fluid Dyn. (1989–1993) 1993, 5, 3280–3289. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Keimanesh, M.; Bég, O.A.; Hung, T.K. Magnetohydrodynamic biorheological transport phenomena in a porous medium: A simulation of magnetic blood flow control and filtration. Int. J. Numer. Methods Biomed. Eng. 2011, 27, 805–821. [Google Scholar] [CrossRef]
- Nisar, A.; Afzulpurkar, N.; Mahaisavariya, B.; Tuantranont, A. MEMS-based micropumps in drug delivery and biomedical applications. Sens. Actuators B Chem. 2008, 130, 917–942. [Google Scholar] [CrossRef]
- Mabood, F.; Ibrahim, S.M.; Rashidi, M.M.; Shadloo, M.S.; Lorenzini, G. Non-uniform heat source/sink and Soret effects on MHD non-Darcian convective flow past a stretching sheet in a micropolar fluid with radiation. Int. J. Heat Mass Transf. 2016, 93, 674–682. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Rostami, B.; Freidoonimehr, N.; Abbasbandy, S. Free convective heat and mass transfer for MHD fluid flow over a permeable vertical stretching sheet in the presence of the radiation and buoyancy effects. Ain Shams Eng. J. 2014, 5, 901–912. [Google Scholar] [CrossRef]
- Zeeshan, A.; Majeed, A.; Ellahi, R. Effect of magnetic dipole on viscous ferro-fluid past a stretching surface with thermal radiation. J. Mol. Liq. 2016, 215, 549–554. [Google Scholar] [CrossRef]
- Yasin, M.H.M.; Ishak, A.; Pop, I. MHD heat and mass transfer flow over a permeable stretching/shrinking sheet with radiation effect. J. Magn. Magn. Mater. 2016, 407, 235–240. [Google Scholar] [CrossRef]
- Mabood, F.; Khan, W.A. Analytical study for unsteady nanofluid MHD Flow impinging on heated stretching sheet. J. Mol. Liq. 2016, 219, 216–223. [Google Scholar] [CrossRef]
- Sandeep, N.; Sulochana, C.; Kumar, B.R. Unsteady MHD radiative flow and heat transfer of a dusty nanofluid over an exponentially stretching surface. Eng. Sci. Technol. Int. J. 2016, 19, 227–240. [Google Scholar] [CrossRef]
- Ene, R.D.; Marinca, V. Approximate solutions for steady boundary layer MHD viscous flow and radiative heat transfer over an exponentially porous stretching sheet. Appl. Math. Comput. 2015, 269, 389–401. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Kavyani, N.; Abelman, S. Investigation of entropy generation in MHD and slip flow over a rotating porous disk with variable properties. Int. J. Heat Mass Transf. 2014, 70, 892–917. [Google Scholar] [CrossRef]
- Qing, J.; Bhatti, M.M.; Abbas, M.A.; Rashidi, M.M.; Ali, M.E.-S. Entropy Generation on MHD Casson Nanofluid Flow over a Porous Stretching/Shrinking Surface. Entropy 2016, 18, 1–14. [Google Scholar] [CrossRef]
- Mahmud, S.; Fraser, R.A. Magnetohydrodynamic free convection and entropy generation in a square porous cavity. Int. J. Heat Mass Transf. 2004, 47, 3245–3256. [Google Scholar] [CrossRef]
- Tasnim, S.H.; Shohel, M.; Mamun, M.A.H. Entropy generation in a porous channel with hydromagnetic effect. Exergy 2002, 2, 300–308. [Google Scholar] [CrossRef]
- Butt, A.S.; Ali, A. Entropy effects in hydromagnetic free convection flow past a vertical plate embedded in a porous medium in the presence of thermal radiation. Eur. Phys. J. Plus 2013, 128, 51–65. [Google Scholar] [CrossRef]
- Komurgoz, G.; Arikoglu, A.; Ozkol, I. Analysis of the magnetic effect on entropy generation in an inclined channel partially filled with porous medium. Num. Heat Transf. Part A 2012, 61, 786–799. [Google Scholar] [CrossRef]
- Abbas, M.A.; Bai, Y.; Rashidi, M.M.; Bhatti, M.M. Analysis of Entropy Generation in the Flow of Peristaltic Nanofluids in Channels with Compliant Walls. Entropy 2016, 18, 90. [Google Scholar] [CrossRef]
- Akbar, N.S. Entropy generation analysis for a CNT suspension nanofluid in plumb ducts with peristalsis. Entropy 2015, 17, 1411–1424. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Parsa, A.B.; Bég, O.A.; Shamekhi, L.; Sadri, S.M.; Bég, T.A. Parametric analysis of entropy generation in magneto-hemodynamic flow in a semi-porous channel with OHAM and DTM. Appl. Bion. Biomech. 2014, 11, 47–60. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Bhatti, M.M.; Abbas, M.A.; Ali, M.E.-S. Entropy Generation on MHD Blood Flow of Nanofluid Due to Peristaltic Waves. Entropy 2016, 18, 117. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Pop, I.; Rahman, M.M. Three-dimensional natural convection in a porous enclosure filled with a nanofluid using Buongiorno’s mathematical model. Int. J. Heat Mass Transf. 2015, 82, 396–405. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Pop, I.; Shenoy, A. Unsteady free convection in a porous open wavy cavity filled with a nanofluid using Buongiorno's mathematical model. Int. Commun. Heat Mass Transf. 2015, 67, 66–72. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Pop, I.; Roşca, N.C. Magnetic field effect on the unsteady natural convection in a wavy-walled cavity filled with a nanofluid: Buongiorno’s mathematical model. J. Taiwan Inst. Chem. Eng. 2016, 61, 211–222. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Oztop, H.F.; Pop, I.; Abu-Hamdeh, N. Analysis of Entropy Generation in Natural Convection of Nanofluid inside a Square Cavity Having Hot Solid Block: Tiwari and Das’ Model. Entropy 2015, 18. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Shahid, A.; Rashidi, M.M. Numerical simulation of Fluid flow over a shrinking porous sheet by Successive linearization method. Alex. Eng. J. 2016, 55, 51–56. [Google Scholar] [CrossRef]
- Mahapatra, T.R.; Nandy, S.K. Stability of dual solutions in stagnation-point flow and heat transfer over a porous shrinking sheet with thermal radiation. Meccanica 2013, 48, 23–32. [Google Scholar] [CrossRef]
- Lok, Y.Y.; Amin, N.; Pop, I. Non-orthogonal stagnation point flow towards a stretching sheet. Int. J. Non-Linear Mech. 2006, 41, 622–627. [Google Scholar] [CrossRef]
- Wang, C.Y. Stagnation flow towards a shrinking sheet. Int. J. Non-Linear Mech. 2008, 43, 377–382. [Google Scholar] [CrossRef]








| - | ||||||
| - | - | - | - | 2.1657 | - | |
| - | - | - | - | 2.9205 | - | |
| - | - | - | - | 1.8475 | - | |
| - | - | - | - | - | ||
| - | - | - | - | - | ||
| - | - | - | - | 0.7765 | ||
| - | - | - | - | 1.2441 | ||
| - | - | - | - | 1.4333 | 1.5063 | |
| - | - | - | - | 1.3605 | ||
| - | - | - | - | 0.8944 | ||
| - | - | - | - | 1.4333 | 0.6264 | |
| - | - | - | - | - | 1.5063 | |
| - | - | - | - | - | 1.9470 | |
| - | - | - | - | - | 2.8467 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhatti, M.M.; Abbas, T.; Rashidi, M.M.; Ali, M.E.-S. Numerical Simulation of Entropy Generation with Thermal Radiation on MHD Carreau Nanofluid towards a Shrinking Sheet. Entropy 2016, 18, 200. https://doi.org/10.3390/e18060200
Bhatti MM, Abbas T, Rashidi MM, Ali ME-S. Numerical Simulation of Entropy Generation with Thermal Radiation on MHD Carreau Nanofluid towards a Shrinking Sheet. Entropy. 2016; 18(6):200. https://doi.org/10.3390/e18060200
Chicago/Turabian StyleBhatti, Muhammad Mubashir, Tehseen Abbas, Mohammad Mehdi Rashidi, and Mohamed El-Sayed Ali. 2016. "Numerical Simulation of Entropy Generation with Thermal Radiation on MHD Carreau Nanofluid towards a Shrinking Sheet" Entropy 18, no. 6: 200. https://doi.org/10.3390/e18060200








