Analysis of Entropy Generation in Flow of Methanol-Based Nanofluid in a Sinusoidal Wavy Channel
Abstract
:1. Introduction
2. Problem Formulation
3. Entropy Generation Analysis
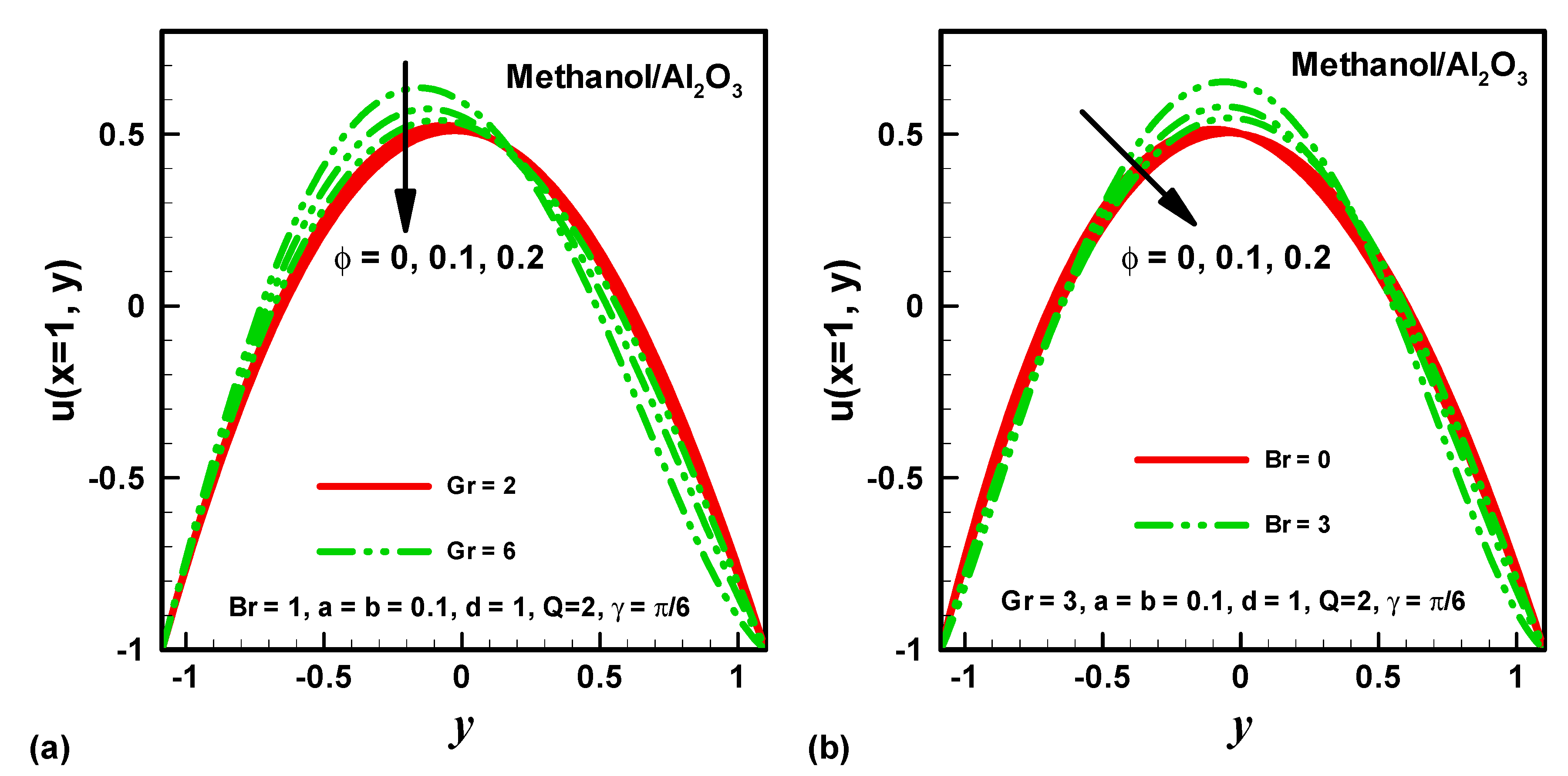
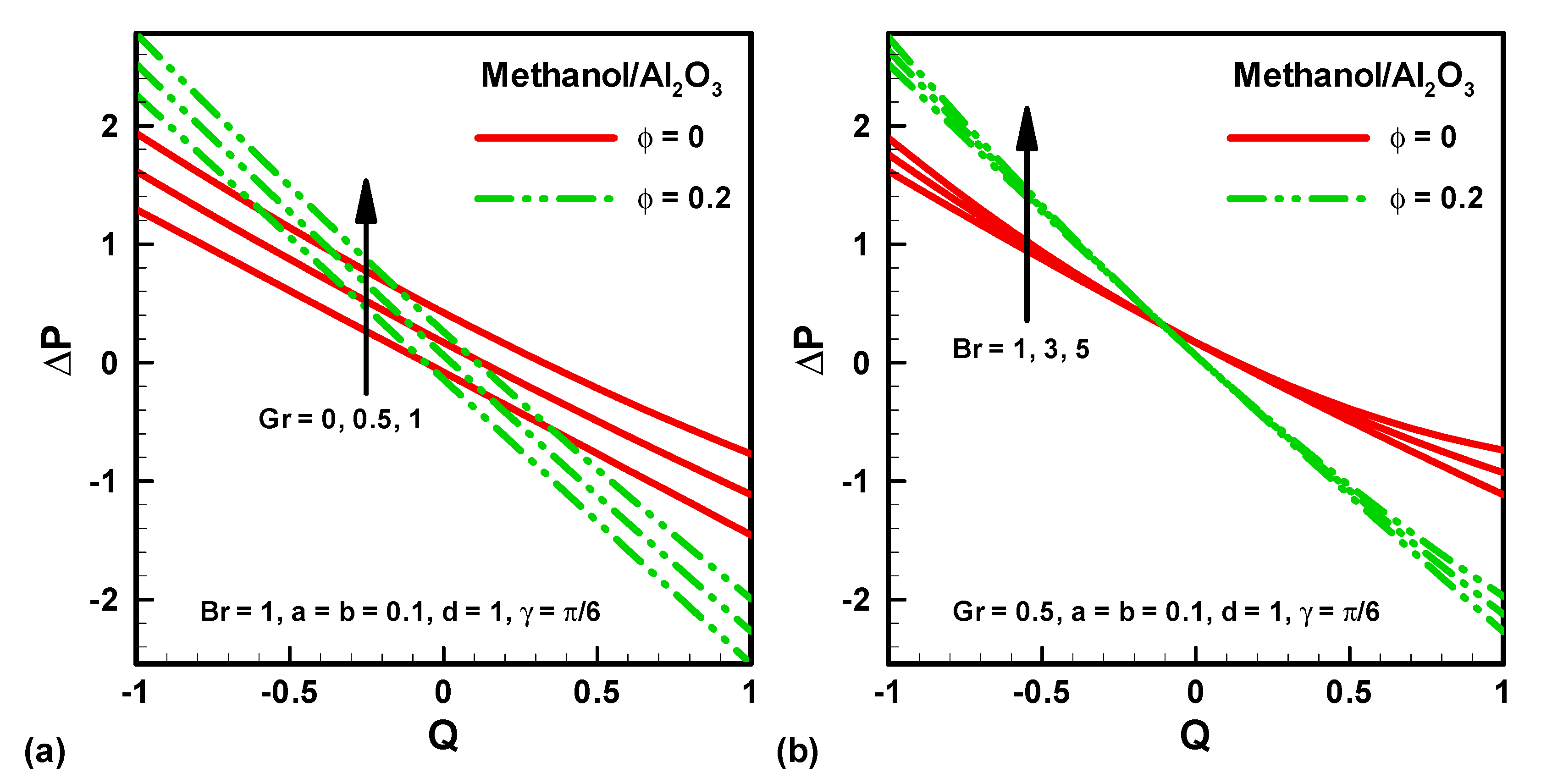
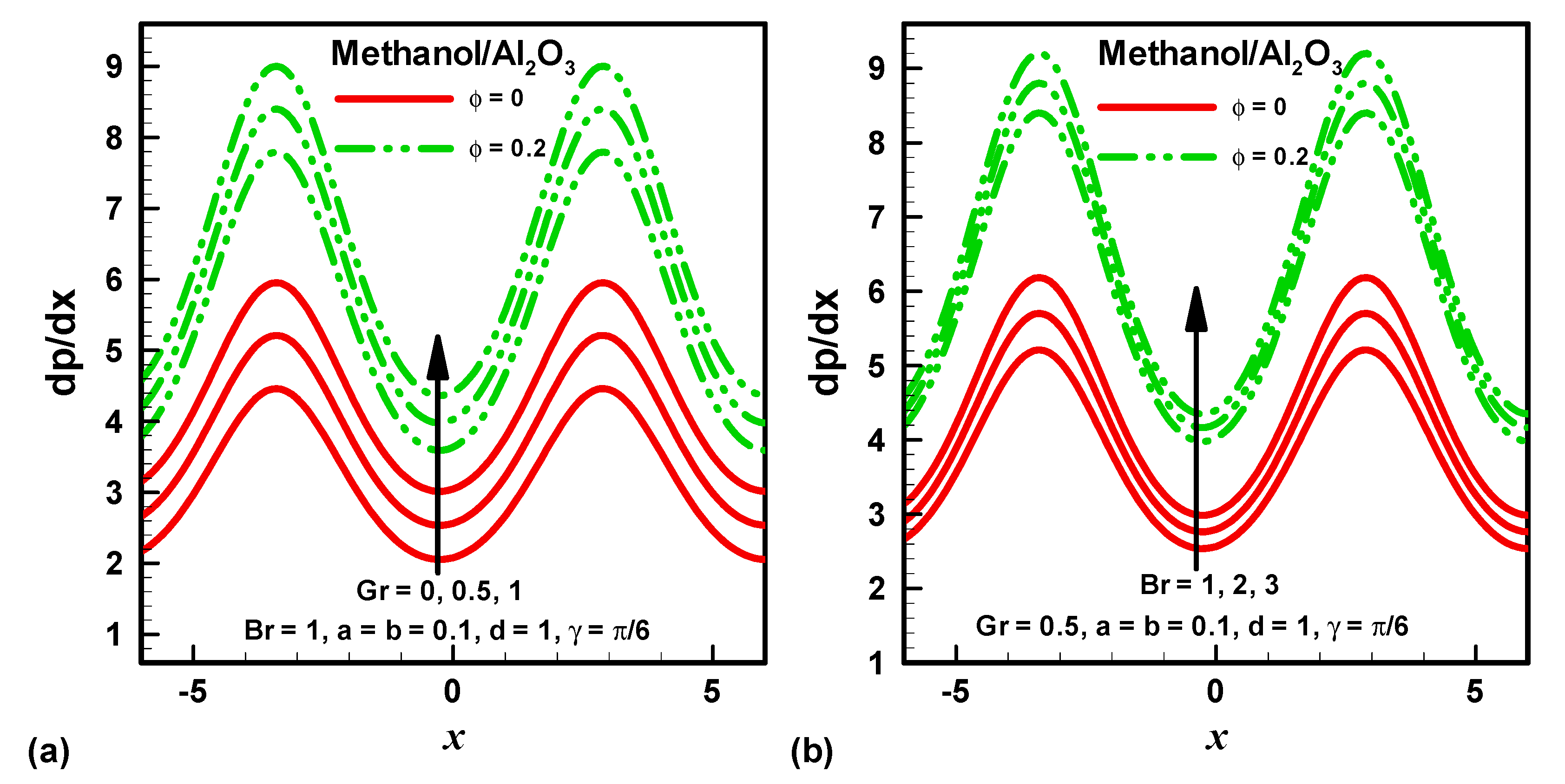
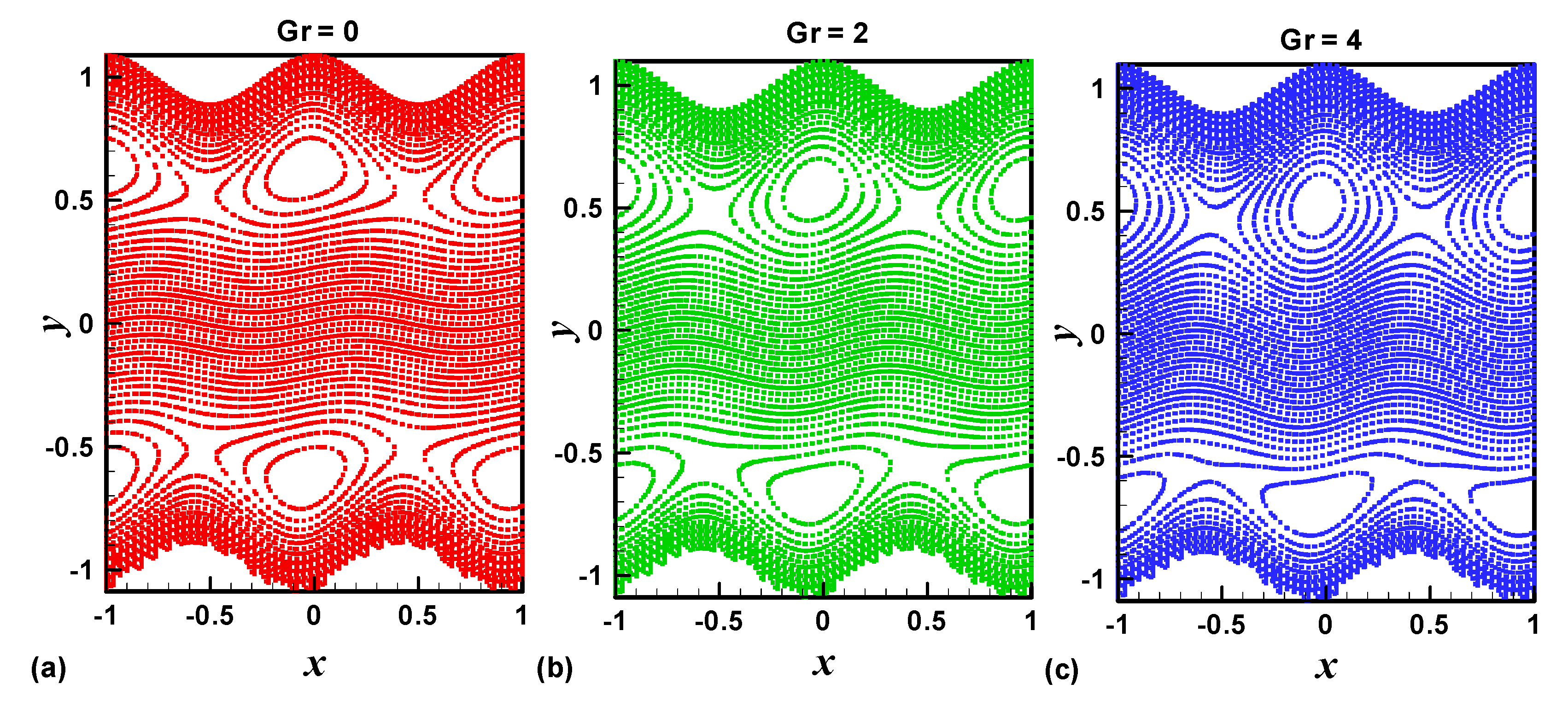
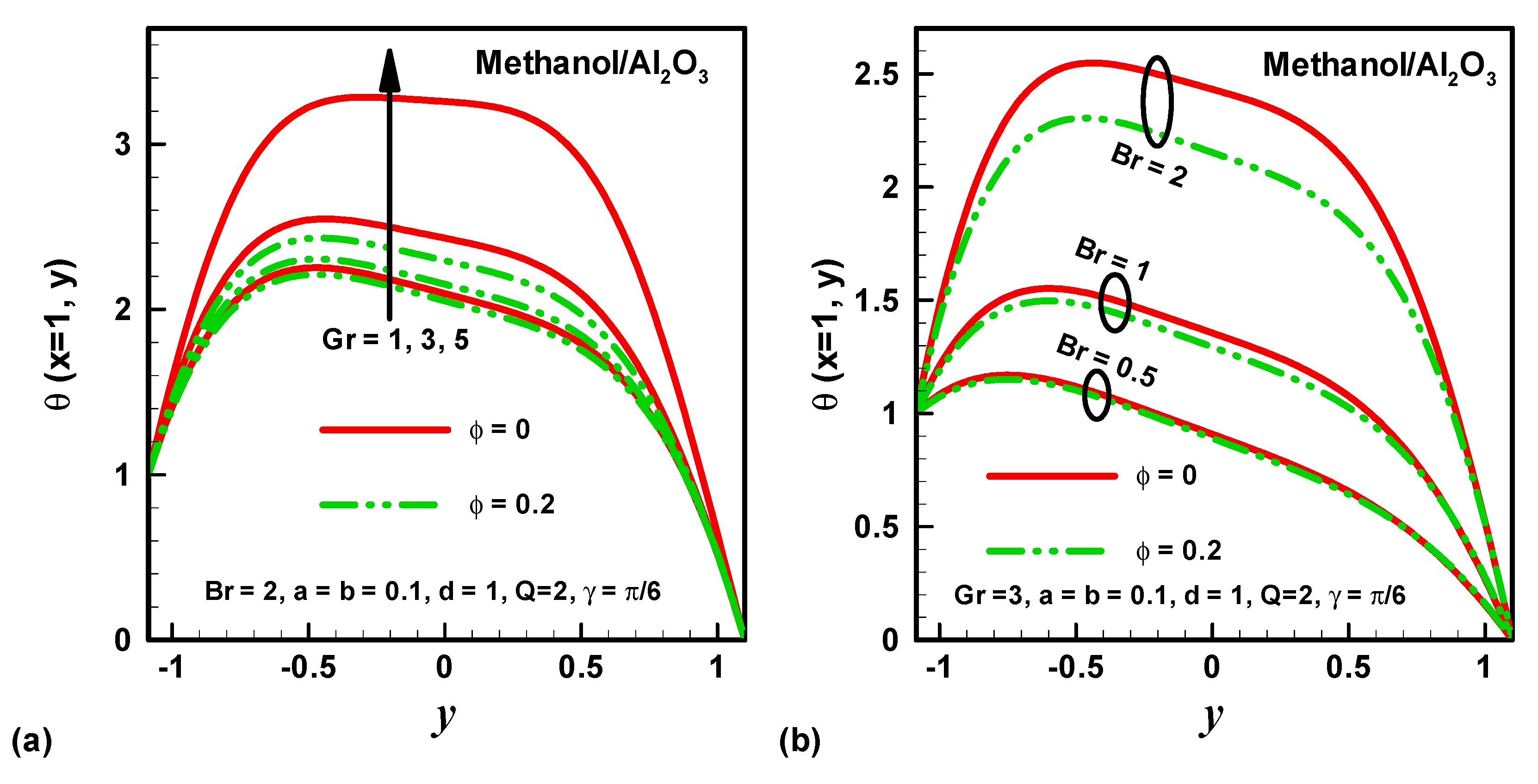
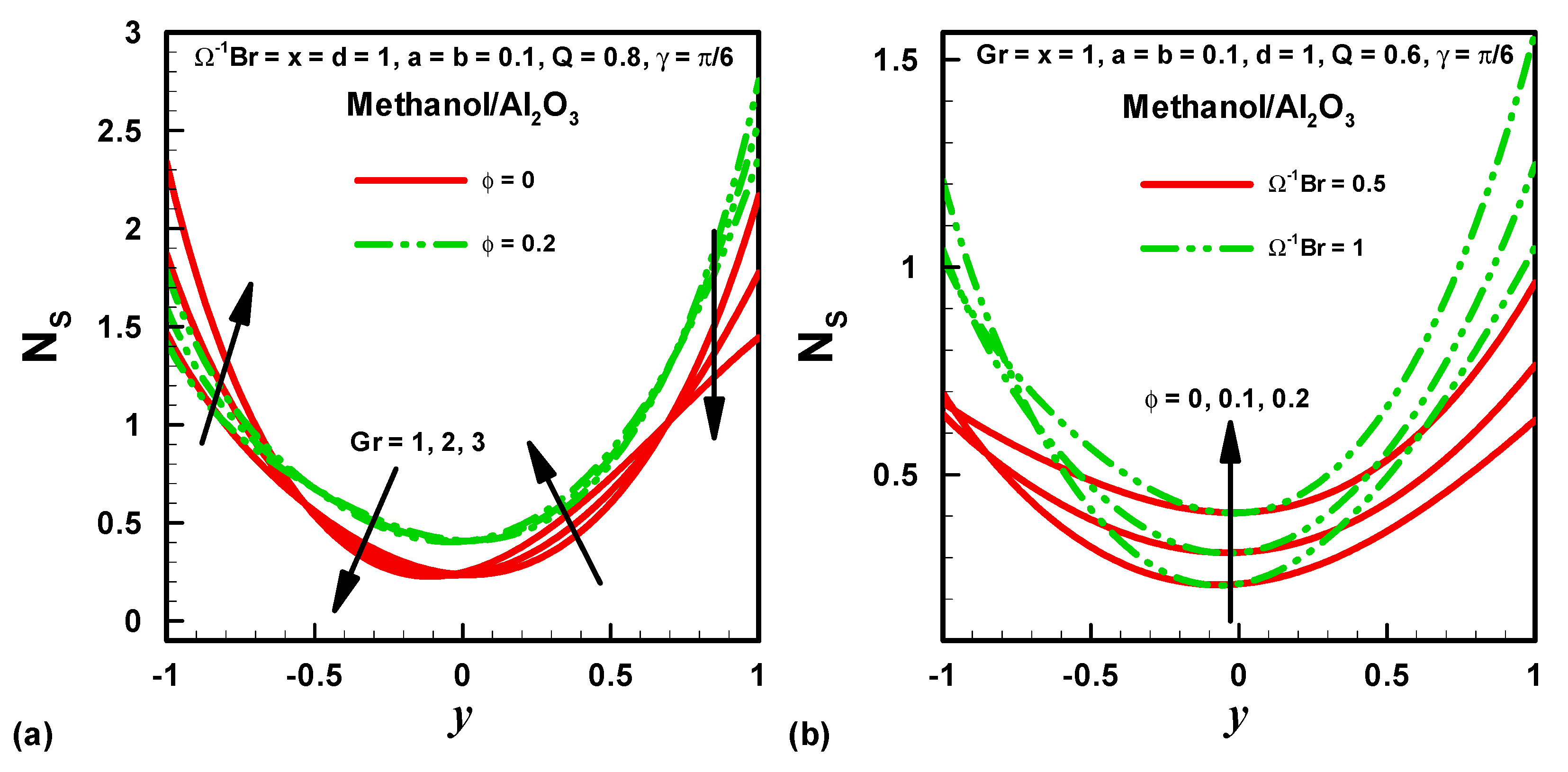
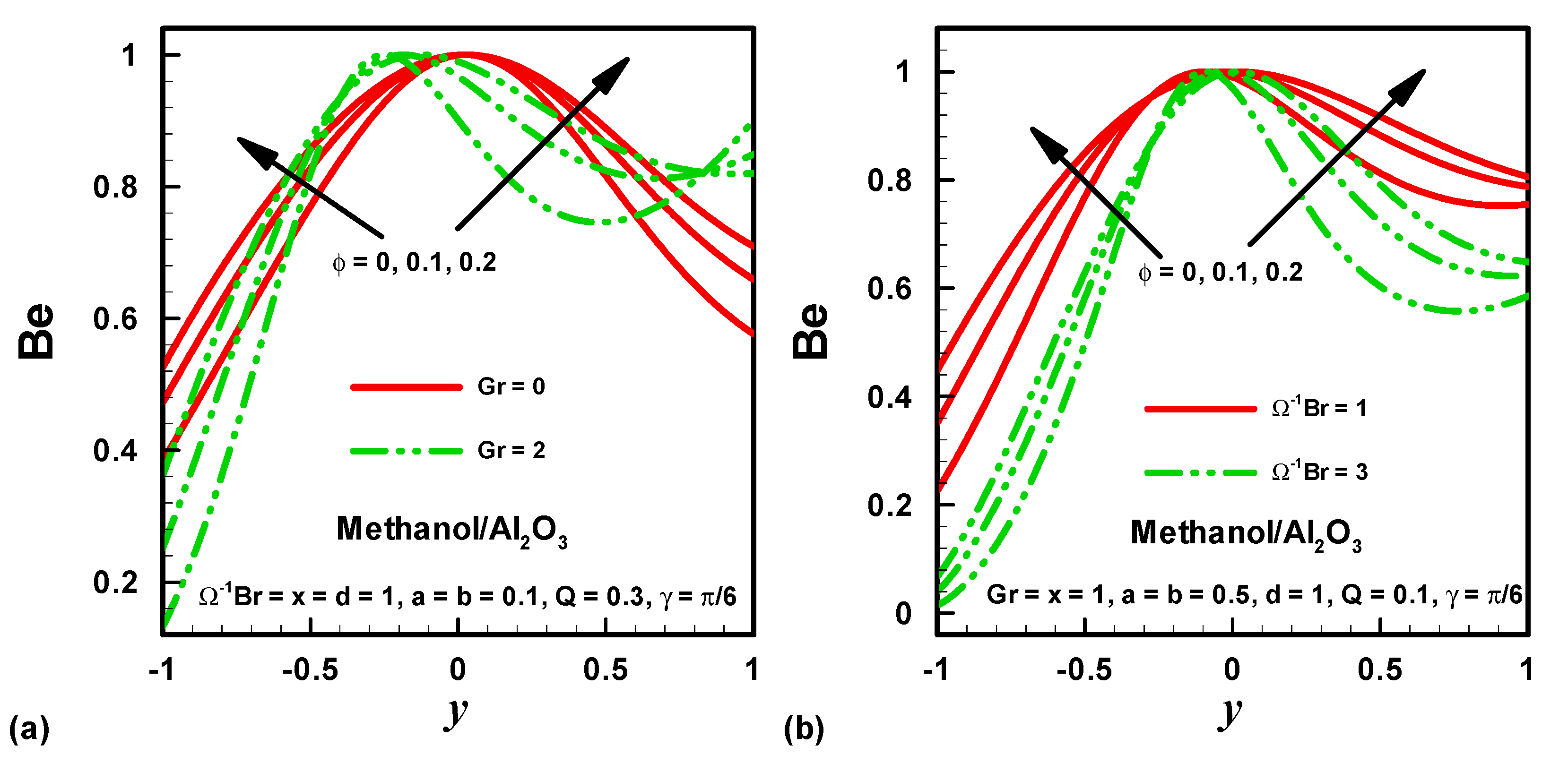
4. Results and Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Latham, T.W. Fluid Motion in a Peristaltic Pump. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1966. [Google Scholar]
- Shapiro, A.H.; Jaffrin, M.Y.; Weinberg, S.L. Peristaltic pumping with long wave lengths at low Reynolds numbers. J. Fluid Mech. 1969, 37, 799–825. [Google Scholar] [CrossRef]
- Mekheimer, K.S. Peristaltic flow of blood under the effect of magnetic field in a non-uniform channels. Appl. Math. Comput. 2004, 153, 763–777. [Google Scholar] [CrossRef]
- Mekheimer, Kh.S.; Elmaboud, Y.A. The influence and heat transfer and magnetic field on peristaltic transport of a magnetic field on peristaltic transport of Newtonian fluid in a vertical annulus: Application of an endoscope. Phys. Lett. A 2008, 372, 1657–1665. [Google Scholar] [CrossRef]
- Srinivas, S.; Kothandapani, M. Peristaltic transport in an asymmetric channel with heat transfer-A note. Int. Commun. Heat Mass Transf. 2008, 35, 514–522. [Google Scholar] [CrossRef]
- Kothandapani, M.; Srinivas, S. Peristaltic transport of a Jeffrey fluid under the effect of magnetic field in an asymmetric channel. Int. J. Non-Linear Mech. 2008, 43, 915–924. [Google Scholar] [CrossRef]
- Srinivas, S.; Muthuraj, R. Effects of chemical reaction and space porosity on MHD mixed convective flow in a vertical asymmetric channel with peristalsis. Math. Comput. Model. 2011, 54, 1213–1227. [Google Scholar] [CrossRef]
- Noreen, S.; Hayat, T.; Alsaedi, A. Magnetohydrodynamic peristaltic flow of a pseudoplastic fluid in a curved channel. Zeitschrift Naturforschung A 2010, 29, 387–394. [Google Scholar] [CrossRef]
- Srinivas, S.; Gayathri, R.; Kothandapani, M. Mixed convective heat and mass transfer in an asymmetric channel with peristalsis. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1845–1862. [Google Scholar] [CrossRef]
- Akbar, N.S.; Nadeem, S.; Lee, C. Peristaltic flow of a Prandtl fluid model in an asymmetric channel. Int. J. Phys. Sci. 2012, 7, 687–695. [Google Scholar]
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the 1995 ASME International Mechanical Engineering Congress and Exposition, San Francisco, CA, USA, 12–17 November 1995; pp. 99–105. [Google Scholar]
- Minkowycz, W.J.; Sparrow, E.M.; Abraham, J.P. Nanoparticle Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Akbar, N.S.; Nadeem, S. Endoscopic effects on peristaltic flow of a nanofluid. Commun. Theor. Phys. 2011, 56, 761–768. [Google Scholar] [CrossRef]
- Akbar, N.S.; Nadeem, S.; Hayat, T.; Hendi, A.A. Peristaltic flow of a nanofluid with slip effects. Meccanica 2012, 47, 1283–1294. [Google Scholar] [CrossRef]
- Akbar, N.S.; Nadeem, S. Peristaltic flow of a nanofluid in a non-uniform tube. Heat Mass Transf. 2012, 48, 451–459. [Google Scholar] [CrossRef]
- Shehzad, S.A.; Abbasi, F.M.; Hayat, T.; Alsaadi, F. Model and comparative study for peristaltic transport of water based nanofluids. J. Mol. Liq. 2015, 209, 723–728. [Google Scholar] [CrossRef]
- Tripathi, D.; Anwar Bég, O. Mathematical modelling of peristaltic transport of nanofluids. Int. J. Heat Mass Transf. 2014, 70, 61–70. [Google Scholar] [CrossRef]
- Anwar Bég, O.; Tripathi, D. Mathematica simulation of peristaltic pumping with double-diffusive convection in nanofluids: A bio-nano-engineering model. Proc. Inst. Mech. Eng. Part N 2012, 225, 99–114. [Google Scholar]
- Akbar, N.S. Heat transfer and carbon nano tubes analysis for the peristaltic flow in a diverging tube. Meccanica 2015, 50, 39–47. [Google Scholar] [CrossRef]
- Akbar, N.S.; Khan, Z.H. Metachoronical beating of cilia for nanofluid with Newtonian heating. J. Magn. Magn. Mater. 2015, 381, 235–242. [Google Scholar] [CrossRef]
- Noreen, S.; Qasim, M.; Khan, Z.H. MHD pressure driven flow of nanofluid in curved channel. J. Magn. Magn. Mater. 2015, 393, 490–497. [Google Scholar] [CrossRef]
- Ebaid, A.; Aly, E.H. Exact Analytical Solution of the Peristaltic Nanofluids Flow in an Asymmetric Channel with Flexible Walls and Slip Condition: Application to the Cancer Treatment. Comput. Math. Methods Med. 2013, 8, 825376. [Google Scholar] [CrossRef] [PubMed]
- Naterer, G.F.; Camberos, J.A. Entropy Based Design and Analysis of Fluids Engineering Systems; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Bejan, A. Entropy Generation through Heat and Fluid Flow; Willey: New York, NY, USA, 1982. [Google Scholar]
- Bejan, A. Entropy Generation Minimization; CRC Press: New York, NY, USA, 1996. [Google Scholar]
- Makinde, D.; Osalusi, E. Second law analysis of laminar flow in a channel filled with saturated porous media. Entropy 2005, 7, 148–160. [Google Scholar] [CrossRef]
- Makinde, D. Entropy generation analysis for variable viscosity channel flow with non-uniform wall temperature. Appl. Energy 2008, 85, 384–393. [Google Scholar] [CrossRef]
- Makinde, D.; Eegunjobi, A.S.; Tshehla, M.S. Thermodynamics analysis of variable viscosity Hydromagnetic Couette flow in a rotating system with Hall effects. Entropy 2015, 17, 7811–7826. [Google Scholar] [CrossRef]
- Golra, R.S.R. Second law analysis of mixed convection in a laminar, non-Newtonian fluid flow through a vertical channel. ISRN Appl. Math. 2011, 2011, 287691. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Mohmud, S.; Freidoonimehr, N.; Rostami, B. Analysis of entropy generation in an MHD flow over a rotating porous disk with variable physical properties. Int. J. Exergy 2015, 16, 481–503. [Google Scholar] [CrossRef]
- Arikodlu, A.; Ozkol, I.; Komurgoz, G. Effects of slip on entropy generation in a single rotating disk in MHD flow. Appl. Energy 2008, 85, 1225–1236. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M.; Khan, I.; Sharidan, S.; Alshomrani, A.S. Entropy generation in magnetohydrodynamic mixed convection flow over an inclined stretching sheet. Entropy 2017, 19, 10. [Google Scholar] [CrossRef]
- Khan, A.; Khan, I.; Ali, F.; Shafie, S. A note on entropy generation in MHD flow over a vertical plate embedded in a porous medium with arbitrary shear stress and ramped temperature. J. Porous Media 2016, 19, 175–187. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Abelman, S.; Mehr, N.F. Entropy generation in steady MHD flow due to a rotating porous disk in a nanofluid. Int. J. Heat Mass Transf. 2013, 62, 515–525. [Google Scholar] [CrossRef]
- Souidi, F.; Ayachi, K.; Benyahia, N. Entropy generation rate for peristaltic pump. J. Non-Equilib. Thermodyn. 2009, 34, 171–194. [Google Scholar] [CrossRef]
- Akbar, N.S. Entropy generation analysis for a CNT suspension nanofluid in plumb ducts with peristalsis. Entropy 2015, 17, 1411–1424. [Google Scholar] [CrossRef]
- Akbar, N.S.; Raza, M. Peristaltic flow with thermal conductivity of H2O + Cu nanofluid and entropy generation. Results Phys. 2015, 5, 115–124. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Bhatti, M.M.; Abbas, M.A.; Ali, M.E.S. Entropy generation on MHD blood flow of nanofluid due to peristaltic waves. Entropy 2016, 18, 117. [Google Scholar] [CrossRef]
- Abbas, M.A.; Bai, Y.; Rashidi, M.M.; Bhatti, M.M. Analysis of entropy generation in the flow of peristaltic nanofluids in channels with compliant walls. Entropy 2016, 18, 90. [Google Scholar] [CrossRef]
- Hsiao, K.L. Stagnation electrical MHD nanofluid mixed convection with slip boundary on a stretching Sheet. Appl. Therm Eng. 2016, 98, 850–861. [Google Scholar] [CrossRef]
- Hsiao, K.-L. MHD mixed convection of viscoelastic fluid over a stretching sheet with ohmic dissipation. J. Mech. 2008, 24, 29–34. [Google Scholar] [CrossRef]
- Hsiao, K.L. Numerical solution for Ohmic Soret-Dufour heat and mass mixed convection of viscoelastic fluid over a stretching sheet with multimedia physical features. J. Aerosp. Eng. 2016, 30. [Google Scholar] [CrossRef]
- Hayat, T.; Ahmed, B.; Abbasi, F.M.; Ahmad, B. Mixed convective peristaltic flow of carbon nanotubes submerged in water using different thermal conductivity models. Comput. Methods Programs Biomed. 2016, 135, 141–150. [Google Scholar] [CrossRef] [PubMed]
- Noreen, S.; Rashidi, M.M.; Qasim, M. Blood flow analysis with considering nanofluid effects in vertical channel. Appl. Nanosci. 2017, 7, 193–199. [Google Scholar] [CrossRef]
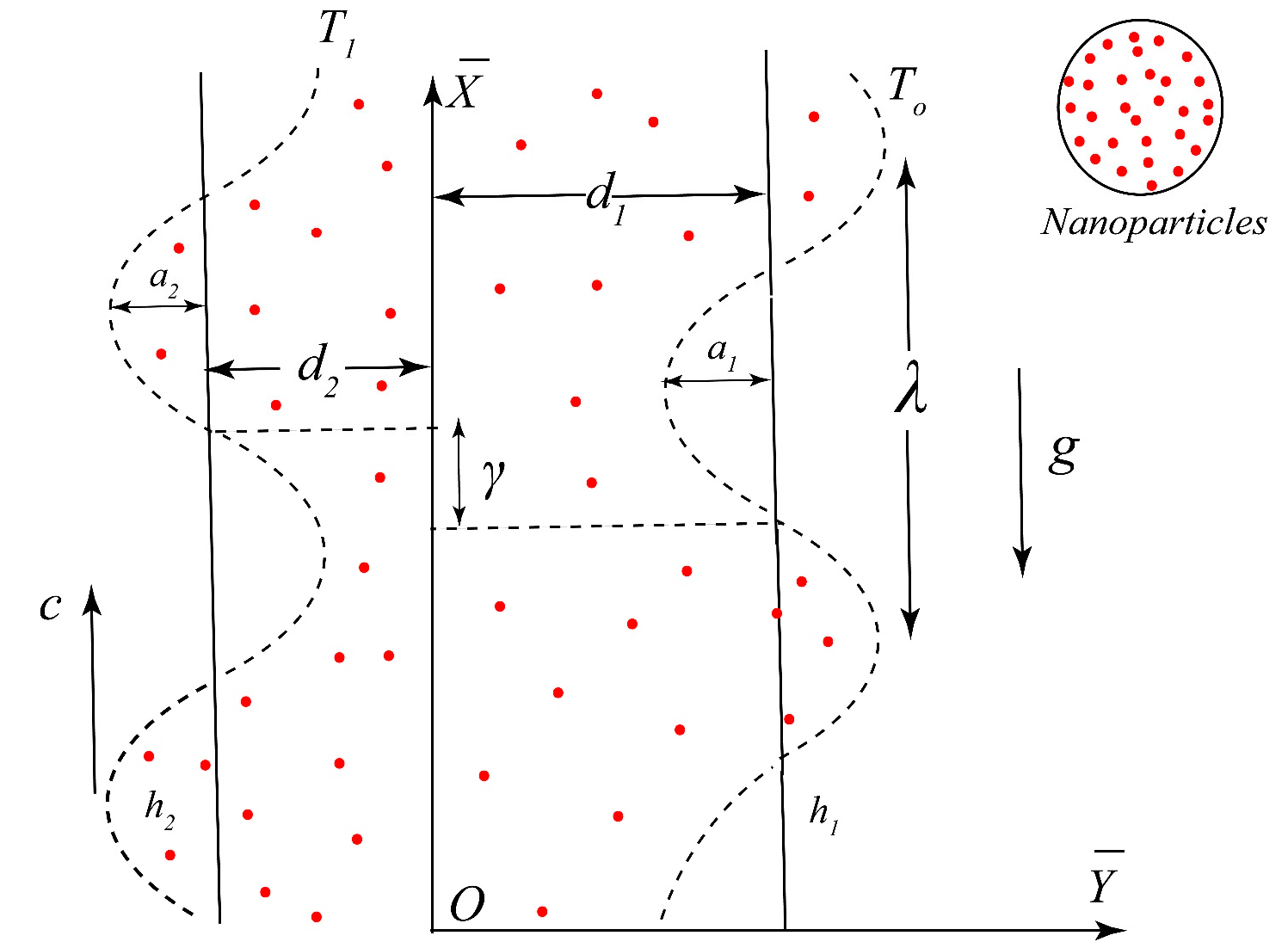
| Physical Properties | Base Fluid | Nanoparticles |
|---|---|---|
| Methanol | Al2O3 | |
| 792 | 3970 | |
| 2545 | 765 | |
| 0.2035 | 40 |
| 0.5 | 0.69963 | 0.69366 | 0.68781 | 0.54627 | 0.55576 | 0.56547 |
| 1 | 1.22518 | 1.21324 | 1.20158 | 1.36309 | 1.38209 | 1.40161 |
| 2 | 2.27628 | 2.25248 | 2.22945 | 2.99672 | 3.03494 | 3.07455 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qasim, M.; Hayat Khan, Z.; Khan, I.; Al-Mdallal, Q.M. Analysis of Entropy Generation in Flow of Methanol-Based Nanofluid in a Sinusoidal Wavy Channel. Entropy 2017, 19, 490. https://doi.org/10.3390/e19100490
Qasim M, Hayat Khan Z, Khan I, Al-Mdallal QM. Analysis of Entropy Generation in Flow of Methanol-Based Nanofluid in a Sinusoidal Wavy Channel. Entropy. 2017; 19(10):490. https://doi.org/10.3390/e19100490
Chicago/Turabian StyleQasim, Muhammad, Zafar Hayat Khan, Ilyas Khan, and Qasem M. Al-Mdallal. 2017. "Analysis of Entropy Generation in Flow of Methanol-Based Nanofluid in a Sinusoidal Wavy Channel" Entropy 19, no. 10: 490. https://doi.org/10.3390/e19100490





