How Can We Fully Use Noiseless Feedback to Enhance the Security of the Broadcast Channel with Confidential Messages

Abstract

The model for a broadcast channel with confidential messages (BC-CM) plays an important role in the physical layer security of modern communication systems. In recent years, it has been shown that a noiseless feedback channel from the legitimate receiver to the transmitter increases the secrecy capacity region of the BC-CM. However, at present, the feedback coding scheme for the BC-CM only focuses on producing secret keys via noiseless feedback, and other usages of the feedback need to be further explored. In this paper, we propose a new feedback coding scheme for the BC-CM. The noiseless feedback in this new scheme is not only used to produce secret keys for the legitimate receiver and the transmitter but is also used to generate update information that allows both receivers (the legitimate receiver and the wiretapper) to improve their channel outputs. From a binary example, we show that this full utilization of noiseless feedback helps to increase the secrecy level of the previous feedback scheme for the BC-CM.

1. Introduction

Wyner, in his outstanding paper on the degraded wiretap channel [1], first studied secure transmission over a physically degraded broadcast channel in the presence of an additional wiretapper. Wyner showed that the secrecy capacity (the maximum transmission rate with perfect secrecy constraint) of the degraded wiretap channel model was given by

$$\begin{array}{c}{C}_s^d=\underset{P\left(x\right)}{max}(I(X;Y)-I(X;Z)),\hfill \end{array}$$

(1)

where X, Y and Z are the channel input, channel output for the legitimate receiver and channel output for the wiretapper, respectively, and they satisfy the Markov chain $X\to Y\to Z$. Note here that the secrecy capacity defined in (1) can be viewed as the difference between the main channel capacity $I(X;Y)$ (the channel for the transmitter and the legitimate receiver) and the wiretap channel capacity $I(X;Z)$ (the channel for the transmitter and the wiretapper). Later, Csiszar and Korner [2] extended Wyner’s work [1] to a more general case: the broadcast channel with confidential messages (BC-CM), where common and confidential messages were transmitted through a discrete memoryless general broadcast channel (without the degradedness assumption $X\to Y\to Z$), and the common message was intended to be decoded by both the legitimate receiver and the wiretapper, while the confidential message was only allowed to be decoded by the legitimate receiver. The secrecy capacity region (the capacity region with the perfect secrecy constraint) of this generalized model is determined in [2], and it is given by

$$\begin{array}{c}{\mathcal{C}}_s=\{(R_0,R_1):0\le R_0\le min\{I(U;Y),I(U;Z)\}\hfill \\ 0\le R_1\le I(V;Y|U)-I(V;Z|U)\},\hfill \end{array}$$

(2)

where U and V respectively represent the common message and the confidential message, and $R_0$ and $R_1$ are the transmission rates of the common message and the confidential message, respectively. Here note that from (2), it is not difficult to show that the secrecy capacity $C_s$ (the maximum transmission rate of the confidential message with the perfect secrecy constraint) of the BC-CM is given by

$$\begin{array}{c}{C}_s=\underset{P(v,x)}{max}{[I(V;Y)-I(V;Z)]}^{+},\hfill \end{array}$$

(3)

where the function ${\left[x\right]}^{+}=x$ if $x\ge 0$, else ${\left[x\right]}^{+}=0$, and $C_s$ is also called the secrecy capacity of the general wiretap channel. The work of [1] and [2] lays the foundation of the physical layer security in modern communication systems.

Recently, Ahlswede and Cai [3] found that if the legitimate receiver sent his own channel output Y back to the transmitter through a noiseless feedback channel, the secrecy capacity region ${\mathcal{C}}_s$ of the BC-CM could be expanded to an achievable secrecy rate region

$$\begin{array}{c}{\mathcal{C}}_s^{f-cai}=\{(R_0,R_1):0\le R_0\le min\{I(U;Y),I(U;Z)\}\hfill \\ 0\le R_1\le min\{{[I(V;Y|U)-I(V;Z|U)]}^{+}+H\left(Y\right|Z,U,V),I(V;Y|U)\}\},\hfill \end{array}$$

(4)

where the auxiliary random variables U and V are defined similarly as those in (2). The coding scheme of the region ${\mathcal{C}}_s^{f-cai}$ combines Csiszar and Korner’s coding scheme for the BC-CM [2] with the idea of using a secret key to encrypt the transmitted message, where the secret key is generated from the noiseless feedback. Note here that the region ${\mathcal{C}}_s^{f-cai}$ is an inner bound on the secrecy capacity ${\mathcal{C}}_s^f$ of the BC-CM with noiseless feedback, and to the best of the authors’ knowledge, $C_s^f$ remains unknown. Similar to the work of [2], using (4), Ahlswede and Cai also provided an achievable secrecy rate $R_s^{f-cai}$ (lower bound on the secrecy capacity) of the general wiretap channel with noiseless feedback, and it is given by

$$\begin{array}{c}{R}_s^{f-cai}=\underset{P(v,x)}{max}min\{{[I(V;Y)-I(V;Z)]}^{+}+H\left(Y\right|V,Z),I(V;Y)\},\hfill \end{array}$$

(5)

where V is defined in the same way as in (2). In [3], Ahlswede and Cai further pointed out that for the degraded wiretap channel with noiseless feedback (the Markov chain $X\to Y\to Z$ holds), the secrecy capacity $C_s^{df}$ was given by

$$\begin{array}{c}{C}_s^{df}=\underset{P\left(x\right)}{max}min\{I(X;Y)-I(X;Z)+H\left(Y\right|X,Z),I(X;Y)\}.\hfill \end{array}$$

(6)

Here, note that the secrecy capacities in (5) and (6) can be viewed as a combination of two parts: the first part is the difference between the main channel capacity ($I(V;Y)$ or $I(X;Y)$) and the wiretap channel capacity ($I(V;Z)$ or $I(X;Z)$), and the second part is the rate $H\left(Y\right|V,Z)$ ($H\left(Y\right|X,Z)$) of a secret key generated by the noiseless feedback and shared between the legitimate receiver and the transmitter. Comparing (6) with (1) and (5) with (3), it is easy to see that by using the noiseless feedback to generate a secret key encrypting the transmitted message, the secrecy capacity of the wiretap channel can be enhanced. Besides the work of [3], other related works on the BC-CM or wiretap channel in the presence of noiseless feedback are in [4,5,6,7].

In this paper, we re-visit the BC-CM with noiseless feedback investigated by Ahlswede and Cai [3] (see Figure 1), and we propose a new achievable secrecy rate region for this feedback model. The coding scheme for this achievable region combines the previous Ahlswede and Cai’s scheme [3] with the Wyner-Ziv scheme for lossy source coding with side information [8], i.e., compared with Ahlswede and Cai’s scheme, in our new scheme, the noiseless feedback is not only used to produce the secret key but also used to generate an update information that allows the legitimate receiver to improve his channel output. From a binary example, we show that this full utilization of noiseless feedback helps to obtain a larger achievable secrecy rate of the confidential message.

Now the remainder of this paper is organized as follows. Section 2 is about the problem formulation and the main result of this paper. A binary example is provided in Section 3. Final conclusions are presented in Section 4.

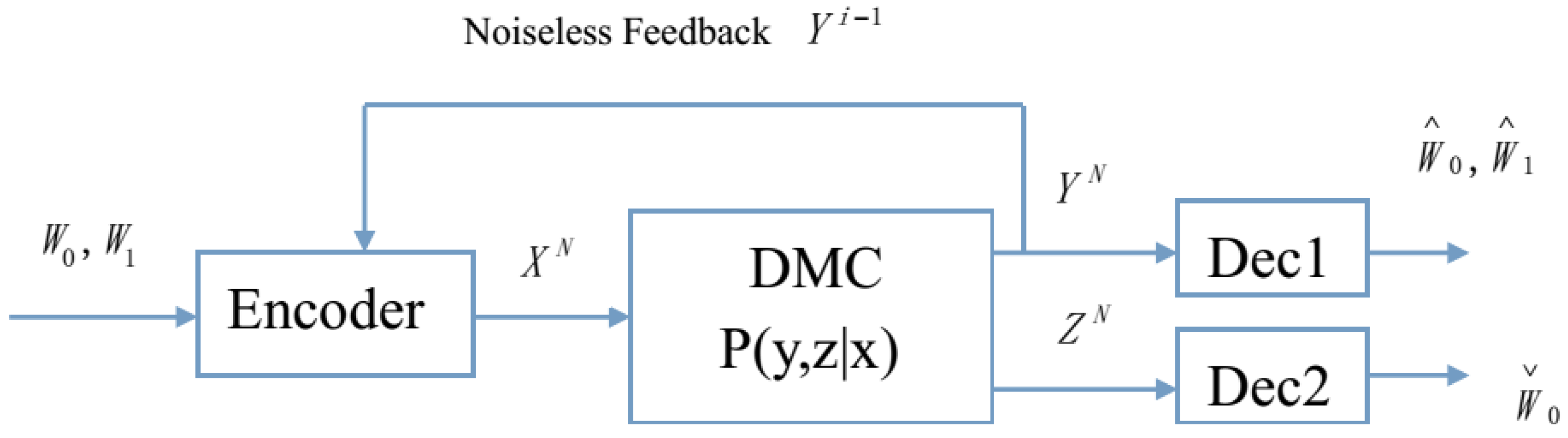
2. Problem Formulation and New Result

Notations: In this paper, random variables are written in upper case letters (e.g. V), real values are written in lower case letters (e.g. v), and members of the alphabet are written in calligraphic letters (e.g. $\mathcal{V}$). Random vectors and their values are written in a similar way. The probability $Pr\{V=v\}$ is shortened to $P\left(v\right)$. In addition, for the remainder of this paper, the base of the logarithm is 2.

Model description: Suppose that the common message $W_0$ is chosen to be transmitted, and it is uniformly distributed over its alphabet ${\mathcal{W}}_0=\{1,2,\dots ,M_0\}$. Analogously, the confidential message $W_1$ is chosen to be transmitted, and it is uniformly distributed over its alphabet ${\mathcal{W}}_1=\{1,2,\dots ,M_1\}$. The channel is discrete and memoryless with input $X^N$, outputs $Y^N$, $Z^N$, and has transition probability $P(y,z|x)$. At time i ($1\le i\le N$), the legitimate receiver receives the channel output $Y_i$, and he sends the previous channel outputs $Y_1$,...,$Y_{i-1}$ back to the transmitter via a noiseless feedback channel. Hence at time i, the channel encoder $f_i$ is denoted by

$$X_i=\left\{\begin{array}{cc}{f}_i(W_0,W_1),\hfill & i=1\hfill \\ f_i(W_0,W_1,Y^{i-1}),\hfill & 2\le i\le N.\hfill \end{array}\right.$$

(7)

Here we should note that $f_i$ does not need to be deterministic and stochastic encoding is also allowed. For the legitimate receiver, after receiving $Y^N$, he uses a decoding mapping ${\psi }_1:{\mathcal{Y}}^N\to {\mathcal{W}}_0\times {\mathcal{W}}_1,$ to obtain ${\widehat{W}}_0$ and ${\widehat{W}}_1$, which are estimations of the transmitted messages $W_0$ and $W_1$, respectively. The legitimate receiver’s decoding error probability $P_{e1}$ is defined by

$$P_{e1}=\frac{1}{M_0{M}_1}\sum _{i=1}^{M_0}\sum _{j=1}^{M_1}Pr\{{\psi }_1\left(y^N\right)\ne (i,j)|(i,j)\mathrm{sent}\}.$$

(8)

For the wiretapper, after receiving $Z^N$, he uses a decoding mapping ${\psi }_2:{\mathcal{Z}}^N\to {\mathcal{W}}_0,$ to obtain ${\check{W}}_0$, which is an estimation of the transmitted message $W_0$. Moreover, the wiretapper also tries to decode the transmitted message $W_1$ via his own channel output $Z^N$, and his equivocation (uncertainty) about $W_1$ is denoted by

$$\Delta =\frac{1}{N}H\left(W_1\right|Z^N).$$

(9)

The wiretapper’s decoding error probability $P_{e2}$ is defined by

$$P_{e2}=\frac{1}{M_0}\sum _{i=1}^{M_0}Pr\{{\psi }_2\left(z^N\right)\ne i|i\mathrm{sent}\}.$$

(10)

Finally, using similar criteria in [1] and [2], if for any small positive number $ϵ$, there exists an encoding-decoding scheme with parameters $M_0$, $M_1$, N, $P_{e1}$ and $P_{e2}$ such that

$$\begin{array}{c}\frac{log{M}_0}{N}\ge R_0-ϵ,\frac{log{M}_1}{N}\ge R_1-ϵ,\Delta \ge R_1-ϵ,P_{e1}\le ϵ,P_{e2}\le ϵ,\hfill \end{array}$$

(11)

we say that the rate pair $(R_0,R_1)$ is achievable with perfect secrecy. The secrecy capacity region $C_s^f$ is composed of all achievable secrecy rate pairs satisfying (5), and the following Theorem 1 provides an inner bound on $C_s^f$.

Theorem 1.

The secrecy capacity region $C_s^f$ of the discrete memoryless BC-CM with noiseless feedback satisfies

$$\begin{array}{c}{C}_s^f\supseteq C_s^{f-new},\hfill \end{array}$$

(12)

where

$$\begin{array}{c}{C}_s^{f-new}=\{(R_0,R_1):0\le R_0\le min\{I(U;Y,V_1),I(U;Z,V_2)\}-I(U,V,Y;V_0,V_2|Z)\hfill \\ 0\le R_1\le min\{{[I(V;Y,V_1|U)-I(V;Z,V_2|U)]}^{+}+H\left(Y\right|Z,U,V,V_2),I(V;Y,V_1|U)\}\hfill \\ 0\le R_0+R_1\le min\{I(U;Y,V_1),I(U;Z,V_2)\}+I(V;Y,V_1|U)-I(V_1;U,V,Y|V_0,Y)\hfill \\ -I(V_2;U,V,Y|V_0,Z)-max\{I(V_0;U,V,Y|Y),I(V_0;U,V,Y|Z)\}\},\hfill \end{array}$$

the joint probability mass function $P(v_0,v_1,v_2,u,v,x,y,z)$ is denoted by

$$\begin{array}{c}P(v_0,v_1,v_2,u,v,x,y,z)=P(v_0,v_1,v_2|u,v,y)P(y,z|x)P\left(x\right|u,v)P\left(v\right|u)P\left(u\right),\hfill \end{array}$$

(13)

and the auxiliary random variables $V_0$, $V_1$, $V_2$, V, U take values in finite alphabets.

Proof. 

The coding scheme for the inner bound $C_s^{f-new}$ combines the previous Ahlswede and Cai’s scheme of the model of Figure 1 with a “generalized” Wyner-Ziv scheme for lossy source coding with side information [8], and the details of the proof of Theorem 1 are in Appendix A. ☐

Remark 1.

There are some notes on Theorem 1; see the following.

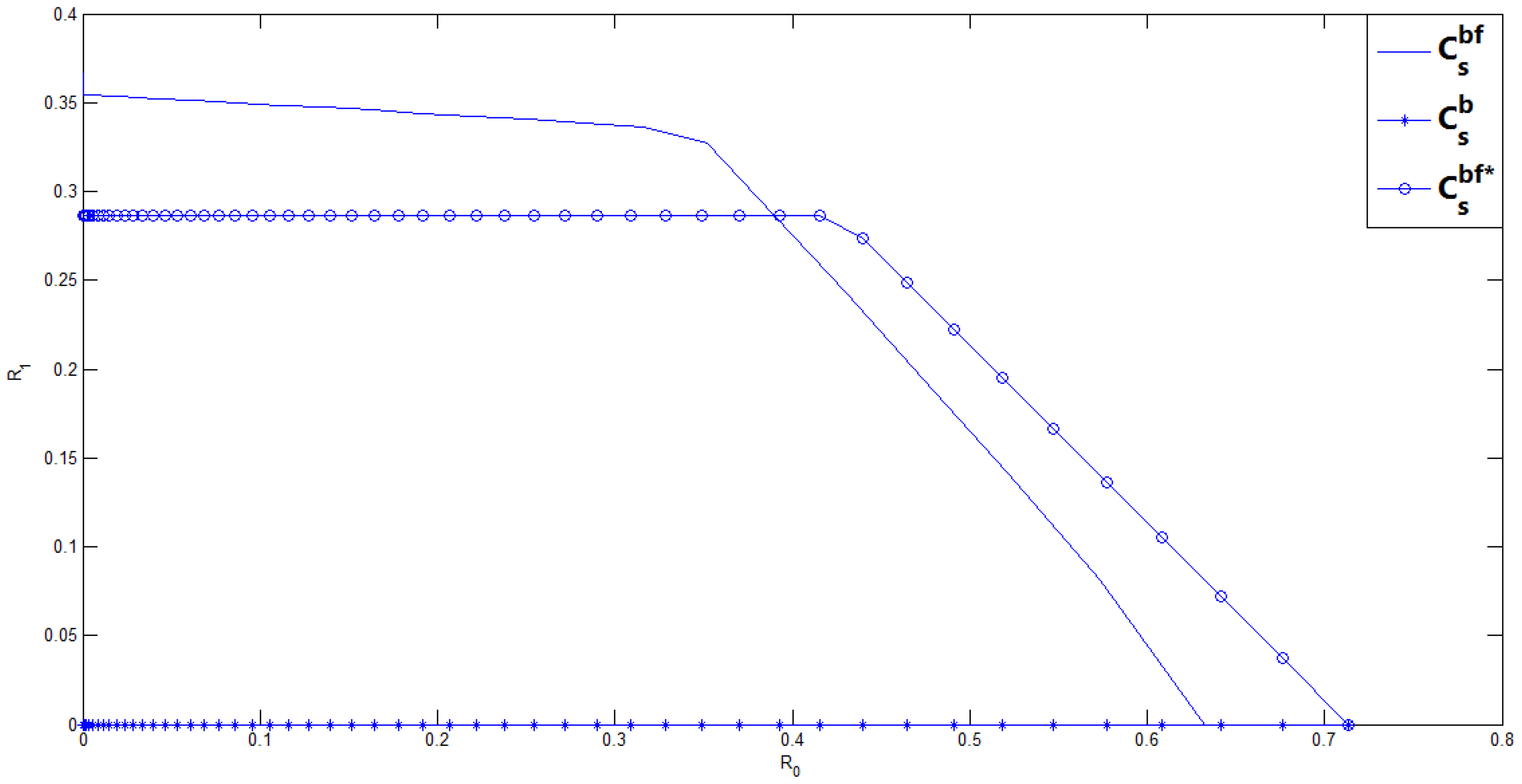
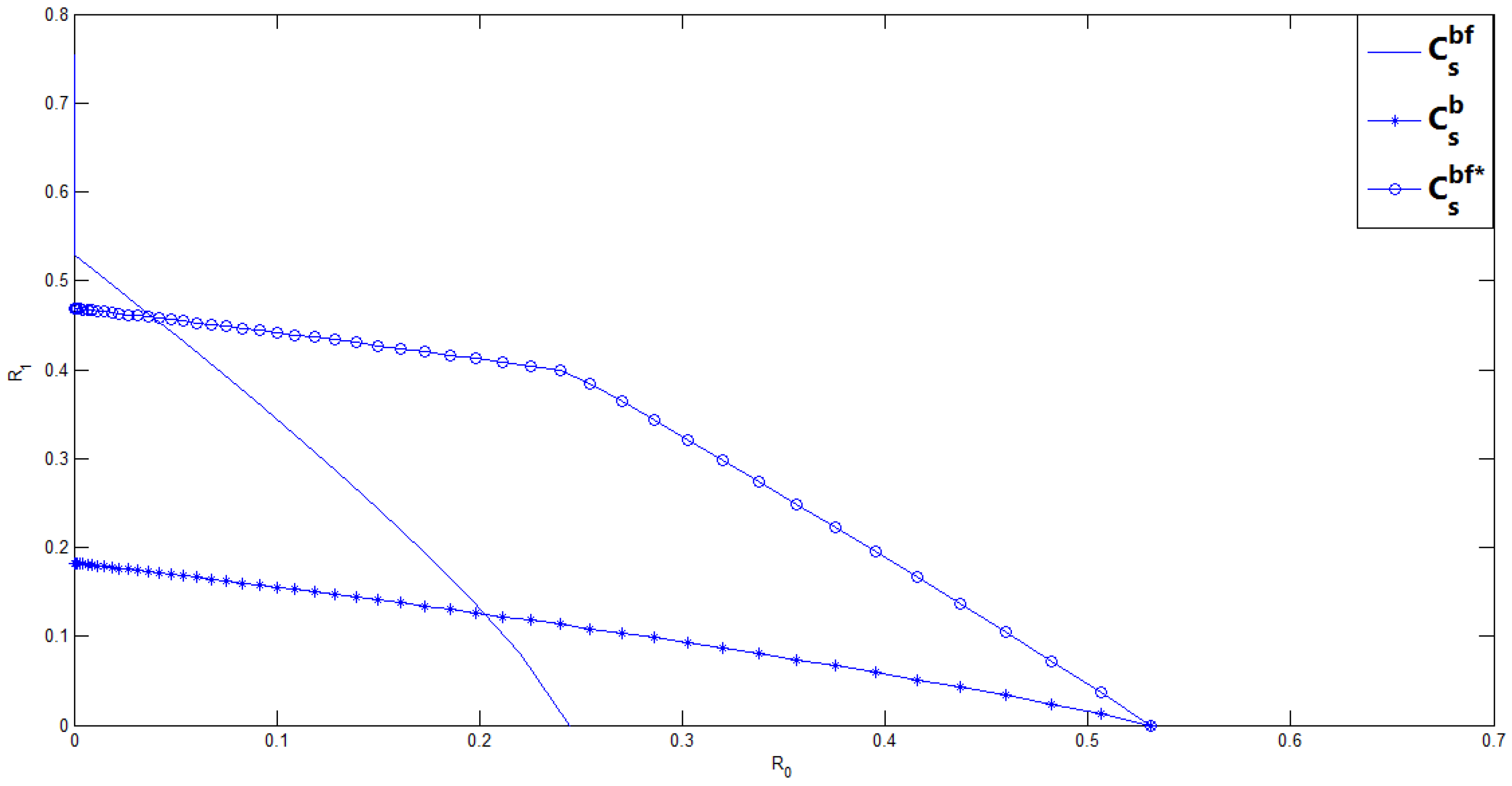
• Comparing our new inner bound $C_s^{f-new}$ with the previous Ahlswede and Cai’s inner bound ${\mathcal{C}}_s^{f-cai}$, in general, we do not know which one is larger. In the next section, we consider a binary case of the BC-CM with noiseless feedback, and compute these inner bounds for this binary case. From this binary example, we show that the maximum achievable $R_1$ (the transmission rate of the confidential message with perfect secrecy constraint) in $C_s^{f-new}$ is larger than that in ${\mathcal{C}}_s^{f-cai}$, however, the enhancement of $R_1$ is at the cost of reducing the transmission rate of the common message $R_0$.
• Note here that in $C_s^{f-new}$, the auxiliary random variable U represents the encoded sequence for the common message and V represents the encoded sequence for both the common and confidential messages. The auxiliary random variable $V_0$ is both the legitimate receiver and the wiretapper’s estimation of U, and the index of $V_0$ is related to the update information generated by the noiseless feedback. The auxiliary random variable $V_1$ is the legitimate receiver’s estimation of V, and $V_2$ is the wiretapper’s estimation of V. Both the indexes of $V_1$ and $V_2$ are with respect to the update information. The inner bound $C_s^{f-new}$ is constructed by using the feedback to generate a secret key shared between the legitimate receiver and the wiretapper, and generate update information used to construct estimation of the transmitted sequences U and V. The estimation of U and V helps both the legitimate receiver and the wiretapper to improve their own received symbols Y and Z.

3. Binary Example of the BC-CM with Noiseless Feedback

Now we consider a binary case of the model of Figure 1. In this case, the channel input is X and output Y, Z takes values in $\{0,1\}$, and they satisfy

$$\begin{array}{c}Y=X+Z_1,Z=X+Z_2,\hfill \end{array}$$

(14)

where $Z_1\sim Bern\left(p\right)$ ($p<0.5$) and $Z_2\sim Bern\left(q\right)$ ($q<0.5$) are the channel noises for the transmitter-legitimate receiver’s channel and transmitter-wiretapper’s channel, respectively, and they are independent of each other and the channel input X.

Without noiseless feedback, letting $P(U=0)=\alpha$, $P(U=1)=1-\alpha$, $P(V=0)=\beta$, $P(V=1)=1-\beta$, $U+V=X$, using the fact that U is independent of V, and substituting (14) into (2), it is not difficult to calculate the secrecy capacity region ${\mathcal{C}}_s^b$ of the binary BC-CM, and it is given by

$$\begin{array}{c}{\mathcal{C}}_s^b=\{(R_0,R_1):0\le R_0\le min\{1-h(\beta \star p),1-h(\beta \star q)\}\hfill \\ 0\le R_1\le h(\beta \star p)-h\left(p\right)-h(\beta \star q)+h\left(q\right)\},\hfill \end{array}$$

(15)

where $h\left(x\right)=-xlog\left(x\right)-(1-x)log(1-x)$ and $a\star b=a+b-2ab$. Here, note that the region (15) is achieved when $\alpha =0.5$.

With noiseless feedback, first, we compute Ahlswede and Cai’s achievable secrecy rate region for this binary case. Letting $P(U=0)=\alpha$, $P(U=1)=1-\alpha$, $P(V=0)=\beta$, $P(V=1)=1-\beta$, $U+V=X$, using the fact that U is independent of V, and substituting (14) into (4), it is not difficult to calculate Ahlswede and Cai’s achievable secrecy rate region ${\mathcal{C}}_s^{bf*}$ for this binary case, and it is given by

$$\begin{array}{c}{\mathcal{C}}_s^{bf*}=\{(R_0,R_1):0\le R_0\le min\{1-h(\beta \star p),1-h(\beta \star q)\}\hfill \\ 0\le R_1\le min\{h(\beta \star p)-h\left(p\right),{[h(\beta \star p)-h\left(p\right)-h(\beta \star q)+h\left(q\right)]}^{+}+h\left(p\right)\}\},\hfill \end{array}$$

(16)

where ${[x]}^{+}=x$ if $x\ge 0$, else ${[x]}^{+}=0$. Comparing (16) with (15), it is easy to see that the noiseless feedback enhances the secrecy capacity region of the binary BC-CM. Here the region (16) is achieved when $\alpha =0.5$.

Then, it remains to compute our new achievable secrecy rate region for this binary case. Letting $V_1=(U,V)$, $V_2=U$, $V_0=Z_1$, $P(U=0)=\alpha$, $P(U=1)=1-\alpha$, $P(V=0)=\beta$, $P(V=1)=1-\beta$, $U+V=X$, using the fact that U is independent of V, and substituting (14) into $C_s^{f-new}$ of Theorem 1, it is not difficult to show that the achievable secrecy rate region ${\mathcal{C}}_s^{bf}$ of our new feedback scheme is given by

$$\begin{array}{c}{\mathcal{C}}_s^{bf}=\{(R_0,R_1):0\le R_0\le min\{1-h(\beta \star p)-h\left(p\right),1-h\left(\beta \right)-h\left(q\right)\}\hfill \\ 0\le R_1\le min\{h\left(\beta \right),h\left(\beta \right)-h(\beta \star q)+h\left(p\right)+h\left(q\right)\}\hfill \\ 0\le R_1+R_2\le min\{1-h\left(\beta \right)-h\left(p\right)-h\left(q\right),1-h(\beta \star q)-h\left(p\right)\}\}.\hfill \end{array}$$

(17)

The achievability of ${\mathcal{C}}_s^{bf}$ can be explained by the following simple block length-(n) scheme.

• First note that in the following explanation, the channel input $x^N$ for the i-th block ($1\le i\le n$) is denoted by ${\tilde{x}}_i$, and similar conventions are applied to $u^N$, $v^N$, $v_0^N$, $v_1^N$, $v_2^N$, $y^N$, $z^N$, $z_1^N$ and $z_2^N$. For each block, the transmitted message is composed of a common message, a confidential message, a dummy message and update information.
• (Encoding): In the i-th block ($2\le i\le n$), after the transmitter receives the feedback channel output ${\tilde{y}}_{i-1}$, he generates a secret key from ${\tilde{y}}_{i-1}$ and uses this key to encrypt the confidential message of the i-th block. In addition, since ${\tilde{y}}_{i-1}={\tilde{x}}_{i-1}\oplus {\tilde{z}}_{1,i-1}$, the transmitter also knows the legitimate receiver’s channel noise ${\tilde{z}}_{1,i-1}$ at the i-th block, and thus he chooses ${\tilde{v}}_{0,i}={\tilde{y}}_{i-1}\oplus {\tilde{x}}_{i-1}={\tilde{z}}_{1,i-1}$ as an estimation of ${\tilde{u}}_{i-1}$, ${\tilde{v}}_{1,i}=({\tilde{u}}_{i-1},{\tilde{v}}_{i-1})$ as the legitimate receiver’s estimation of ${\tilde{x}}_{i-1}$, and ${\tilde{v}}_{2,i}={\tilde{u}}_{i-1}$ as the wiretapper’s estimation of ${\tilde{x}}_{i-1}$. Note that ${\tilde{x}}_{i-1}={\tilde{u}}_{i-1}\oplus {\tilde{v}}_{i-1}$ and the update information is part of the indexes of ${\tilde{v}}_{0,i}$, ${\tilde{v}}_{1,i}$ and ${\tilde{v}}_{2,i}$.
• (Decoding at the legitimate receiver): The legitimate receiver does backward decoding, i.e., the decoding starts from the last block. In block n, the legitimate receiver applies Ahlswede and Cai’s decoding scheme [3] to obtain his update information for block n. Then using the channel output ${\tilde{y}}_n$ as side information, the legitimate receiver applies Wyner-Ziv’s decoding scheme [8] to obtain ${\tilde{v}}_{0,n}$ and ${\tilde{v}}_{1,n}$. Since ${\tilde{v}}_{0,n}={\tilde{z}}_{1,n-1}$, the legitimate receiver knows the legitimate receiver’s channel noise for block $n-1$, and thus he computes ${\tilde{y}}_{n-1}\oplus {\tilde{z}}_{1,n-1}$ to obtain ${\tilde{x}}_{n-1}$ and the corresponding transmitted message for block $n-1$. Repeating the above decoding scheme, the legitimate receiver obtains the entire transmitted messages (including both confidential and common messages) for all blocks, and since he also knows the secret keys, the real messages are decrypted by him.
• (Decoding at the wiretapper): The wiretapper also does backward decoding. In block n, the wiretapper receives ${\tilde{z}}_n$, and he applies Ahlswede and Cai’s decoding scheme [3] to obtain his update information for block n. Then using the channel output ${\tilde{z}}_n$ as side information, the wiretapper applies Wyner-Ziv’s decoding scheme [8] to obtain ${\tilde{v}}_{0,n}$ and ${\tilde{v}}_{2,n}$. Since ${\tilde{v}}_{2,n}={\tilde{u}}_{n-1}$, the wiretapper knows the common message for block $n-1$. Repeating the above decoding scheme, finally, the wiretapper obtains the entire common messages for all blocks.

The following Figure 2 shows the achievable secrecy rate region ${\mathcal{C}}_s^{bf}$ of our new scheme, Ahlswede and Cai’s achievable secrecy rate region ${\mathcal{C}}_s^{bf*}$ and the secrecy capacity region ${\mathcal{C}}_s^b$ of the binary BC-CM without feedback for $p=0.05$ and $q=0.01$, which implies that the wiretapper’s channel noise is smaller than the legitimate receiver’s. From Figure 2, it is easy to see that when the wiretapper’s channel noise is smaller than the legitimate receiver’s, the secrecy rate $R_1$ of the binary BC-CM without feedback is 0, which implies that perfect secrecy can not be achieved, and the secrecy rate $R_1$ is enhanced by using noiseless feedback. Moreover, we see that our new scheme performs better than Ahlswede and Cai’s in enhancing the secrecy rate $R_1$, however, we should notice that the boosting of the secrecy rate $R_1$ is at the cost of reducing the rate $R_0$ of the common message.

The following Figure 3 shows the achievable secrecy rate region ${\mathcal{C}}_s^{bf}$ of our new scheme, Ahlswede and Cai’s achievable secrecy rate region ${\mathcal{C}}_s^{bf*}$, and the secrecy capacity region ${\mathcal{C}}_s^b$ of the binary BC-CM without feedback for $p=0.05$ and $q=0.1$, which implies that the wiretapper’s channel noise is larger than the legitimate receiver’s. From Figure 3, it is easy to see that noiseless feedback enhances the secrecy rate of the BC-CM without feedback. However, we also should notice that the enhancement of the secrecy rate $R_1$ is at the cost of reducing the rate $R_0$ of the common message.

4. Conclusions

In this paper, we propose a new coding scheme for the BC-CM with noiseless feedback. From a binary example, we show that our new feedback scheme performs better than the existing feedback scheme in enhancing the secrecy level of the BC-CM. However, we should notice that this enhancement of the secrecy level is at the cost of reducing the rate of the common message.